Journal of Modern Physics
Vol.07 No.10(2016), Article ID:67602,11 pages
10.4236/jmp.2016.710107
A Basis for Causal Scattering Waves, Relativistic Diffraction in Time Functions
Salvador Godoy, Karen Villa
Depto de Física, Facultad de Ciencias, Universidad Nacional Autónoma de México, Mexico City, Mexico

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 March 2016; accepted 18 June 2016; published 22 June 2016
ABSTRACT
Relativistic diffraction in time wave functions can be used as a basis for causal scattering waves. We derive such exact wave function for a beam of Dirac and Klein-Gordon particles. The transient Dirac spinors are expressed in terms of integral defined functions which are the relativistic equivalent of the Fresnel integrals. When plotted versus time the exact relativistic densities show transient oscillations which resemble a diffraction pattern. The Dirac and Klein-Gordon time oscillations look different, hence relativistic diffraction in time depends strongly on the particle spin.
Keywords:
Diffraction in Time, Relativistic Diffraction in Time, Causal Scattering Basis, Transient Quantum Processes

1. Introduction
Similarities between optics and quantum mechanics have long been recognized. One example of this symmetry was obtained by Moshinsky [1] who addressed the following non-relativistic, quantum, 1D shutter problem. Consider a monoenergetic beam of free particles moving parallel to the x-axis. For negative times, the beam is interrupted at 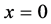 by a perfectly absorbing shutter perpendicular to the beam. Suddenly, at time
by a perfectly absorbing shutter perpendicular to the beam. Suddenly, at time , the shutter is opened, allowing for
, the shutter is opened, allowing for 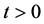 the free time-evolution of the beam of particles. What is the transient density observed at a distance x from the shutter? The shutter problem implies solving, as an initial value problem, the time-dependent Schrödinger equation with an initial condition given by
the free time-evolution of the beam of particles. What is the transient density observed at a distance x from the shutter? The shutter problem implies solving, as an initial value problem, the time-dependent Schrödinger equation with an initial condition given by
 (1)
(1)
where  denotes the step function defined as:
denotes the step function defined as:  = (1 if
= (1 if ) or (0 if
) or (0 if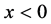 ). For
). For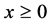 , Moshinsky proves that the free propagation of the beam has the exact solution given by:
, Moshinsky proves that the free propagation of the beam has the exact solution given by:
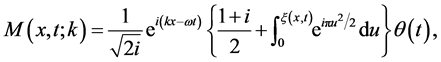 (2)
(2)
where the integral is the complex Fresnel function: 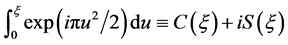 and
and 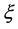 is given by
is given by
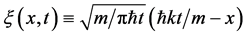 . For
. For 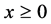 the probability density
the probability density  is then
is then
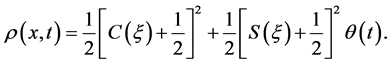
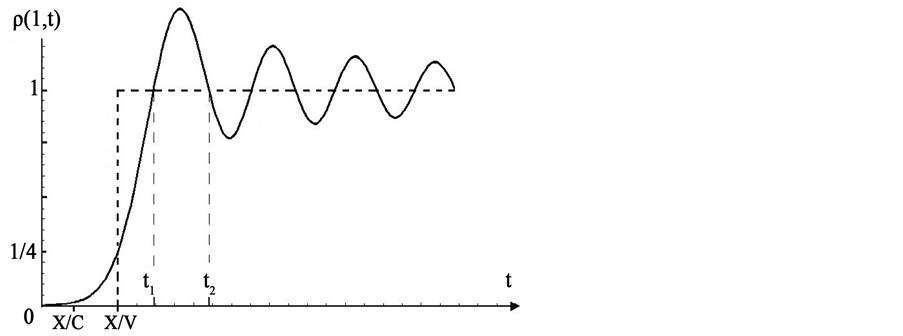
The right-hand side in Equation (3) is similar to the mathematical expression for the light intensity in the optical Fresnel diffraction by a straight edge [2] . For a fixed position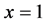
These temporal oscillations are a pure quantum phenomenon, and similar oscillations arise at the moment of closing and opening gates in nanoscopic circuits [3] . With adequate potentials added to the model, it has been used to study transient dynamics of tunneling matter waves [4] - [7] , and the transient responses to abrupt changes of the interaction potential in semiconductor structures and quantum dots [8] [9] . For a review on the subject see [10] [11] . There is, in summary, a strong motivation for a thorough understanding of transient time oscillation in beams of matter.
One of the main problems in physics is to find, for the S matrix of an interaction, restrictions which proceed from general principles such as causality [12] . Notice that there is a close relation between diffraction in times wave functions and those wave functions which are needed for a causal description. From Equation (2) we see that for 
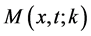
function for causal scattering. Indeed, for an arbitrary function, 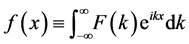
condition given by:
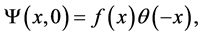
then the free time evolution of the initial condition becomes
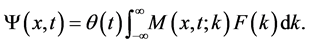
It is evident that if we want a relativistic solution for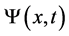
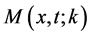
As far as we know nobody has ever reported the exact relativistic solution to the shutter problem. Moshinsky worked this problem and gave an approximated answer. In a couple of articles [13] [14] , he discussed the shutter problem using the Klein-Gordon and the Dirac equations. Using approximated solutions Moshinsky arrives to the conclusion that only for the Schrödinger equation the wave function 
Figure 1. Probability density for non-relativistic diffraction in time.
of diffraction in time in the relativistic case. In the case of photons this is obviously true, the d’Alembert’s solution does not allow such time oscillations. However, for particles with mass different from zero, in full disagreement with Moshinsky’s conclusions, we report here that relativistic diffraction in time oscillations is indeed present.
The purpose of the present paper is to derive the exact solutions for the Dirac and Klein-Gordon shutter problems. The exact transient Dirac spinors are expressed in terms of integral-defined-functions which are the relativistic equivalent of the Fresnel integrals. In partial agreement with Moshinsky’s conclusions we find that indeed the relativistic densities do not resemble the mathematical expression for intensity of light that appears in the theory of diffraction in Optics. In spite of this, when our exact relativistic densities are plotted versus time, the plots show transient oscillations which resemble a diffraction pattern. For this reason in this article we claim that impressive diffractions in time oscillations do exist in the relativistic realm. Furthermore, the Dirac and Klein-Gordon densities look quite different, which implies that relativistic diffraction in time distinguishes between spin 0 and 1/2.
2. The Dirac Shutter Problem
Consider, for relativistic particles of spin 1/2, the shutter problem. We want to find out the spinor wave function 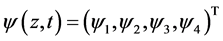
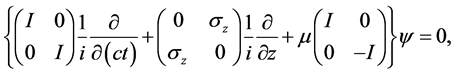
where 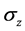
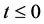
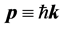
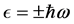
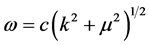
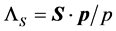
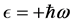
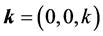
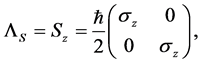
we choose the initial state with a well defined direction of spin, for instance parallel to the direction of motion,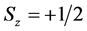
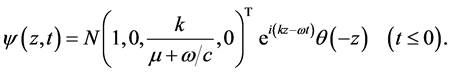
For free particles, the helicity 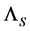
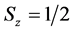
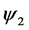
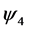
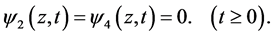
In terms of the remaining two components 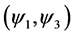
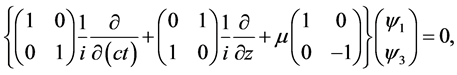
with the initial condition:
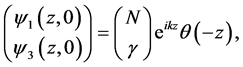
where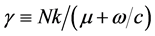
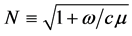
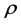
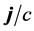
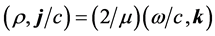
We use the Compton length 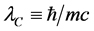

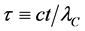
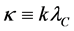
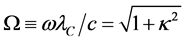
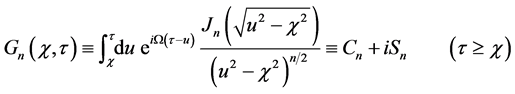
where 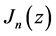

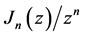
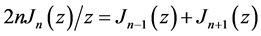
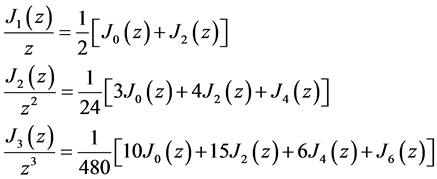
Clearly the real and imaginary parts of 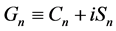
From Appendix A, for the right side of the shutter
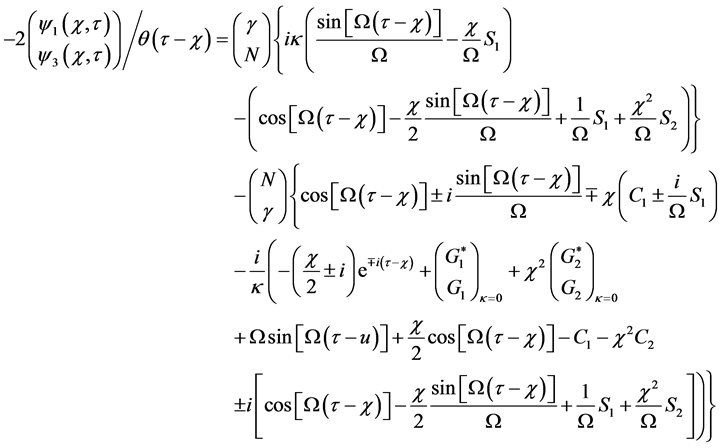
Notice the function 
3. Dirac Diffraction in Time
Given the Dirac wave function 
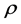
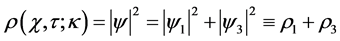
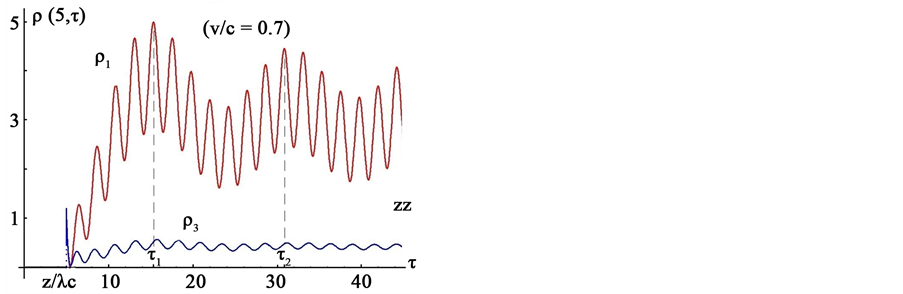
In Figure 2, for fixed values of 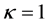
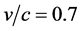
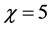
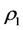
Figure 2. Dirac diffraction in time probability densities 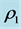
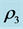
As expected, for a relativistic solution, the Dirac density vanishes for times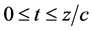
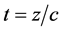
4. The Klein-Gordon Shutter Problem
For relativistic particles with spin 0, the Klein-Gordon shutter problem is, by definition, the solution 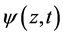
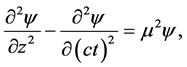
where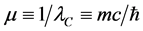
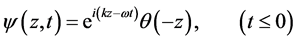
where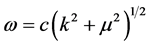
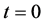
ditions:
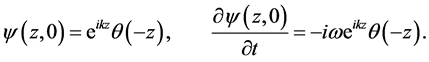
Similar to the Dirac problem, in terms of the dimensionless variables:
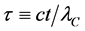
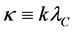
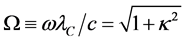
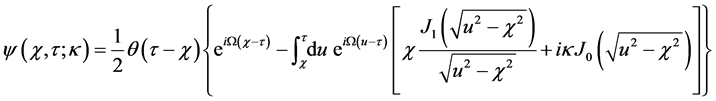
or in simplified notation
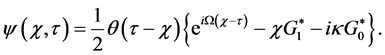
The presence of 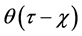
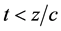
Given the Klein-Gordon wave function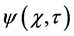
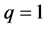
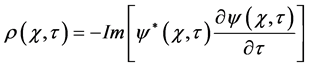
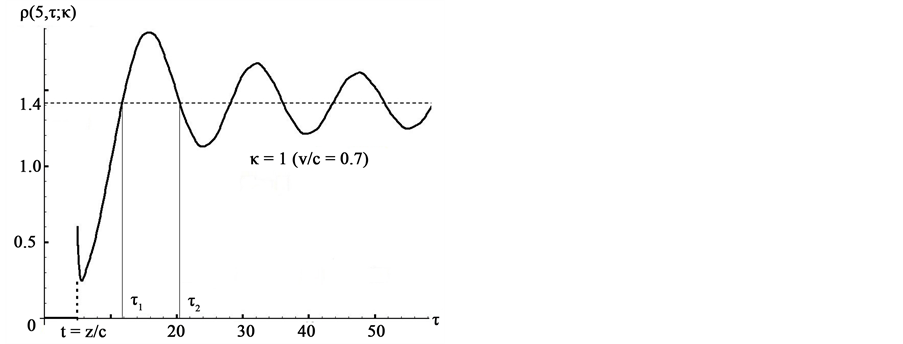
Figure 3. Typical Klein-Gordon diffraction in time for the charge density,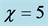
In Figure 3, for fixed values of 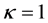
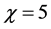
Notice that the asymptotic behavior of 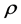
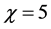
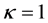
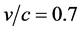
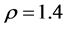
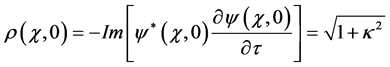
Therefore, for 
5. Conclusions
We derived the exact solutions for the Klein-Gordon and the Dirac shutter problems. In agreement with Moshinsky we find that the relativistic solutions do not resemble the analytic expression that appears in the theory of diffraction in Optics. In spite of this, we prove that when the exact Dirac and Klein-Gordon densities are plotted versus time, the following happens: 1) both densities show transient oscillations which in some way resemble the optical diffraction pattern; 2) the Dirac density looks quite different from the Klein-Gordon one, which implies that transient time oscillations depend strongly on the particle spin.
For these reasons and in total disagreement with Moshinsky’s conclusions [13] , we claim that impressive diffractions in time oscillations do exist in the relativistic realm. For spin 0 and 1/2 particles, we prove that diffraction in time oscillations exists only for particles of rest mass different from zero; photons do not show such time oscillations.
Cite this paper
Salvador Godoy,Karen Villa, (2016) A Basis for Causal Scattering Waves, Relativistic Diffraction in Time Functions. Journal of Modern Physics,07,1181-1191. doi: 10.4236/jmp.2016.710107
References
- 1. Moshinsky, M. (1951) Physical Review, 84, 525.
http://dx.doi.org/10.1103/PhysRev.84.525 - 2. Born, M. and Wolf, E. (1965) Principles of Optics. Pergamon Press, Oxford, 192-195.
- 3. Schneble, D., Hasuo, M., Anker, T., Pfau, T. and Mlynek, J. (2003) Journal of the Optical Society of America B, 20, 648-651.
http://dx.doi.org/10.1364/JOSAB.20.000648 - 4. Brouard, M. and Muga, J.G. (1996) Physical Review A, 54, 3055.
- 5. García-Calderón, G. and Rubio, G. (1997) Physical Review A, 55, 3361.
- 6. García-Calderón, G., Villavicencio, J., Delgado, F. and Muga, J.G. (2002) Physical Review A, 66, 042119.
- 7. Stevens, K.W.H. (1980) European Journal of Physics, 1, 98.
- 8. Delgado, F., Cruz, H. and Muga, J.G. (2002) Journal of Physics A: Mathematical and General, 35, 10377.
- 9. Delgado, F., Muga, J.G. and Garca-Calderón, G. (2005) Journal of Applied Physics, 97, 013705.
http://dx.doi.org/10.1063/1.1826215 - 10. García-Calderón, G., Rubio, G. and Villavicencio, J. (1999) Physical Review A, 59, 1758.
- 11. Delgado, F., Muga, J.G., Ruschhaput, A., Garca-Calderón, G. and Villavicencio, J. (2003) Physical Review A, 68, 032101.
- 12. Hilgevoord, J. (1960) Dispersion Relations and Causal Descriptions. North Holland Publishing, Amsterdam, 13-33.
- 13. Moshinsky, M. (1952) Physical Review, 88, 625.
http://dx.doi.org/10.1103/PhysRev.88.625 - 14. Moshinsky, M. (1952) Revista Mexicana de Fsica, I, 3.
- 15. Abramowitz, M. and Stegun, I.A. (1965) Handbook of Mathematical Functions. Dover Publications, New York, 1019-1030.
- 16. Duffy, D.G. (2001) Green Functions with Applications. Chapman and Hall/CRC, London, 82-84.
http://dx.doi.org/10.1201/9781420034790
Appendix A
With the help of the dimensionless variables given by:
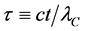
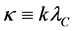
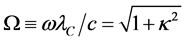
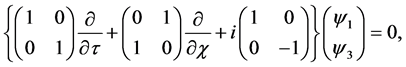
and the initial condition becomes:
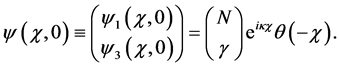
Taking the Laplace transform (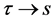
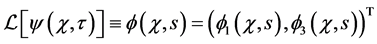
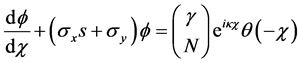
which holds in the range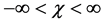
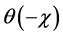
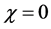
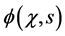
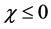
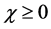
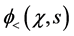
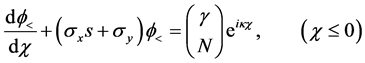
and for the right side, 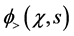
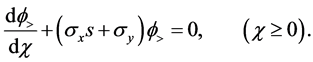
Both functions 
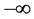
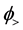
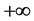
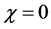
Because the matrix
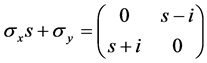
has eigenvalues given by: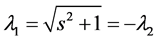
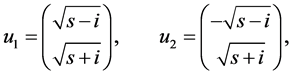
then, taking into account the boundary conditions at
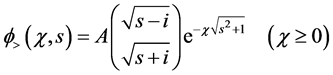
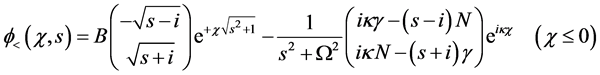
where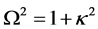
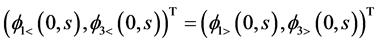
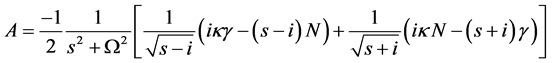
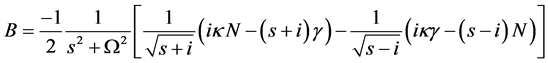
Substituting Equation (32) into Equation (30) and Equation (33) into Equation (31), we get the solution for Dirac shutter problem in the (
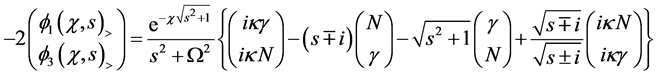
Notice the singular points at 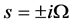
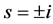
To simplify the final notation, we express the inverse Laplace transforms (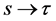
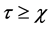
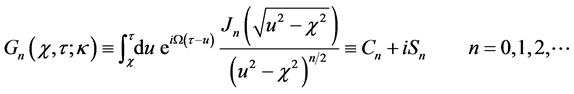
Using Laplace Transforms Tables [15] and the convolution theorem we find the following results, valid for
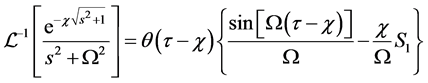
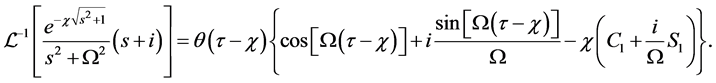
Next, we use the relation
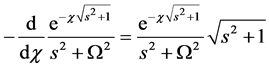
to obtain
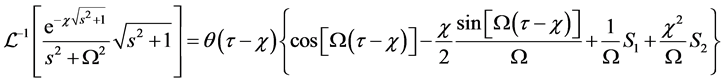
Finally, using the identities
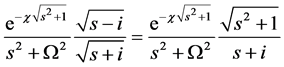
and
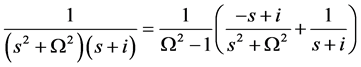
we obtain
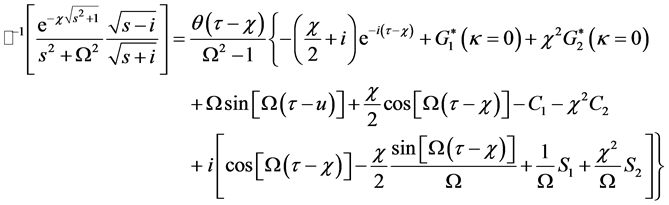
Therefore, for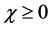
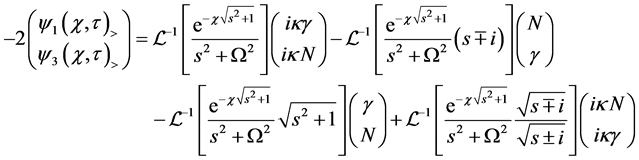
where each inverse Laplace transform has been previously calculated. We claim that Equation (43) is the exact Dirac wave function for the shutter problem, valid for 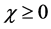
Appendix B
In a similar way to the Dirac solution, the Klein-Gordon shutter problem can be written in terms of dimen- sionless variables:
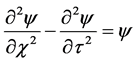
with initial conditions given by:
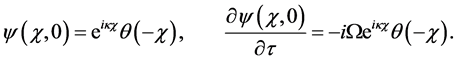
Taking the Laplace transform (
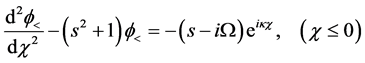
and
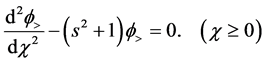
Here both functions 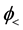
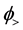
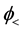
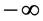
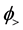
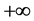
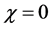
Taking into account the boundary conditions at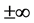
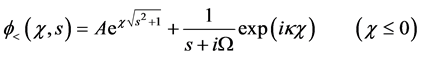
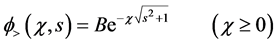
where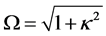
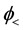
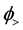
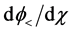
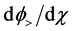
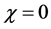
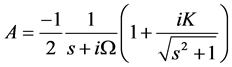
Substituting Equation (50) into Equation (48) and Equation (51) into Equation (49) we have the solutions:
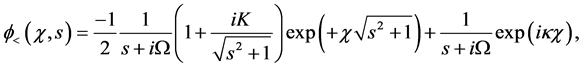
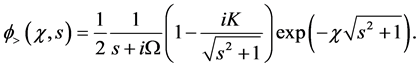
Finally, we need to invert the Laplace transforms (
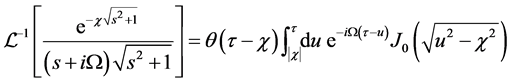
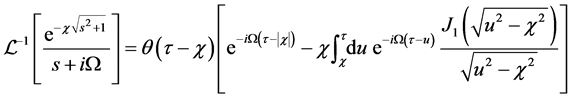
We have then the final solutions, for
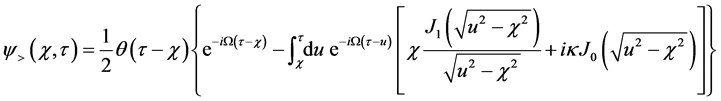
and for 
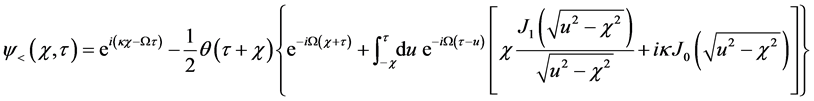
We claim that Equations (56) and (57) are the exact Klein-Gordon wave functions for the shutter problem. It’s
no surprising to find the Bessel functions 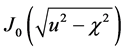
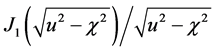
Green’s function and its derivative respectively for the Klein-Gordon equation [16] .