Journal of Modern Physics
Vol.06 No.09(2015), Article ID:59027,12 pages
10.4236/jmp.2015.69136
Dynamics of the Vacuum and Casimir Analogs to the Hydrogen Atom
Harold White*, Jerry Vera, Paul Bailey, Paul March, Tim Lawrence, Andre Sylvester, David Brady
NASA Johnson Space Center, Houston, TX, USA
Email: *harold.white-1@nasa.gov
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 July 2015; accepted 21 August 2015; published 24 August 2015
ABSTRACT
This paper will discuss the current viewpoint of the vacuum state and explore the idea of a “natural” vacuum as opposed to immutable, non-degradable vacuum. This concept will be explored for all primary quantum numbers to show consistency with observation at the level of Bohr theory. A comparison with the Casimir force per unit area will be made, and an explicit function for the spatial variation of the vacuum density around the atomic nucleus will be derived. This explicit function will be numerically modeled using the industry multi-physics tool, COMSOL, and the eigenfrequencies for the n = 1 to n = 7 states will be found and compared to expectation.
Keywords:
Vacuum, Casimir, Bohr Radius, Acoustic, Fluctuation, Fermion

1. Introduction
The current viewpoint of the quantum vacuum, or vacuum state, is that it is an immutable, non-degradable state for all observers and systems with no structure or variation. The concept of the vacuum state is typically introduced as a ground state of a harmonic oscillator, so the viewpoint that it is immutable is reasonable. How can the vacuum, being the ground state of a harmonic oscillator, be anything other than “zero” for all observers? What if, however, the vacuum could be posited to be a plenum that can be shown to be degradable, and has the capability to support particle-vacuum or particle-particle interactions that allow lower energy, ground states? It is known from experimental observation that the vacuum can exhibit characteristics that can best be associated with a degraded vacuum in the form of the Casimir force [1] -[10] . The Casimir force arises as a result of a geometric conducting boundary in the form of two plates being placed in close proximity to one another such that the geometry of the cavity can preclude the ability for certain wavelengths of light from being present in one direction. The integral of the spectrum of vacuum fluctuation frequencies between the two plates has a different starting point compared with the integral of the spectrum of vacuum fluctuation frequencies outside of the plates. The difference between these two integrals is what is considered to be responsible for the manifestation of this force. In this scenario, the vacuum state between the two plates is considered to be at a lower state than the vacuum state on the outside of the plates, or the toy vacuum model harmonic oscillator is at a lower state than the “zero” state outside of the plates. Perhaps this is illustrating a deficiency in the way in which the vacuum state is described and understood. The Casimir force strongly indicates that the vacuum is degradable; however, this concept is at odds with the idea of a zero state of a harmonic oscillator, so perhaps a prudent path to explore is to consider the concept that the quantum vacuum is a bit more “natural” than a toy harmonic oscillator and can have spatial and temporal variations, and to see if this mutable quantum vacuum identifies with any inconsistencies with observation.
2. Vacuum “Density”
The idea of a vacuum “density” expectation value will be explored by first starting with the Bohr formula that relates allowed energy levels to the primary quantum numbers. The energy for the 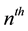 primary quantum number level of the hydrogen atom is given by the Bohr formula in Equation (1).
primary quantum number level of the hydrogen atom is given by the Bohr formula in Equation (1).
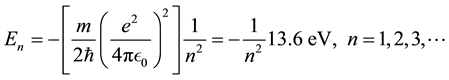 (1)
(1)
The allowed “orbit” radius for this energy level is shown in Equation (2).
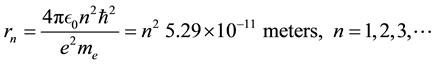 (2)
(2)
Equation (3) shows the energy relationship with the primary quantum number for the  level associated with a hydrogen-like atom with the atomic number Z.
level associated with a hydrogen-like atom with the atomic number Z.
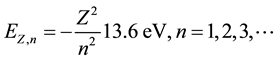 (3)
(3)
The allowed “orbit” radius for the energy level for any atom with atomic number Z is:
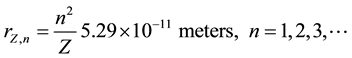 (4)
(4)
The historic perspective used in the development of the above relationships was that of the electron being in “orbit” around the nucleus in a quasi-classical sense. It is appropriate to think of these energy states as a wave function [11] , so one can calculate an average “density” of this energy state by smearing the energy over a spherical region encapsulated by the allowed radius for that state (see Equation (5)).
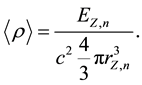 (5)
(5)
The average density for hydrogen is calculated for the n = 1 to n = 7 states in Table 1.
The question can be raised on what the calculated value for the average “density” really means―does it really indicate a perturbation (rarefication or densification) of the quantum vacuum, or is it just a number that has no physical interpretation? To help consider this question, an equation can be fitted to the radius and density data presented in Table 1 and the result is shown in Equation (6).
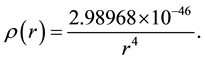 (6)
(6)
2.1. Casimir Discussion
Equation (6) shows that the density value is dependent on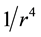 , which is a similar dependency to the Casimir force. At this point, the equation should not be viewed as a real continuous function; rather, it should be considered as a function that can only be used with the allowed, discrete values for the radius as input values. Recall that the Casimir force per unit area is (
, which is a similar dependency to the Casimir force. At this point, the equation should not be viewed as a real continuous function; rather, it should be considered as a function that can only be used with the allowed, discrete values for the radius as input values. Recall that the Casimir force per unit area is ( added for unit consistency):
added for unit consistency):
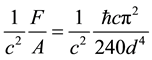 (7)
(7)
One can use Equation (7) to calculate a Casimir “density” value for the hydrogen primary quantum numbers 1 - 7 by equating the distance, d, to twice the allowed orbit radius, 2r. In a sense, the electron establishing a “boundary” at this radius could be envisioned as setting up some sort of boundary condition that mimics a Casimir cavity of sorts. These values are calculated and compared to the average density with a ratio provided in Table 2 (again Casimir force per unit area is multiplied by  for units consistency).
for units consistency).
Table 2 shows that the values will be equal if there is a factor of 1/3 added to the Casimir force per unit area ´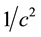 . As a short side discussion to help possibly provide an explanation for the 1/3 factor, consider the Friedmann equation:
. As a short side discussion to help possibly provide an explanation for the 1/3 factor, consider the Friedmann equation:
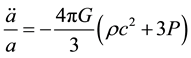
In order for there to be a universe that is accelerating as evidenced by observation, the equation of state for the vacuum, 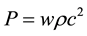 must be such that
must be such that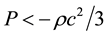 , or
, or 
Table 1. This table shows the derived “density” of a given energy state n, with Z = 1. The primary quantum number n is only varied from 1 to 7 here.
Table 2. This table compares the derived “density” of a given energy state n, with Z = 1 to the Casimir density for a cavity with a separation distance of


vacuum is just such that

The significance of this equation is that it indicates that the calculated “density” expectation value using the Bohr relationships for the energy and radius may have physical meaning as opposed to just a calculated number.
Consider the Casimir force (and Casimir equation) as it has been explored in the lab to date by numerous experimentalists with the work done by Steven Lamoreaux in 1996 establishing convincing experimental evidence of the phenomenon [2] . The Casimir force equation is used in practice to assess the force developed for a given geometry associated with a real test article that will be studied in the laboratory. When the force per unit area equation is applied to the real test article being studied in the lab, the equation provides a number that really does have physical meaning as evidenced by the real force that is measured during the study of the test article. The state of the quantum vacuum between two plates that establish a Casimir cavity is perturbed (rarified) as a result of the plates precluding certain vacuum fluctuation modes from being manifested in the cavity. The pressure inside the cavity is less than the pressure outside of the cavity.
Since the “density” using the Bohr relationships has been shown to make predictions of the energy density around the hydrogen nucleus that are identical to the modified Casimir force per unit area equation, this may indicate that these numerical values do have physical meaning and are not just a numerical calculation with no basis in nature. To be explicit, these values may indicate that the quantum vacuum around the hydrogen nucleus is not an immutable and non-degradable medium with no variation or structure, rather the vacuum appears to have a perturbation around the hydrogen nucleus that exhibits a strong dependency on
What if one considers the scenario when the atomic number Z is varied? The course is similar to the above treatment for hydrogen, except the Bohr relationships used are the equations with the Z dependency included. For this discussion, the primary quantum number n will be spanned from 1 to 7, and the atomic number Z will be spanned from 1 to 7, which corresponds to hydrogen, helium, lithium, beryllium, boron, carbon, and nitrogen respectively. The expectation value for the “density” is shown in Figure 1 for each atomic number. The observed “density” is determined using Equation (5), and the Casimir “density” is determined using Equation (9):
Figure 1. Perturbation of the Vacuum―derived “density” plotted for n = 1 to n = 7 for Z = 1 through Z = 7. The bottom line labelled Z = 1 represents hydrogen, and labels for the points representing n = 1 and n = 7 have been added. The Casimir values are also plotted as hollow circles.

A trend line has been added to each series to visually link each set of primary quantum numbers together for a given atomic number Z, and help illustrate the 

2.2. Continuous Density Function
To this point, the discussion has been about the expectation value for the “density” of the quantum vacuum for a given primary quantum number with no consideration of substructure or variation within the given spherical region. The interpretation is that the predicted “density” is an isotropic state throughout the orbital defined by the corresponding allowed radius. Since it was just shown that the expectation value for the density at each allowed orbit radius is dependent on


where the term 

The term 






A plot of this function for hydrogen is shown in Figure 2. Rather than being a series of step functions stepping down from a large value for n = 1 to a small value when n = 7 as was previously the scenario in the isotropic view, this curve is now a continuous function with slight shifts at the allowed radii which could be construed as soft boundaries between the energy levels. So rather than the density of the quantum vacuum being a uniform 


If the vacuum is indeed not an immutable and non-degradable medium, but rather a medium that can vary, as first evidenced by direct observation of the Casimir force, what can be said about what has been developed in
Figure 2. Continuous function of the vacuum perturbation for hydrogen: this function was used in the COMSOL analysis discussed in Section 2.
this discussion? A thing to note is that the integral of the perturbation of the quantum vacuum around the nucleus for a given atomic number Z and quantum number n is exactly equal to the energy level of the electron in that state. The energy level of the electron is a function of its potential energy and kinetic energy. Does this mean that the energy of the quantum vacuum integral needs to be added to the treatment of the captured electron as another potential function, or is the energy of the quantum vacuum somehow responsible for establishing the energy level of the “orbiting” electron? The only view to take that adheres to the observations would be the latter perspective, as the former perspective would make predictions that do not agree with observation. It was shown earlier that the perturbation of the vacuum around the nucleus appears to have characteristics very similar to that of the Casimir force per unit area, and since the Casimir force per unit area is negative; the integral of the vacuum perturbation would also be negative. So for n = 1, Z = 1, the energy for the captured electron is −13.6 eV, and likewise, the integral of the vacuum perturbation is −13.6 eV.
2.3. Longitudinal Vacuum Waves
If the quantum vacuum is indeed not a static immutable medium, can be locally perturbed as the above assessment indicates may be the case, and that this perturbed medium can be shown to be related to the binding energy of trapped electrons, what other characteristics might the medium have that should be considered? If the quantum vacuum is a sea of vacuum fluctuations consisting of virtual photons and virtual fermions (e.g. electron-positron pairs and others), then it may be useful to study the types of wave modes that are possible for this medium that has a 
In the acoustic case, the mode has two areas of maximum and minimum pressure separated by a region of neutral pressure that is defined by the nodal surface. In an acoustic mode, particles oscillate from the high pressure region to the low pressure region where they will reflect back again as the wave cycle oscillates. The particles are at their slowest, minimal displacements from reflection, and spend the most time in these extreme pressure regions, whereas they are at their fastest and largest displacements when they cross the nodal surface (or surfaces depending on mode). If one were to “mark” a particle that is a member of the acoustic continuum medium and try and “find” that particle or observe that particle at a particular moment in time, the odds are
Figure 3. Plot for the Z = 1, 2p orbital from orbital viewer software.
higher that the particle will be found within the high pressure lobes and lower that the particle will be found at the nodal surface. This is a classical analogy to the probability function that determines the likelihood of observing an electron (in a particular state) at some point around the nucleus.
The vacuum density function for hydrogen defined by Equation (12) and plotted in Figure 2 can be modelled and studied using the high fidelity industry tool, COMSOL Multiphysics. The vacuum medium can be modelled as a virtual plasma consisting of predominantly electron-positron ephemeral pairs. Although there will be a spectrum of other fermion-antifermion particle pairs, the dominant members of the medium at any given time will be the 

The way this equation is applied to a classical plasma is that the 




A possible source of longitudinal waves is the hydrogen nucleus. Continuing with the quasi-classical viewpoint, the electron in the n = 1 state is “orbiting” around the proton at an average distance of the Bohr radius 

Since this phase of the analysis is centered on finding the spherical acoustic modes for all of the primary quantum numbers, a 2D axisymmetric model was used. This allowed for very fine mesh size when studying the 

Table 3. This table shows the “orbital” frequency for the n = 1 to n = 7 states for hydrogen, and the sound speed. Thermal velocity is in m/s, orbital frequency is in Hz, and sound speed is in m/s.
Figure 4. Close-up of COMSOL 2D axisymmetric model.
Figure 5 shows the eigenfrequency associated with the spherical acoustic mode that falls within the n = 1 spherical region of the model. Note that the quantum vacuum density used in the COMSOL analysis is the continuous curve defined by Equation (12), and there are no “hard” boundaries in the model. The picture on the left of Figure 5 is the view from the outer extents of the model, and the picture on the right is a close-up of the mode with a cutaway depicting the intensity distribution of the mode.
This analysis result shows that this eigenfrequency is



Figure 6 shows the expanded view of the COMSOL 2D axisymmetric model used for finding eigenfrequencies. The model mesh sizing is provided to the right of the model picture, and the dense mesh sizing is apparent as the elements become unresolvable at the resolution of the figure below the primary quantum number, n = 6.
Table 4 presents the longitudinal mode eigenfrequencies for the n = 1 to n = 7 orbitals. For each row, the expected value is listed in the left column, and the COMSOL eigenfrequency value is provided to the right along with a % error. For a primary quantum number, the expected value is the frequency that the proton would oscillate about the system center of mass that consists of the proton and the orbiting electron. Figure 7 shows the eigenfrequency solution plots that correspond to those recorded in Table 4.
3. Conclusions
This paper has explored the idea of the quantum vacuum not being an absolute immutable and non-degradable state, and studied the ramifications of the quantum vacuum being able to support non-trivial spatial variations in “density”. These considerations showed no predictions that were contrary to observation, and in fact duplicated predictions for energy states associated with the primary quantum number. An explicit function of vacuum density spatial variation was derived such that it also predicted correct energy levels for the primary quantum numbers, and provided a simple acoustic model that could be numerically studied using the multi-physics software tool, COMSOL. This study showed that the quantum vacuum can support longitudinal wave modes with mode

Figure 5. COMSOL analysis results for n = 1 eigenfrequency: panel (a) shows the model out to the n = 6 orbital, and panel (b) shows a close-up view of the n = 1 solution.
Figure 6. COMSOL 2D axisymmetric model: element sizes for n = 1 to n = 7 is 1 pm, 2.5 pm, 5 pm, 10 pm, 25 pm, 50 pm, and 50 pm respectively. In this figure, the mesh size is too dense to be discernable for n = 5 and lower. Figure 3 shows the mesh for the n = 1 and n = 2 regions.
Table 4. This table shows the predicted “orbital” frequency and the COMSOL analysis eigenfrequencies for the n = 1 to n = 7 states for hydrogen. Orbital and COMSOL frequency values are in Hz.
shapes and frequencies commensurate with proton oscillation about the center of mass of the electron-proton “rotating” system associated with the primary quantum numbers. The spin-orbit coupling mode shapes associated with the p, d, and f orbital shapes are also viable acoustic wave mode solutions, and will be non-degenerate with slightly different frequencies, and hence, energies. It is a matter of future work to fully explore the p, d, and f orbital mode shapes using the explicit vacuum density function with a 3D model of sufficient resolution. The 2D approach was used for computational speed while maintaining fine mesh size. Some examples of the COMSOL results from a 3D model of a classical spherical resonance system with isotropic air medium are shown in Figure 8. In the process of searching for the n = 1 to n = 7 primary quantum number eigenfrequencies
Figure 7. COMSOL analysis results of the acoustic “natural” vacuum model The orbital shells (dark lines) can be counted, but the n = 1 radius is quite small as seen from the top left thumbnail that depicts the COMSOL eigenfrequency solution for that orbital.
Figure 8. Acoustic eigenmodes for air in a 9-in diameter spherical isotropic air cavity with soft wall boundary. A detailed analysis and experiment measuring acoustic frequencies of a ringing basketball was performed and documented in [18] .
using the 2D COMSOL model, some solutions mapped to the non-spherical, but axisymmetric electron orbitals from the p, d, and f families. Three examples are provided in Figure 9. These results suggest that the analytical methods used in this paper that were successful at the Bohr level, can be expanded to yield solutions that exhibit the full wave characteristics of QED associated with the Schrödinger wave equation:
Figure 9. 2D Axisymmetric model results that capture axisymmetric acoustic solutions like 2p, 3d, and 4f orbitals (m = 0).
There are a number of approaches detailed in the literature that seek to develop different interpretations or understandings of the origin of the wave equation, and we will only touch on few of the concepts in closing. The orthodox view is of course the Copenhagen interpretation which, in short, does not seek to assign any classical nature to the wave equation by itself, and rather only considers the wave’s statistical impact on configuration space [19] . The de Broglie-Bohm theory [20] posits the existence of a guiding global wave equation (known as the pilot wave) in a purely classical world and probabilistic quantum nature only arises as a consequence of the influence of this pilot wave on the classical world. Stochastic interpretations can be viewed as essentially fully classical interpretations of the wave equation that arises as a result of interaction with a pervasive classical zero-point radiation field (vacuum fluctuations) [21] [22] . Most recently, a paper was put forth that articulates another formulation in the debate known as a Many Interacting Worlds [23] formulation. In the MIW view, the world we live in is completely classical, but the equations of motion include a repulsive quantum force term that originates as a result of the interaction between N number of classical worlds that are close in configuration space (N can be finite or infinite), and the wave equation is an emergent characteristic in the limit of this fully mechanical theory. In our approach discussed in this paper, the ground state of the quantum vacuum has been shown to possibly exhibit structure and spatial variation that depends on the boundary conditions present, and this dynamic variation can be successfully modelled in a quasi-classical (if not fully classical) sense with COMSOL. Indeed, the wave nature of the electron orbitals within the hydrogen atom possibly has a quantum vacuum longitudinal wave mode origin explanation.
The paper will close with the following thought experiment: if the vacuum around the nucleus can be considered more of a “natural” vacuum as opposed to an immutable ground state with absolutely no spatial variation, and if there are ephemeral fermion/antifermion pairs dominated by electron-positron pairs that create and annihilate with a density that increases significantly as one moves closer to the nucleus, what is so special about the orbiting electron that allows it to be a “real” electron out of this vacuum soup? Perhaps it is not a case of uniqueness, but a case of non-uniqueness. Consider the following: a room full of paired square dancers progresses through the dance moves smoothly as called by the caller, and they occasionally change partners when instructed. What if there was an additional solitary dance partner of a given gender introduced to the ranks of this evenly matched group? And the rule is established that when a trade call is issued, the free dancer will couple to the nearest available dance partner of the opposite gender, and the previously paired dancer that misses out is now the free dancer until the next trade call is issued. As the evening progresses, nearly every dance partner of the gender that had the extra dancer has had a period when they were the “unique” solitary dancer. In an analogous way, perhaps the “real” electron is also “unique”. In one instance, the “real” electron collides with a positron vacuum fluctuation elevating the now un-paired electron vacuum fluctuation to the “real” state. This real electron continues in its real state for a brief period until it too collides with a positron vacuum fluctuation, elevating the next un-paired electron vacuum fluctuation to the “real” state. This process continues ad infinitum, and the “real” electron is not unique, and rather it is non-unique in that the “real” descriptor is associated with the state, not the individual electron. So if the “real” electron is simply a unique state of the underlying natural vacuum, an unmatched dance partner in the sea of dancers, then the probability wave functions for the electron states may be a dual representation of the longitudinal acoustic wave modes that arise as a result of the dynamics of this natural vacuum.
Acknowledgements
The primary author would like to thank the Eagleworks team for their support and hearty/heated discussions about the concepts discussed and explored in this paper. The team would like to thank the National Aeronautics and Space Administration for organizational and institutional support in the exploration and analysis of the physics in this paper.
Cite this paper
HaroldWhite,JerryVera,PaulBailey,PaulMarch,TimLawrence,AndreSylvester,DavidBrady, (2015) Dynamics of the Vacuum and Casimir Analogs to the Hydrogen Atom. Journal of Modern Physics,06,1308-1320. doi: 10.4236/jmp.2015.69136
References
- 1. Casimir, H.B.G. (1948) Proceedings of the Royal Netherlands Academy of Arts and Sciences, 51, 793.
- 2. Lamoreaux, S.K. (1997) Physical Review Letters, 78, 5.
http://dx.doi.org/10.1103/PhysRevLett.78.5 - 3. Milonni, P.W. (1994) The Quantum Vacuum: An Introduction to Quantum Electrodynamics. Academic Press, San Diego.
- 4. Milonni, P.W., Cook, R.J. and Goggin, M.E. (1988) Physical Review A, 38, 1621.
http://dx.doi.org/10.1103/PhysRevA.38.1621 - 5. Milton, K.A. (1999) The Casimir Effect: Physical Manifestations of Zero Point Energy. Invited Lectures, 17th Symposium on Theoretical Physics, Seoul National University, Korea, 29 June-1 July 1998. arXiv:hep-th/9901011 [hep-th]
- 6. Mohideen, U. and Roy, A. (1998) Physical Review Letters, 81, 4549.
http://dx.doi.org/10.1103/PhysRevLett.81.4549 - 7. Klimchitskaya, G.L., Roy, A., Mohideen, U. and Mostepanenko, V.M. (1999) Physical Review A, 60, 3487.
http://dx.doi.org/10.1103/PhysRevA.60.3487 - 8. Bressi, G., Carugno, G., Onofrio, R. and Ruoso, G. (2002) Physical Review Letters, 88, Article ID: 041804.
http://dx.doi.org/10.1103/PhysRevLett.88.041804 - 9. Chen, F., Mohideen, U., Klimchitskaya, G.L. and Mostepanenko, V.M. (2002) Physical Review Letters, 88, Article ID: 101801.
http://dx.doi.org/10.1103/PhysRevLett.88.101801 - 10. Chen, F., Klimchitskaya, G.L., Mohideen, U. and Mostepanenko, V.M. (2004) Physical Review A, 69, Article ID: 022117.
http://dx.doi.org/10.1103/PhysRevA.69.022117 - 11. Schrödinger, E. (1926) Physical Review, 28, 1049-1070.
http://dx.doi.org/10.1103/PhysRev.28.1049 - 12. Peacock, J.A. (1998) Cosmological Physics. Cambridge University Press, Cambridge, 37, 325.
- 13. Puthoff, H.E. (1987) Physical Review D, 35, 3266-3299.
http://dx.doi.org/10.1103/PhysRevD.35.3266 - 14. N.I. of Standards and Technology (2012) Codata Internationally Recommended Values of the Fundamental Physical Constants. http://physics.nist.gov/cuu/Constants/
- 15. Manthey, D. (2001) Orbital Viewer.
http://www.orbitals.com/orb/ov.htm - 16. Chen, F. (1984) Introduction to Plasma Physics and Controlled Fusion, Volume 1: Plasma Physics. Plenum Press, New York, 98.
- 17. Urban, M., Couchot, F., Sarazin, X. and Djannati-Atai, A. (2013) The European Physical Journal D, 67, 58.
http://dx.doi.org/10.1140/epjd/e2013-30578-7 - 18. Russell, D.A. (2010) American Journal of Physics, 78, 549.
http://dx.doi.org/10.1119/1.3290176 - 19. Cramer, J.G. (1986) Reviews of Modern Physics, 58, 647-687.
http://dx.doi.org/10.1103/RevModPhys.58.647 - 20. Bohm, D. (1952) Physical Review, 85, 166-179.
http://dx.doi.org/10.1103/PhysRev.85.166 - 21. Nelson, E. (1966) Physical Review, 150, 1079-1085.
http://dx.doi.org/10.1103/PhysRev.150.1079 - 22. Boyer, T.H. (1975) Physical Review D, 11, 790-808.
http://dx.doi.org/10.1103/PhysRevD.11.790 - 23. Hall, M.J.W., Deckert, D.A. and Wiseman, H.M. (2014) Physical Review X, 4, Article ID: 041013.
http://dx.doi.org/10.1103/PhysRevX.4.041013
NOTES
*Corresponding author.













