Received 27 April 2015; accepted 27 June 2015; published 30 June 2015

ABSTRACT

It is shown that a single-particle wave function Ψ, obtained (Landau, 1930) as a solution of the Schrödinger equation (for a charged particle in a homogeneous magnetic field), and an operator relation of 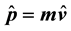(or equation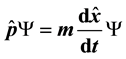) lead to the dynamic description of one-dimen- sional many-particle quantum filamentary states. Thus, one can overcome the problem, connected with the finding of many-body wave function as solution of the Schrödinger equation with a very tangled Hamiltonian for multi-body system. An effect of nonlocality appears. The dependence of the linear density of particles on the magnetic field and on the number of particles in the one- dimension filamentary multiparticle quantum structure is calculated.

Keywords:

Quantum Mechanics, Trajectory of Quantum Ensemble, Quantum Turning Points, Many-Particle Filamentary States, Magnetic Field, Effect of Nonlocality, Linear Density of Particles

1. Introduction

There is a set of interesting questions which have no clear answers. Why is our world not the continuous medium of particles? Why are there infinitely great variety of structures? The micro structures are the corner- stones of all macro structures. At the same time, the micro structures are described by quantum theory. There- fore, it would be interesting to find the answer to a question: what is the cause for arising of the quantum struc- tures? Why are ones of them stable, whereas others exist during only very short time interval? Here, we try to find the beginning of the answer to these questions.

Our attempt will be done for a particular case. The subject of our investigation is the motion of charged particles in a spatially homogeneous magnetic field. In the non-relativistic quantum mechanics, the Schrödinger equation for a particle in the homogeneous magnetic field was decided long ago (Landau, 1930), and the wave function and the energy spectrum were obtained [1] . In [1] , it is shown also that an energy of the particle is quantized only in the plane transverse to the B vector (, ,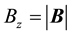) of the external homogeneous magnetic field (whereas along the magnetic field (z axis) and along the x axis, the momentum projections of particle can be varied continuously). In [1] , the wave function 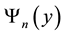for description of the motion along the line (axis y) in this 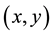plane coincides with the wave function of a linear oscillator with quantum number of n. We use these theoretical results [1] . For our investigation, it is also extremely important to interpret the wave function strictly within the theory of statistical quantum ensembles [2] . Below, in Section 2, it is discussed in detail and allows us to consider the concept of motion of statistical quantum ensemble. In Sections 3-4, for dynamical description of its motion in the plane transverse to the vector of the external homogeneous magnetic field we propose to use the well-known relation between the operators of the

momentum, velocity, coordinate, mass, and time [2] . This operator relation leads to an equ- ation. The solutions of this equation present the greatest interest. These solutions are obtained and discussed in Sections 4-5.

Obtained trajectories (dependence of coordinates on time) have a probabilistic nature (because of the pro- babilistic nature of the wave function). However, namely theirs geometry is most informative and important for applications. In Section 4, it is shown that every trajectory is one-dimensional trajectory which represents a sequence of segments at the ends of which there are quantum turning points [3] arising in the solution of the

proposed equation,. Number of segments coincides with the quantum number n of the wave

function 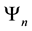(see Figure 1).

In the classical turning point, the velocity of electron is equal to zero, that is, in the turning

point the sign of velocity is changed on the opposite one [4] . Thus, the quantum turning points at the ends of every segment create the conditions for confinement of charged particle, oscillating within the segment between these two turning points. Electrons obey the Fermi-Dirac statistics. All this creates conditions for mutual isolation of segments and the possibility of filling them with particles according to the principle: one segment contains one particle or contains no particles. Each wave function corresponds to the fixed energy [1] and to the number of n of segments, isolated from one another (Section 4). Each isolated segment can be filled with one fermion (electron), that is, the number of electrons filling these segments varies from 1 to n. The collection of all these segments corresponds to a single trajectory, described by a wave function, corre- sponding to the fixed energy, which thus is shared between the indistinguishable electrons. Therefore the energy per electron decreases with increasing of the number of electrons (from 1 to n). Thus for each electron, in terms of energy it is most favourable to be in one segment and to oscillate between two quantum turning points, if all other segments already have been filled with electrons.

So in our scheme, in the plane transverse to the external homogeneous magnetic field (, ,) one can look for the linear quantum structures, the appearance of which in terms of energy is favourable for the charged fermions (electrons).

The conditions for the motion of the center (the point or in Figure 1) of linear quantum structure in the plane transverse to homogeneous magnetic field are the conditions for the motion of the center of linear quantum oscillator in plane transverse to homogeneous magnetic field. These conditions have been obtained by Landau in 1930 [1] and discussed here in Section 5.

It would be incorrect to apply the concept of a quantum ensemble for a group of interacting theoretical electrons, where each electron would have its own individual wave function. In order to avoid this mis- understanding, in Section 2 (according to [2] ), we recall the notion of quantum statistical ensemble and discuss an application to our quantum systems. In our approach, the electrons are indistinguishable. Their trajectories are

given by the wave function of harmonic oscillator, which is used in the equation, the

solution of which is a trajectory consisting of the n isolated segments (see Figure 1). These trajectories are obtained from the wave function and therefore have a probabilistic nature. We follow M. Born and A. Einstein [5] , who believe that we are hardly ever able to describe the motion of a single real physical electron, but we are able to describe the motion of a quantum statistical ensemble [5] . That is what we are trying to do in our investigation.

2. Wave Function

In the experiment, we have a real particle, however in the quantum theory we can deal only with the statistical quantum ensemble. The quantum mechanics, formulated on the principles of the quantum ensembles, is des- cribed in [2] , where the theoretical quantum ensemble is created by repetition of one process: one micro system (from an infinite set of absolutely indistinguishable micro systems) is put into one macro system (from an in- finite set of absolutely indistinguishable macro systems), which dictates condition for micro system in a quan- tum mechanical sense. All of these quantum states, obtained by this method, are named as quantum (statistical) ensemble which is described by one wave function, which, thereby, has a profound statistical nature. This determination corresponds to M.Born’s and A.Einstein’s point of view, who interpret the wave function within the statistical theory: “In any sense, the wave function does not describe the state of one separated system. The wave function describes several systems, i.e. an ensemble of the systems” [5] . Thus, if we use the wave function to obtain the trajectory, this trajectory can have only a statistical nature and, in any case, can not describe the motion of one physical particle. This is trajectory of a statistical quantum ensemble.

3. Trajectories of Statistical Quantum Ensemble

To obtain the trajectory of a quantum ensemble, we use [6] well known relation between the standard quantum operators [2]

(1)

Here, , , are operators of momentum, velocity, coordinates; and t are the particle mass and time.

The wave function describes ensemble of statistical systems [2] , for which by following (1) we can write an equation

(2)

For carrying out the mathematical calculations, we can choose the operator of coordinate in a complex form where y is real coordinate, is a complex phase [7] , and, after completion of the calcul- ations, to return to area of real numbers, we put [7] . Therefore, we choose the operator of coordinate.

This operator and the operator of momentum should be inserted into (2)

(3)

or

(4)

In [6] , for calculation of a trajectory, the other equation is used, namely it is. There- fore, our trajectories and physical results do not appear in [6] ; but, it is necessary to emphasize, that, in [6] , the base principles for an idea for movement of a quantum statistical ensemble on a quantum trajectory are for- mulated. Unlike [8] , our number of trajectories is limited by the quantum numbers.

For calculation of a trajectory for movement of the linear quantum oscillator, it is necessary to insert its wave function into Equation (4); here n is a number of quantum level.

4. Application of the Method. The Linear Quantum Oscillator

4.1. The Linear Quantum Oscillator with n = 0

For arbitrary value of n, the wave function of linear oscillator is [1] [2]

(5)

where,.

For the function is [1] [2] . Therefore for the differential equation (4) becomes

(6)

where is eigenfrequency of oscillator. To determine the integral dependence of y coordinate on time t we should take a definite integral between two points (and) of quantum trajectory [6] :

(7)

According to [9] , the integrable function should has finite value in any point lying between the points and. Therefore, the point should not be within the interval of integration. Otherwise, the infinity arises in the equation. Therefore, if the point lies outside the interval of integration, we obtain

(8)

Let us determine the complex variables and. According to the rules of complex

variables [7] , an Equation (8) can be rewritten as or, that is

(9)

An equality of real parts of Equation (9) gives equation¹

(10)

Thus, the movement of a quantum oscillator with a quantum number of between the points and occurs under the harmonic law (10). Let us emphasize, that the point is a turning point [3] [4] , where the velocity equals, that is, in this point the velocity changes its direction on the opposite one. Therefore, a quantum statistical ensemble can be only in one of two areas, that is, in the area of or in the area of, which have infinite lengths. Therefore for realisation of this quantum state it is necessary to have unlimited area of space. This condition, seems, can put some restriction on realisation of states with in the real physical sample² with its finite size on the plane, and so, they will not be con- sidered here.

The result (10) can also be expressed in the variables which are used by authors [1] [2]

(11)

For example, for these variables and, the wave function takes more convenient form

.

4.2. The Linear Quantum Oscillator with n = 1

At the trajectory calculation, we will follow an algorithm described in Section 3, use the substitution (11) which facilitates the mathematical calculations. In this case, according to (11), we should name as a coordinate along a trajectory.

For n = 1 the function (5) is. Therefore, for the differential Equation (4) is

(12)

After integration of (12) between the points and of the trajectory we obtain [10]

(13)

The real part of secondary equation in (13) is³

(14)

From (12)-(14), we should see that ξ = ±1 are coordinates of two turning points (where the velocity), which form the segment where a quantum statistical ensemble can be trapped (see Figure 1). Therefore, for the linear quantum oscillator with a quantum number of (see Figure 1), the function on

the coordinate oscillates (see (14)) within the interval.

4.3. The Linear Quantum Oscillator with n = 2

For the function (5) is. Therefore, for, the differential Equation (4) is

(15)

or

(16)

After integration of (16) between the points and of the trajectory we obtain [10]

(17)

From the left-hand equality in (17), we obtain

(18)

The real part of (18) is⁴

(19)

From (16)-(19), we should see that the points and are three turning points (where the velocity), which form two segments, isolated from one another. In each of them a quantum statistical ensemble can be trapped (see Figure 1).

There is approximation. Therefore, for the linear quantum oscillator with a quantum number (see Figure 1), the function on the coordinate oscillates (see (19)), if the vari-

able is changing within only one of two intervals: or.

4.4. The Linear Quantum Oscillator with n = 3

For, the differential Equation (4) is

(20)

or

(21)

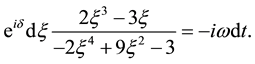
After integration of (21) between the points and of trajectory we obtain [10]

(22)

where

(23)

From (22), we have

(24)

The real part of (24) is⁵

(25)

From (21)-(23), we should see that the points are four turning points (where the velocity), and so trajectory has three segments, isolated from one another. In each of them, a quantum statistical ensemble can be trapped (see Figure 1).

There are approximations. Therefore, for the linear quantum oscillator with a quantum number of (see Figure 1), the function on the coordinate

oscillates (see (25)), if the variable is changing within only one of three intervals: or, or.

4.5. The Linear Quantum Oscillator with n = 4

According to (5), for the differential Equation (4) is

(26)

or

(27)

After integration of (27) between the points and of the trajectory, we obtain

(28)

where

(29)

From (28), we obtain

(30)

The real part of (30) is

(31)

From (27)-(29), we should see that the points and are five turning points (where the velocity), and so trajectory has four segments, isolated from one another. In each of them, a quantum statistical ensemble can be trapped (see Figure 1).

There are approximations. Therefore, for the linear quantum oscillator with a quantum number of (see Figure 1), the function on the coordinate

oscillates (see (31)), if the variable is changing within only one of four intervals: or, or, or.

5. Multiparticle Oscillator

5.1. Is Filamentary Structure the “Condensate”?

In Section 4, it is shown that a trajectory of one-dimensional quantum oscillator, described by wave function [1] with a quantum number of n, is a set of n segments which are isolated one from another (Figure 1), that is, a quantum turning points at the ends of each segment create an isolation of segments one from another. In that case, two fermions (electrons) can be in these two isolated segments.

Therefore, for any constant quantum number of n, the isolated segments can be filled with electrons like it is shown in the Figure 2.

Thus, a linear quantum oscillator with quantum number of n is described by the wave function which corresponds to the energy [1] and, simultaneously, corresponds to the number of n of segments, isolated

one from another and filled with electrons. Therefore, for simplicity, we can suppose that the energy of oscillator with quantum number of n can be shared between the electrons, which fill the segments of the oscillator (see in Figure 2).

For simplicity, we have neglected the spin term in the formula for energy of linear oscillator [1] . There-

fore in Figure 2, the energy per one electron is, where m is the total number of the indistinguishable electrons, occupying segments of n-th level (in Figure 2 the value of m is changed from 1 to n) and is cyclic frequency of electron at its movement in external transverse magnetic field [1] . If

(all segments are filled), the energy per one electron is minimal, at fixed n (see in Figure 2(c), Figure 2(g), Figure 2(o)). Therefore, more n means more favourable state for electron, if all segments are filled by other electrons (see in Figure 2(c), Figure 2(g), Figure 2(o)). In that case, a trajectory of oscillator with quantum number of n begins being as some “condensate” states of n number of electrons which are isolated one from another, but being in one quantum filamentary structure, which has tendency to grow, whereas the

linear density of electrons in filamentary structure grows with growing n because of reduce of with growing n (see Figure 1, Figure 3 and Section 5.2).

5.2. The Density of Filamentary Structure

In Section 4, it is shown the number of segments, their average length⁶

(32)

and coordinates of their endpoints are strongly correlated with a quantum number of n (see Figure 1). Moreover, in Section 4 it was obtained, the value of decreases with growing n, that is, the density of filamentary structure grows with growing n. However, this result was calculated up to only.

To determine the value of for any fixed large quantum number of n, we need to solve complicated integrals (see Section 4). However, integration does not shift the points of divergence in (4). In order not to calculate these complicated integrals, we use recurrent relation for the function (5) (see [1] )

(33)

So, to find the points of divergence⁷ (the turning points) in equation (4) and then intervals, we should just find the values of, in which there is correct equality

(34)

⁶For example, and (see Section 4.5 and Figure 1).

⁷That is, the values of in which there is equality.

In (5), the functions of are the Hermite polynomials. Their magnitudes and properties are well studied in mathematics [1] . However, any mathematical calculations of for very large n represent a great technical difficulties (see Appendix A), to overcome that (hopefully) will be possible on a supercomputer. In Figure 3, there are results obtained on a personal computer using a conventional plotter. From Figure 3, one can see that the value of decreases rapidly with increasing quantum number of n.

Now we should find linear density of filamentary structure in the metric space. In external tran-

sverse magnetic field, the electron moves with the frequency of [1] . Therefore from (11) we can

get and the average width of segment already in metric space for the fixed quantum number of n

(35)

where are from Figure 1, (32), (34) or Section 4.

The value of (35) gives information concerning the average distance between two adjacent electrons (charged fermions) in filamentary structure (under the condition that every segment was already filled by electron, Figure 2(c), Figure 2(g), Figure 2(o), etc.). From (35), one can see that properties of conform to properties of (Figure 3) but strongly depend on magnetic field. In Figure 4, this dependence is

demonstrated for different n. Thus, in one-dimensional filamentary structure, the linear density grows

with growing and n (Figure 4).

5.3. The Movement of Filamentary Structure

The motion inside the one-dimensional filamentary structures has been calculated in Section 4. To describe the

motion of filamentary structure as a whole, we will follow [1] and use the coordinate of its center as

(see coordinate or in Figure 1, Figure 2), which simultaneously is coordinate of the centre of linear quantum oscillator (see [1] ). The coordinate is constanta, if does not change, that is, there is not any accelerating field along the x-axis. However, if constant electric field is present along the x-axis, the values of and will be changing. That is the motion in so-called crossed fields (electric and magnetic). However, electrons of filamentary structure are indistinguishable, that is, their quantum motion can not be cal- culated as it was done for classical electrons [11] .

6. Conclusions

To obtain more information concerning the quantum objects, we offer to use well-known relation between the

operators of the momentum, velocity, coordinate, mass and time [2] , which leads to an equ- ation, where is wave function of a quantum system which we attempt to investigate. A

wave function has to be treated only within the theory of quantum statistical ensembles (see [2] and Section 2). Therefore, solutions of this equation are the one-dimension trajectories of a quantum ensemble, described by the function in the metric space. These trajectories have a probabilistic character because they are obtained from the function (Sections 1, 2).

If a wave function has an oscillating form (as it is for the wave function of a harmonic oscillator at), the coordinates of its minimal and maximal values are the quantum turning points⁸ [3] which divide the particle trajectory into the number of n segments (Figure 1), isolated from each other. Therefore, Fermi-Dirac statistics allows to occupy these isolate segments by electrons on the principle: every segment has one or zero number of electrons. A quantum structure arises.

In [1] , it is shown that in the plane transverse to the external magnetic field, only along the y axis, there is quantization, that is, the linear quantum oscillator states occur. In our approach, this leads to formation of one-dimensional filamentary quantum structure, which can be created by any fermions.

The movement of one-dimensional filamentary quantum structure (in the crossed electric and magnetic fields) is discussed in Section 5.

The energy of oscillator is shared between electrons which form one-dimensional filamentary quantum struc- ture. Therefore, it seems interesting to investigate the possible correlations between the oscillations of energy per one electron (in Figure 2) and the number (or density) of particles and the external magnetic field (Equation (35) and Figures 2-4).

The dependence of average distance between the particles (of one-dimensional filamentary quantum structure) on the external transverse magnetic field and on the number of particles (provided that all segments are occupied by electrons) is calculated. It is given in Figure 4.

The dependence, presented in Figure 4, is connected with the one, given in Figure 3 (see Equation (35)). The properties of, presented in Figure 3, are determined only by the properties of the wave function (see Appendix A), that is, the dependence (of and on n), shown in Figure 3, Figure 4, is a quantum effect.

⁸where the velocity takes the value

Figure 2 shows that the quantum states, obtained in Section 4, can be filled by indistinguishable electrons. Thus, if two electrons within two segments of one incipient filamentary structure (Figure 5) are separated by big distance in metric space and oscillate (see Sections 4.1-4.5), they “know” (Section 5.1) concerning existance each other without visible interaction between them. It is like an effect of non-locality.

In Section 5.1, it is discussed that an energy per one electron of filamentary structure is reduced with growing quantum number of n (Figure 2(c), Figure 2(g), Figure 2(o), etc.), that is, filamentary structure has tendency to grow. In Section 5.2, it is shown that the density of electrons grows with growing quantum number of n, that is, with number of electrons in filamentary structure (Figure 4). These properties of filamentary structure look like a gravitational attraction.

Figure 4 gives information concerning the density of electrons in the one-dimension filamentary structure as a function of external transverse magnetic field B and of a quantum number of n (or of number of particles

in filamentary structure). However, instead of electrons, the protons or nuclei could be considered (or any composite or elementary fermions). Thus, the dependence, presented in Figure 4, can open the way to nucleosynthesis.

In Equation (35), there is no dependence of on the particle mass. This dependence occurs only for a

frequency [1] . Therefore, Figure 2 and Figure 4 could open the way to trapping of any charged

particles to manipulate with them.

Offered approximation could be applied to investigate of two-dimensional structures in magnetic field. How- ever, these structures could be formed instantly and locally in any place where there is two-dimensional movement of charged fermions in transverse homogeneous magnetic field. Change in the direction of the magnetic field leads to the collapse of one-dimensional quantum filamentary structures and to their instant formation in a new plane transverse to the new direction of the magnetic field. To the casual observer it looks like chaos (or “crazy” dance of particles) whereas, in fact, it is continuous transformation from one quantum structure to another.

Therefore, investigation of local magnetic fields in different structures could be useful for understanding the nature of appearance of structures.

The possible applications of offered approach could be found in [12] , where one-dimensional filamentary multiparticle quantum structure was named as United Quantum Oscillator (UQO).

Acknowledgements

I am grateful to V. M. Chudakov for useful discussions, K. G. Gulamov for help and V. Sh. Navotny for providing the Internet communications. My special thanks to E. N. Tikhonov for his patience and support.

References

Appendix

From Equation (4), one can see that the y (or, see (11)) coordinates of turning points are determined by an

equation which means. Therefore, the turning points are the points where

there is an extremum of the function (that is, its minimal and maximal values).

An Equation (5) shows identity of points of extremum for the and functions. One of the properties of the function is that, along the -axis, the “density” of these points of extremum grows with growing n, and we obtain the Figure 3. Thus the dependence shown in Figure 3 reflects the properties of wave function.

Equation (33) opens the way to calculate these points of extremum by an Equation (34), and then to obtain the dependence of on n for very large values of n.

The computational problem is that the numerical coefficients of function is ~10²⁰ for,

whereas it would be interesting to know the linear density of particles for the value of. It

could be useful information, related to the two-dimension electron density on the graphene surface, or connected with density of a two-dimensional plasma instability in the process of nucleosynthesis, or related with other collective phenomena.

NOTES

¹The module in the right-hand part of (9) is a result of the existence of module in the left-hand part.

²However, in our approach we do not impose any boundary condition.

³The module in a right-hand part of (14) is a result of existence of module in the left-hand part of (14).

⁴The module in a right-hand part of (19) is a result of existence of module in the left-hand part of (19), see right-hand equality in (17).

⁵The module in a right-hand part of (25) is a result of existence of module in the left-hand part of (25) (see (23)).