Journal of Modern Physics
Vol.05 No.18(2014), Article ID:52746,16 pages
10.4236/jmp.2014.518208
Experimental Validation and Simulation of Fourier and Non-Fourier Heat Transfer Equation during Laser Nano-Phototherapy of Lung Cancer Cells: An in Vitro Assay
Mohammad E. Khosroshahi1,2, Lida Ghazanfari2,3, Payam Khoshkenar4
1Center for Advanced Diffusion-Wave Technologies (CADIFT), Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, Canada
2Laser and Nanobiophotonics Laboratory, Biomaterial Group, Faculty of Biomedical Engineering, Amirkabir University of Technology, Tehran, Iran
3Max Planck Institute for the Science of Light, Erlangen, Germany
4Department of Biomedical Engineering, College of Engineering & Science, Louisiana Technology University, Ruston, USA
Email: Khosrom@mie.utoronto.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 September 2014; revised 18 October 2014; accepted 12 November 2014
ABSTRACT
This paper investigated the numerical scheme extended to solve the hyperbolic non-Fourier form of bioheat transfer equation and the experimental trials were conducted to validate the numerical simulation. MNPs were prepared via co-precipitation and modified with a silica layer. The amino modified Fe3O4/SiO2 nanoshells were covered with gold colloids producing nanoshells of Fe3O4/SiO2/Au (MNSs). In vitro assays were performed to determine the effect of apoptosis of QU-DB lung cancer cells based on the cells morphology changes. Cell damage was reduced by decreasing the power density of laser. Also, a larger area of damage on cell culture plates was observed at longer intervals of laser irradiation. The effect of nanoshell concentration and irradiation rate has been evaluated. A maximum temperature rise of 6˚C was achieved at 184 W/cm2 and concentration of 0.01 mg/ml. The experiment confirmed a hyperbolic behaviour of thermal propagation. The results revealed that the three-dimensional implementation of bioheat equation is likely to be more accurate than the two-dimensional study.
Keywords:
Bioheat Equation, Gold Nanoshells, Laser Hyperthermia, Lung Cancer Cells, Surface Plasmon Resonance

1. Introduction
The latest statistics shows that cancer remains one of the leading causes of death worldwide, accounting for 7.6 million deaths (around 13% of all deaths) in 2008 [1] . However, advances in nanotechnology have changed the very foundations of cancer diagnosis, treatment, and prevention and hence offer some exciting possibilities to keep pace with today’s advances in cancer treatment [2] - [4] . In recent years conventional surgical treatments of cancer have been rendered ineffective because these techniques are extremely invasive and usually associated with high morbidity.
Among recent technologies for cancer treatment, thermal therapies employing a variety of heat sources including ultrasound [5] , microwaves [6] [7] , radiofrequency [8] , and lasers [9] - [12] can provide a minimally invasive alternative to conventional surgical treatment of solid tumors. Technological advancements, such as small, compact, high-power laser systems with actively cooled applicators, have introduced highly promising modalities for cancer therapy, most commonly the photothermal and the photodynamic therapy [13] - [20] .
On the other hand, emergence of noble metal nanostructures with remarkable set of optical, chemical and physical properties, has regulated thermal energy into target regions delivered by optical fibres to provide a lethal dose of heat with damage to surrounding healthy tissue as little as possible [21] [22] . Gold nanoshells (GNSs) are spherical particles with diameters typically ranging in size from 10 to 200 nm and are composed of a dielectric core covered by a thin gold shell. Unique to NSs, it is their localized surface plasmon resonance (LSPR) which greatly intensifies their interaction with the electromagnetic field. The light interaction with metal induces resonance effect which arises from collective oscillations of conductive metal electrons at the nanoshell surface. This subsequently couples with the surface plasmons to create self-sustaining, propagating electromagnetic waves known as surface plasmon polaritons (SPPs).
Relative thickness of the core and shell layers of the nanoparticle (NP) has a key role in the plasmon resonance characteristic and the resultant optical absorption of nanoshells [23] - [27] . The absorption band of core-shell particles can be tuned by adjusting the ratio of the thickness of the gold shell to the diameter of the dielectric core to enable photothermal therapy in appropriate region [28] .
From a photothermal therapy perspective, the wavelength of maximal absorption and the absorption cross- section are key features to consider when selecting a particle for hyperthermia. Meanwhile, size and surface characteristics of the NP are of prime importance in the biodistribution and rapid clearance of NP from the blood which affects its delivery to target sites [21] [22] . In order to optimize the delivery of gold nanoparticles (GNPs) and enhance ablative therapy, functionalization of NPs and their surface modification with cargoes such as peptides, antibodies, and small-molecule ligands have been reported in the literature [28] - [32] . Other advantages of GNPs including biocompatibility and non-cytotoxicity have opened several additional promising research avenues for further optimization of the AuNPs-mediated photothermal therapy [33] - [35] .
Recent developments in computational modeling of thermal therapy have attempted to model the heating profile of irradiated tissue which could be essential for effective clinical translation [36] [37] . An accurate modeling and simulation of thermal distribution and temperature elevation of nanoparticle-laden tissue is important for describing the heat transfer within a tissue which would lead to an optimized thermal ablation in solid tumors. Numerous mathematical models have been proposed to gain further information on the thermal behaviour and heat-affected zone of NP-laden tissue. In most cases, the temperature distribution in the tissue was obtained using the heat transfer equation proposed by Pennes [38] . Previous studies have employed both parabolic heat transfer equation (PHTE) and hyperbolic heat transfer equation (HHTE) to model heating of biological tissues; however, many of them considered laser heating source as a generation term without dealing with plasmonic heating source. The principle goal of this report is to compare the experimental and numerical results in order to achieve a qualitative understanding of the NS-assisted laser hyperthermia, where for the simulation, the PHTE and HHTE were solved numerically using a finite element analysis.
2. Materials and Methods
2.1. Synthesis and Coating Fe3O4/SiO2 Nanoshells with Gold
Fe3O4 NPs and SiO2 coated Fe3O4 NPs were synthesized via chemical coprecipitation and Stober methods, respectively as described before [39] . Finally, the Fe3O4/SiO2 nanoparticles were coated with 2 - 3 nm gold nanoparticles to get a dark pink solution which is characteristic of nanoshell formation as suggested [40] [41] .
2.2. Preparation of Cells and Gold Coated Fe3O4/SiO2 Nanoshells Compound
QU-DB lung cancer cells (purchased from the Pasteur Institute, National Cell Bank of Iran) were seeded in 96-well tissue culture plates and incubated at 37˚C and 5% CO2. Dulbecco’s Modified Eagle Medium (DMEM- GIBCO) supplemented with 10% fetal bovine serum (FBS-GIBCO) was used as cell culture medium (CCM). Serum-free cell culture medium containing nanoparticles maintained under UV for 4 hours before adding to cell cultures. After 24 hours incubation period, cell culture medium was replaced with two different concentrations of GNs suspension including 0.01 and 0.1 mg/ml. The nanoshells used in our experiments had a diameter of ~85 nm (75 - 100 nm) with an average shell thickness of ~35 nm which was measured with transmission electron microscopy (TEM). TEM micrograph (Figure 1(a)) shows clustering of small gold NPs assembled on the surface of larger silica NPs. The AFM image in Figure 1(b), indicates some possible agglomeration causing surface rough morphology.
2.3. In Vitro Assay
The lung cancer cells were first incubated with serum free cell culture medium containing synthesized gold coated Fe3O4/SiO2 NSs for 24 hours. The cell-NP medium was then irradiated by a NIR diode laser at 800 nm ± 10 nm with focal spot of 7 mm2 to evaluate the heat induced apoptosis. Cells were divided into two treatment groups. Sever hyperthermic treatment with 184, 157, and 71 W/cm2 for one minute and mild hyperthermic treatment with 42 and 14 W/cm2 for 3 minutes. The temperature was monitored by a digital thermometer with 0.1˚C precision (CHY502A1, MULTI LOGGER) connected to laptop for further processing. The effects of hyperhtermic treatment and heat-induced apoptosis were evaluated according to alteration of cell morphology. Living QU-DB lung cancer cells have fibroblast-like morphology while damaged cells shrink and have rounded shape [42] . Cell membrane, cytoskeleton [43] , intracellular proteins [44] , nucleic acid and mitochondrial function are molecular effectors during hyperthermia and have been shown that actin filaments become insoluble during hyperthermia [45] . Studies have shown the shrinkage or morphological alterations of endothelial cells in response to heat stress which have been attributed to disaggregation of the cytoskeleton after hyperthermia [43] . This phenomenon has been supported independently in electron microscopic studies [46] . Changes in cell membrane function are generally considered as the main cause of cell death. Observation of altered membrane fluidity and permeability with increase in temperature, support this concept [45] . These phenomena may become evident during the recovery phase of the cell to the base-line temperature, but not immediately after heating [46] . Therefore, cells undergoing apoptosis shrink and exhibit cytoplasmic and chromatin condensation and in the final stages they fragment into small apoptotic bodies [47] .
Figure 2(A) illustrates normal morphology of cancer cells i.e. before treatment. To determine the effect of laser
Figure 1. (a) TEM image and (b) AFM micrographs in 3D-height of gold coated Fe3O4/SiO2 nanoshells.
Figure 2. Optical microscopy of (A) control cells (untreated tumoric cells) 24 hours after subculture and (B) the cells after laser treatment without nanoshells.
radiation on cultured cells without NPs, they were irradiated at 157 W/cm2 and as is seen in Figure 2(B) no significant change was observed in cell morphology.
By increasing the exposure time to 180 seconds at lower power densities, the damaged area was extended, and more cells at the region far from the laser beam were affected because of heat transfer. Figure 3 demonstrates the cellular morphology changes at 157 W/cm2 for one minute. As shown in Figure 3, cells in the irradiated region have a circular shape which is the characteristic of apoptotic cells [48] . The percentage of apoptosis was calculated by dividing the total number of rounded cells by the total number of cells at the focal point of the laser as well as the immediate surrounding area (6 × 104 µm2). At 184 and 157 W/cm2 and irradiation time of 60 s all the cells suffered apoptosis. But, the heat-inducted death was reduced to 92.78% at 71 W/cm2at the same period of time. The percentage of damaged cells and GNs decreases with the increase of distance from the center of the beam. In this situation, the percentage of damaged cells was reduced to 57% and 47.15% at 42 and 14 W/cm2, respectively.
This experiment was repeated three times in order to prove the observed reproducibility of the data. Furthermore, the effect of NPs concentration on cell apoptosis is shown in Figure 4 where the amount of damaged cells is reduced by decreasing the concentration to 0.01 mg/ml at 157 W/cm2 during a one minute exposure. The results indicate that the concentration of NSs had significant effects on the amount of heat generated at a given power density. For core-shell, the NP efficiency parameter has the form [49]
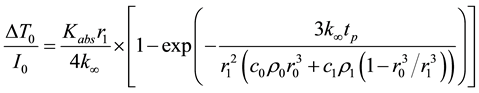 (1)
(1)
where I0 is the intensity of the laser radiation during pulse duration, tp and Kabs is the efficiency factor of absorption, k∞ is the coefficient of thermal conduction of the ambient medium, c0, ρ0 and c1, ρ1 are the heat capacity and density of the core material (Magnetite-Silica) and shell (Gold) accordingly, r0 and r1 are the radii of the core and shell and the thickness of the shell r0 = r1 − r0. The maximum value of the parameter ΔT0/I0 represents the efficiency of transformation of absorbed optical energy by NPs into thermal energy. In our case this corresponds to about 12% and 7% for CCM + MNSs at 0.1 mg/ml and 0.01 mg/ml + QU-DB lung cancer cells, respectively.
By increasing the power density, the temperature increased faster and higher. One important aspect of this finding was that the maximum temperature of 56˚C and 59°C of CCM decreased to ≈46˚C and 50˚C for 0.01 mg/ml and 0.1 mg/ml, respectively which likely is attributed to the protein adsorption in the presence of cells. Optical microscopy showed that the majority of cells have become circular due to induced thermal stress. Clearly most of the gold-coated Fe3O4/SiO2 nanoshells are accumulated at the center of the wells, where the laser beam was focused. This may be due to the movement of nanoshells in the direction of the force gradient towards the center of the beam [50] .
3. Mathematical Framework
The well-known Fourier’s law of heat conduction presents a linear relationship between the heat flux 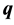 through a material and the gradient of temperature (T), whose differential form is:
through a material and the gradient of temperature (T), whose differential form is:
Figure 3. Illustration of QU-DB lung cancer cells after laser irradiation at different powers of 157 W/cm2 for 60 s at 0.1 mg/ml. Three different parts were photographed and depicted in a row: the focal point of the laser beam at the center (left), the adjacent region (middle) and far region (right). Arrow head: nanoshells colonies; arrow: dead cells.
Figure 4. Illustration of QU-DB lung cancer cells after hyperthermia treatment at 157 W/cm2 and two different concentrations of gold coated Fe3O4/SiO2 nanoshells: 0.1 mg/ml (left) and 0.01 mg/ml (right) at 60 s. More colonies and apoptotic cells can be seen in the sample with concentration of 0.1 mg/ml.
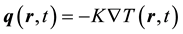 (2)
(2)
where K and  are thermal conductivity of material in W/m×K and gradient operator, respectively. The Fourier’s law is simple in mathematics and has been widely used even though it is only an empirical relationship. In principle, however, the Fourier’s law leads to an unphysical infinite heat propagation speed within a continuum field for transient heat conduction processes because of its parabolic characteristics, which is in contradiction with the theory of relativity [51] [52] . To overcome this spatio-temporal challenge especially in ultra-small scales the CV model proposed by Cattaneo and Vernotte [53] [54] :
are thermal conductivity of material in W/m×K and gradient operator, respectively. The Fourier’s law is simple in mathematics and has been widely used even though it is only an empirical relationship. In principle, however, the Fourier’s law leads to an unphysical infinite heat propagation speed within a continuum field for transient heat conduction processes because of its parabolic characteristics, which is in contradiction with the theory of relativity [51] [52] . To overcome this spatio-temporal challenge especially in ultra-small scales the CV model proposed by Cattaneo and Vernotte [53] [54] :
 (3)
(3)
where  denotes the relaxation time that tissue responds to the heat perturbation. The CV model gives rise to a wave-type of heat conduction equation, namely, hyperbolic heat conduction equation. The introduced time- derivative term in the CV model describes a wave nature of heat propagation at a finite speed, which has been proved in both theory and experiments [54] . The natural extension of this model yields a constitutive relation called the single-phase-lagging heat conduction model which is written as follow:
denotes the relaxation time that tissue responds to the heat perturbation. The CV model gives rise to a wave-type of heat conduction equation, namely, hyperbolic heat conduction equation. The introduced time- derivative term in the CV model describes a wave nature of heat propagation at a finite speed, which has been proved in both theory and experiments [54] . The natural extension of this model yields a constitutive relation called the single-phase-lagging heat conduction model which is written as follow:
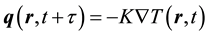 (4)
(4)
It has been further extended to the dual-phase-lagging (DPL) model by Tzou [55] , which is given as:
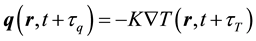 (5)
(5)
where  and
and 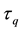 are the phase lags of the temperature gradient and the heat flux vector in second, respectively. The first order Taylor expansion of Equation (5) gives:
are the phase lags of the temperature gradient and the heat flux vector in second, respectively. The first order Taylor expansion of Equation (5) gives:
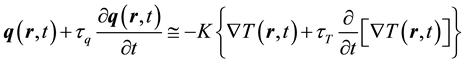 (6)
(6)
Taking the divergence of (6) and substituting  to the energy equation established at a general time t:
to the energy equation established at a general time t:

which leads to the T representation of the DPL model:

where k and 



which is also called “thermal wave speed”. For
Equation (8) is of considerable importance in the investigation of a variety of heat transfer problems. The most commonly used form of Equation (8) to solve heat transfer problems for either a biological fluid or tissue is Pennes’ (1948) bioheat equation because of its conciseness and validity. The bioheat transfer equation was first introduced by Pennes [38] to model heat transfer in perfused tissue such that:

where ρ, C, 



The blood perfusion 



where 

where PLaser (W) is laser power, 


where βr is reduced scattering coefficient (m−1) which is a lumped property incorporating the scattering coefficient β (m−1) and 

Also,

Moreover, an additional term accounts for thermal energy release by the gold nanoshells should be added to the Equation (12):

where the term in the bracket is plasmonic heating induced by exposure to laser irradiation with ε, L and c being the wavelength-dependent molar absorptivity (extinction coefficient), the distance the light travels through the material (i.e. the path length) and the concentration of absorbing species according to the Beer-Lambert’s law.
4. Thermophysical Properties of Nanoparticles
In order to analyze the modeled conditions, thermophysical properties of materials used in our experiments, were taken from literature or calculated by the formulas summarized by Buongiorno [60] :

where nf, f, ρ, and φ denote the nanofluid, base fluid, nanoparticles and particle volume concentration. It should be noted that for calculating the specific heat of nanofluid some researchers have used the following correlation [61] :

The Equation (19) is modified and presented by Buongiorno [60] as follow:

The most commonly used thermal conductivity equation was proposed by Avsec et al. [62] for the mixtures containing micrometer size particles; it is assumed that this equation is applicable for the nanofluids:

In the above equation 
Boundary and Initial Conditions
The geometry used to simulate the temperature distribution was based on a 3D model consisting of cylindrical cell culture dish in which a volume of material with three different layers: a single cell layer (thickness: diameter of a cancer cell of 10 μm and confluency of 99%), a plasmonic gold nanoparticle layer incubated on the cultured lung cancer cell layer (thickness: diameter of one three layer nanoparticle of 85 nm) with cell culture media above these two layers (height: 7 mm). The gold nanoparticles were first internalized by cancer cells and then the volume was irradiated by a 810 nm diode laser with a rectangular output beam at different power densities ranging from 14 to 184 W/cm2 to study the photothermal process.
It should be noted that the Equation (11) is analyzed in the polar coordinates as the experimental domain is cylindrical. It is assumed that the tissue is initially at the physiological temperature of 37˚C:

Another initial condition is
Table 1. Biological and thermophysical parameters used in simulation.

Due to the cylindrical symmetry of the geometry in which the heat equation should be analyzed, temperature elevation was solved in the radial direction only. Three types of boundary conditions are commonly used during the solving of the heat transfer model:


Because of the complexity of the model the following assumptions are considered.
1) Radiation emission from the tissue phantom is neglected because the tissue blackbody intensity is much smaller than the incident laser intensity; 2) tissue optical and thermal properties are thermally stable during the heat transfer process; 3) blood perfusion and thermal evaporation and/or phase change of tissue during the heat transfer process are not considered; 4) fluid phase and nanoparticles are in thermal equilibrium with zero relative velocity.
5. Solution Scheme
The heat transfer behaviour of the system is modeled by using finite element modeling (FEM) using a commercial FEM package (Comsol Multiphysics 3.2a) for solver execution. The software implemented a 2D and 3D cylindrical modeling of the phantom and laser in a cylindrical coordinate system. Figure 5 shows a typical setup of


Figure 5. The meshed structure of computational domain for (a) 2D and (b) 3D simulation. In the 2D simulation, (a) (b) (c) represent the cultured cancer cells, GNPs layer and culture medium, respectively.
the problem by the software. To ensure mesh quality and validity of solution, the mesh was refined until there was less than a 0.5% difference in solution between refinements.
6. Results and Discussion
In this paper, temperature distribution in a GNP-containing cell layer during a continuous wave laser irradiation has been obtained both experimentally and numerically. The experimental trials were conducted in three cases: direct focusing of continuous wave diode laser with different power densities on the i) the cell culture media containing cancer cells only, ii) the cell culture media containing GNSs only, iii) the cell culture media containing both cancer cells and GNSs. The experimental results are compared with the numerical results obtained using solution of thermal wave model of bio-heat transfer equation. The results of numerical modeling obtained from both hyperbolic non-Fourier and parabolic Fourier equation are compared with all three experimental cases. Two common pathways of cell death underlying laser-enabled cell damages to specific cellular structures (e.g. plasmatic membranes, nuclei, cytoskeletons or organelles) are apoptosis and necrosis pathways, depending on the properties of gold nanoparticles (composition, shape and size), their concentration and location in subcellular regions and laser parameters (irradiance, type, and irradiation time) [65] .
6.1. Effect of Continuous Irradiation on Temperature Profile
Figure 6(a) and Figure 6(b) shows the experimental and simulation results obtained from hyperbolic non- Fourier indicating the effect of laser irradiance on the temperature variation of the GNP-containing cancer cell layer at 0.01 mg/ml. As it is observed at lower irradiances the temperature rise is very similar whereas at higher values the experimental results tend to deviate slightly at later time intervals where they becomes more significant i.e., faster deviation at shorter times. The reason for mismatch in their growth pattern can be attributed to isolated boundaries in the model which led to a sharp increase in the temperature of thin cell layer at the bottom of the dish.
Figure 6. (a) Experimentally and (b) numerically-obtained data for temperature rise (ΔT) of QU-DB lung cancer cells incubated with culture medium containing 0.01 mg/ml of MNPS over a period of 3 minutes at various laser irradiance.
6.2. Effect of Concentration of Gold Nanoparticles on Temperature Profile
Based on the SPR absorption in GNPs, an energy relaxation is followed through non-radiative decay channels which results in an increase in kinetic energy, leading to overheating of the local environment around the light- absorbing species. Since, the photothermal effect on tissue is a function of temperature, two different concentrations of GNPs (0.01 mg/ml and 0.1 mg/ml) were used to investigate the local temperature distribution and thermolysis in in-vitro culture medium. By using an appropriate value of GNPs concentration, c for the plasmonic heating term in Equation (17), we analyzed the influence of nanoparticles on the thermal history at 184 W/cm2. It is clear from Figure 7 that the maximum temperature at 140 s using 0.1 mg/ml is higher than 0.01 mg/ml.
The increase in temperature by increasing the concentration of GNSs can be due to their higher density arrangement on the cell membrane and the possibility of Au NSs aggregation, hence resulting in a stronger LSPR and thus more efficient photothermal effects. Figure 8(a) and Figure 8(b) illustrates the temperature contours of irradiated culture medium with and without MNSs. As it is normally expected, the distribution of laser irradiance follows a Gaussian mode, however, the straight path of temperature gradient in our case is due to the rectangular laser beam used for irradiation.
6.3. Effect of Fourier and Non-Fourier Model on Temperature Profile
The experimental and the numerical results are compared using thermal wave model of bio-heat transfer equation. It is observed that experimentally measured temperature distribution is in good agreement with that predicted by simulation of non-Fourier hyperbolic heat conduction model. Temperature contours of irradiated cancer cells incubated with 0.01 mg/ml of MNSs based on Fourier and non-Fourier conduction model are shown in Figure 9.
6.4. Comparison of Results of 2D and 3D Modeling
The geometry used to simulate TWMBT equation was based on a 2D and 3D model consisting of a cylindrical cell culture dish including a cancer cell layer situated at the bottom of the dish surrounded by GNPs and culture media. Temperature changes of irradiated cancer cells at 184 W/cm2using 0.01 mg/ml of MNSs for experimental, 2D and 3D simulation are shown in Figure 10. The boundary and slice representation of 3D temperature gradients are presented in Figure 11 where the spatio-temporal temperature distribution of irradiated MNSs-laden cancer cells is clearly distinguished with its maximum at the center shown by red.
7. Conclusion
Within the framework of thermal wave model of bio-heat transfer (TWMBT) equation, the spatio-temporal temperature distribution of GNSs surrounded by QU-DB lung cancer cells was studied. The effect of different parameters such as irradiance, GNSs concentration, Fourier or non-Fourier model and dimensionality was numerically investigated using a commercial FEM package. Due to larger size of nanoshells, their absorption
Figure 7. Experimentally and numerically-obtained data for temperature rise (ΔT) of QU-DB lung cancer cells incubated with culture medium containing various concentrations of MNPs (0.01 and 0.1 mg/ml) over a period of 3 minutes at 184 W/cm2.
Figure 8. Temperature contour of (a) irradiated cancer cells incubated with MNPs-free medium (MNPs concentration = 0), (b) irradiated cancer cells incubated with MNPs-containing medium (MNPs concentration = 0.01 mg/ml) and (c) irradiated MNPs suspended in culture medium (MNPs concentration = 0.01 mg/ml) without cancer cells. Laser power density in all cases is 184 W/cm2.
Figure 9. Temperature contours of irradiated cancer cells incubated with MNPs-containing medium (MNPs concentration = 0.01 mg/ml) at power density of 184 W/cm2. (a) Numerically-obtained heat gradient based on Fourier and (b) non-Fourier conduction model.
Figure 10. Dimensionality effects on the profile of irradiated QU-DB lung cancer cells incubated with MNPs-containing culture medium (MNPs concentration = 0.01 mg/ml) over a period of 150 seconds at the power density of 184 W/cm2. Simulation trials conducted based on both (a) non-Fourier and (b) Fourier conduction model.
Figure 11. (a) Boundary and (b) slice representation of 3D temperature contours of irradiated cancer cells incubated with MNPs-containing medium (MNPs concentration = 0.01 mg/ml) at power density of 184 W/cm2. Black edges in (b) indicates the computational domain.
cross-section is quite large as a result of which a higher temperature increase can be expected. In vitro study of thermal destruction of cancer cells in laser-heated GNSs showed that the cell killing rate is proportional to the laser power density, irradiation time and GNSs concentration. A maximum temperature rise of 6˚C was achieved at 184 W/cm2 and concentration of 0.01 mg/ml. The results of temperature change obtained from experiment and simulation were in good agreement. The simulation data for the temperature history over 160 seconds showed that non-Fourier heat conduction model gives a more accurate temperature profile than Fourier equation when compared with the experimental data. More deviation of Fourier parabolic heat conduction model from the experimental measurements is mainly attributed to the elimination of thermal relaxation time τ which leads to a rapid and higher temperature rise. The experimentally measured temperature distribution showed a better agreement with 3D modeling of both hyperbolic and parabolic heat conduction model than 2D model. In practical biomedical applications, it implies that an efficient nano-photo hyperthermia can be achieved due to more uniform spatial temperature distribution of plasmonic GNSs as shown by the temperature contours.
References
- World Health Organization. http://www.who.int/
- Mansoori, A.G., Mohazzabi, P., McCormack, P. and Jabbari, S. (2007) World Review of Science, Technology and Sustainable Development, 4, 226-257. http://dx.doi.org/10.1504/WRSTSD.2007.013584
- Choi, Y.E., Kwak, J.W. and Park, J.W. (2010) Sensors, 10, 428-455. http://dx.doi.org/10.3390/s100100428
- Srinivas, P.R., Barker, P. and Srivastava, S. (2002) Laboratory Investigation, 82, 657-662. http://dx.doi.org/10.1038/labinvest.3780460
- Jolesz, F.A. and Hynynen, K. (2002) Cancer Journal, 1, S100-S112.
- Seki, T., Wakabayashi, M., Nakagawa, T., Imamura, M., Tamai, T., Nishimura, A., Yamashiki, N., Okamura, A. and Inoue, K. (1999) Cancer, 85, 1694-1702. http://dx.doi.org/10.1002/(SICI)1097-0142(19990415)85:8<1694::AID-CNCR8>3.0.CO;2-3
- Gazelle, G.S., Goldberg, S.N., Solbiati, L. and Livraghi, T. (2000) Radiology, 217, 633-646. http://dx.doi.org/10.1148/radiology.217.3.r00dc26633
- Mirza, A.N., Fornage, B.D., Sneige, N., Kuerer, H.M., Newman, L.A., Ames, F.C. and Singletary, S.E. (2001) Cancer Journal, 7, 95-102.
- Khosroshahi, M.E. and Ghazanfari, L. (2012) Iranian Journal of Medical Physics, 9, 253-263.
- Amin, Z., Donald, J.J., Masters, A., Kant, R. Steger, A.C., Bown, S.G. and Lees, W.R. (1993) Radiology, 187, 339- 347. http://dx.doi.org/10.1148/radiology.187.2.8475270
- Nolsøe, C.P., Torp-Pedersen, S., Burcharth, F., Horn, T., Pedersen, S., Christensen, N.E., Olldag, E.S., Andersen, P.H., Karstrup, S., Lorentzen, T., et al. (1993) Radiology, 187, 333-337. http://dx.doi.org/10.1148/radiology.187.2.8475269
- Vogl, T.J., Mack, M.G., Müller, P.K., Straub, R., Engelmann, K. and Eichler, K. (1999) European Radiology, 9, 1479- 1487. http://dx.doi.org/10.1007/s003300050874
- Maiman, T.H. (1960) Nature, 187, 493-494. http://dx.doi.org/10.1038/187493a0
- Kapany, N.S., Peppers, N.A., Zweng, H.C. and Flocks, M. (1963) Nature, 199, 146-149. http://dx.doi.org/10.1038/199146a0
- Hall, R.R., Beach, A.D., Baker, E. and Morison, P.C.A. (1971) Nature, 232, 131-132. http://dx.doi.org/10.1038/232131a0
- McKenzie, A.L. and Carruth, J.A. (1984) Physics in Medicine and Biology, 29, 619-641. http://dx.doi.org/10.1088/0031-9155/29/6/001
- Wang, K.K.H., Finlay, J.C., Busch, T.M., Hahn, S.M. and Zhu, T.C. (2010) Journal of Biophotonics, 3, 304-318. http://dx.doi.org/10.1002/jbio.200900101
- Khosroshahi, M.E. and Ghazanfari, L. (2012) Materials Chemistry and Physics, 133, 55-62. http://dx.doi.org/10.1016/j.matchemphys.2011.12.047
- Simon, T., Boca-Farcau, S., Gabudean, A.M., Baldeck, P. and Astilean, S. (2013) Journal of Biophotonics, 6, 950-959.
- Nicolodelli, G., Angarita, D.P.R., Inada, N.M., Tirapelli, L.F. and Bagnato, V.S. (2014) Journal of Biophotonics, 7, 631-637.
- Huang, X., Jain, P.K., El-Sayed, I.H. and El-Sayed, M.A. (2007) Nanomedicine, 2, 681-693. http://dx.doi.org/10.2217/17435889.2.5.681
- Skrabalak, S.E., Chen, J., Au, L., Lu, X., Li, X. and Xia, Y. (2007) Advanced Materials, 19, 3177-3184. http://dx.doi.org/10.1002/adma.200701972
- Loo, C., Lowery, A., Halas, N.J., West, J.L. and Drezek, R. (2005) Nano Letters, 5, 709-711. http://dx.doi.org/10.1021/nl050127s
- Khosroshahi, M.E., Nourbakhsh, M.S. and Ghazanfari, L. (2011) Journal of Modern Physics, 2, 944-953. http://dx.doi.org/10.4236/jmp.2011.29112
- Khanadeev, V.A., Khlebtsov, B.N., Staroverov, S.A., Vidyasheva, I.V., Skaptsov, A.A., Ileneva, E.S., Bogatyrev, V.A., Dykman, L.A. and Khlebtsov, N.G. (2011) Journal of Biophotonics, 4, 74-83.
- Avetisyan, Y.A., Yakunin, A.N. and Tuchin, V.V. (2012) Journal of Biophotonics, 5, 734-744. http://dx.doi.org/10.1002/jbio.201100074
- Hasannejad, Z. and Khosroshahi, M.E. (2013) Optics Materials, 35, 644-651. http://dx.doi.org/10.1016/j.optmat.2012.10.019
- Loo, C., Hirsch, L., Lee, M.H., Chang, E., West, J., Halas, N.J. and Drezek, R. (2005) Optics Letters, 30, 1012-1014. http://dx.doi.org/10.1364/OL.30.001012
- Sokolov, K., Follen, M., Aaron, J., Pavlova, I., Malpica, A., Lotan, R. and Richards-Kortum, R. (2003) Cancer Research, 63, 1999-2004.
- Kumar, S., Aaron, J. and Sokolov, K. (2008) Nature Protocols, 3, 314-320. http://dx.doi.org/10.1038/nprot.2008.1
- Jain, R.K. (1999) Annual Review of Biomedical Engineering, 1, 241-263. http://dx.doi.org/10.1146/annurev.bioeng.1.1.241
- Khosroshahi, M.E. and Ghazanfari, L. (2012) Materials Science and Engineering C, 32, 1043-1049.
- Pankhurst, Q.A., Connolly, J., Jones, S.K. and Dobson, J.J. (2003) Journal of Physics D: Applied Physics, 36, R167- R181. http://dx.doi.org/10.1088/0022-3727/36/13/201
- Lewinski, N., Colvin, V. and Drezek, R. (2008) Small, 4, 26-49. http://dx.doi.org/10.1002/smll.200700595
- Murphy, C.J., Gole, A.M., Stone, J.W., Sisco, P.N., Alkilany, A.M., Goldsmith, E.C. and Baxter, S.C. (2008) Accounts of Chemical Research, 41, 1721-1730. http://dx.doi.org/10.1021/ar800035u
- Elliott, A., Schwartz, J., Wang, J., Shetty, A., Hazle, J. and Stafford, J.R. (2008) Lasers in Surgery and Medicine, 40, 660-665. http://dx.doi.org/10.1002/lsm.20682
- Vera, J. and Bayazitoglu, Y. (2009) International Journal of Heat and Mass Transfer, 52, 3402-3406. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2009.02.014
- Pennes, H.H. (1948) Journal of Applied Physiology, 1, 93-122.
- Khosroshahi, M.E. and Ghazanfari, L. (2012) Materials Chemistry and Physics, 133, 55-62. http://dx.doi.org/10.1016/j.matchemphys.2011.12.047
- Pham, T., Jackson, J.B., Halas, N. and Lee, T.R. (2002) Langmuir, 18, 4915-4920. http://dx.doi.org/10.1021/la015561y
- Ji, X., Ruping, S., Elliott, A.M., Stafford, R.J., Esparza-Coss, E., Bankson, J.A., et al. (2007) Journal of Physical Chemistry C, 111, 6245-6251. http://dx.doi.org/10.1021/jp0702245
- Joanitti, G.A., Azevedo, R.B. and Freitas, S.M. (2010) Cancer Letters, 293, 73-81. http://dx.doi.org/10.1016/j.canlet.2009.12.017
- Kong, G., Braun, R.D. and Dewhirst, M.W. (2000) Cancer Research, 60, 4440-4445.
- Lee, Y.Y., Wong, K.T., Tan, J., Toh, P.C., Mao, Y., Brusic, V., et al. (2009) Journal of Biotechnology, 143, 34-43. http://dx.doi.org/10.1016/j.jbiotec.2009.05.013
- Nikfarjam, M., Muralidharan, V. and Christophi, C. (2005) Journal of Surgical Research, 127, 208-223. http://dx.doi.org/10.1016/j.jss.2005.02.009
- Clark, A.W., Robins, H.I., Vorpahl, J.W. and Yatvin, M.B. (1983) Cancer Research, 43, 1716-1723.
- Soto-Cerrato, V., Montaner, B., Martinell, M., Vilaseca, M., Giralt, E. and Perez-Tomas, R. (2005) Biochemical Pharmacology, 71, 32-41. http://dx.doi.org/10.1016/j.bcp.2005.10.020
- Joanitti, G.A., Azevedo, R.B. adn Freitas, S.M. (2010) Cancer Letters, 293, 73-81. http://dx.doi.org/10.1016/j.canlet.2009.12.017
- Pustovalov, V., Astafyeva, L. and Jean, B. (2009) Nanotechnology, 20, Article ID: 225105.
- Missirlis, Y.F. and Spiliotis, A.D. (2002) Biomolecular Engineering, 19, 287-294. http://dx.doi.org/10.1016/S1389-0344(02)00033-3
- Joseph, D.D. and Preziosi, L. (1989) Reviews of Modern Physics, 61, 41-73. http://dx.doi.org/10.1103/RevModPhys.61.41
- Cahill, D.G., Ford, W.K., Goodson, K.E., Mahan, G.D., Majumdar, A., Maris, H.J., Merlin, R. and Phillpot, S.R. (2003) Journal of Applied Physics, 93, 793-818. http://dx.doi.org/10.1063/1.1524305
- Cattaneo, C. (1958) Comptes Rendus, 247, 431-433.
- Vernotte, P. (1961) Comptes Rendus, 252, 2190-2191.
- Tzou, D.Y. (1996) Macro- to Microscale Heat Transfer, the Lagging Behavior. Taylor & Francis, Washington DC.
- Liu, J., Zhang, X., Wang, C., Lu, W. and Ren, Z. (1997) Chinese Science Bulletin, 42, 289-292. http://dx.doi.org/10.1007/BF02882462
- Welch, A.J. and van Gemert, M.J.C. (1995) Optical-Thermal Response of Laser-Irradiated Tissue. Plenum Press, New York. http://dx.doi.org/10.1007/978-1-4757-6092-7
- Duderstadt, J. and Hamilton, L. (1976) Nuclear Reactor Analysis. Wiley, New York.
- Wyman, D., Patterson, M. and Wilson, B. (1989) Applied Optics, 28, 5243-5249. http://dx.doi.org/10.1364/AO.28.005243
- Buongiorno, J. (2006) Journal of Heat Transfer, 128, 240-250. http://dx.doi.org/10.1115/1.2150834
- Pak, B.C. and Cho, Y.I. (1998) Experimental Heat Transfer, 11, 151-170. http://dx.doi.org/10.1080/08916159808946559
- Avsec, J. and Oblak, M. (2007) International Journal of Heat and Mass Transfer, 50, 4331-4341. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2007.01.064
- Carrara, N. (2010) Dielectric Properties of Body Tissues. http://niremf.ifac.cnr.it/tissprop/
- Duck, F.A. (1990) Physical Properties of Tissue: A Comprehensive Reference Book. Academic Press, London.
- Tong, L., Zhao, Y., Huff, T.B., Hansen, M.N., Wei, A. and Cheng, J.X. (2007) Advanced Materials, 19, 3136-3141. http://dx.doi.org/10.1002/adma.200701974












