Journal of Modern Physics
Vol.05 No.16(2014), Article ID:51069,4 pages
10.4236/jmp.2014.516170
Direct Experimental Evidence of the Statistical Nature of the Electron Gas in Superconducting Films
Mario Iannuzzi, Massimiliano Lucci, Ivano Ottaviani
Physics Department, University of Rome “Tor Vergata”, Rome, Italy
Email: iannuzzi@roma2.infn.it
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 August 2014; revised 21 September 2014; accepted 18 October 2014
ABSTRACT
In an Nb film an alternate electrical current is partitioned at a Y-shaped obstacle into two splitted beams. The intensity-fluctuation correlation of the two beams (cross-correlation) and the intensity-fluctuation correlation of one beam (auto-correlation) are measured within a low-frequency bandwidth as a function of the incident beam intensity, at temperatures T above or below the temperature Tc of the superconductive transition. The results of these measurements reveal the statistical nature of the electron gas in the normal film and in the superconducting film. The conceptual scheme of the present experiment is a version of the Hanbury Brown and Twiss (HBT) experiment, here adopted for a gas of particles in a solid.
Keywords:
Superconductivity, Bose-Condensation

1. Introduction
The Cooper pairs, which play the fundamental role in the BCS theory of low-temperature superconductivity, are generally described, although with explicit caution, as bound pairs of electrons in a highly coherent state; the formation of few pairs encourages the formation of others in a cooperative way, a tendency quite analogous to what happens in a Bose condensation. For instance, with Feynman’s wording [1] : “The two electrons which form the pair are not like a point particle… They are really spread over a considerable distance… The mean distance between pairs is relatively smaller than the size of a single pair. Several pairs are occupying the same space at the same time… We will accept, however, the idea that electrons do, in some manner or other, work in pairs… behaving more or less like particles. Since electron pairs are bosons, when there are a lot of them in a given state there is an especially large amplitude for other pairs to go to the same state. So nearly all of the pairs will be locked down at the lowest energy in exactly the same state…”.
Now, such a general and qualitative description of the physical nature of the Cooper pairs being universally taken as true, it would be nice to verify it by a direct experimental test. Such a test is feasible, as we discuss in the present letter describing the experiment we have performed.
First we have argued that the physical nature (bosonic, fermionic, or classical) of a beam of particles can effectively be distinguished by measuring its temporal intensity-correlation function. In this regard we may recall that Hanbury Brown and Twiss (HBT) [2] long ago measured the bunching effect of a beam of optical photons, so showing their bosonic nature; and more recently the antibunching effect of fermions was observed in a beam of free non-interacting neutrons [3] . Other fermionic and bosonic systems have also been studied [4] [5] . These results have convinced us that a HBT experiment might bring directly to light the statistical properties of a beam of Cooper pairs, and have motivated the measurements presented below in this Letter.
2. Method
Let  be the time-dependent current intensity of a beam of charged particles, and ΔI it’s fluctuation around the average intensity
be the time-dependent current intensity of a beam of charged particles, and ΔI it’s fluctuation around the average intensity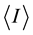 , due to the fluctuation ΔN of the number of particles N detected within a certain time interval. A classical stream of carriers originating from an equilibrium reservoir will obey Poisson statistics with
, due to the fluctuation ΔN of the number of particles N detected within a certain time interval. A classical stream of carriers originating from an equilibrium reservoir will obey Poisson statistics with
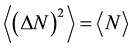 , whereas a stream of Bose carriers will obey Bose-Einstein statistics with
, whereas a stream of Bose carriers will obey Bose-Einstein statistics with 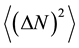 larger than
larger than
 , and a stream of Fermi carriers will obey Fermi-Dirac statistics with
, and a stream of Fermi carriers will obey Fermi-Dirac statistics with  smaller than
smaller than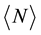 . Now, along the lines of the HBT pioneering experiment on optical photons, let an experiment on quantum carriers, instead of measuring the intensity fluctuations of a single beam, measure the intensity fluctuation correlations
. Now, along the lines of the HBT pioneering experiment on optical photons, let an experiment on quantum carriers, instead of measuring the intensity fluctuations of a single beam, measure the intensity fluctuation correlations 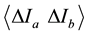 between two partial beams, Ia and Ib, originating from a beam splitter. General expressions giving the theoretical cross correlation
between two partial beams, Ia and Ib, originating from a beam splitter. General expressions giving the theoretical cross correlation  can be obtained from the cross correlation function
can be obtained from the cross correlation function 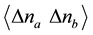 of the occupation numbers, na and nb, of the two partitioned beams, as it is shown in [6] for beams emitted from an equilibrium reservoir ( of bosons or fermions ).
of the occupation numbers, na and nb, of the two partitioned beams, as it is shown in [6] for beams emitted from an equilibrium reservoir ( of bosons or fermions ).
In the presence of a steady current, provided that , the cross correlation for transport fluctuations of the two beams Ia and Ib, in small conductors and in the limit of low frequencies, has been derived theoretically as [6] :
, the cross correlation for transport fluctuations of the two beams Ia and Ib, in small conductors and in the limit of low frequencies, has been derived theoretically as [6] :
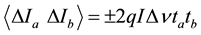 (1)
(1)
where 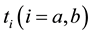 is the transmission probability of the portioned beam-i, I is the total current intensity (for an alternate current we adopt the notation
is the transmission probability of the portioned beam-i, I is the total current intensity (for an alternate current we adopt the notation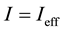 ), q is the carrier charge (q = e for fermions and q = 2e for Coo- per pairs), and ∆n is a flat frequency band-width within the low-frequency spectrum of the current fluctuations. Here a small electrical conductor is a conductor of small resistance, such that the wavelike transport of carriers preserves phase coherence over distances larger than the distance between the two contacts of the beam partition. With a = b (auto-correlation), the sign of the correlation is always positive, both for fermions and bosons, and
), q is the carrier charge (q = e for fermions and q = 2e for Coo- per pairs), and ∆n is a flat frequency band-width within the low-frequency spectrum of the current fluctuations. Here a small electrical conductor is a conductor of small resistance, such that the wavelike transport of carriers preserves phase coherence over distances larger than the distance between the two contacts of the beam partition. With a = b (auto-correlation), the sign of the correlation is always positive, both for fermions and bosons, and
formula (1) reduces to the standard expression for shot noise . With
. With 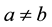 (cross-correlation),
(cross-correlation),
for fermions the correlation is always negative. For bosons, even though as a rule the correlation would be negative because flux conservation requires that an increase at one partition must be compensated by a decrease at the other partition, yet there are many circumstances under which the sign of the cross-correlations is positive, among them, the conductors with one of the two terminals partitioned into two leads, like our Nb samples [6] . Experimental evidence of the anticorrelation predicted by formula (1) for a gas of fermions was obtained on a beam of electrons in the quantum Hall regime [7] .
3. Experiment and Results
Let us consider now superconducting films. Obviously, expression (1) with negative sign applies also to such films at temperatures above the critical temperature Tc (Fermi gas); differently, at temperatures below Tc the Cooper pairs should behave like bosons with consequent positive cross-correlation at a Y-shaped partition. Yet, the fluctuation correlations cannot be discussed without addressing the cooperative effect of such pairs analo- gous to the Bose condensation transition: therefore, now the incident state (i.e. the state arriving at the partition obstacle ) is a single state of energy and momentum containing a precise number of many particles (nearly all of the pairs), and the fluctuations ΔIa and ΔIb, which are a consequence of the probabilistic transmission either in partition a or b, will have opposite signs if measured at the same time. With nI as the occupation number of the incident state containing a precise number of particles, and na, nb as the occupation numbers of the transmitted states, the cross-correlation is

This yields:


Consequently, the expectation value of the correlation is still given by expression (1), with q = e.
An experiment aimed at enlightening the statistical nature of the Cooper pairs will therefore measure the cross correlation 
We have performed an experiment whose general scheme is represented in Figure 1. The correlator outcome is a voltage VC proportional to
Figure 1. Scheme of the experiment on Nb films. The frequency of the incident beam I was 3 MHz. The total length of all Y-shaped specimens was 7 mm, their cross section ≤ 400 × 0.3 um2, and their electrical resistance at room temperature ≤ 25 Ohm. The pass band of the filters F was in the range 300 Hz to 600 KHz. Correlator readings VC are proportional to
Figure 2. Transport fluctuation correlation at 6.5 K (squares) and 15.0 K (circles) as a function of the incident beam intensity (I = Ieff) in a Y-shaped Nb film of small resistance (R = 200 Ohm, at 293 K) and superconductive transition at Tc = 9.2 K. Current independent fluctuations, such as thermal noise and residual electronic noise, have been subtracted from the readings of VC. The vertical size of the squares represents the experimental error on VC. The slope of both curves yields
Figure 3. As in Figure 2, at T = 293 K. The slope of the curves yields
source was a current source, and the two exit terminals of the Y-partition, virtually grounded, were connected to a current-voltage converter which allowed to measure separately Ia and Ib. The width of the pass-band filters was ∆n = 300 Hz - 600 KHz for the all measurements.
All the specimens showed up the same behaviour; and Figure 2 shows the results recorded with the 20W- specimen at T = 15.0 K (>Tc = 9.2 K) and T = 6.5 K (

4. Conclusion
We have performed an experiment whose results give direct evidence of the statistical nature of the electron gas in Nb films, at temperatures above Tc (fermions ) and at temperatures below Tc (Cooper pairs in a single state of energy and momentum). The conceptual scheme of the experiment, which measures the intensity-fluctuation correlation of two beams of particles partitioned off at a Y-shaped obstacle, is the HBT (Hanbury Brown and Twiss) scheme, here adapted to the electron gas in a conductor. For lack of availability of proper samples, we could not perform an analogous experiment with high-temperature superconductors.
Cite this paper
MarioIannuzzi,MassimilianoLucci,IvanoOttaviani, (2014) Direct Experimental Evidence of the Statistical Nature of the Electron Gas in Superconducting Films. Journal of Modern Physics,05,1708-1712. doi: 10.4236/jmp.2014.516170
References
- 1. Feynman, R.P. (1970) Lectures on Physics. Addison-Wesley Pu.Co., Reading.
- 2. Hanbury Brown, R. and Twiss, R.Q. (1956) Nature, 177, 27-29.
http://dx.doi.org/10.1038/177027a0 - 3. Iannuzzi, M., Messi, R., Moricciani, D., Orecchini, A., Sacchetti, F., Facchi, P. and Pascazio, S. (2011) Physical Review A, 84, 015601
http://dx.doi.org/10.1103/PhysRevA.84.015601 - 4. Schellekens, M., Hoppeler, R., Perrin, A., Viana Gomes, J., Boiron, D., Aspect, A. and Westbrook, C.I. (2005) Science, 310, 648-651.
http://dx.doi.org/10.1126/science.1118024 - 5. Jeltes, T., McNamara, J.M., Hogervorst, W., Vassen, W., Krachmalnicoff, V., Schellekens, M., Perrin, A., Chang, H., Boiron, D., Aspect, A. and Westbrook, C.I. (2007) Nature, 445, 402; and references therein.
http://dx.doi.org/10.1038/nature05513 - 6. Buttiker, M. (1992) Physical Review B, 46, 12485.
http://dx.doi.org/10.1103/PhysRevB.46.12485 - 7. Henny, M., Oberholzer, S., Strunk, C., Heinzel, T., Ensslin, K., Holland, M. and Schonenberger, C. (1999) Science, 284, 296.
http://dx.doi.org/10.1126/science.284.5412.296
NOTES
1We may note that the temptation to find an approach to our experiment, alternative to the one presented here, in terms of the Ising model would not appear fruitful. We have measured correlations between one-dimensional electric currents near the quantum superconducting transition of the electric gas in Nb films. Vice versa, the Ising model is a lattice- based classical model whose one-dimensional version has no phase transition. The application of the two-dimensional version (Onsager solution) would appear inappropriate to represent our experimental scheme, and in any case it would require the difficult task to include quantum effects, “lattice-gas” sites, momentum of charged particles.





