Journal of Modern Physics
Vol.4 No.8(2013), Article ID:36326,10 pages DOI:10.4236/jmp.2013.48153
Dynamics of Particle in Confined-Harmonic Potential in External Static Electric Field and Strong Laser Field
1Department of Physics, Maitreyi College, University of Delhi, New Delhi, India
2Department of Physics and Electronics, Rajdhani College, University of Delhi, New Delhi, India
3Department of Physics, Swami Shraddhanand College, University of Delhi, New Delhi, India
Email: *vijit_vin@yahoo.co.in
Copyright © 2013 Shalini Lumb et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 23, 2013; revised May 28, 2013; accepted June 19, 2013
Keywords: Confined-Harmonic Oscillator; B-Polynomial; Transition Probability
ABSTRACT
Dynamics of a particle in confined-harmonic potential, subjected to external static electric and time-dependent laser fields is studied. The energy levels and wave functions of unperturbed harmonic oscillator are evaluated using B-polynomial Galerkin method. Matrix formulation is used throughout the procedure. This procedure is very simple and efficient in comparison with other methods. Modifications of wave functions and energy levels due to static electric field are also calculated. Finally, absorption spectra of such a driven oscillator are studied and explained.
1. Introduction
The systems for which exact quantum mechanical solutions for Schrödinger equation can be found are few in number, for example, the harmonic oscillator potential and nonrelativistic hydrogen atom. The harmonic oscillator potential is a model of great practical importance, as it approximates any arbitrary potential close to equilibrium. In nanotechnology, potentials of simple shape such as quantum dots are often well approximated by such parabolic potentials. In fact, almost all exactly solvable problems in Quantum Mechanics are harmonic oscillator problems in disguise.
The confined-harmonic oscillator potential plays an important role in many applications of Quantum Mechanics. Such a potential is extensively used to describe the bound states of nonrelativistic systems. It also plays a basic role in chemical and molecular physics. In quantum chemistry, simple harmonic potential is used as a simplified model to describe vibrational motion of two atoms, where, more precise model is the Morse potential. In nonrelativistic quantum mechanics, the Schrödinger equation for this potential has been studied for systems ranging from 1-Dimensional to D-Dimensional Space [1-4]. Such a system has been widely studied as it can be exactly solved and is a very relevant system [5].
The perturbation of quantum harmonic oscillators with external fields has recently attracted a renewed interest due to different aspects of the problem, catalysed by recent developments as follows: 1) quantum dynamics of ion in a Paul trap [6], 2) confining potentials for various quantum heterostructures, which leads to modifications of various physical properties of the media they are composed of [7,8] 3) dynamics of a harmonic oscillator with time-dependent force constant and perturbed by weak quartic anharmonicity [9], 4) need for exact propagators for the anisotropic two-dimensional charged harmonic oscillator in presence of external fields [10].
The effects of external fields on systems under the effect of other types of potentials like pseudo-harmonic oscillator potential have also been explored in literature. For example, the effect on energy levels of a 2D Klein Gordon particle under pseudo-harmonic oscillator interaction has been studied [11]. The Schrödinger equation has been solved for a particle in the general 1D time-dependent linear potential [12]. The quantum motion of an electron driven by a strong time-dependent linear potential in a 1D quantum wire has been investigated and interesting physical properties studied [13]. The possibility of exactly manipulating the quantum motional states of a single particle held in a double cosine potential by using laser beams has been explored [14].
Time-dependent perturbations of such systems have also been studied extensively [15,16]. Explicit wave functions and geometric phases of time-dependent harmonic oscillator in external time-dependent magnetic and electric field have been derived [17]. The exact wave functions and eigenvalues of a 2D time-dependent harmonic oscillator under the influence of a static magnetic field have been calculated [18]. The time evolution of a 2D harmonic oscillator, with time-dependent mass and frequency, in a static magnetic field has also been studied analytically [19].
An electron in confined-harmonic oscillator potential exposed to an external electric field is equivalent to a charged harmonic oscillator in a uniform electric field or a harmonic oscillator in an external dipole field. Such a system has an important role in quantum chemical applications [20]. Recently, O. Kidun and D. Bauer [21] have studied two interacting electrons in harmonic potential driven by a strong laser field. They have studied population dynamics of the system. They have further shown the conditions of complete survival and complete depletion of the ground state of “harmonium”. C. Liang et al. have studied the properties of Hooke’s atom (two electrons interacting with Coulomb potential in an external harmonic oscillator potential) in an arbitrary time-dependent electric field [22]. The dynamics of a perturbed quantum Hooke’s atom exposed to intense ultrashort laser pulses has been studied by Torres and Vicario [23].
The traditional techniques of studying such quantum mechanical systems have lately been supplemented by finite basis set methods like B-spline [3,24-26] and Bernstein-polynomial (B-polynomial) methods [27-29]. Recently, Heidari et al. [30] have investigated the case of Hydrogen atom in spherical cavity using B-spline basis functions. The energy spectra of oneand two-electron atoms centered in an impenetrable spherical box have been calculated by Shi Ting Yun et al. by applying Bspline method [31]. The B-spline basis set is highly flexible and localized which leads to very accurate results. The B-spline basis functions of degree 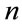 are piecewise polynomials defined on a knot sequence. When the number of B-splines is taken as
are piecewise polynomials defined on a knot sequence. When the number of B-splines is taken as , the basis set becomes a set of continuous B-polynomials over the range under consideration [32]. These B-polynomials are independent of the grid defined by knots and are simple algebraic polynomials. Each of these polynomials is positive and their sum is unity.
, the basis set becomes a set of continuous B-polynomials over the range under consideration [32]. These B-polynomials are independent of the grid defined by knots and are simple algebraic polynomials. Each of these polynomials is positive and their sum is unity.
Polynomials are incredibly useful mathematical tools as they can be calculated very easily and accurately on computer systems. Their evaluation is also fast. They are capable of representing a tremendous variety of functions, can be differentiated and integrated quite easily, and can be pieced together to form spline curves that can approximate any function to any desired accuracy. The B-polynomial method is, therefore, much simpler and efficient. Recently, J. Liu et al. have proposed a new numerical method based on B-polynomials expansion for solving one dimensional elliptic interface problems [33]. B-polynomial basis has also been used for numerically solving differential equations [34-36].
In this paper, the dynamics of an electron in a confined-harmonic potential in static electric and strong laser fields is studied. We have used B-polynomial Galerkin method to solve static field modified harmonic oscillator system. The populations of states modified by static electric field are calculated. The eigenenergies, eigenfunctions and dipole matrix elements of the system are also calculated. The interaction of static field modified confined-harmonic oscillator system with the laser field is taken into account by non-perturbative quasi-energy technique [37-40]. The sequence of the paper is as follows. In Section 2, necessary description of B-polynomials is given. In Section 3, the model under consideration is defined and methods adopted for solving the time-independent as well as time-dependent Schrödinger equation are given. Section 4 deals with interpretation of results and finally, in Section 5, concluding remarks are made.
2. Bernstein-Polynomial Basis
The B-polynomials [41] of degree 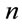 over an interval [a, b] are defined as [27,32]
over an interval [a, b] are defined as [27,32]
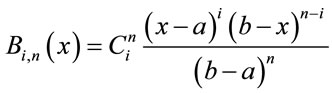 (1)
(1)
for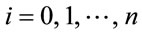 , where
, where
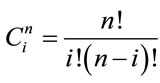 . (2)
. (2)
There are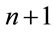 , n-th degree B-polynomials. For mathematical convenience, we usually set
, n-th degree B-polynomials. For mathematical convenience, we usually set 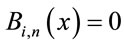 if
if 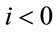 or
or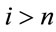 . These
. These 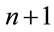 B-polynomials of degree n form a complete basis over the interval
B-polynomials of degree n form a complete basis over the interval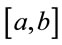 . The B-polynomials can be generated by a recursive relation [33]
. The B-polynomials can be generated by a recursive relation [33]
 . (3)
. (3)
More details of these polynomials are available in literature [24,28,29,32,35,42].
The B-polynomial Galerkin method is employed to solve Schrödinger equation for the present case. In the area of numerical analysis, Galerkin methods are a class of methods for converting a problem such as a differential equation to a linear system of equations. A few of the related formulas used are mentioned here for reference.
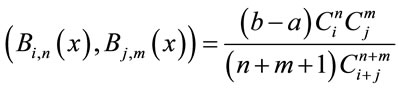 (4)
(4)
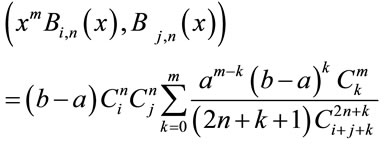 (5)
(5)
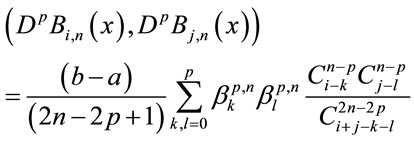 (6)
(6)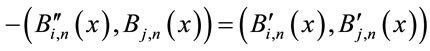 (7)
(7)
where the  are expressed as
are expressed as
 . (8)
. (8)
3. Problem Formulation and Method of Solution
Consider an electron under the effect of a confined-harmonic oscillator potential subjected to an external static electric field , where
, where  is the strength of the electric field. The units used throughout are the atomic units, i.e.,
is the strength of the electric field. The units used throughout are the atomic units, i.e., . The confining potential is given by
. The confining potential is given by
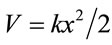 (9)
(9)
where  is a positive constant representing the strength of the potential called the force constant. If the electric dipole moment of the electron is denoted by
is a positive constant representing the strength of the potential called the force constant. If the electric dipole moment of the electron is denoted by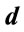 , the potential energy of the electron due to electric field is given by
, the potential energy of the electron due to electric field is given by . The electric dipole moment of the electron is given by
. The electric dipole moment of the electron is given by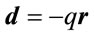 ,
,  representing the position vector of the electron with respect to the origin and
representing the position vector of the electron with respect to the origin and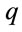 , the charge.
, the charge.
Assume that the electric field is along 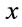 direction, therefore the potential energy term becomes
direction, therefore the potential energy term becomes . The Hamiltonian for the system can be written as
. The Hamiltonian for the system can be written as
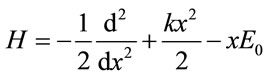 (10)
(10)
Therefore, the Schrödinger equation for the system becomes
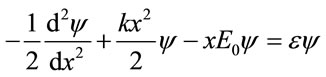 (11)
(11)
A fixed interval 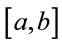 is chosen to study the system. The desired solution may be expanded in terms of a set of continuous polynomials over the closed interval and is given by
is chosen to study the system. The desired solution may be expanded in terms of a set of continuous polynomials over the closed interval and is given by
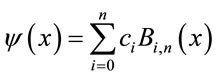 , (12)
, (12)
where 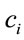 s are the coefficients of expansion and
s are the coefficients of expansion and  are B-polynomials of degree
are B-polynomials of degree 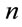 as defined in Section 2. Substituting Equation (12) into Equation (11), taking scalar product with
as defined in Section 2. Substituting Equation (12) into Equation (11), taking scalar product with  on both sides and using Equation (7), Equation (11) becomes
on both sides and using Equation (7), Equation (11) becomes
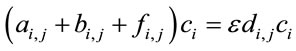 , (13)
, (13)
where the matrix elements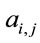 ,
,  ,
, 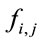 and
and 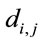 assume closed forms by applying the formulas in Section 2 [29]. Equation (13) in matrix form is
assume closed forms by applying the formulas in Section 2 [29]. Equation (13) in matrix form is
 , (14)
, (14)
where the column matrix 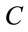 can be determined by solving this symmetric generalized eigenvalue problem.
can be determined by solving this symmetric generalized eigenvalue problem.
The interval 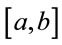 is assumed to be
is assumed to be 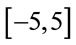 and the number of B-polynomials is taken to be 26. The accuracy and efficiency of the method depend on the number of B-polynomials chosen to construct the approximate solutions. In the present case, the number of B-polynomials is taken to be 26 as there is not much gain in accuracy beyond this value.
and the number of B-polynomials is taken to be 26. The accuracy and efficiency of the method depend on the number of B-polynomials chosen to construct the approximate solutions. In the present case, the number of B-polynomials is taken to be 26 as there is not much gain in accuracy beyond this value. ,
, ,
,  and
and 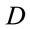 in Equation (14) are 26 × 26 matrices. The standard Fortran EISPACK library is used to solve the generalized eigenvalue problem and find the eigenvalues and eigenvectors. The eigenvalues
in Equation (14) are 26 × 26 matrices. The standard Fortran EISPACK library is used to solve the generalized eigenvalue problem and find the eigenvalues and eigenvectors. The eigenvalues  give the energy levels of the system. The initial eigenvalues for
give the energy levels of the system. The initial eigenvalues for 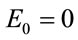 have been found to be correct to five places of decimal. The eigenvectors
have been found to be correct to five places of decimal. The eigenvectors  are used to calculate the corresponding wave functions using Equation (12). These wave functions are the dressed states of the system and are denoted by
are used to calculate the corresponding wave functions using Equation (12). These wave functions are the dressed states of the system and are denoted by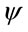 .
.
The system is now exposed to a time-dependent laser field 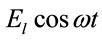 polarized along x-axis, where
polarized along x-axis, where 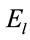 is the strength and
is the strength and  is the frequency of the laser field. The corresponding Hamiltonian becomes
is the frequency of the laser field. The corresponding Hamiltonian becomes
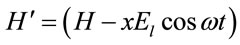 , (15)
, (15)
where 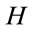 is given by Equation (10). The time-dependent Schrödinger equation for the system is now written as
is given by Equation (10). The time-dependent Schrödinger equation for the system is now written as
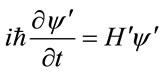 . (16)
. (16)
The solution of Equation (16) in quasi-energy formalism can be written as [43]
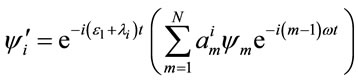 , (17)
, (17)
where  are defined as quasi-energies and
are defined as quasi-energies and 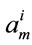 are time-independent eigenvectors to be determined.
are time-independent eigenvectors to be determined.  is the lowest energy level of the system under the effect of static electric field and
is the lowest energy level of the system under the effect of static electric field and 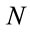 is the number of levels considered. The
is the number of levels considered. The 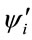 are the dressed states of the system in presence of laser field. The first six energy levels are taken into account and the range of
are the dressed states of the system in presence of laser field. The first six energy levels are taken into account and the range of 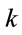 and
and 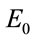 is chosen such that three of them are bound. Substituting the above form of the solution into Equation (16), multiplying by
is chosen such that three of them are bound. Substituting the above form of the solution into Equation (16), multiplying by 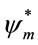 and integrating over
and integrating over 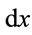 for
for  to
to 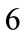 results in a set of six homogeneous coupled equations in
results in a set of six homogeneous coupled equations in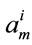 . Using the orthogonality property of wave func tions
. Using the orthogonality property of wave func tions 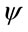 and applying the exact rotating wave approximation [44], these equations assume the following form
and applying the exact rotating wave approximation [44], these equations assume the following form
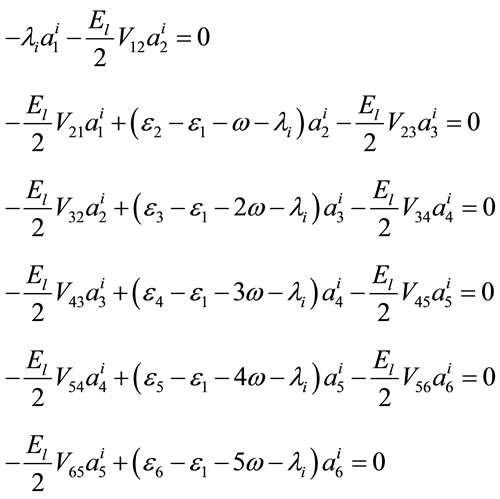 (18)
(18)
The  s are the dipole matrix elements and
s are the dipole matrix elements and 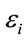 s are the energies of first six levels. The
s are the energies of first six levels. The 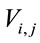 s are defined as
s are defined as
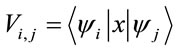 (19)
(19)
and can be easily evaluated using the calculated wave functions . The set of Equations (18) can be solved to determine the quasi-energies
. The set of Equations (18) can be solved to determine the quasi-energies 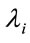 and the corresponding eigenvectors
and the corresponding eigenvectors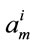 . These eigenvectors can be used to determine the new dressed state wave functions
. These eigenvectors can be used to determine the new dressed state wave functions 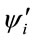 given by Equation (17). In order to solve the set of Equations (18), it is written in matrix form and the corresponding matrix, called the quasi-energy matrix, is diagonalized using standard Fortran subroutines. The calculated eigenvectors are used to determine the transition probabilities to study the absorption spectra. The transition probability from ground state 0 to final state j can be computed from the eigenvectors of the quasi-energy matrix as [45,46]
given by Equation (17). In order to solve the set of Equations (18), it is written in matrix form and the corresponding matrix, called the quasi-energy matrix, is diagonalized using standard Fortran subroutines. The calculated eigenvectors are used to determine the transition probabilities to study the absorption spectra. The transition probability from ground state 0 to final state j can be computed from the eigenvectors of the quasi-energy matrix as [45,46]
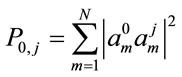 . (20)
. (20)
The photoionization probability,  , i.e., the probability of electron to come out of bound states, is given by
, i.e., the probability of electron to come out of bound states, is given by
 , (21)
, (21)
where  is the sum of the probabilities of the system being in various bound states. Using Equation (21) the phenomenon of photoionization is also studied.
is the sum of the probabilities of the system being in various bound states. Using Equation (21) the phenomenon of photoionization is also studied.
4. Results and Discussion
A single electron in a confined-harmonic oscillator potential is considered to be under the effect of a static electric field. The B-polynomial Galerkin method is used to calculate the dressed states of the confined electron as discussed in Section 3. The variation of eigenvalues for the first six energy states with the static electric field  and force constant
and force constant 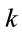 has been studied for this perturbed system. The values have been plotted in Figure 1 relative to those for
has been studied for this perturbed system. The values have been plotted in Figure 1 relative to those for  a.u. so that the changes are evident. It is observed that with the increase in the strength of electric field, the energy values are deviated more from the corresponding values for
a.u. so that the changes are evident. It is observed that with the increase in the strength of electric field, the energy values are deviated more from the corresponding values for  a.u. For a higher force constant, the change in energy values is less.
a.u. For a higher force constant, the change in energy values is less.
According to the standard result from perturbation theory for a charged harmonic oscillator in electric field, the energy levels are always lowered by an amount 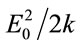 (in atomic units) due to the field. The “dressed” potential [47] in this case is written as
(in atomic units) due to the field. The “dressed” potential [47] in this case is written as
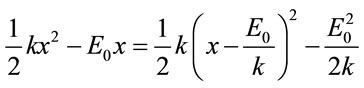 (22)
(22)
which is just a shift of the harmonic potential. From Figure 1 it can be observed that the first two energy levels follow this pattern for low strengths of applied electric field but with the increase in field value the perturbation theory result is not exactly valid and the deviation is found to increase. For the third level it is observed that with increase in k, the relative value is first positive and gradually it becomes negative. The pattern followed by the energy levels is due to the change in wave functions for the system. As a check on the calculations it has been verified that for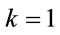 , the energy values for the first few levels, for the range of electric field considered in Figure 1, are in accordance with Equation (22). This is due to the fact that in this case perturbation is small. The increase in energy values with
, the energy values for the first few levels, for the range of electric field considered in Figure 1, are in accordance with Equation (22). This is due to the fact that in this case perturbation is small. The increase in energy values with  is clearly seen in Figure 2 for
is clearly seen in Figure 2 for 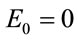 a.u.
a.u.
The effect of  and
and 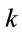 on the dipole matrix elements
on the dipole matrix elements ,
, 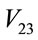 ,
, 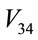 ,
,  and
and 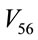 can be seen from Figure 3. The plots with respect to
can be seen from Figure 3. The plots with respect to 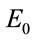 are for different values of
are for different values of  as mentioned in the respective graphs. The values plotted are relative to the corresponding ones for
as mentioned in the respective graphs. The values plotted are relative to the corresponding ones for 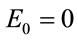 a.u. It may be mentioned that the dipole matrix elements for the harmonic oscillator potential are given as
a.u. It may be mentioned that the dipole matrix elements for the harmonic oscillator potential are given as
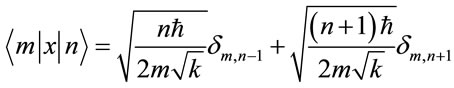 . (23)
. (23)
Since with the introduction of electric field the system is perturbed, this relation would not be valid. With increase in the value of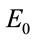 , the dipole elements diverge from the corresponding values for
, the dipole elements diverge from the corresponding values for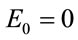 . For example,
. For example,  increases marginally for some
increases marginally for some 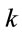 values but
values but 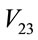

Figure 1. Variation of eigenvalues relative to those for 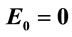 a.u. with respect to static electric field
a.u. with respect to static electric field 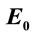 for various values of force constant
for various values of force constant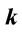 .
.
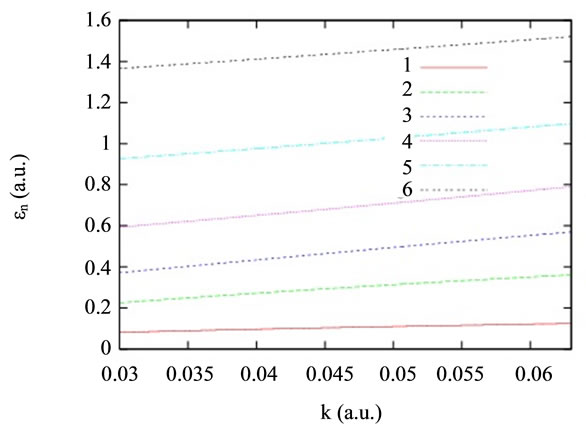
Figure 2. Variation of eigenvalues with respect to force constant  for
for 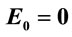 a.u.
a.u.
decreases for all . The effect of electric field is much less for higher
. The effect of electric field is much less for higher  values. The pattern followed by these values is again related to the change in wave functions.
values. The pattern followed by these values is again related to the change in wave functions.
The dipole matrix elements have been plotted with respect to  in Figure 4 for
in Figure 4 for  a.u.
a.u.  and
and  decrease with
decrease with 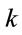 but
but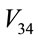 ,
, 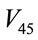 and
and 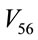 increase with
increase with . The reason for this difference is the fact that in the system only three levels are bound.
. The reason for this difference is the fact that in the system only three levels are bound.
The system is now exposed to laser field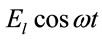 . The response of the perturbed system is now investigated by varying different control parameters like force constant
. The response of the perturbed system is now investigated by varying different control parameters like force constant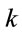 , static electric field
, static electric field , laser field strength
, laser field strength 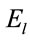 and laser frequency
and laser frequency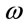 . The variation of transition probabilities for first four energy states with respect to
. The variation of transition probabilities for first four energy states with respect to 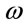 has been depicted in Figure 5 for force constant
has been depicted in Figure 5 for force constant 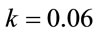 a.u. and laser field
a.u. and laser field 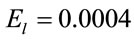 a.u. The plots have been made for different values of static electric field
a.u. The plots have been made for different values of static electric field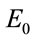 . The values chosen to represent variation of transition probabilities have no special significance. These are just some typical values to show relevant effects. It is observed that the resonant frequency for the first excited state shows red shift with increase in electric field but that for the second excited state shows blue shift. The resonance for the first excited state occurs exactly for
. The values chosen to represent variation of transition probabilities have no special significance. These are just some typical values to show relevant effects. It is observed that the resonant frequency for the first excited state shows red shift with increase in electric field but that for the second excited state shows blue shift. The resonance for the first excited state occurs exactly for 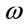 corresponding to the difference in the first two energy levels. The resonance for the second excited state is a two-photon process and occurs at exactly half the energy difference between the ground and the second excited state.
corresponding to the difference in the first two energy levels. The resonance for the second excited state is a two-photon process and occurs at exactly half the energy difference between the ground and the second excited state.

Figure 3. Variation of dipole matrix elements relative to those for 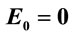 a.u. with respect to
a.u. with respect to 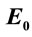 for various values of force constant
for various values of force constant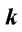 .
.

Figure 4. Variation of dipole matrix elements with respect to force constant 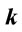 for
for  a.u.
a.u.
The phenomenon of photoionization also shows up for some  values. The peaks for the fourth state, i.e., the first level in the continuum, represent photoionization probability. It is observed that the blue shift for this case is much more than that for the second excited state. It is evident that the first excited state peaks show exact resonance as the probability reaches 0.5. For the peaks corresponding to the second excited state and the fourth level, there is variation in peak strength. This is because the particular frequencies do not represent the condition of exact resonance, i.e., they are slightly off-resonant.
values. The peaks for the fourth state, i.e., the first level in the continuum, represent photoionization probability. It is observed that the blue shift for this case is much more than that for the second excited state. It is evident that the first excited state peaks show exact resonance as the probability reaches 0.5. For the peaks corresponding to the second excited state and the fourth level, there is variation in peak strength. This is because the particular frequencies do not represent the condition of exact resonance, i.e., they are slightly off-resonant.
By keeping  as
as 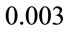 a.u. and
a.u. and 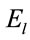 as
as 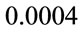 a.u., the variation of transition probabilities with respect to
a.u., the variation of transition probabilities with respect to  has been shown for different values of force constant
has been shown for different values of force constant 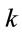 in Figure 6. The figure shows blue shift in resonant frequency for the first as well as the second excited state with increase in value of
in Figure 6. The figure shows blue shift in resonant frequency for the first as well as the second excited state with increase in value of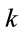 . The blue shift for the second excited state is less as compared to that for the first excited state. The peaks for the fourth state, representing the probability of photoionization, are very prominently seen for
. The blue shift for the second excited state is less as compared to that for the first excited state. The peaks for the fourth state, representing the probability of photoionization, are very prominently seen for 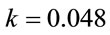 a.u. and
a.u. and 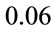 a.u. and also show blue shift. It may be inferred that for these particular frequencies of the laser field, photoionization probability is more than transition probability.
a.u. and also show blue shift. It may be inferred that for these particular frequencies of the laser field, photoionization probability is more than transition probability.
The probability for photoionization can be seen more clearly if total probability of bound states and continuum are represented separately. Figure 7 represents the proba-

Figure 5. Variation of transition probabilities for the first four energy states with respect to the laser frequency 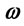 for force constant
for force constant  a.u. and laser field
a.u. and laser field 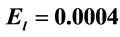 a.u. for different values of static electric field
a.u. for different values of static electric field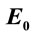 .
.
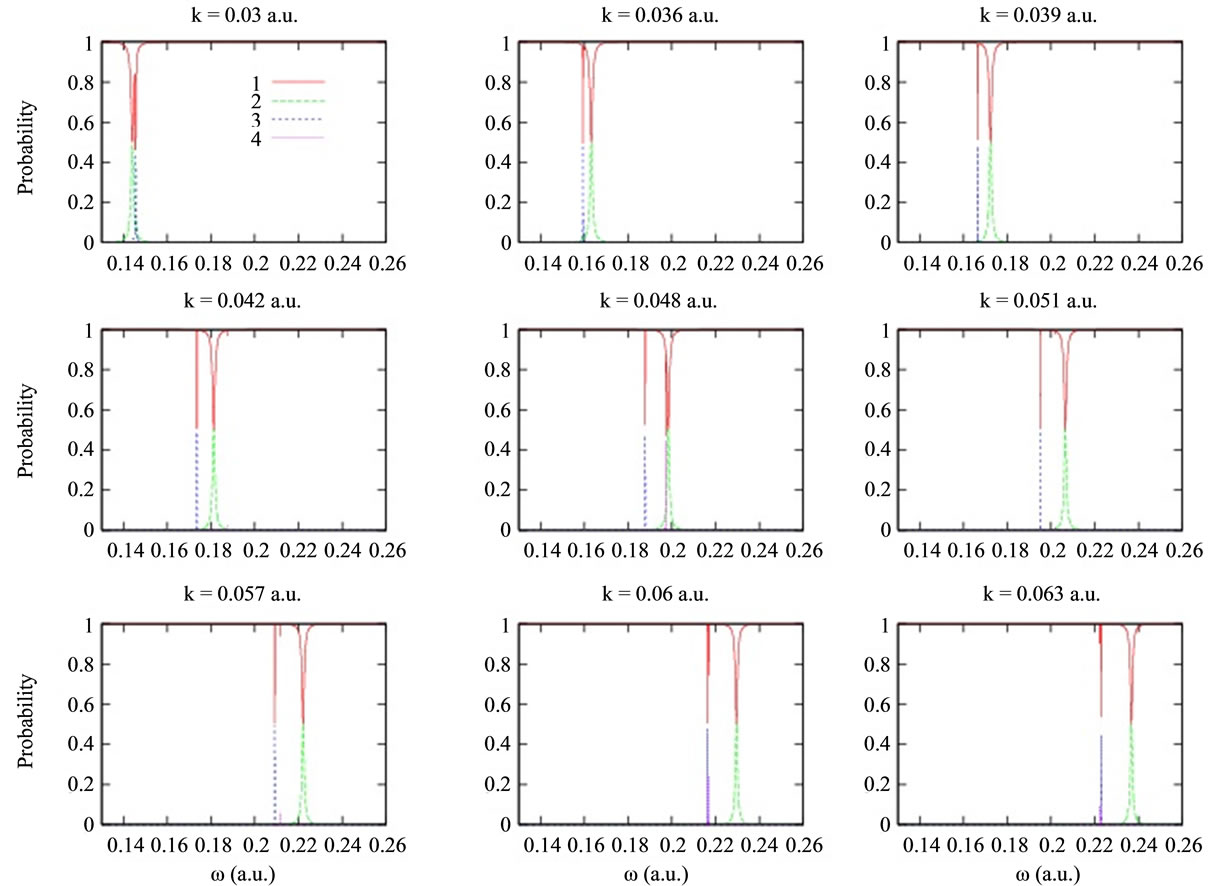
Figure 6. Variation of transition probabilities for the first four energy states with respect to the laser frequency  for static electric field
for static electric field 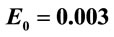 a.u. and laser field
a.u. and laser field  a.u. for different values of force constant
a.u. for different values of force constant .
.
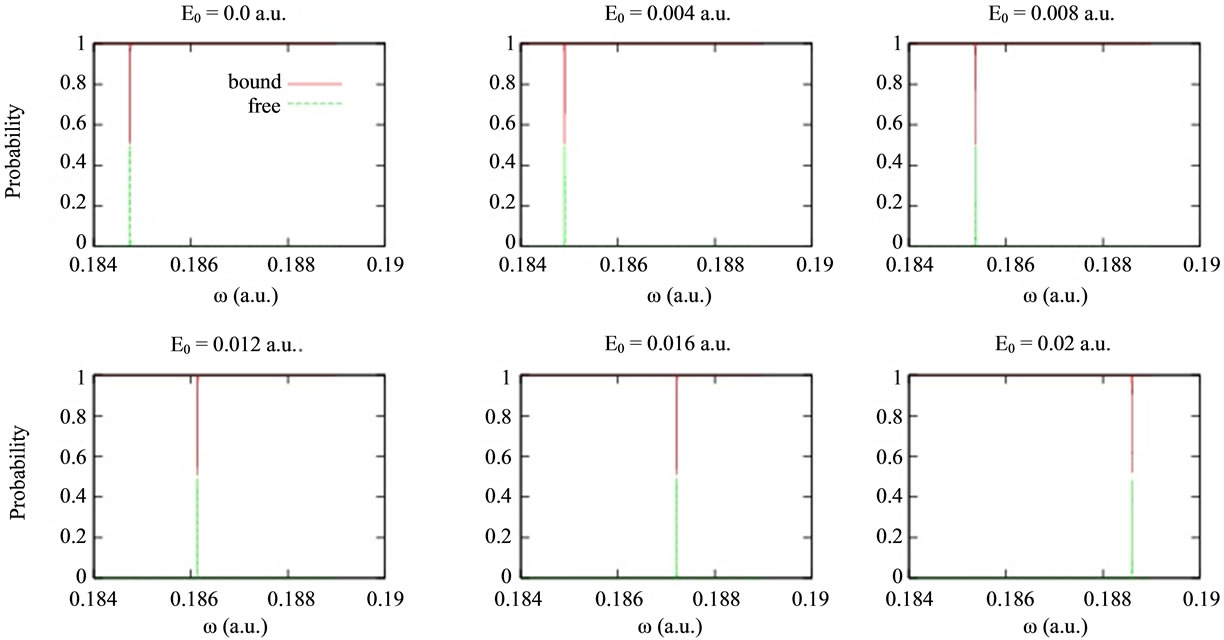
Figure 7. Variation of transition probabilities of the bound and free states with respect to the laser frequency  for force constant
for force constant  a.u. and laser field
a.u. and laser field 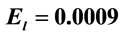 a.u. for different values of static electric field
a.u. for different values of static electric field .
.
Figure 8. Variation of transition probabilities of the bound and free states with respect to the laser frequency 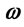 for static electric field
for static electric field 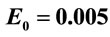 a.u. and laser field
a.u. and laser field 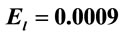 a.u. for different values of force constant k.
a.u. for different values of force constant k.
bility of bound states and free states as a function of laser frequency for 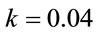 a.u. and
a.u. and 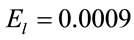 a.u. at different values of
a.u. at different values of . With increase in electric field, blue shift in frequency for photoionization is observed. Similarly, blue shift is observed in Figure 8 where bound and free state probabilities are plotted for a.u. and
. With increase in electric field, blue shift in frequency for photoionization is observed. Similarly, blue shift is observed in Figure 8 where bound and free state probabilities are plotted for a.u. and 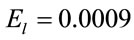 a.u. for different
a.u. for different 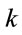 values.
values.
5. Summary and Conclusion
The dynamics of an electron in confined-harmonic oscillator potential under the effect of static electric field and strong laser field is studied. The method based on Bpolynomial basis set is employed to solve the Schrö- dinger equation for the charged confined-harmonic oscillator. The static electric field modifies the wave functions and energies of such confined oscillator and hence the response of the oscillator to external applied laser field gets affected. Photoionization probabilities show strong dependence on the applied static as well as laser field parameters.
REFERENCES
- F. Büyükilic, D. Demirhan and S. F. Ӧzeren, Chemical Physics Letters, Vol. 194, 1992, pp. 9-12. doi:10.1016/0009-2614(92)85734-R
- S. Ikhdair and R. Sever, Journal of Molecular Structure: Theochem, Vol. 806, 2007, pp. 155-158. doi:10.1016/j.theochem.2006.11.019
- S.-H. Dong and Z.-Q. Ma, International Journal of Modern Physics E, Vol. 11, 2002, pp. 155-160. doi:10.1142/S0218301302000752
- L.-Y. Wang, X.-Y. Gu, Z.-Q. Ma and S.-H. Dong, Foundations of Physics Letters, Vol. 15, 2002, pp. 569-576. doi:10.1023/A:1023937704158
- A. Messiah, “Quantum Mechanics,” Elsevier, North-Holland, Amsterdam, 1962.
- S. Moroz, Physical Review A, Vol. 86, 2012, Article ID: 011601. doi:10.1103/PhysRevA.86.011601
- R. Riera, J. L. Marín and R. A. Rosas, “Optical Properties and Impurity States in Nanostructured Materials,” In: H. S. Nalwa, Ed., Handbook of Advanced Electronic and Photonic Materials and Devices, Vol. 6: Nanostructured Materials, Academic Press, San Diego, 2001, Chapter 6.
- L. Lu, W. Xie and H. Hassanabadi, Journal of Applied Physics, Vol. 109, 2011, Article ID: 063108. doi:10.1063/1.3560541
- P. Sarkar, S. Adhikari and S. P. Bhattacharyya, Chemical Physics Letters, Vol. 227, 1994, pp. 187-193. doi:10.1016/0009-2614(94)00795-0
- Z. Zhi-Yuan, Y. Tao and P. Xiao-Yin, Chinese Physics Letters, Vol. 29, 2012, Article ID: 010302. doi:10.1088/0256-307X/29/1/010302
- S. M. Ikhdair and M. Hamzavi, Chinese Physics B, Vol. 21, 2012, Article ID: 110302. doi:10.1088/1674-1056/21/11/110302
- I. Guedes, Physical Review A, Vol. 63, 2001, Article ID: 034102. doi:10.1103/PhysRevA.63.034102
- G. Lu, W. Hai and L. Cai, Physics Letters A, Vol. 357, 2006, pp. 181-187. doi:10.1016/j.physleta.2006.04.047
- K. Hai, W. Hai and Q. Chen, Physics Letters A, Vol. 367, 2007, pp. 445-449. doi:10.1016/j.physleta.2007.03.042
- J. Garnier, Physical Review E, Vol. 60, 1999, pp. 3676- 3687.
- D. C. Khandekar and S. V. Lawande, Journal of Mathematical Physics, Vol. 16, 1975, pp. 384-388. doi:10.1063/1.522511
- Mai-Lin Liang and Y. Jiang, Physics Letters A, Vol. 375, 2010, pp. 1-5. doi:10.1016/j.physleta.2010.10.035
- C. A. S. Ferreira, P. T. S. Alencar, and J. M. F. Bassalo, Physical Review A, Vol. 66, 2002, Article ID: 024103. doi:10.1103/PhysRevA.66.024103
- W. Liu and J. Wang, Journal of Physics A: Mathematical and Theoretical, Vol. 40, 2007, pp. 1057-1063. doi:10.1088/1751-8113/40/5/013
- S. M. Ikhdair, Journal of Modern Physics, Vol. 3, 2012, pp. 170-179. doi:10.4236/jmp.2012.32023
- O. Kidun and D. Bauer, Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 40, 2007, pp. 779- 786. doi:10.1088/0953-4075/40/4/012
- C. Liang, Z. Ping, Y. Tao and P. Xiao-Yin, Communications in Theoretical Physics, Vol. 55, 2011, pp. 565-568. doi:10.1088/0253-6102/55/4/06
- J. F. P. Torres and J. L. S. Vicario, Revista Colombiana de Fίsica, Vol. 41, 2009, pp. 381-384.
- M. I. Bhatti, K. D. Coleman and W. F. Perger, Physical Review A, Vol. 68, 2003, Article ID: 044503. doi:10.1103/PhysRevA.68.044503
- L. B. Zhao and P. C. Stancil, Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 40, 2007, pp. 4347-4354. doi:10.1088/0953-4075/40/22/004
- J. Xi, L. Wu, X. He and B. Li, Physical Review A, Vol. 46, 1992, pp. 5806-5811.
- M. I. Bhatti and W. F. Perger, Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 39, 2006, pp. 553-558. doi:10.1088/0953-4075/39/3/008
- D. D. Bhatta and M. I. Bhatti, Applied Mathematics and Computation, Vol. 174, 2006, pp. 1255-1268. doi:10.1016/j.amc.2005.05.049
- S. Lumb, S. Lumb and V. Prasad, Quantum Matter, Vol. 2, 2013, pp. 314-320.
- A. Heidari, F. K. Jahromi, R. Amiri and M. Ghorbani, Journal of Modern Physics, Vol. 3, 2012, pp. 334-339. doi:10.4236/jmp.2012.34045
- S. Ting-Yun, B. Cheng-Guang and L. Bai-Wen, Communications in Theoretical Physics, Vol. 35, 2001, pp. 195- 200.
- M. I. Bhatti, Advanced Studies in Theoretical Physics, Vol. 3, 2009, pp. 451-460.
- J. Liu, Z. Zheng and Q. Xu, Journal of Applied Mathematics, Vol. 2012, Article ID: 859315. doi:10.1155/2012/859315
- D. Bhatta, Applied Mathematics and Computation, Vol. 206, 2008, pp. 457-464. doi:10.1016/j.amc.2008.09.031
- M. I. Bhatti and P. Bracken, Journal of Computational and Applied Mathematics, Vol. 205, 2007, pp. 272-280. doi:10.1016/j.cam.2006.05.002
- Y. Ordokhani and S. Davaei Far, ISRN Applied Mathematics, Vol. 2011, Article ID” 787694. doi:10.5402/2011/787694
- B. Sharma, V. Prasad and M. Mohan, The Journal of Chemical Physics, Vol. 89, 1988, pp. 1322-1326. doi:10.1063/1.455183
- M. Mohan and V. Prasad, Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 24, 1991, pp. L81- L87.
- U. Arya, B. Dahiya and V. Prasad, Journal of Modern Physics, Vol. 3, 2012, pp. 28-36. doi:10.4236/jmp.2012.31004
- V. Prasad and B. Dahiya, Physica Status Solidi B, Vol. 248, 2011, pp. 1727-1734. doi:10.1002/pssb.201046582
- B. R. Gelbaum, “Modern Real and Complex Analysis,” John Wiley and Swons, New York, 1995.
- M. I. Bhatti and D. D. Bhatta, Physica Scripta, Vol. 73, 2006, pp. 539-544. doi:10.1088/0031-8949/73/6/004
- B. Sharma, V. Prasad, K. L. Baluja and M. Mohan, Zeitschrift für Physik D, Vol. 27, 1993, pp. 65-71.
- S. Chang and V. Minoginb, Physics Reports, Vol. 365, 2002, pp. 65-143.
- J. H. Shirley, Physical Review, Vol. 138, 1965, pp. B979- B987.
- N. Singhal, V. Prasad and M. Mohan, Pramana, Vol. 62, 2004, pp. 883-891.
- E. C. Niculescua and L. M. Burileanu, The European Physical Journal B, Vol. 74, 2010, pp. 117-122. doi:10.1140/epjb/e2010-00060-3
NOTES
*Corresponding author.

