Journal of Modern Physics
Vol.4 No.3(2013), Article ID:28876,5 pages DOI:10.4236/jmp.2013.43054
Ankle Phenomenon in the Cosmic Ray Energy Spectrum
Michigan Center for Theoretical Physics, Randall Laboratory of Physics, University of Michigan, Ann Arbor, USA
Email: tomozawa@umich.edu
Received November 26, 2012; revised January 10, 2013; accepted January 23, 2013
Keywords: Cosmic Rays; Cosmology; Knee Energy; Inflation
ABSTRACT
The author has suggested that the knee phenomenon in the cosmic ray energy spectrum at 3 PeV can be explained as a split between a radiation-dominated expansion and a matter-dominated expansion of an expanding heat bath. The model proposed in 1985, in fact, predicted that high energy cosmic rays are emitted from AGN, massive black holes, in agreement with recent data from the Pierre Auger Observatory. Similarly, the ankle phenomenon at 3 EeV is shown to be explained by a split between inflational expansion and ordinary material expansion of the expanding heat bath, not unlike that in the expansion of the universe. All the spectral indicies in the respective regions of the energy spectra agree with the theoretical calculation from the respective expansion rates. It is shown that the ankle energy is approximately equal to the threshold energy of cosmic ray production of an electron positron pair on the cmb photon.
1. Introduction
There has been observational characteristics of cosmic ray energy spectrum on the discontinuity [1] at 3 PeV and at 3 EeV. The former is called the knee energy and the latter is called the ankle energy from the similarrity to the shape of the body structure. The spectral index of the former separates E−2.5 and E−3 spectra and those of the latter separates E−3 and E−2 spectra. There has been a proposal to explain the knee energy by a series of nuclear components of cosmic rays which respond to the galactic magnetic field, each having an anti-Gaussian energy spectrum at different peak positions [2]. This model is not only inconsistent with the observation of the nuclear components of cosmic rays below the knee energy [3], but it also requires the remainder of the energy spectrum to have a big hole near the knee energy and the totality of the energy spectrum to have a relatively simple shape, with spectral indicies of 2.5 and 3.0 below and above the knee energy of 3 PeV, respectively. It assumes too many accidental matchings of the intensities of the different mechanisms. It is desirable to have a unified mechanism which gives several spectral indices, so that the matching of intensities comes about naturally. Since 1985 the author has proposed such a model, which explains the knee energy phenomenon. In this model, the galactic components of cosmic rays which are created by supernova explosion, in particular, the nuclear components, are much smaller than the main component of the cosmic ray spectrum. This assumption is consistent with observational data for the nuclear components [3]. This article explains the ankle phenomenon from an inflational expansion, as a natural extension of the 1985 model.
2. The 1985 Model and Its Extension
In a series of articles [4-12] since 1985, the author has presented a model for the emission of high energy particles from AGN. The following is a summary of the model.
1) Quantum effects on gravity yield repulsive forces at short distances [4,6].
2) The collapse of black holes results in explosive bounce back motion with the emission of high energy particles.
3) Consideration of the Penrose diagram eliminates the horizon problem for black holes [7]. Black holes are not black any more.
4) The cause of supernova explosion after gravitational collapse of massive stars can be reduced to these repulsive forces.
5) The knee energy for high energy cosmic rays can be understood as a split between a radiation-dominated expansion and a matter-dominated expansion, not unlike that in the expansion of the universe. (See page 10 of the lecture notes [6] and the next section.)
6) Neutrinos and gamma rays as well as cosmic rays should have the same spectral index for each AGN, active galactic nucleus. They should show a knee energy phenomenon, a break in the energy spectral index at 3 PeV, similar to that for the cosmic ray energy spectrum.
It is worthwhile to mention that this model has been supported by recent data from the Pierre Auger Observatory [13], which has found a possible correlation between the sources of high energy cosmic rays and AGN.
Further discussion of the knee energy in the model yields the existence of a new mass scale in the knee energy range, in order to have the knee energy phenomenon in the cosmic ray spectrum [14]. The following are additional features of the model.
7) The proposed new particle with mass in the knee energy range (at 3 PeV) may not be stable, as in the case of the standard model. The standard model has particles at the 100 GeV mass scale, such as W and Z bosons, which are unstable. If it is a member of a supersymmetric multiplet and weakly interacting with ordinary particles, the stable particle of lowest mass becomes a candidate for a dark matter particle (DMP). The only requirement is that such particles must be present in AGN or black holes so that the knee energy phenomenon is observed when cosmic rays are emitted from AGN.
8) Using the supersymmetric theory of GLMR-RS (Giudice-Luty-Murayama-Rattazzi; Randall-Sundrum) [15, 16], the lowest mass corresponding to a knee energy mass of 3 PeV is 8.1 TeV. It is shown that the sum of 8 gamma ray observations from unknown sources in a HESS data [17] has a definite peak at 7.6 ± 0.1 TeV [18- 20].
9) There are several other particles with mass between 8 TeV and 3 PeV in the GLMR-RS theory.
We assume that the target mass range for the search is from 8 TeV to 3 Pev. In particular, the 3 PeV target is of prime importance, since it is a starting point for the discovery of a new mass scale. Moreover, it provides bases for matter-dominated expansion of black holes and possibly of the universe. It is expected that such particles are produced abundantly in the process of cosmic ray production from AGN as well as in the process of universe expansion. But most particles produced in AGN decay. They are produced in pairs in high energy cosmic ray showers and subsequently decay.
10) The production of a 3 PeV particle in the atmosphere requires the incident energy of cosmic rays or DMP at the GZK cutoff range [21,22]. The intensity is so small that one does not expect production in the atmosphere. The only possibility for such a particle is by a DMP target. With a heavy mass of 8 TeV for DMP, one can reduce the incident energy to 5.6 × 1017 eV, so that it has a higher intensity.
11) The measurement of a 3 PeV bump amounts to the measurement of the DMP distribution. From the muon energy spectrum one can get the DMP distribution in the 1012 cm range and from the neutrino energy spectrum one can get the DMP distribution for the whole galaxy. This provides an important tool for the study of dark matter physics [20].
One may call the proposed new particle at 3 PeV the Cion. This is an acronym for Cosmic Interface Particle. It is also taken from the Chinese word for knee, Xi (pronounced as shi).
3. Spectral Index and Expansion Rate
As described in the previous section, the model started from the realization that quantum effects on gravity yield a repulsive force at short distances. As a result, the collapse of a black hole proceeds to an explosion and an expanding heat bath emits various kinds of particles. This is the reason for the emission of high energy cosmic rays, gamma rays, neutrinos and DMP from black holes. The number of an emitted particle X with spin s is calculated by [4-6]
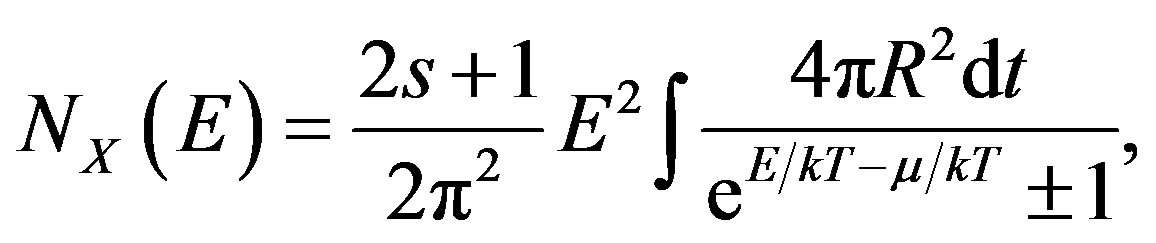 (1)
(1)
where R is the Radius of the heat bath with temperature T that emits particles and E2 is a phase space factor. The ± sign in the denominator is for fermions/bosons. With the assumption of the expansion rate
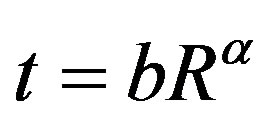 (2)
(2)
and
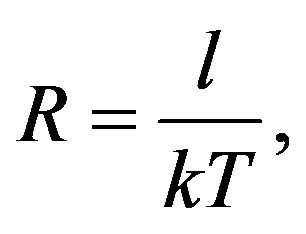 (3)
(3)
where b, l and 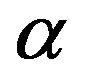 are constants, one can compute the number of particles
are constants, one can compute the number of particles
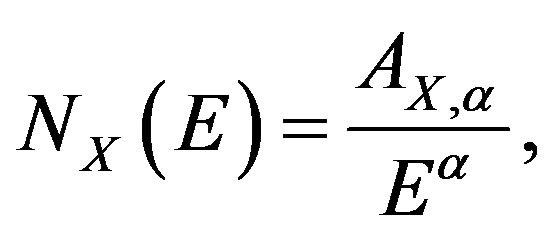 (4)
(4)
where
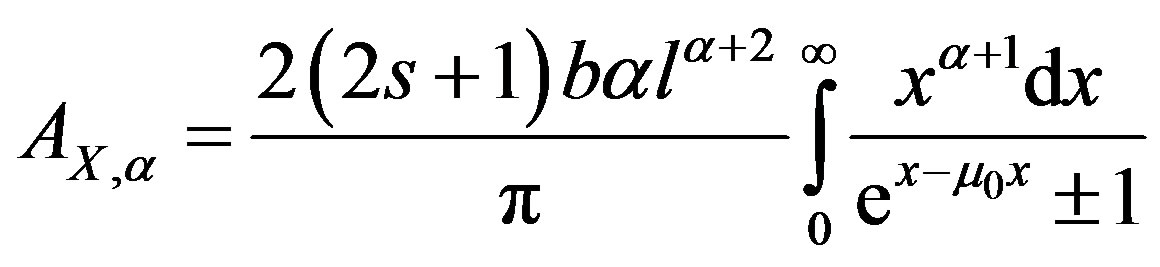 (5)
(5)
and
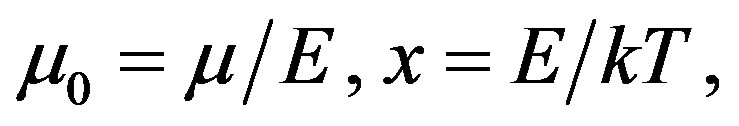 (6)
(6)
where 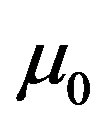 can be put to zero for high energy E.
can be put to zero for high energy E.
Then, the differential energy flux is given by
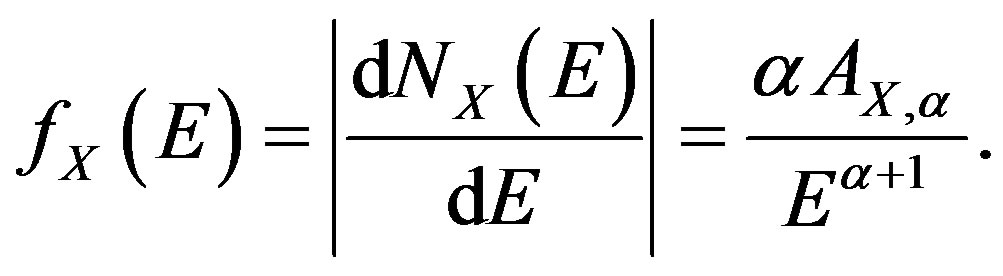 (7)
(7)
This is the energy spectrum of cosmic rays.
4. The Knee Energy and a New Mass Scale
From the expansion rate in cosmology, the exponent 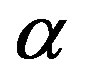 can be estimated as
can be estimated as
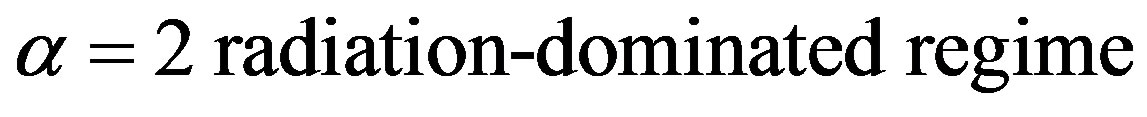 (8)
(8)
and
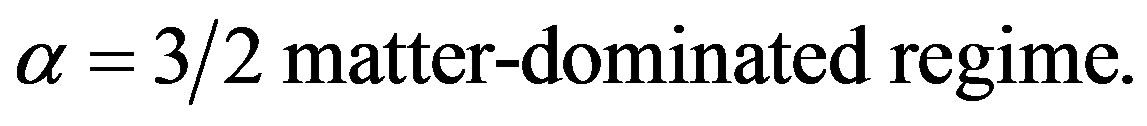 (9)
(9)
This gives the cosmic ray energy spectrum above the knee energy
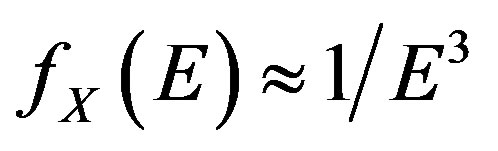 (10)
(10)
and below the knee energy
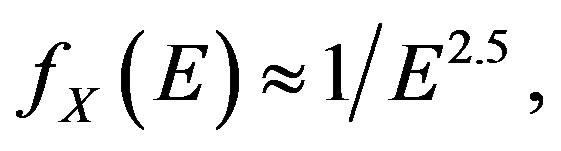 (11)
(11)
using Equation (7).
This is exactly the observed spectrum of cosmic rays. That is the explanation for the observed spectrum and the existence of the knee energy, proposed in my model in 1985 [4,12]. More recently, it was realized [14] that the model requires the existence of a mass scale at 3 PeV in order to produce the knee energy phenomenon at 3 PeV, since without it all ordinary particles behave as massless radiation at temperature 3 PeV. The existence of a new mass scale is the starting point for the discussion of a DMP and its family in the previous work [18-20].
5. The Ankle Phenomenon
The basic tenet of the 1985 model is a close connection between the expansion in cosmology and a heat bath expansion after gravitational collapse in a black hole. Then, it is quite natural to think that the material expansions (radiation-dominated and matter-dominated) are preceded by an inflational expansion. For an inflational expansion
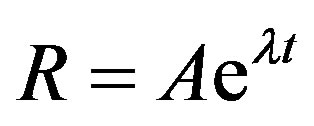 (12)
(12)
or
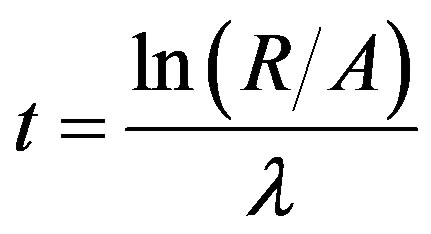 (13)
(13)
and then
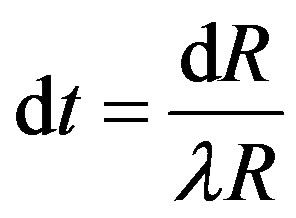 (14)
(14)
hence from Equation (7) one gets for 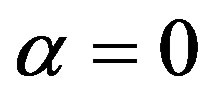
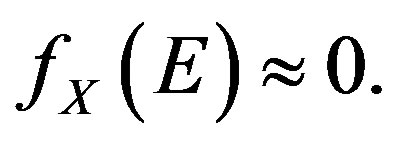 (15)
(15)
However, at higher energy E, a linear expansion dominates and hence
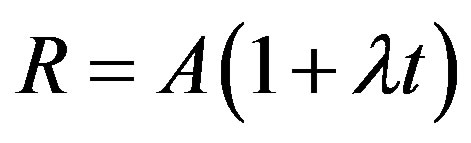 (16)
(16)
and for 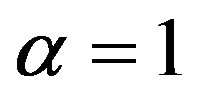 in Equation (7) one gets
in Equation (7) one gets
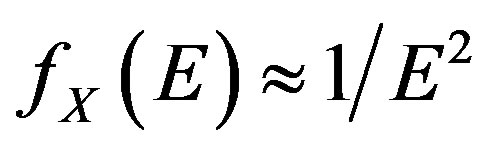 (17)
(17)
for high energy E. This is consistent with the observed spectrum above the ankle energy of 3 EeV.
For the expansion
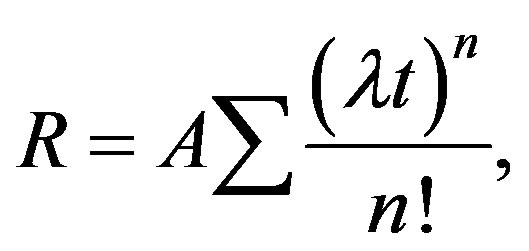 (18)
(18)
if
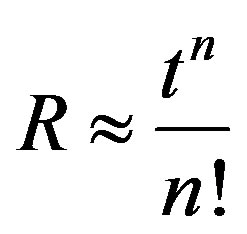 (19)
(19)
dominates, the spectrum becomes
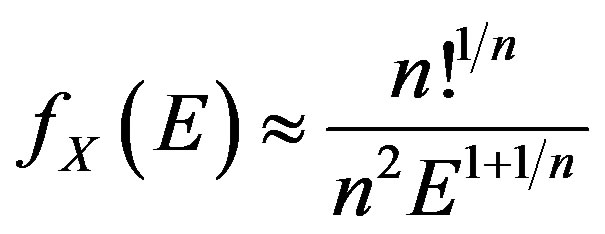 (20)
(20)
Since by Stirling formula
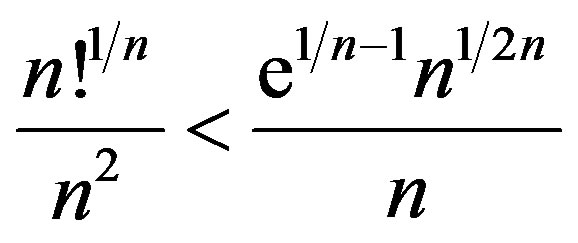 (21)
(21)
the right hand side of Equation (21) vanishes for large n, Equation (20) vanishes for large n. This explains the transition in the energy spectrum from 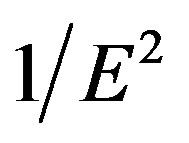 at high energy to 0 at low energy in the inflational expansion.
at high energy to 0 at low energy in the inflational expansion.
6. The Observed Spectral Indices near the Ankle Energy
The most recent determinations of spectral indices near the ankle energy for the cosmic ray spectrum are [23]
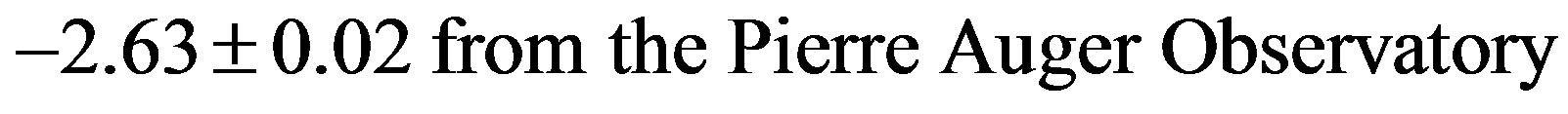 (22)
(22)
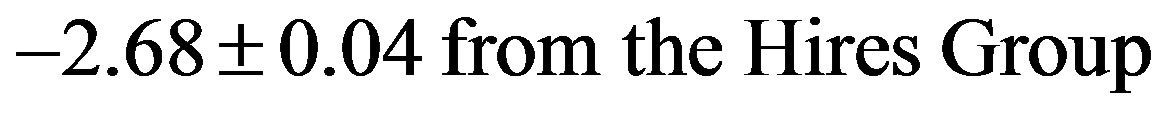 (23)
(23)
above the ankle energy, and
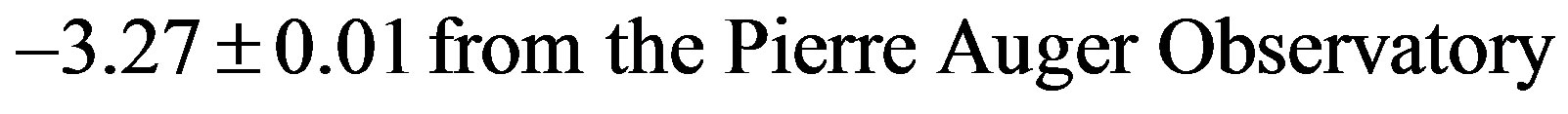 (24)
(24)
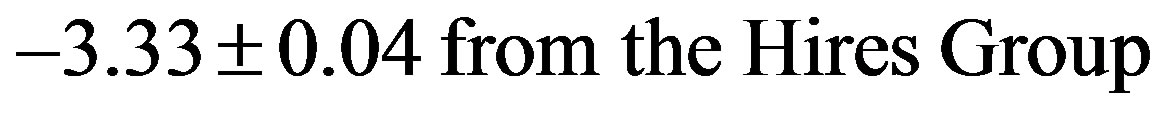 (25)
(25)
below the ankle energy. These values deviate from the predicted values of −2.0 and −3.0 respectively. These deviation may be the result of interactions of high energy cosmic rays with cmb (Cosmic Background Radiation) photons. In fact, such interactions caused the GZK cutoff above 1020 eV. Therefore, one may identify the theoretical prediction with the spectral indices for the energy spectra of neutrinos and DMP from AGN, where little interactions are expected with the cmb photons. Observation of the former is expected from the Ice-Cube and Anteras neutrino detectors in the near future.
An important question, then, is whether interactions between the high energy cosmic rays and the cmb photon can create the shifts in spectral indices
 (26)
(26)
above the ankle energy, and
 (27)
(27)
below the ankle energy. From a drastic change of the spectrum above the GZK cut-off energy, these shifts in the spectral indices seem to be conceivable, along with relative order of the change. It is important to resolve this question.
7. Cmb Photon Interactions
The GZK cut-off energy is obtained from the threshold of cosmic ray production of pion on a cmb photon,
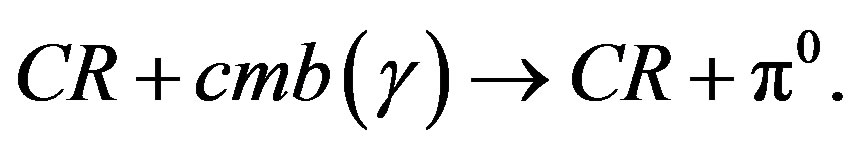 (28)
(28)
The energy equation for the lab frame and the cm frame at the threshold is given by
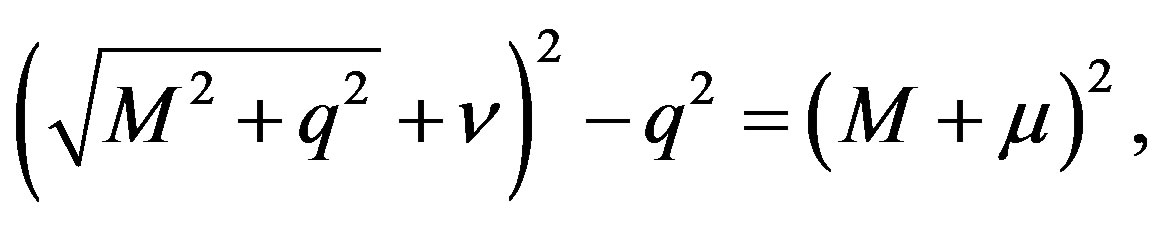 (29)
(29)
where 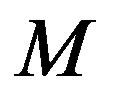 and
and 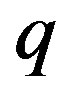 are the mass and momentum of cosmic rays and
are the mass and momentum of cosmic rays and 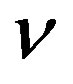 and
and 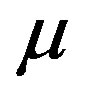 are the cmb photon energy and the mass of pion. The result is as follows:
are the cmb photon energy and the mass of pion. The result is as follows:
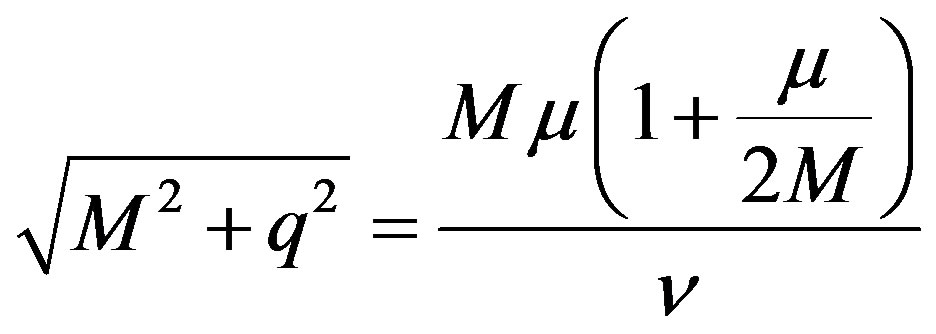 (30)
(30)
For
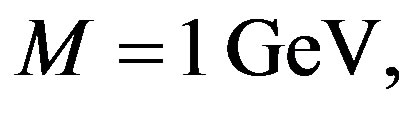 (31)
(31)
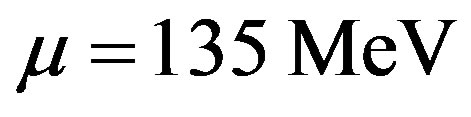 (32)
(32)
and
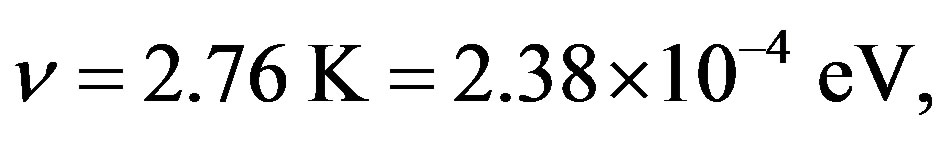 (33)
(33)
results in:
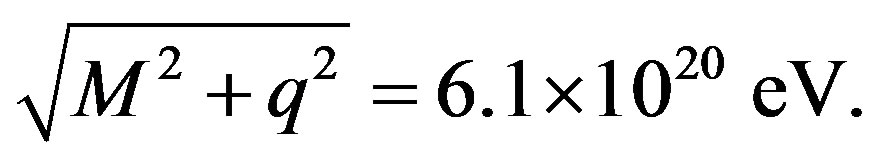 (34)
(34)
The result above is the estimate of the GZK cut-off energy. From Equation (30), the threshold energy is proportional to the mass of cosmic rays. The present observation of the GZK cut-off energy is consistent with protons being the dominant component of high energy cosmic rays. If the heavy mass components of cosmic rays are irons, the GZK cut-off energy would be much higher than what is observed.
The next process that needs to be considered for the interaction between cosmic rays and cmb photons is the pair production of electron and positron,
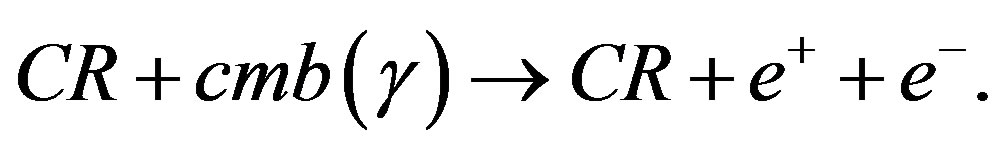 (35)
(35)
Using the mass of the pair
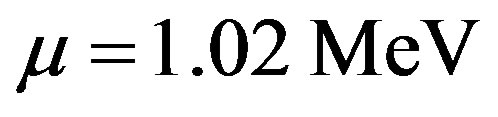 (36)
(36)
in Equation (30), one can generate a threshold energy for the reaction, Equation (35),
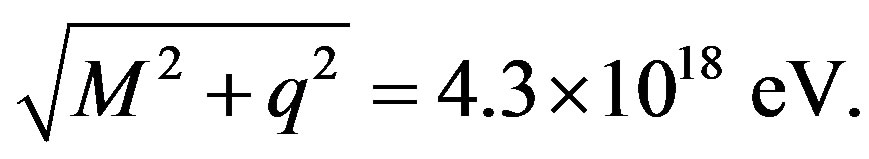 (37)
(37)
This result is approximately equal to the observed ankle energy. In other words, the ankle energy is nothing more than the threshold energy of cosmic ray production in an electron-positron pair by a cmb photon. Since this cross section is smaller than pion production by a factor of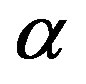 , the shift of the spectral index, Equation (26), by the pair production, Equation (35) results in a smaller probability. The change of the spectral index, Equation (26), is due to the loss of incident energy of cosmic rays. The effect is much less than that above the GZK cut-off energy due to a smaller cross section.
, the shift of the spectral index, Equation (26), by the pair production, Equation (35) results in a smaller probability. The change of the spectral index, Equation (26), is due to the loss of incident energy of cosmic rays. The effect is much less than that above the GZK cut-off energy due to a smaller cross section.
8. Connection between the Knee and the Ankle
This is nothing but the connection between the inflational expansion and the material expansion, which at best is yet to be clarified for the expansion of the universe [24]. The advantage in the cosmic ray energy spectrum is that it is directly observable so that any proposed model of inflation can be tested in the cosmic ray data to some extent. In conjunction with cosmological observations, one may hope to clarify the scenarios for inflation from the cosmic ray data, too, in the future.
The first question is what is the significance of the ankle energy of 3 EeV. This value is a reflection of the fractional contributions of the two expansions, inflational and material. The higher the contribution of the material relative to that of the inflational expansion, the higher the value of the ankle energy. From the existing cosmic ray energy data, one may discuss the following four cases for the connection between the two expansions.
1) Regional division of the two expansions One may assume that there is a divisional separation of the inflational expansion and the material expansion. In other words, while the outer region starts inflational expansion, the inner part continues material expansion.
2) Reheating after the inflational period This is a typical scenario after inflation in cosmology [24]. The temperature drops from inflational expansion can be reheated to a temperature above the knee energy (3 PeV). The outcomes of models I and II are similar. The only difference between the two is that a larger time lag between the arrival of cosmic rays above and below the ankle energy is required for II than for I. If the difference in arrival time can be measured statistically, then one may be able to differentiate the two models observationally.
3) Abortion of inflation after linear expansion Since the low energy extension of the cosmic ray energy spectrum for inflational expansion below the ankle energy is masked by that for material expansion, one may assume that the inflational expansion is terminated or aborted after a linear expansion. One has to inquire whether or not this is a possible theoretical scenario.
4) Separation of sources for inflational and material expansion Depending on the gravitational collapse conditions in the black hole, one may get dominance of either inflational or material expansion. In this case, one should observe a separation of the sources for the two types of expansion. One needs to observe the cosmic ray spectrum for a long period to separate the sources.
By clarifying various options for cosmic ray data which are discussed in this section, one may hope to find a link between cosmic ray physics and cosmology. Cases I, III and IV eliminate the necessity of reheating after inflation.
9. Summary
In the model proposed in 1985, the author has suggested that the knee energy is the split between radiationdominated expansion and matter-dominated expansion of an expanding heat bath of a black hole. This model predicted the recent data of the Pierre Auger Observatory on the correlation of high energy cosmic rays and the location of AGN. In this article, the author extended the 1985 model to incorporate the ankle energy as the split between radiation-dominated expansion and the linear expansion of the inflationay expansion. The value of the ankle energy indicates that the threshold value for cosmic rays producing e± pair by cmb photons is the meaning for the ankle energy. Thus, the model presented in 1985 and further extended in this paper explains the cosmic ray data that has been observed recently.
10. Acknowledgements
The author would like to thank David N. Williams and Peter K. Tomozawa for reading the manuscript.
REFERENCES
- A. Angelis, “The Mysteries of Cosmic Rays, Cern Courier,” 1999. http://www.physics.utah.edu/126whanlon/spectrum.html
- T. Wibig and A. W. Wolfendale, “Cosmic Ray Composition at the Ankle in the Energy Spectrum,” Astrophysics and Space Sciences Transactions, Vol. 7, 2011, pp. 275- 278. doi:10.5194/astra-7-275-2011
- M. Ichimura, et al., 29th International Cosmic Ray Conference, Vol. 101, 2005.
- Y. Tomozawa, “Magnetic Monopoles, Cosmic Rays and Quantum Gravity,” In: H. Terazawa and M. Yasue, Eds., Proceedings of INS International Symposium on Composite Models of Quarks and Leptons, Tokyo, 1985, p. 386.
- Y. Tomozawa, “The Origins of Cosmic Rays and Quantum Effects of Gravity,” In: F. Mancini, Ed., Quantum Field Theory, Ersever Science Publishers B. V., Amsterdam, 1986, p. 241.
- Y. Tomozawa, “Cosmic Rays, Quantum Effects on Gravity and Gravitational Collapse,” Second Workshop on Fundamental Physics, University of Puerto Rico, Humacao, 24-28 March 1986. http://www-lib.kek.jp/KISS/kiss_prepri.html
- Y. Tomozawa, “Gravitational Waves, Supernova and Quantum Gravity, in Symmetry in Nature,” Scuola Normale Superiore, Pisa, 1989, p. 779.
- Y. Tomozawa, “Exact Solution of the Quantum Einstein Equation and the Nature of Singularity,” In: D. Blair, et al., Eds., Proceedings of the 5th Marcel Grossman Meeting on General Relativity, Perth, 1988, p. 527.
- Y. Tomozawa, “Black Hole Oscillation,” In: D. Blair, et al., Eds., Proceedings of the 5th Marcel Grossman Meeting on General Relativity, Perth, 1988, p. 629.
- A. Majumdar and Y. Tomozawa, “Source Abundance of Cosmic Rays,” Progress of Theoretical Physics (Kyoto), Vol. 82, No. 3, 1989, pp. 555-562. doi:10.1143/PTP.82.555
- A. Majumdar and Y. Tomozawa, “Dynamical Behavior in Gravitational Collapse,” Nuovo Cimento, Vol. 197B, No. 8, 1992, pp. 923-939. doi:10.1007/BF02899295
- Y. Tomozawa, Astronomy and Astrophysics Supplement Series, Vol. 97, 1993, p. 117.
- The Pierre Auger Collaboration, “Correlation of the Highest-Energy Cosmic Rays with the Positions of Nearby Active Galactic Nuclei,” Science, Vol. 318, No. 5852, 2007, pp. 938-943. doi:10.1126/science.1151124
- Y. Tomozawa, “High Energy Cosmic Rays from AGN and the GZK Cutoff,” Modern Physics Letters A, Vol. 23, 2008, p. 1991.
- G. F. Giudice, M. A. Luty, H. Murayama and H. R. Rattazzi, Journal of High Energy Physics, Vol. 12, 1998, p. 027.
- L. Randall and R. Sundrum, “Out of This World Supersymmetry Breaking,” Nuclear Physics B, Vol. 557, No. 1-2, 1999, pp. 79-118. doi:10.1016/S0550-3213(99)00359-4
- F. Aharonian, et al., “HESS Very-High-Energy GammaRay Sources without Identified Counterparts,” Astronomy & Astrophysics, Vol. 477, No. 1, 2008, pp. 353-363. doi:10.1051/0004-6361:20078516
- Y. Tomozawa, “Evidence for a Dark Matter Particle,” 2010. arXiv:1002.1938.
- Y. Tomozawa, “Cosmic Rays from AGN, the Knee Energy Mass Scale and Dark Matter Particles,” 2010. srXiv:1002.1327
- Y. Tomozawa, “Search for a Dark Matter Particle Family,” 2012. arXiv:1207.2465
- K. Greisen, “End to the Cosmic-Ray Spectrum?” Physical Review Letters, Vol. 16, No. 7, 1966, pp. 748-750. doi:10.1103/PhysRevLett.16.748
- G. T. Zatsepin, V. A. Kuzmin and Z. Pisma, Journal of Experimental and Theoretical Physics, Vol. 4, 1966, p. 114.
- V. F. Hess, “100 Years Cosmic Rays—Anniversary of Their Discovery.” https://indico.desy.de/conferenceOtherViews.py?view=standard&confId=4213
- E. Kolb and M. S. Turner, “The Early Universe,” Addison-Wesley, Redwood City, 1990.

