Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21686,3 pages DOI:10.4236/jmp.2012.38101
The Exact Similarity between the Positron and the Electron Equations in a P and the T Violations
Université de Provence, Marseille, France
Email: boudet@cmi.univ-mrs.fr
Received May 23, 2012; revised June 18, 2012; accepted July 5, 2012
Keywords: Positron; the Electron Equations
ABSTRACT
Using in CPT a P and T violations we show that the equation of the positron is exactly the same as the one of the electron, on the condition that both the sign of the charge and the electromagnetic potential are changed. As a consequence the velocities are both in direction to the future and the masses are both positive and, in similar experiences, the behaviours of the two particles are the same. These theoretical results are in quite agreements with the experiments of the LEP.
1. An Invariant Form of the Dirac Equation
1.1. The Hestenes Form of the Dirac Equation
D. Hestenes has established in [1] a form of the Dirac equation of the electron in a galilean frame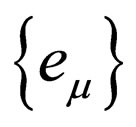 , by using the Clifford algebra
, by using the Clifford algebra  associated with the Minkowski space
associated with the Minkowski space , or Space-Time Algebra (STA) [2] (see Note below). This form eliminates the use of the complex Dirac matrices and spinor and replaces them in STA by a biquaternion
, or Space-Time Algebra (STA) [2] (see Note below). This form eliminates the use of the complex Dirac matrices and spinor and replaces them in STA by a biquaternion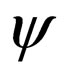 , element of
, element of  even sub-algebra of
even sub-algebra of , which expresses the wave function of the electron.
, which expresses the wave function of the electron.
The form given to  is the following
is the following
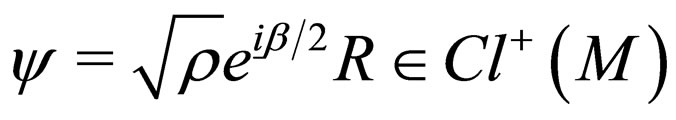 (1)
(1)
where:
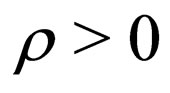 expresses the invariant probability density;
expresses the invariant probability density;
 ;
;
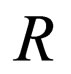 corresponds to the Lorentz rotation such that
corresponds to the Lorentz rotation such that 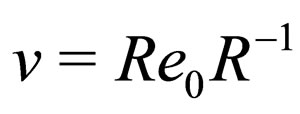 and
and  are the velocity and the invariant probability current;
are the velocity and the invariant probability current;
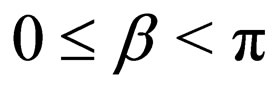 is the Yvon “angle” [3] (independently rediscovered by Hestenes [1]).
is the Yvon “angle” [3] (independently rediscovered by Hestenes [1]).
The vectors , are such that the bivectors
, are such that the bivectors 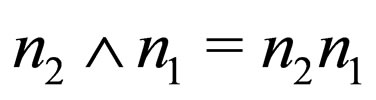 or
or  define, multiplied by
define, multiplied by , the angular momentum of the electron, in spin “up” or “down” respectively.
, the angular momentum of the electron, in spin “up” or “down” respectively.
Let us consider the Dirac equation
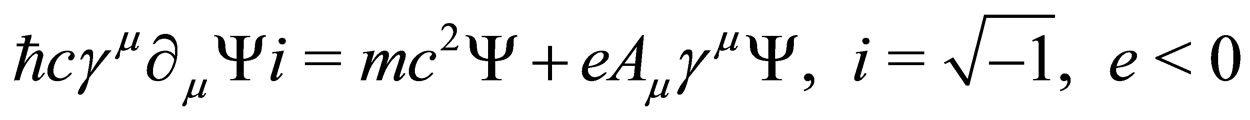 (2)
(2)
and the equivalences [1]

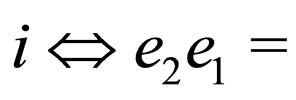 (in “up”),
(in “up”), 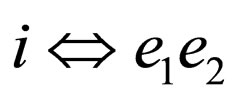 (in “down”),
(in “down”),
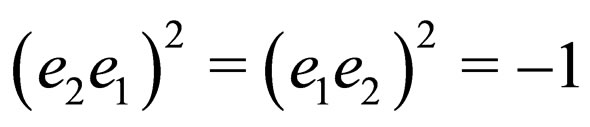 .
.
Denoting , one obtains the Hestenes form of the Dirac equation
, one obtains the Hestenes form of the Dirac equation
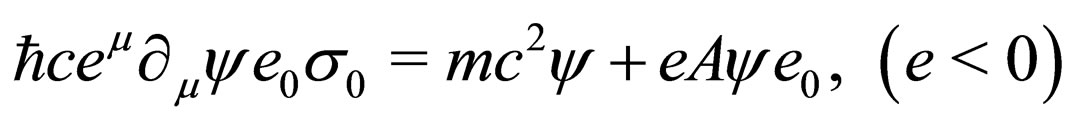 (3)
(3)
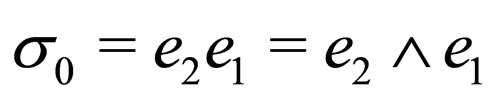 in “up”,
in “up”, 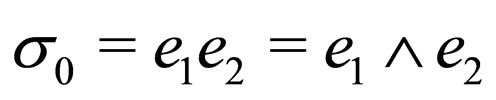 in “down”
in “down”
1.2. An Invariant Form of the Hestenes Equation
Multiplying Equation (2) on the right by  (
(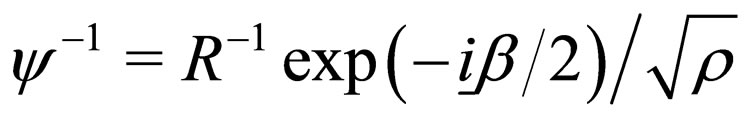 ), we obtain [4]
), we obtain [4]
 (4)
(4)

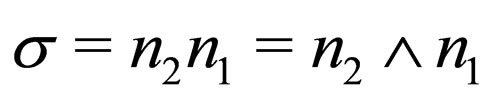 in “up”,
in “up”,  in “down”, where the bivectors
in “down”, where the bivectors  define the infinitesimal rotation of the moving frame
define the infinitesimal rotation of the moving frame , or proper frame of the electron.
, or proper frame of the electron.
This equation is independent with respect to all galilean frame. The dimension of each term is an energy. In this form the velocity v is associated with  and gives the equation of the free electron, considered when the potential A is null. So this form appears as the most appropriated among the other invariant forms.
and gives the equation of the free electron, considered when the potential A is null. So this form appears as the most appropriated among the other invariant forms.
Note: The Clifford algebra 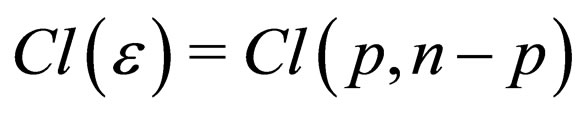 associated with an euclidean space
associated with an euclidean space 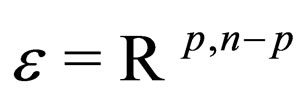 is a real associative algebra, generated by
is a real associative algebra, generated by  and the vectors of
and the vectors of , whose elements are identified to the ones of the Grassmann algebra
, whose elements are identified to the ones of the Grassmann algebra . Furthermore this algebra implies the use of the inner products in
. Furthermore this algebra implies the use of the inner products in  denoted
denoted ,
,  for products of a p-vector
for products of a p-vector  by a vector a of
by a vector a of  which correspond to the operation so-called (by the physicists) “contraction on the indices”. The product
which correspond to the operation so-called (by the physicists) “contraction on the indices”. The product  (
( ) defines the signature
) defines the signature  of
of . Its principal properties are:
. Its principal properties are:
1) The Clifford product of two elements 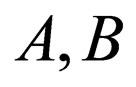 of
of 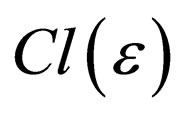 is denoted AB and verifies the fundamental relation
is denoted AB and verifies the fundamental relation .
.
2) All element A of is the sum of terms in the form
 ,
, .
.
3) .
.
4) If p vectors 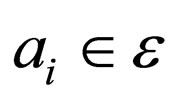 are orthogonal their Clifford product verifies
are orthogonal their Clifford product verifies .
.
2. The P and T Violations
2.1. The CPT Transforms
We recall the usual presentation of the passage from the equation of the electron to the one of the positron by means of the CPT transforms that we apply to Equation (4).
1) C (Charge) changes 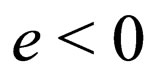 into
into .
.
2) P (Parity) changes  into
into  and so
and so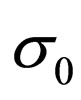 ,
,  into
into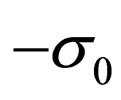 ,
,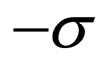 .
.
3) T (Time reversion) changes 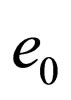 into
into 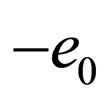 and so
and so  in
in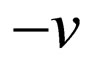 .
.
Equation (4) becomes, after the change of sign of  and v, associated with the C change,
and v, associated with the C change,
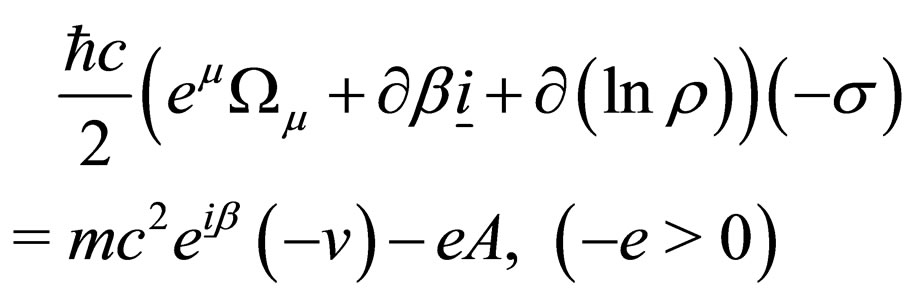 (5)
(5)
However the T transformation seems to imply that the positrons come from the future, contrarily to experiments in particular in the LEP, and these kinds of transformations are to be imperatively interpreted in a different way.
2.2. Theoretical Justification of a P and the T Violations
Note that the changes of sign of  and
and 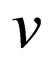 are made to put the terms containing the spin and the velocity in agreement with the change of sign of the term containing the charge.
are made to put the terms containing the spin and the velocity in agreement with the change of sign of the term containing the charge.
So one has not to change by P  into
into 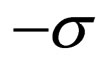 but, instead, to keep
but, instead, to keep  unchanged and to change the sign of the term of the equation containing the spin, and so not to change the spin.
unchanged and to change the sign of the term of the equation containing the spin, and so not to change the spin.
In the same way one has not to change by the T transform v into 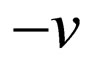 but, instead, to keep v unchanged and to change the sign of the term of the equation containing v, and so not to change the velocity v.
but, instead, to keep v unchanged and to change the sign of the term of the equation containing v, and so not to change the velocity v.
So the positron velocity may be clearly considered in direction to the future and the strange interpretation of T by Stückelberg and Feymann is to be abandoned.
Equation (5) is changed into
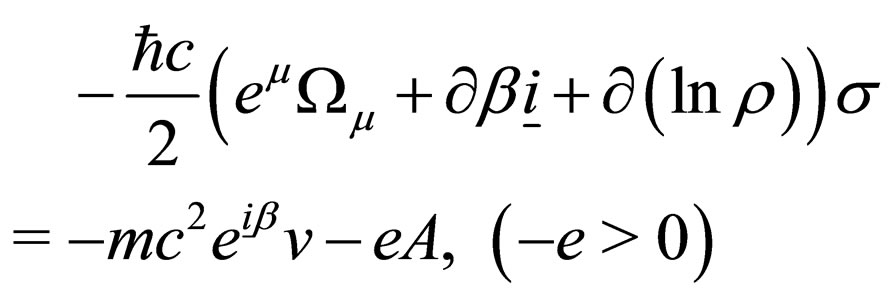 (6)
(6)
that is
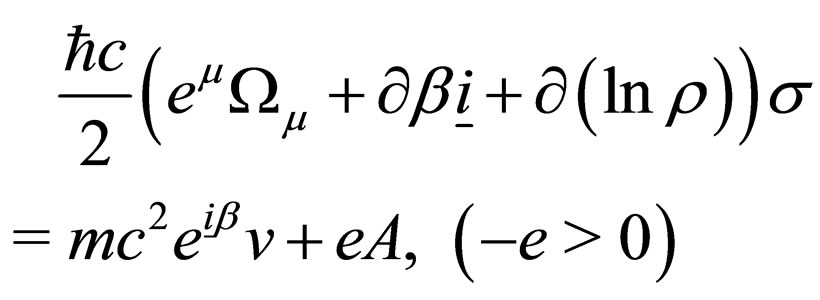 (7)
(7)
This equation is exactly the same as the equation of the electron, with the condition that, the charge 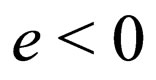 being changed into
being changed into , one has to change the electromagnetic potential A acting on the electron in
, one has to change the electromagnetic potential A acting on the electron in  acting on the positron:
acting on the positron: .
.
2.3. The CP-Takabayasi Transform
In [5], Equation (10.3b), T. Takabayasi avoids the change of v into  by the following transform:
by the following transform:
3)' The angle  is changed into
is changed into 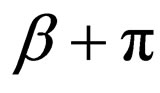 which gives
which gives
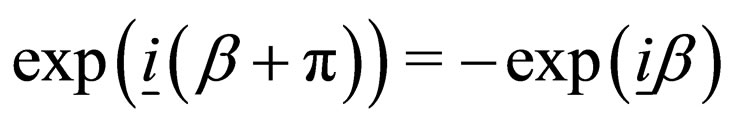 , v remaining unchanged.
, v remaining unchanged.
A difference with what precedes is the fact the sign minus is placed directly in front of the term containing the mass and so that T may be removed from CPT to be replaced by the above transform on the “angle” .
.
About the spin the addition of  to the “angle”
to the “angle” , which in fact concerns not the vectors of M but the bivectors (see for example [6], p. 37), may change a bivector
, which in fact concerns not the vectors of M but the bivectors (see for example [6], p. 37), may change a bivector 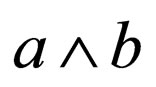 into
into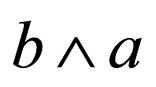 . This addition of
. This addition of  to
to 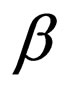 is coherent with P which nevertheless needs to be violated as it is explained above.
is coherent with P which nevertheless needs to be violated as it is explained above.
Note that Takabayasi had assigned the sign minus obtained by his transform to the mass, not to the term containing the mass, and deduced a wrong hypothesis of a negative mass for the positron (that we have unluckily repeated in [6], p. 37).
3. Conclusions
About the behaviour of the positron in the LEP experiments we have sent to Michel Spiro, President of Scientific Board of the LEP, then of the LHC, the following message:
“The form of the positron equation is the same as the electron equation, except that the charge is positive. So one can expect that, in similar experiences, the behaviour of the positron ought to be the same as the one of the electron to the condition that the sign of the electromagnetic potential A is changed.”
We have received the following answer (which does not engage its author on the validity of the above calculations) from Dr. Rolf Landua, Head of Education and Public Outreach (CERN):
“I can confirm that this statement is correct. It has also undergone many experimental tests, e.g. by testing the equality of the magnetic moment of the electron and the positron. This measurement is hitherto the most precise comparison of a physical property of particle and antiparticle.”
REFERENCES
- D. Hestenes, “Space-Time Algebra” Gordon and Breach, New York, 1966.
- D. Hestenes, “Real Spinor Fields,” Journal of Mathematical Physics, Vol. 8, No. 4, 1967, pp. 798-808. doi:10.1063/1.1705279
- J. Yvon, “Equations of Dirac-Madelung,” Journal de Physique et le Radium, Vol. 1, No. 1, 1940, pp. 18-24. doi:10.1051/jphysrad:019400010101800
- R. Boudet, “Sun Une Forme Intrinseque de i’Equation de Dirac et Son Interpretation Geometrique,” Compte Rendus de l’Académie des Sciences, Vol. 71, 1971, p. 104.
- T. Takakbayasi, “Relativistic Hydrodynamics of the Dirac Matter,” Progress of Theoretical Physics Supplement, No. 4, 1957, pp. 1-4.
- R. Boudet, “Quantum Mechanics in the Geometry of Space-Time—Elementary Theory,” Springer-Verlag, Heidelberg, 2011. doi:10.1007/978-3-642-19199-2

