Journal of Modern Physics
Vol. 2 No. 10 (2011) , Article ID: 8097 , 22 pages DOI:10.4236/jmp.2011.210149
Mass Spectrum in the Minimal Supersymmetric 3-3-1 Model
Universidade Federal do Rio Grande-FURG, Instituto de Matemática, Estatística e Física-IMEF, Rio Grande, RS, Brazil
E-mail: marcosrodriguez@furg.br
Received May 18, 2011; revised July 5, 2011; accepted July 2011
Keywords: Supersymmetric Models
ABSTRACT
We consider the minimal supersymmetric extension of the 3-3-1 model. We study the mass spectrum of this model in the fermionic and gauge bosons sectors without the antisextet. We also present some phenomenological consequences of this model at colliders such as Large Hadron Collider (LHC) and International Linear Collider (ILC).
1. Introduction
The models based on the 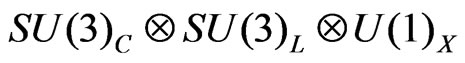 (called 3-3-1 models) [1-7]. In fact, this may be the last symmetry involving the lightest elementary particles: leptons. The lepton sector is exactly the same as in the Standard Model (SM) but now there is a symmetry, at large energies among, say
(called 3-3-1 models) [1-7]. In fact, this may be the last symmetry involving the lightest elementary particles: leptons. The lepton sector is exactly the same as in the Standard Model (SM) but now there is a symmetry, at large energies among, say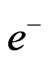 ,
, 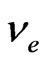 and
and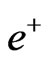 . Once this symmetry is imposed on the lightest generation and extended to the other leptonic generations it follows that the quark sector must be enlarged by considering exotic charged quarks. It means that some gauge bosons carry lepton and baryon quantum number. Although this model coincides at low energies with the SM it explains some fundamental questions that are accommodated, but not explained, in the SM as the generation number problem (The family number must be a multiple of three in order to cancel anomalies [1-7]), why
. Once this symmetry is imposed on the lightest generation and extended to the other leptonic generations it follows that the quark sector must be enlarged by considering exotic charged quarks. It means that some gauge bosons carry lepton and baryon quantum number. Although this model coincides at low energies with the SM it explains some fundamental questions that are accommodated, but not explained, in the SM as the generation number problem (The family number must be a multiple of three in order to cancel anomalies [1-7]), why 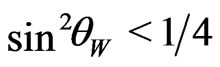 is observed, the electric charge quantization [8], etc).
is observed, the electric charge quantization [8], etc).
Since one generation of quarks is treated differently from the others this may lead to a natural explanation for the large mass of the top quark [9]. There is also a good candidate for Self Iinteracting Dark Matter (SIDM) since there are two Higgs bosons, one scalar and one pseudoscalar, which have the properties of candidates for dark matter like stability, neutrality and that it must not overpopulate the universe [10], etc.
There are two main versions of the 3-3-1 models depending on the embedding of the charge operator in the 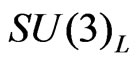 generators,
generators,
 (1)
(1)
where the ![]() parameter defines two different representation contents,
parameter defines two different representation contents,  denotes the
denotes the  charge and
charge and ,
, 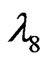 are the diagonal generators of
are the diagonal generators of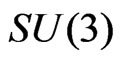 . In the minimal version, with
. In the minimal version, with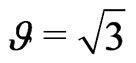 , the charge conjugation of the right-handed charged lepton for each generation is combined with the usual
, the charge conjugation of the right-handed charged lepton for each generation is combined with the usual 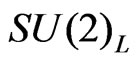 doublet left-handed leptons components to form an
doublet left-handed leptons components to form an  triplet
triplet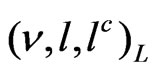 . No extra leptons are needed in the mentioned model, and we shall call such model as minimal 3-3-1 model. There are also another possibility where the triplet
. No extra leptons are needed in the mentioned model, and we shall call such model as minimal 3-3-1 model. There are also another possibility where the triplet 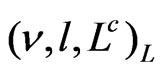 where
where ![]() is an extra charged leptons wchich do not mix with the known leptons [11]. We want to remind that there is no right-handed (RH) neutrino in both model. There exists another interesting possibility, where (
is an extra charged leptons wchich do not mix with the known leptons [11]. We want to remind that there is no right-handed (RH) neutrino in both model. There exists another interesting possibility, where ( ) a left-handed anti-neutrino to each usual
) a left-handed anti-neutrino to each usual  doublet is added to form an
doublet is added to form an  triplet
triplet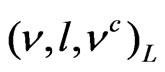 , and this model is called the 3-3-1 model with RH neutrinos. The 3-3-1 models have been studied extensively over the last decade.
, and this model is called the 3-3-1 model with RH neutrinos. The 3-3-1 models have been studied extensively over the last decade.
The supersymmetric version of the minimal 3-3-1 model was done at Refs. [12-15] (MSUSY331) while the version with right-handed neutrinos [4-7] has already been constructed at Ref. [16,17] (SUSY331RN), while the Supersymmetric economical 3-3-1 model with RH has been presented recently [18] (SUSYECO331).
Recently we have constructed all the spectrum from the scalar sector from the MSUSY331 model [19]. All the results obtained on that article are in agreement with the experimental bounds.
This paper is organized as follows. In Section 2 we review the minimal supersymmetric 331 model while in Section 4 we show how we can define one 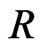 -parity in our model such way that the neutrinos can get their masses and keeping the proton and the neutron stability. While in Sections 3 and 5 we present some phenomenological consequences of this model to the colliders physics. While on Section 6 we present the masses values of all the fermions and gauge bosons of this model. Finally, the last section is devoted to our conclusions. In Appendix 8 we present the Lagrangian of this model in terms of the fields.
-parity in our model such way that the neutrinos can get their masses and keeping the proton and the neutron stability. While in Sections 3 and 5 we present some phenomenological consequences of this model to the colliders physics. While on Section 6 we present the masses values of all the fermions and gauge bosons of this model. Finally, the last section is devoted to our conclusions. In Appendix 8 we present the Lagrangian of this model in terms of the fields.
2. Minimal Supersymmetric 3-3-1 Model (MSUSY331)
On this Section, we present our model. We start to introduce the minimal set of particle necessary to build the supersymmetric version of model given at Ref. [11]. After the introduction of the particle content of our model we put them in the superfields, see Subsection 2.2, and then we construct the full Lagrangian of this model in Subsection 2.3. Then we show the pattern of the symmetry breaking at Subsection 2.4.
2.1. Particle Content
In the nonsupersymmetric 3-3-1 model [2,3] the fermionic representation content is as follows: lefthanded leptons (In parenthesis it appears the transformations properties under the respective factors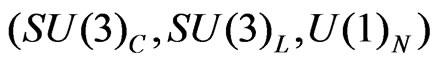 )
) ,
, ; left-handed quarks
; left-handed quarks
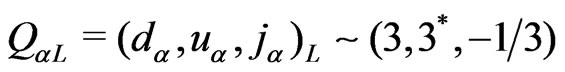 ,
, 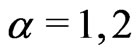 ,
,
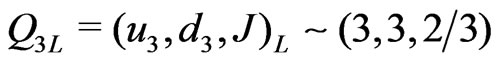 ;
;
and in the right-handed components we have the usual quarks

 , and the exotic quarks
, and the exotic quarks
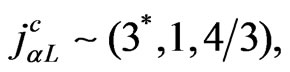 , these exotic quarks have charge
, these exotic quarks have charge 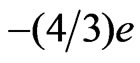 and
and  respectivelly. The minimal scalar representation content is formed by three scalar triplets:
respectivelly. The minimal scalar representation content is formed by three scalar triplets:
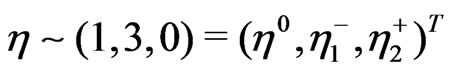
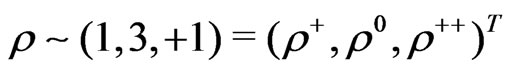
and
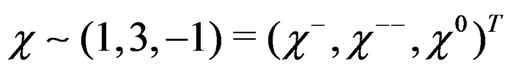 .
.
Now, we introduce the minimal set of particles in order to implement the supersymmetry [20]. We have to introduce the sleptons the superpartners of the leptons and the squarks related to the quarks, both are scalars. Therefore in the supersymmetric version of this model [12-15], the fermionic content is the same as in the nonsupersymmetric 331 model and we have to add their supersymmetric partners ,
, 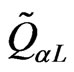 ,
,  ,
, 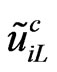 ,
,  ,
, 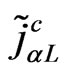 and
and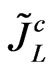 . We have also to introduce the higgsinos the supersymmetric partner of the scalars of the model and the minimal higgsinos are given by
. We have also to introduce the higgsinos the supersymmetric partner of the scalars of the model and the minimal higgsinos are given by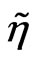 ,
,  and
and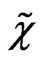 . However, we have to introduce, the followings extras scalars
. However, we have to introduce, the followings extras scalars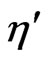 ,
,  ,
,  and their higgsinos
and their higgsinos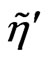 ,
,  and
and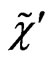 , in order to to cancel chiral anomalies generated by
, in order to to cancel chiral anomalies generated by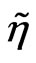 ,
, 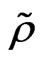 and
and .
.
In the gauge sector we introduce the usual gauge bosons of the symmetries, it means the gluons by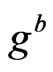 , the gauge boson of
, the gauge boson of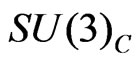 ;
; , with
, with  the gauge boson of
the gauge boson of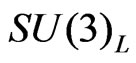 ; and the gauge boson of
; and the gauge boson of  symmetry denoted as
symmetry denoted as . Now, we introduce their supersymetric partners: the gluinos, are denoted by
. Now, we introduce their supersymetric partners: the gluinos, are denoted by , the gauginos of
, the gauginos of 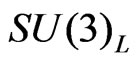 symmetry given by
symmetry given by ; and
; and 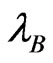 the gaugino of the last group.
the gaugino of the last group.
In the nonsupersymmetric 3-3-1 model to give arbitrary mass to the leptons we have to introduce one scalar antisextet representation, given by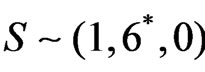 . We can avoid the introduction of the antisextet by adding a charged lepton transforming as a singlet. Notwithstanding, here we will omit both the antisextet and the singlet. We are going to show in Sec.6 all the fermions and gauge bosons get their masses only with three triplets and three antitriplets in agreement with [21].
. We can avoid the introduction of the antisextet by adding a charged lepton transforming as a singlet. Notwithstanding, here we will omit both the antisextet and the singlet. We are going to show in Sec.6 all the fermions and gauge bosons get their masses only with three triplets and three antitriplets in agreement with [21].
This is the minimal number of fields in the minimal supersymmetric extension of the 3-3-1 model of Refs. [12-15]. Summaryzing, we have in the 3-3-1 supersymmetric model the following superfields: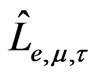 ,
, 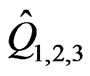 ,
, 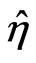 ,
, 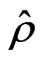 ,
,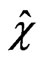 ;
;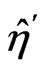 ,
,  ,
, ;
;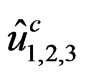 ,
,  ,
, ![]() and
and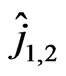 , i.e., 21 chiral superfields, and 17 vector superfields:
, i.e., 21 chiral superfields, and 17 vector superfields: 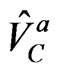 (
( ),
),  (
( ) and
) and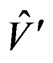 . In the Minimal Supersymmetric Standard Model (MSSM) [20,22-30] there are 14 chiral superfields and 12 vector superfields.
. In the Minimal Supersymmetric Standard Model (MSSM) [20,22-30] there are 14 chiral superfields and 12 vector superfields.
2.2. Superfields
The superfields formalism is useful in writing the Lagrangian which is manifestly invariant under the supersymmetric transformations [31] with fermions and scalars put in chiral superfields while the gauge bosons in vector superfields. As usual the superfield of a field  will be denoted by
will be denoted by 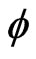 [20]. The chiral superfield of a multiplet
[20]. The chiral superfield of a multiplet  is denoted by [31]
is denoted by [31]
 (2)
(2)
while the vector superfield is given by
 (3)
(3)
The fields  and
and 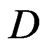 are auxiliary fields which are needed to close the supersymmetric algebra and eventually will be eliminated using their motion equations.
are auxiliary fields which are needed to close the supersymmetric algebra and eventually will be eliminated using their motion equations.
2.3. The Lagrangian
On this subsection we will write only the lagrangian in the terms of superfields of the model. The Lagrangian of the model has the following form
 (4)
(4)
where 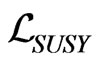 is the supersymmetric part and
is the supersymmetric part and  the soft terms breaking explicitly the supersymmetry.
the soft terms breaking explicitly the supersymmetry.
The supersymmetric term can be divided as follows
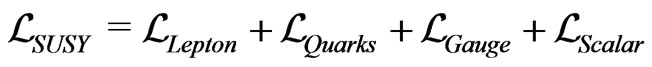 (5)
(5)
The fermion’s lagrangian is given by [12-15]
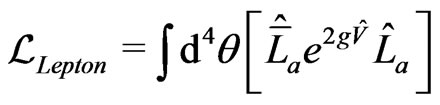
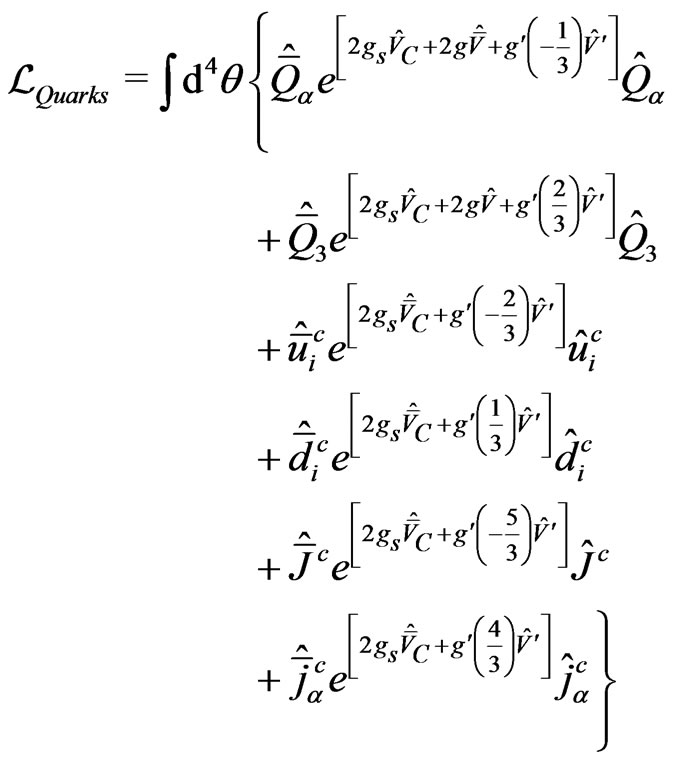 (6)
(6)
where we have defined ,
, ;
;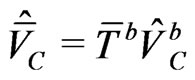 ,
, ;
; ,
,  are the generators of triplet and antitriplets representations, respectively, and
are the generators of triplet and antitriplets representations, respectively, and  are the Gell-Mann matrices.
are the Gell-Mann matrices.
In the gauge sector we have
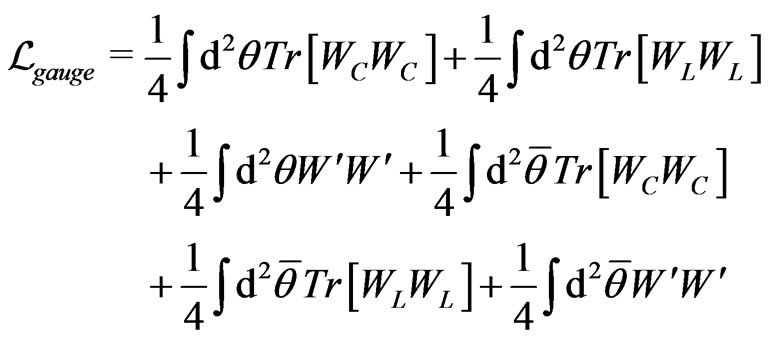 (7)
(7)
where ,
,  e
e 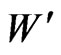 are fields that can be written as follows [31]
are fields that can be written as follows [31]

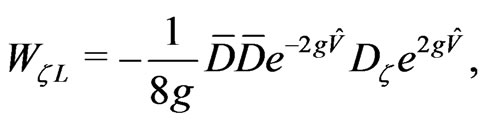
 (8)
(8)
Finally, in the scalar sector we have
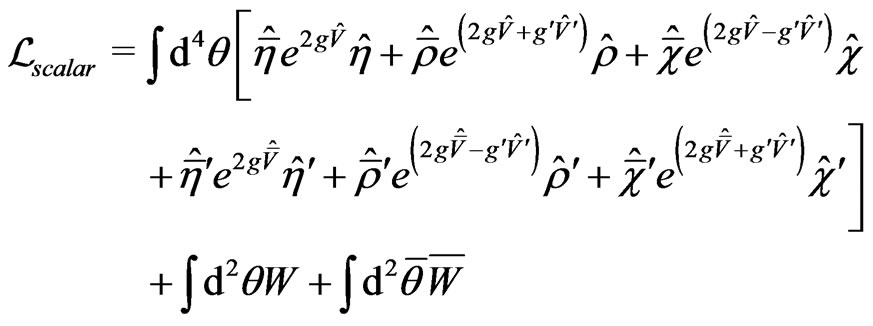 (9)
(9)
where ![]() and
and 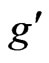 are the gauge coupling constants of
are the gauge coupling constants of 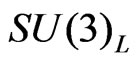 and
and 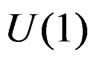 respectivelly and
respectivelly and 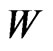 is the superpotential of the model.
is the superpotential of the model.
The superpotential of our model is given by
 (10)
(10)
with 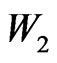 having only two chiral superfields while
having only two chiral superfields while 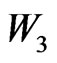 has three chiral superfields. The most general terms allowed by our symmetry are
has three chiral superfields. The most general terms allowed by our symmetry are
 ,
,
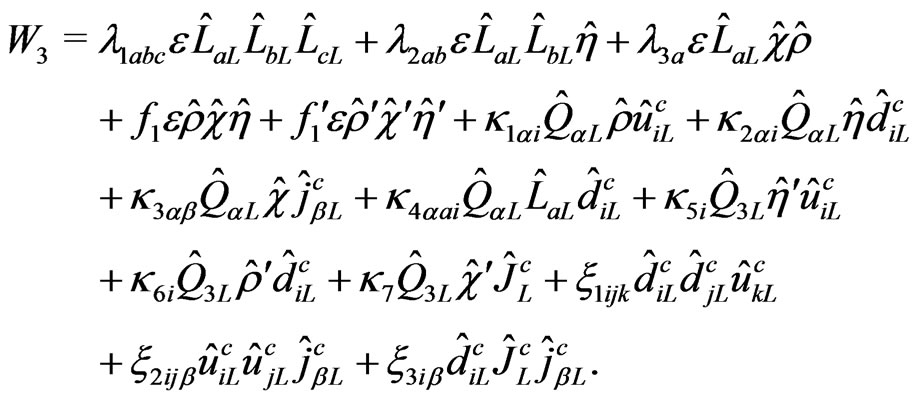 (11)
(11)
The coefficients 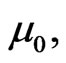
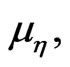
 and
and 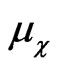 have mass dimension, while all the coefficients in
have mass dimension, while all the coefficients in 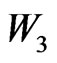 are dimensionless [29,30].
are dimensionless [29,30].
The most general soft supersymmetry breaking terms, which do not induce quadratic divergence, were described by Girardello and Grisaru [32]. They found that the most general terms that break supersymmetry (SUSY) can be categorized as:
• scalar mass term
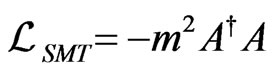 (12)
(12)
• gaugino mass term
 (13)
(13)
• scalar interaction terms
 (14)
(14)
They, also, must be consistent with the 3-3-1 gauge symmetry. These soft terms are given by
 (15)
(15)
where
 (16)
(16)
due this term the gauginos get theis masses at scale where SUSY is broken while their superpartners the gauge bosons are massless, for more detail about symmetry breaking in this model see Subsection 2.4. The second term give masses to the sleptons, squarks and usual scalars is written as
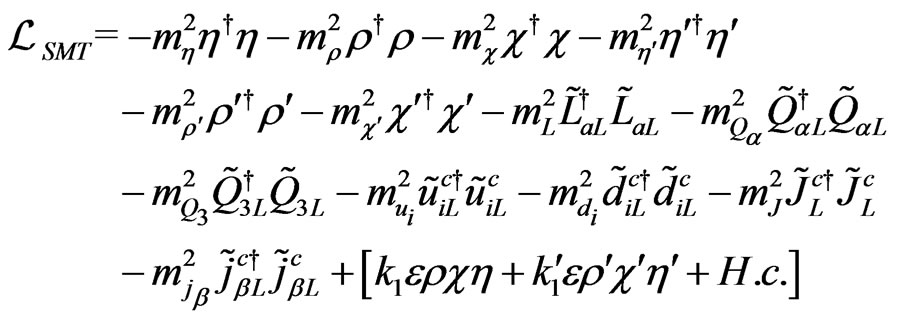 (17)
(17)
while the last term is given by
 (18)
(18)
2.4. Breake Structure from MSUSY331 to 
The pattern of the symmetry breaking of the model is given by the following scheme(using the notation given at [2,3,12-15])
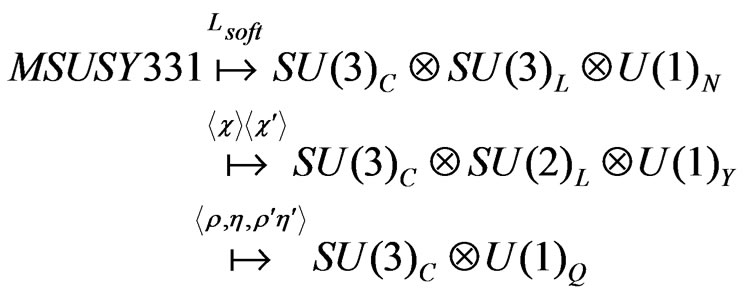 (19)
(19)
When we breaks the symmetries of our model, the scalars get the following vacuum expectation values (VEVs):

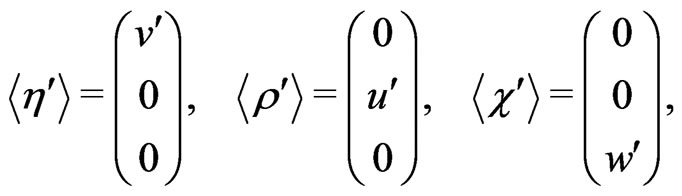 (20)
(20)
where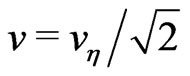 ,
,  ,
,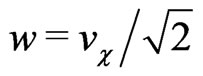 ,
,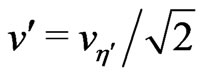 ,
,  and
and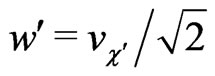 . From this pattern of the symmetry breaking comes the following constraint [15]
. From this pattern of the symmetry breaking comes the following constraint [15]
 (21)
(21)
coming from , where, we have defined
, where, we have defined 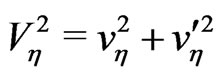 and
and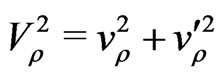 . Therefore the VEV’s of our model satisfy the conditions:
. Therefore the VEV’s of our model satisfy the conditions:
 . (22)
. (22)
3. Phenomenological Consequences in the Lepton’s and Quark’s Sectors
In the usual 3-3-1 model the physical gauge bosons are defined as [2,3]

 ,
,

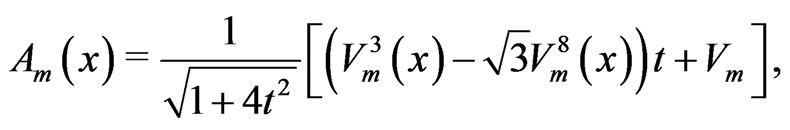

 (23)
(23)
where 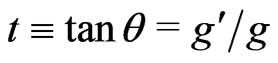 and
and 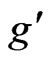 and
and ![]() are the gauge coupling constants of
are the gauge coupling constants of 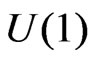 and
and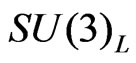 , respectively.
, respectively.
The bosons 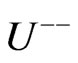 and
and  are called bileptons because they couple to two leptons. The charged current interactions for the fermions, came from
are called bileptons because they couple to two leptons. The charged current interactions for the fermions, came from ![]() (first equation at Equation (121)) and from
(first equation at Equation (121)) and from  (first equation at Equation (122)) we can rewrite them in the following way
(first equation at Equation (122)) we can rewrite them in the following way

 (24)
(24)
where we have defined the mass eigenstates in the following way

 , (25)
, (25)
and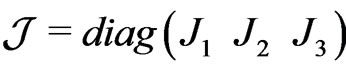 . The
. The  is the usual CabibboKobayashi-Maskawa mixing matrix, while
is the usual CabibboKobayashi-Maskawa mixing matrix, while  is the Pontecorvo-Maki-Nakagawa-Sakata mixing matrix in the neutrino sector. The new mixing matrices
is the Pontecorvo-Maki-Nakagawa-Sakata mixing matrix in the neutrino sector. The new mixing matrices 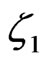 and
and  containing new unknown mixing parameters due to the presence of the exotic quarks.
containing new unknown mixing parameters due to the presence of the exotic quarks.
The gauge bosons  and
and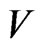 , both, have two units of lepton number, it means
, both, have two units of lepton number, it means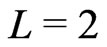 . Here
. Here ![]() is the total lepton number, give by
is the total lepton number, give by . This model does not conserve separate family lepton number,
. This model does not conserve separate family lepton number,  ,
,  and
and 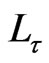 but only the total lepton number
but only the total lepton number ![]() is conserved.
is conserved.
We can define the charged gauginos, in analogy with the gauge bosons in the MSSM, in the following way [15]

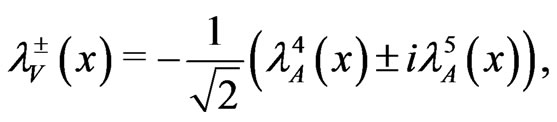
 .(26)
.(26)
We can calculate the Higgs couplings to the usual leptons on this model, it is given by![]() , see Equation (129) at Appendix 8. We get the following lagrangian [2,3]
, see Equation (129) at Appendix 8. We get the following lagrangian [2,3]
 (27)
(27)
the coupling 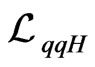 is
is
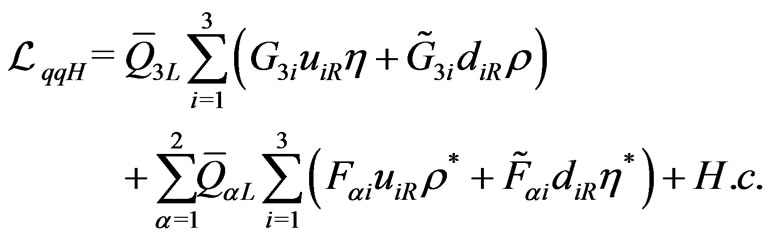 (28)
(28)
In this model leptons with same flavor don’t couple with the neutral Higgs, therefore our lighest Higgs doesn’t couples with two electrons1 and of course it can decay in the following way , and their coupling is
, and their coupling is , see [21], due this fact our light Higgs with
, see [21], due this fact our light Higgs with ![]() GeV was not detected [19] by the experiment Large Electron Positron (LEP).
GeV was not detected [19] by the experiment Large Electron Positron (LEP).
We have already showed that in the Mø ller scattering and in muon-muon scattering we can show that left-right asymmetries  are very sensitive to a doubly charged vector bilepton resonance but they are insensitive to scalar ones [33-35].
are very sensitive to a doubly charged vector bilepton resonance but they are insensitive to scalar ones [33-35].
Similarly, we have the neutral currents coupled to both  and
and  massive vector bosons, according to the Lagrangian
massive vector bosons, according to the Lagrangian
 (29)
(29)
with , for neutrinos and
, for neutrinos and
 (30)
(30)
for the charged leptons, where we have defined
We can use muon collider to discover the new neutral  boson using the reaction
boson using the reaction  it was shown at [34,36] that
it was shown at [34,36] that  asymmetry is considerably enhanced.
asymmetry is considerably enhanced.
The Lagrangian interaction among quarks and the 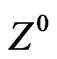 is
is
 (31)
(31)
where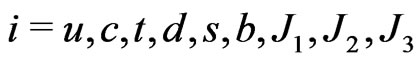 ; with
; with
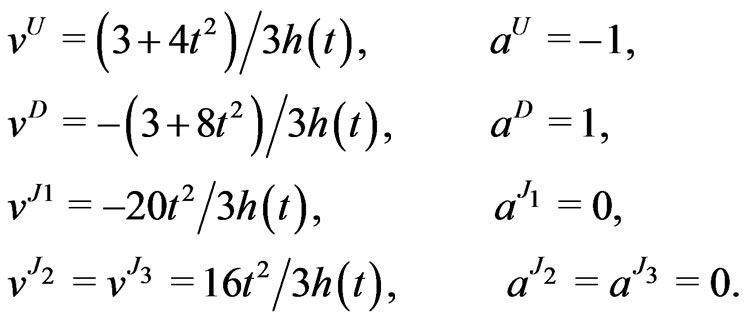
There is also the usual QCD Lagrangian given by
 (32)
(32)
the lagrangians presented at Equations (24), (29-32) are the same as appear in the 331 model [2,3]. In those lagrangians appear a lot of interestings phenomenologiacal studies presented at [37-40].
We can, also, study the following process resulting in at least three leptons coming from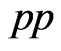 collision, throught the following reactions2
collision, throught the following reactions2

 (33)
(33)
For example the first process has the following Feynmann diagrams drawing in Figures 1, 2. Similar diagrams can be drawn to the process 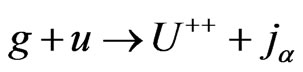 (change
(change  and
and ).
).
As first results, in Figure 3 we present the differencial cross section, get from the program COMPHEP [41], to the process  as function of
as function of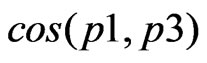 . We can conclude from this figure that the pair
. We can conclude from this figure that the pair  will be produce in a dominant way in the forward direction, in the backward direction we get small differencial cross section.
will be produce in a dominant way in the forward direction, in the backward direction we get small differencial cross section.

Figure 1.  exchanging quark-
exchanging quark-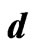 .
.

Figure 2. 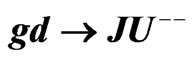 exchanging quark-
exchanging quark-![]() .
.
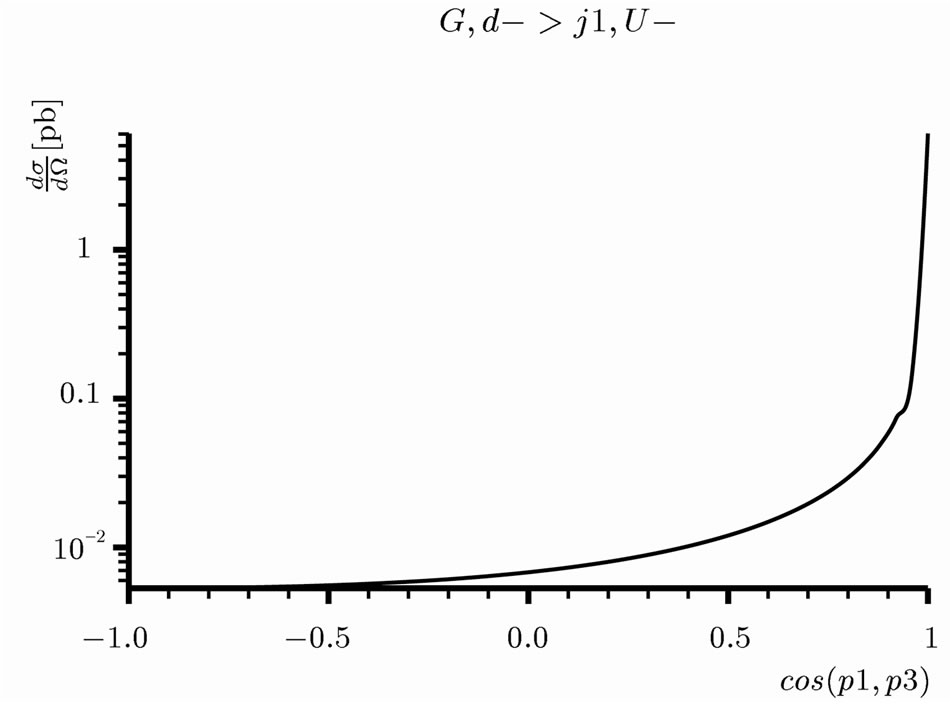
Figure 3. Differential Cross Section .
.
We have also calculated the cross section to these process as function of  and
and  and our results are shown in Figure 4(a) and Figure 4(b) respectively. In Figures 5(a)(b) we present the results on forwardbaskward asymmetry as function of
and our results are shown in Figure 4(a) and Figure 4(b) respectively. In Figures 5(a)(b) we present the results on forwardbaskward asymmetry as function of 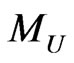 (
(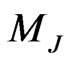 ) respectivelly. Similar results can also be get to the process
) respectivelly. Similar results can also be get to the process .
.
In Figures 4, 5(a) we fixed 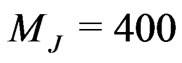 GeV and in this case we get bigger total cross section and forward-
GeV and in this case we get bigger total cross section and forward-
 (a)
(a) (b)
(b)
Figure 4. Total Cross Section  as function of
as function of 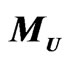 (a) and
(a) and 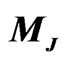 (b).
(b).
 (a)
(a) (b)
(b)
Figure 5. Asymmetry 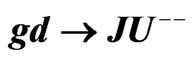 as function of
as function of  (a) and
(a) and  (b).
(b).
baskward asymmetry if the 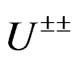 boson mass is lower than
boson mass is lower than  GeV. In the right figures we fixed
GeV. In the right figures we fixed 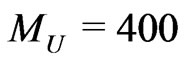 GeV and near
GeV and near  GeV we get minimal point to both the cross section and forwardbackward asymmetry to other values of
GeV we get minimal point to both the cross section and forwardbackward asymmetry to other values of 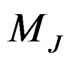 we get bigger values than in this case.
we get bigger values than in this case.
From Equation (32), the new gauge bosons can decay in the followings channels 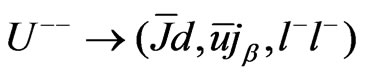 and
and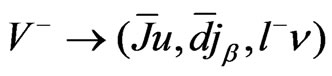 . These decays modes are shown in Figure 6. The heavy quarks
. These decays modes are shown in Figure 6. The heavy quarks![]() ,
,  and
and  can decay to the light quark via
can decay to the light quark via 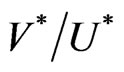 emission to produce bilepton final states with a specific decay signature, see Figure 7.
emission to produce bilepton final states with a specific decay signature, see Figure 7.
We can conclude, from the Figures 6, 7, that the ![]() quark will decay mainly in
quark will decay mainly in  or
or 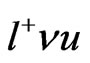 modes without any restrictions coming from the new bosons gauge masses, because these particles are virtual on this decay. While the
modes without any restrictions coming from the new bosons gauge masses, because these particles are virtual on this decay. While the  quark can decay in
quark can decay in 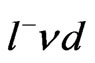 and
and .
.
By another hand, the  decay will depend of
decay will depend of 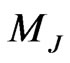 and
and  masses. We show in Table 1 all possibles decays modes to this gauge boson.
masses. We show in Table 1 all possibles decays modes to this gauge boson.
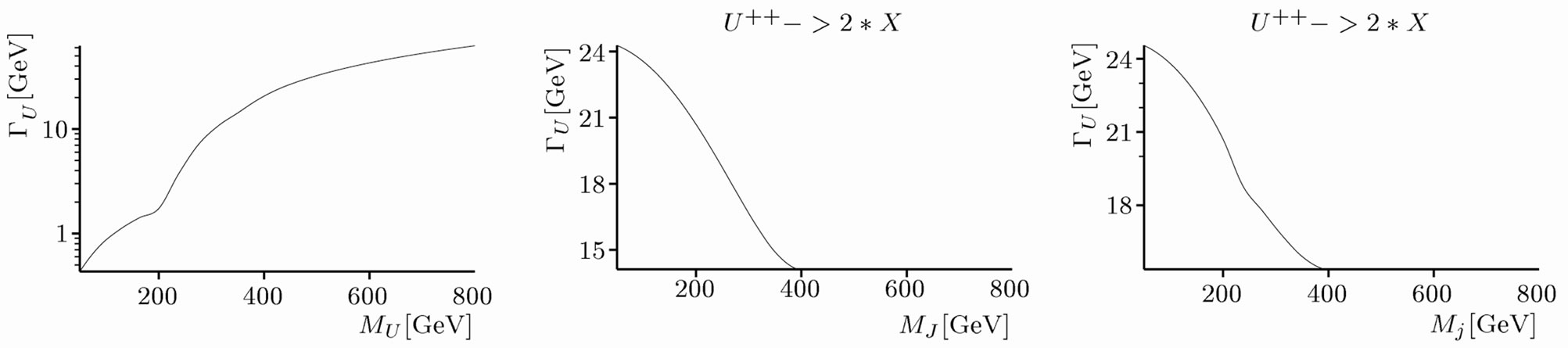
The width of the 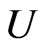 boson is drawing in the Figure 8(a) as function of its mass. We see in this figure that the
boson is drawing in the Figure 8(a) as function of its mass. We see in this figure that the

Figure 6. U and V decay in two particles.
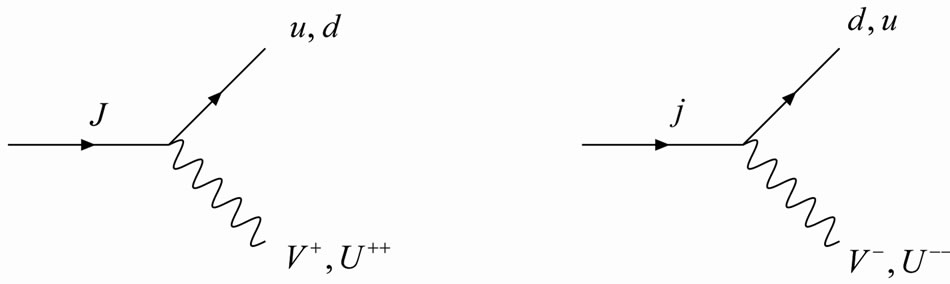
Figure 7. J and j decay in ordinary quarks and bileptons that will decay too.
width increase with the mass until  GeV when it become constant. In Figure 8(b) we draw
GeV when it become constant. In Figure 8(b) we draw 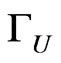 versus
versus , while in Figure 8(c) we plot
, while in Figure 8(c) we plot 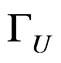 versus
versus 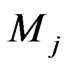 where we have fixed
where we have fixed 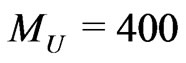 GeV.
GeV.
We also present the width of the  boson versus its mass in Figure 9(a) as function of its mass. In Figure 9(b)
boson versus its mass in Figure 9(a) as function of its mass. In Figure 9(b) 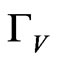 versus
versus 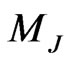 is shown, while in Figure 8(c) we plot
is shown, while in Figure 8(c) we plot 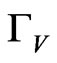 versus
versus . The behavior of these plots are simlar of the
. The behavior of these plots are simlar of the  boson.
boson.
We can see that the main signal to the channel we have analysed is . Of course three processes, given at Equation (33), must be better studied but from our analyse we can say the experimental signal from these proces is the three lepton production. We know that this kind of signal can be detected at Large Hadron Collider (LHC) if they really exist in nature.
. Of course three processes, given at Equation (33), must be better studied but from our analyse we can say the experimental signal from these proces is the three lepton production. We know that this kind of signal can be detected at Large Hadron Collider (LHC) if they really exist in nature.
There are background come mainly from the SM and from MSSM [29,30]. The background from the SM comes from the ,
,  ,
, 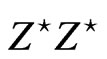 and
and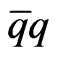 . The
. The

Table 1. All possibles decays to the U boson.

Table 2. States coming from JU– – decay.
 (a) (b) (c)
(a) (b) (c)
Figure 8. U decay width as function of  (a),
(a),  (b) and
(b) and  (c).
(c).
 (a) (b) (c)
(a) (b) (c)
Figure 9. V decay width as function of  (a),
(a), 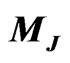 (b) and
(b) and  (c).
(c).
 and
and 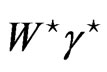 background are known to be the major source of background come from the SM, where we have the following decays
background are known to be the major source of background come from the SM, where we have the following decays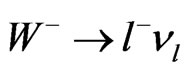 ,
,  and
and , for the three lepton channel. The second largest background font to three leptons channel is from
, for the three lepton channel. The second largest background font to three leptons channel is from  events. Finally, the remaining three leptons background which should worry about is the
events. Finally, the remaining three leptons background which should worry about is the 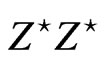 jet production.
jet production.
In the MSSM the charginos, neutralinos, gluinos and squarks pair production leads to a trilepton signature too. The trilepton final states that could arise from the decay of charginos 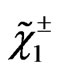 and neutralinos
and neutralinos . For the reaction
. For the reaction , where
, where 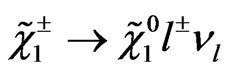 and
and , and
, and 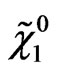 is the LSP. The
is the LSP. The 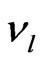 and two LSPs do not interact and manifest themselves as missing energy. The resulting final states is three isolated charged leptons plus missing energy. While the squarks
and two LSPs do not interact and manifest themselves as missing energy. The resulting final states is three isolated charged leptons plus missing energy. While the squarks 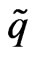 and the gluinos
and the gluinos ![]() have the following interactions
have the following interactions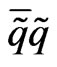 ,
,  and
and 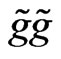 and the decays of squarks and gluinos are
and the decays of squarks and gluinos are 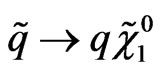 and
and 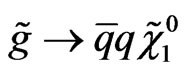 [28-30].
[28-30].
To finish this analyses from interactions of gauge bosons, we can study 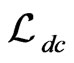 given at Equation (126) at Appendix 8. From this lagrangian we can derive the following Feynman rules given the trilinear and quartic coupling. On this case we get the same results presented [42,43], given at Table 3. Here the following notations were used
given at Equation (126) at Appendix 8. From this lagrangian we can derive the following Feynman rules given the trilinear and quartic coupling. On this case we get the same results presented [42,43], given at Table 3. Here the following notations were used

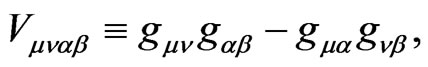
 (34)
(34)
4. R-Parity
The R-symmetry was introduced in 1975 by A. Salam and J. Strathdee [44] and P. Fayet [22] to avoid the interactions that violate either lepton number (L) or baryon number (B) conservation. There is very nice review about this subject in Refs. [45,46]. More precisely, R-parity can be written as
 (35)
(35)
where ![]() is the spin of the particle.
is the spin of the particle.
We said above that only the total lepton number, ![]() , remains a global quantum number (or equivalently we can define
, remains a global quantum number (or equivalently we can define  as the global conserved quantum number where B is the baryonic number [11]). However, if we assume the global
as the global conserved quantum number where B is the baryonic number [11]). However, if we assume the global  symmetry, it allows us to introduce the
symmetry, it allows us to introduce the  -conserving symmetry, defined as
-conserving symmetry, defined as
 . The
. The  number attribution is
number attribution is


Table 3. Trilinear and Quartic couplings in the MSUSY331.
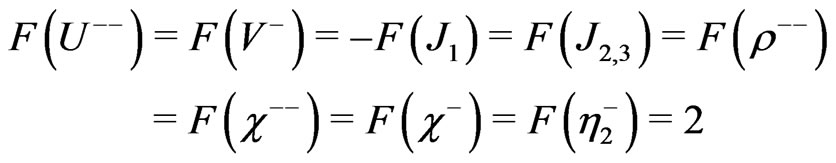 (36)
(36)
with  for the other Higgs scalar, while for leptons and the known quarks
for the other Higgs scalar, while for leptons and the known quarks  coincides with the total lepton and baryon numbers, respectively.
coincides with the total lepton and baryon numbers, respectively.
Choosing the following R-charges
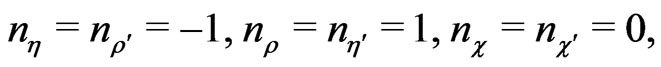
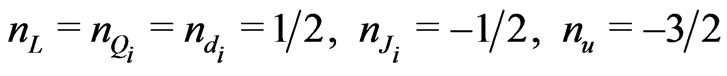 (37)
(37)
it is easy to see that all the fields ,
,  ,
, 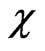 ,
, 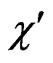 ,
, 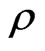 ,
,  ,
, ![]() ,
,  ,
, ![]() ,
, ![]() and
and 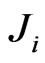 have R-charge equal to one, while their superpartners have opposite R-charge similar to the MSSM. The terms which satisfy the defined above symmetry (37) are given by
have R-charge equal to one, while their superpartners have opposite R-charge similar to the MSSM. The terms which satisfy the defined above symmetry (37) are given by
 (38)
(38)
In this case only the quarks get masses. However not all of the leptons get mass. This is because the Yukawa coupling 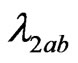 is only non-zero when it is antisymmetric in the generation indices (
is only non-zero when it is antisymmetric in the generation indices (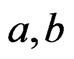 ). In the usual 331 model to generate the charged lepton masses we have to introduce an antisextet, as we don't introduce this scalar in our model the charged leptons are massless in this case. The neutrinos are also massless.
). In the usual 331 model to generate the charged lepton masses we have to introduce an antisextet, as we don't introduce this scalar in our model the charged leptons are massless in this case. The neutrinos are also massless.
However, if we want to allow neutrinos to get their masses and at the same time avoid the fast nucleon decay we can choose the following  -charges
-charges
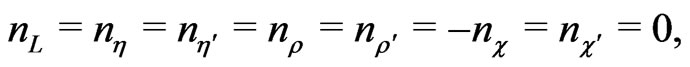
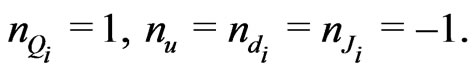 (39)
(39)
In this case, the terms allow in our superpotential are
 (40)
(40)
In our superpotential, we can generate mass to neutrinos, as we will show in the next section. We maintain the proton stability at tree-level [12-14]. However it is not enough to forbid the dangerous processes of nucleon decay. Fortunatelly our super-potential forbid the neutron-antineutron oscillation, see Refs. [29,30,45- 47].
The last term in this superpotential induce the following nice process [29,30,45]
1) Double Beta Decay without Neutrinos 2) New contributions to the Neutrals 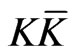 and also
and also  Systems;
Systems;
3) An additional contribution to the muon decay;
4) Charged Current Universality in ![]() and
and ![]() decays;
decays;
5) Charged Current Universality in the Quark Sector;
6) Leptonic Decays of Heavy Quarks Hadrons such as
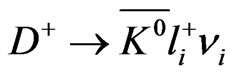 ;
;
7) Rare Leptonic Decays of Mesons like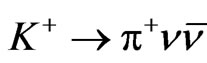 8) Hadronic
8) Hadronic  Meson Decay Asymmetries.
Meson Decay Asymmetries.
it also give the following direct decays of the lightest neutralinos
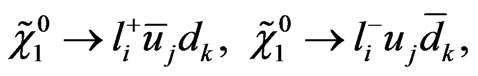
 (41)
(41)
and for lightest charginos

 (42)
(42)
These very nice aspects also is hold in SUSY331RN and in SUSYECO331 models [48].
5. Chargino and Neutralino Production
However, on this model we have doubly charged vector bosons and scalars, respectivelly. This means that in some supersymmetric extensions of these kind of models we will have double charged charginos [15,49,50]. On this model the charginos can decay in the following way
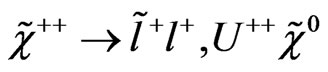 ,
,
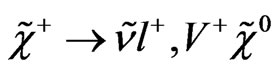 ,
,
 . (43)
. (43)
Possible two body modes decays of sleptons are
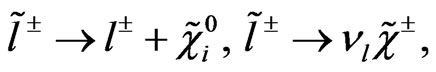
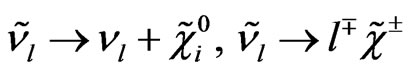 . (44)
. (44)
In a previous work [15,49,50] we have have calculated the total cross section to the reactions
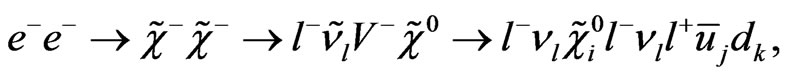
 .(45)
.(45)
we know that the ILC will start to run with  TeV and therefore this detector can detect them if they really exist in nature.
TeV and therefore this detector can detect them if they really exist in nature.
Take this information into account we can say that
 .(46)
.(46)
Again another interesting signal that can be measured at the International Linear Collider (ILC).
Naturally these particles can also be detected at LHC through, in a similar way as described above, throught the processes
 ,
,
 (47)
(47)
and on this case we thinks it will be intersting to study these process to the LHC.
6. Mass Spectrum
Here in this article, we want to present the mass spectrum of the Minimal Supersymmetric 3-3-1 model. We will present first the results in the fermionic sector, then in the bosonic sector.
6.1. Leptons Masses
In a previous work we have shown that, in the MSUSY331, we don’t need to use the antisextet to generate the masses to the leptons.
Let us first considered the charged lepton masses. Denoting
 (48)
(48)
where all the fermionic fields are still Weyl spinors, we can also, as before, define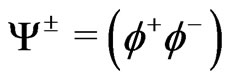 , and the mass term
, and the mass term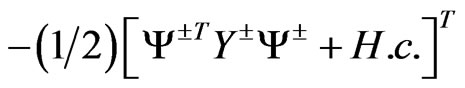 where
where  is given by:
is given by:
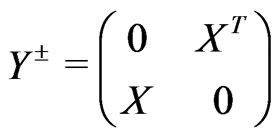 (49)
(49)
with Equation (50)
 (50)
(50)
where we have defined  and
and 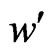 at Equation (20).
at Equation (20).
The chargino mass matrix  is diagonalized using two unitary matrices,
is diagonalized using two unitary matrices, 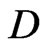 and
and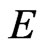 , defined by
, defined by
 (51)
(51)
( and
and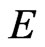 sometimes are denoted, in non-supersymmetric theories, by
sometimes are denoted, in non-supersymmetric theories, by 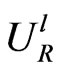 and
and , respectively). Then we can write the diagonal mass matrix as
, respectively). Then we can write the diagonal mass matrix as
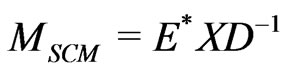 (52)
(52)
To determine  and
and , we note that
, we note that
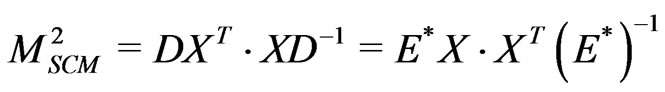 (53)
(53)
and define the following Dirac spinors:
 (54)
(54)
where  is the particle and
is the particle and  is the anti-particle.
is the anti-particle.
We will use the following values for the dimensionless parameters
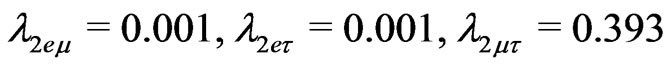 ,
,
 (55)
(55)
 (56)
(56)
and for the mass dimension parameters (in GeV) we have used:
 (57)
(57)
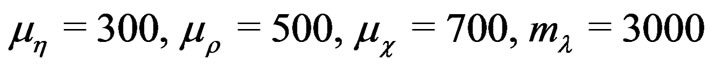 (58)
(58)
We also use the constraint 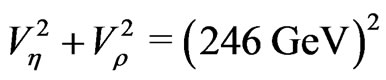 coming from
coming from , where, we have defined
, where, we have defined  and
and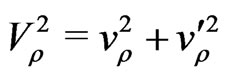 . Assuming that
. Assuming that
 (59)
(59)
the value of  is fixed by the constraint above.
is fixed by the constraint above.
We have obtained, considerating Equations (55)-(59), the following masses (in GeV) for the charged sector:
![]() ,
,
![]() , (60)
, (60)
and the masses for the usual leptons (in GeV) ,
,  and
and .
.
We can say from the values presented above that we can detect at ILC or LHC several charginos (since 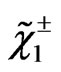 until at least
until at least ) using the processes given at Equations (43),(45).
) using the processes given at Equations (43),(45).
Notice, from Equation (60), that the electron is massless at the tree level. This is a result of the structure of the mass matrix in Equation (50) and there is not a symmetry that protects the electron to get a mass by loop corrections. We obtain that the dominant contribution to the electron mass is, up to logarithmic corrections [21]
 , (61)
, (61)
and with all the indices fixed, 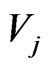 denotes mixing matrix elements in the two dimension
denotes mixing matrix elements in the two dimension 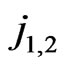 space,
space, 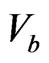 means the same but in the d-like squark sector. We obtain
means the same but in the d-like squark sector. We obtain  GeV if
GeV if  and
and 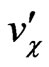 have the values already giving above.
have the values already giving above.
6.2. Neutralinos
Like in the case of the charged sector, the neutral lepton masses are given by the mixing among neutrinos, gauginos and higgsinos. The mass term in the basis
 , (62)
, (62)
is given by  where (63).
where (63).
 (63)
(63)
All parameters in Equation (63), but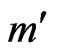 , are defined in Equations (20), (55) and (58);
, are defined in Equations (20), (55) and (58); ![]() and
and 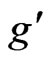 denote the gauge coupling constant of
denote the gauge coupling constant of  and
and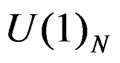 , respectively.
, respectively.
The neutralino mass matrix is diagonalized by a 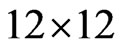 rotation unitary matrix
rotation unitary matrix , satisfying
, satisfying
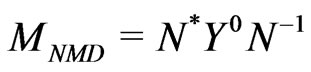 , (64)
, (64)
and the mass eigenstates are
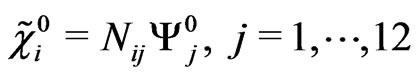 . (65)
. (65)
We can define the following Majorana spinor to represent the mass eigenstates
 . (66)
. (66)
As above the subindices  run over the lepton generations
run over the lepton generations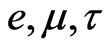 .
.
We get, considerating Equations (55)-(59) and 
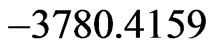 GeV, the following mass spectrum (in GeV), see mass matrix in Equation (63), to the neutralinos at the tree level
GeV, the following mass spectrum (in GeV), see mass matrix in Equation (63), to the neutralinos at the tree level
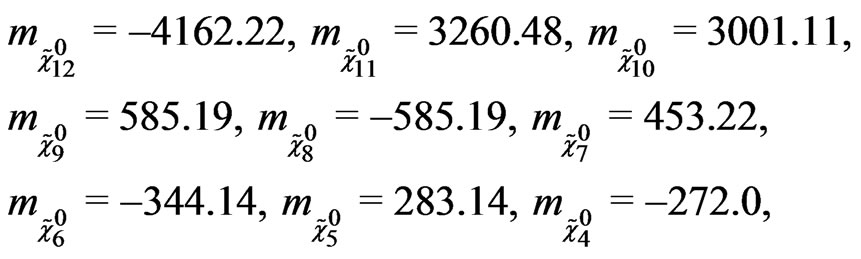 (67)
(67)
and for the three neutrinos we obtain (in eV)
![]() . (68)
. (68)
The neutrino masses in Equation (68) are of the order of magnitude for LSND and solar neutrino data.
6.3. Double Charged Charginos
We will use the following notation
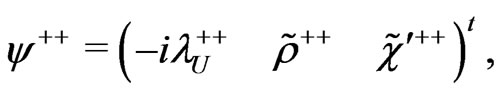
 and
and
 , (69)
, (69)
we can write the following equation [15]
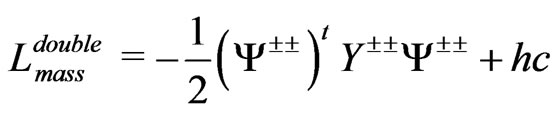 , (70)
, (70)
where
 , (71)
, (71)
with Equation (72).
 (72)
(72)
The matrix 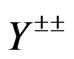 in Equation (71) satisfy the following relation
in Equation (71) satisfy the following relation
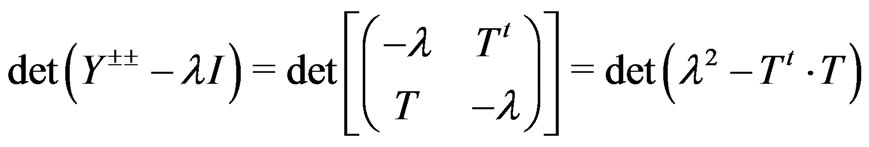 (73)
(73)
so we only have to calculate  to obtain the eigenvalues. Since
to obtain the eigenvalues. Since  is a symmetric matrix,
is a symmetric matrix, 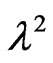 must be real, and positive because
must be real, and positive because  is also symmetric.
is also symmetric.
The double chargino mass matrix is diagonalized using two rotation matrices,  and
and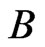 , defined by
, defined by
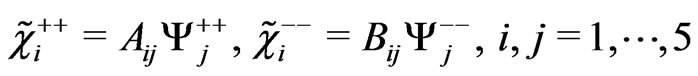 . (74)
. (74)
where  and
and 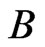 are unitary matrices such that
are unitary matrices such that
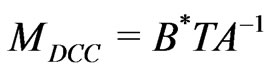 , (75)
, (75)
the matrix ![]() is defined in Equation (70). To determine
is defined in Equation (70). To determine 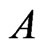 and
and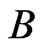 , we note that
, we note that
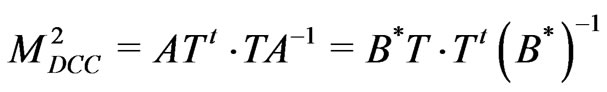 , (76)
, (76)
which means that 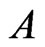 diagonalizes
diagonalizes 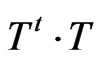 while
while  diagonalizes
diagonalizes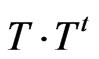 . It means
. It means
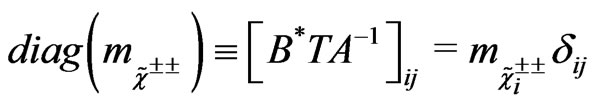 . (77)
. (77)
We performe the diagonalization procedure, as used to charginos and neutralinos. We get the following numerical results in 
![]()
![]() .
.
We can say from the values presented above and from Neutralinos that we can detect at ILC or LHC double charginos (since  until at least
until at least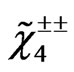 ) and neutralinos (since
) and neutralinos (since  until at least
until at least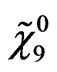 ) using the processes given at Equations (45,47) at ILC or LHC.
) using the processes given at Equations (45,47) at ILC or LHC.
We define the following Dirac spinors to represent the mass eigenstates:
 (78)
(78)
where  is the particle and
is the particle and  is the anti-particle, (we are using the same notation as in [20]).
is the anti-particle, (we are using the same notation as in [20]).
6.4. Quarks Masses
Let us first considered the u-quarks type. There are interactions like
 , (79)
, (79)
which imply a general mixing in the u-quark sector. Denoting
 , (80)
, (80)
where all the u-quarks fields are still Weyl spinors, we can also, define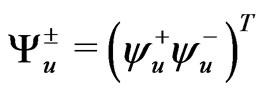 . We can define the mass term
. We can define the mass term  where
where 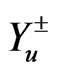 is given by:
is given by:
 , (81)
, (81)
with
 , (82)
, (82)
where the VEVs are defined in Equation (20).
The u-quarks mass matrix 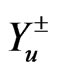 is diagonalized using two rotation matrices,
is diagonalized using two rotation matrices, 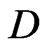 and
and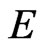 , defined by
, defined by
 . (83)
. (83)
Then we can write the diagonal matrix ( and
and 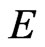 are unitary) as
are unitary) as
 . (84)
. (84)
In order to determine  and
and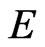 , we note that
, we note that
 , (85)
, (85)
and define the following Dirac spinors
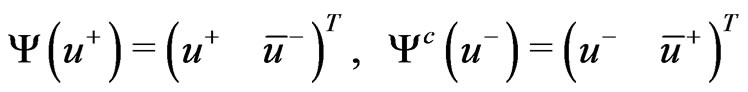 . (86)
. (86)
We can perform similar analyses to the d-quark sector. There are interactions like
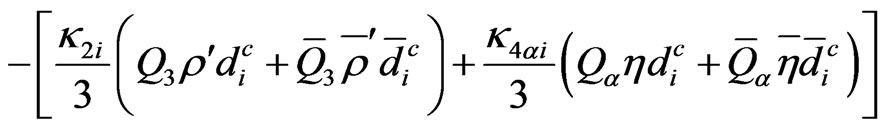 (87)
(87)
which imply a general mixing in the d-quark sector. Denoting
 , (88)
, (88)
where all the d-quarks fields are still Weyl spinors, we can also, define  We can define the mass term
We can define the mass term  where
where 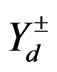 is given by:
is given by:
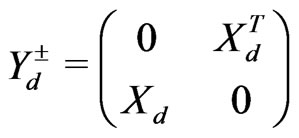 , (89)
, (89)
with
 , (90)
, (90)
where all the VEVs are defined in Equation (20).
The d-quarks mass matrix 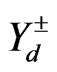 is diagonalized using two rotation matrices,
is diagonalized using two rotation matrices, 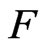 and
and , defined by
, defined by
 . (91)
. (91)
We can determine  and
and 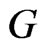 in the following way
in the following way
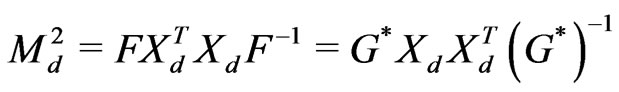 , (92)
, (92)
and define the following Dirac spinors
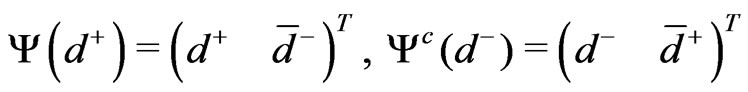 . (93)
. (93)
In general the Yukawa couplings  and
and 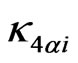 are different of zero and all quarks get their masses as happen in the SM and in the MSSM. However, we know that the quarks
are different of zero and all quarks get their masses as happen in the SM and in the MSSM. However, we know that the quarks 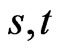 are heavier then the quark
are heavier then the quark  and the quark
and the quark ![]() is lighter than the quark
is lighter than the quark![]() .
.
We can try to given an reasonable explanation about these mass hierarchy in this model. In order to get this explanation we can suppose that the Yukawa couplings  are much smaller than the other Yukawa couplings that appear at mass matrices of the usual quarks. This hypothesis means we are going to neglect the mixing between the first and second familly with the first familly.
are much smaller than the other Yukawa couplings that appear at mass matrices of the usual quarks. This hypothesis means we are going to neglect the mixing between the first and second familly with the first familly.
Under this supposition we can rewrite our mass matrices, given at Equations (82), (90), in the following way
 ,
,
 (94)
(94)
We know from Equation (59) that 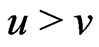 then Equation (94) explain why the quarks of charge
then Equation (94) explain why the quarks of charge  are heavier than the quarks of charge
are heavier than the quarks of charge .
.
By another way
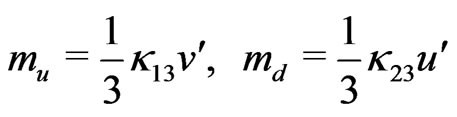 , (95)
, (95)
but, from Equation (59) we notice that  and if
and if 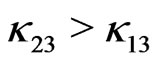 we can explain why
we can explain why ![]() -quark is a little more heavier than
-quark is a little more heavier than ![]() -quark.
-quark.
There are another way to try to explain the mass hierarchy between the fermions. If we look from Equations (50,82,90), it is easy to note that we can prevent u, d, s and e from picking up tree-level masses. To get this result we need to impose the following  symmetry on the Lagrangian
symmetry on the Lagrangian
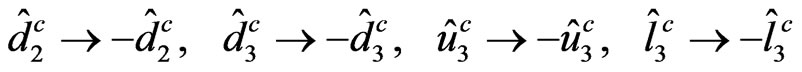 , (96)
, (96)
the others superfields are even under this symmetry as showed at Ref. [51]. On this case, it was showed that under 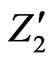 symmetry the heavy quarks
symmetry the heavy quarks 
 and
and  acquire mass at tree level while the light quarks (
acquire mass at tree level while the light quarks ( ) get their mass at 1-loop level.
) get their mass at 1-loop level.
There is another intersting possibility to get![]() ,
, ![]() light. We can introduce a new discrete
light. We can introduce a new discrete  flavor symmetry as done in [52].
flavor symmetry as done in [52].
6.5. Masses of Exotic Quarks
We will consider the J-quark type. There are interactions like
 , (97)
, (97)
which imply one diagonalized state with the following mass
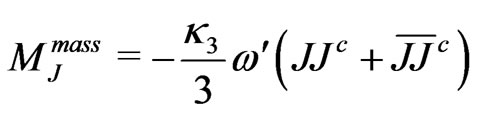 . (98)
. (98)
The another exotic quark j. There are interactions like
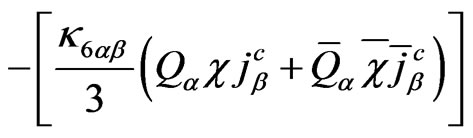 , (99)
, (99)
which imply a general mixing in the j-quark sector. Denoting
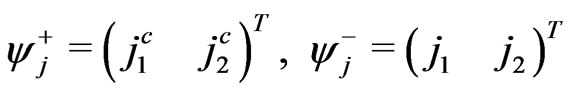 , (100)
, (100)
where all the j-quarks fields are still Weyl spinors, we can also, define 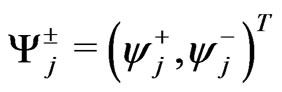 We can define the mass term
We can define the mass term 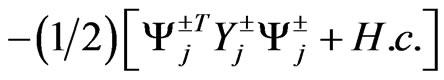 where
where 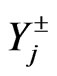 is given by:
is given by:
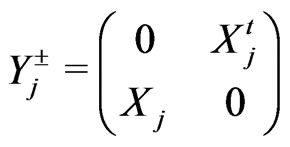 , (101)
, (101)
with
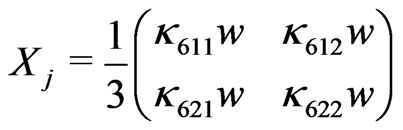 , (102)
, (102)
where the values VEVs are defined in Equation (20).
The j-quarks mass matrix is diagonalized using two rotation matrices, 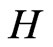 and
and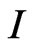 , defined by
, defined by
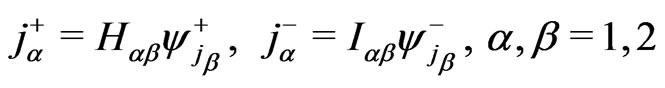 . (103)
. (103)
Then we can write the diagonal matrix ( and
and 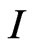 are unitary) as
are unitary) as
 . (104)
. (104)
We note that
 . (105)
. (105)
The masses of physical  are
are
 ,
,
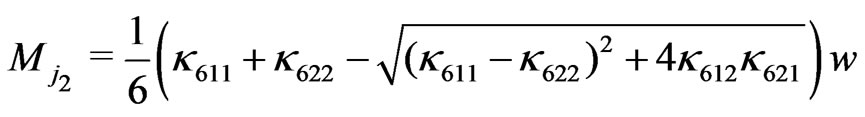 .(106)
.(106)
Notice that if 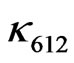 is zero we get that
is zero we get that
 , (107)
, (107)
therefore 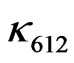 and
and 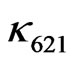 can be both zero that both
can be both zero that both  and
and  are massive.
are massive.
If we consider that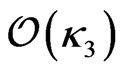 ,
, 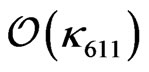 and
and  are the same order, for example
are the same order, for example  for example, it means from Equations (59), (98), (107) that
for example, it means from Equations (59), (98), (107) that ![]() -quark is heavier than
-quark is heavier than  quarks and their masses are in TeV scale.
quarks and their masses are in TeV scale.
We define the following Dirac spinors
 . (108)
. (108)
6.6. The Masses of Gluinos
It is well known gluinos are the supersymmetric partners of the gluons. Therefore gluinos, as in the MSSM, are the color octet fermions in the model and due the fact that the  group is unbroken, it means the gluinos can not mix with any others particles in the model, then they are already mass eigenstates.
group is unbroken, it means the gluinos can not mix with any others particles in the model, then they are already mass eigenstates.
Their mass, is one of the soft parameter that break SUSY, can be written as
 (109)
(109)
so that its mass at tree level is , as denoted at Equation (16) and Refs. [12-15], where
, as denoted at Equation (16) and Refs. [12-15], where
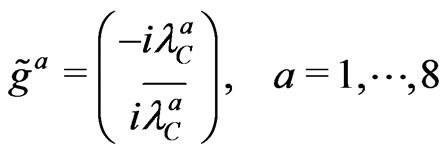 (110)
(110)
is the Majorana four-spinor defining the physical gluinos states.
6.7. Gauge Bosons Masses
The gauge mass term is given by 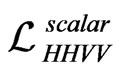 which we can divided in
which we can divided in  and
and , see Refs. [12-15].
, see Refs. [12-15].
The neutral gauge boson mass is given by
 , (111)
, (111)
where
 (112)
(112)
with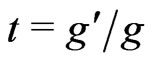 .
.
In the approximation that , the masses of the neutral gauge bosons are:
, the masses of the neutral gauge bosons are: ,
,  and
and , and the masses are given by
, and the masses are given by
 (113)
(113)
The charged gauge boson mass term,  see Refs. [12-15], can be written as
see Refs. [12-15], can be written as
 (114)
(114)
where
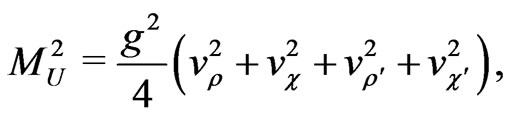
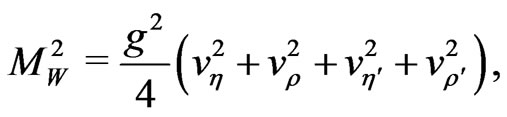
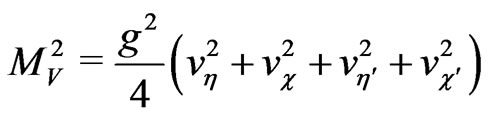 . (115)
. (115)
Comparing Equations (113), (115) we can conclude
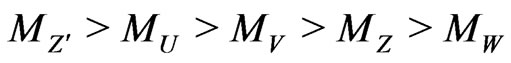 . (116)
. (116)
Using 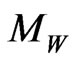 given in Equation (115) and
given in Equation (115) and  in Equation (113) we get the following relation:
in Equation (113) we get the following relation:
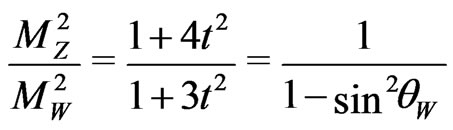 , (117)
, (117)
therefore we obtain
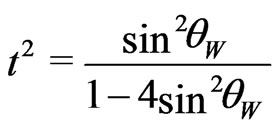 . (118)
. (118)
We want to mention that the gauge boson sector is exactly the same as in the non-supersymmetric 3-3-1 model.
We use Equation (59) in Equations (113,115) to get the following masses values for the gauge bosons
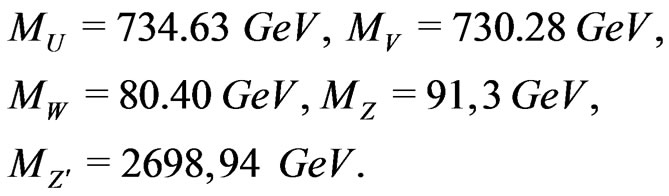 (119)
(119)
These values satisfy the Equation (116) and  and
and  are in agreement with the experimental limits. The lower limit in
are in agreement with the experimental limits. The lower limit in  boson is
boson is  GeV [53] and our mass is in agreement with this experimental limit.
GeV [53] and our mass is in agreement with this experimental limit.
7. Conclusions
In this paper we have presented new R-symmetry for the minimal supersymmetric  model and studied all the spectrum from the fermion's sector and gauged’s boson sector of this model. We also show that some of the new state as
model and studied all the spectrum from the fermion's sector and gauged’s boson sector of this model. We also show that some of the new state as ,
,  ,
,  ,
, 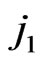 and
and ![]() can be discovered by LHC or same ILC, if they really exist.
can be discovered by LHC or same ILC, if they really exist.
The new R-parity not only provides a simple mechanism for the mass generation of the neutrinos but also gives some lepton flavor violating interactions at the tree level. This will play some important phenomenology in our model such as the proton’s stability, forbiddance of the neutron-antineutron oscillation and neutrinoless double beta decay.
8. Acknowledgments
This work was financed by the Brazilian funding agency CNPq, under contract number 309564/2006-9.
REFERENCES
- M. Singer, J. W. F. Valle and J. Schechter, “Canonical Neutral-Current Predictions from the Weak-Electromagnetic Gauge Group
 ,” Physical Review, Vol. D22, No. 3, 1980, pp. 738-743. doi:10.1103/PhysRevD.22.738
,” Physical Review, Vol. D22, No. 3, 1980, pp. 738-743. doi:10.1103/PhysRevD.22.738 - F. Pisano and V. Pleitez, “An
 Model for Electroweak Interactions,” Physical Review, Vol. D46, No. 1, 1992, pp. 410-417. doi:10.1103/PhysRevD.46.410
Model for Electroweak Interactions,” Physical Review, Vol. D46, No. 1, 1992, pp. 410-417. doi:10.1103/PhysRevD.46.410 - R. Foot, O. F. Hernandez, F. Pisano and V. Pleitez, “Lepton Masses in an
 Gauge Model,” Physical Review, Vol. D47, 1993, pp. 4158-4161. doi:10.1103/PhysRevD.47.4158
Gauge Model,” Physical Review, Vol. D47, 1993, pp. 4158-4161. doi:10.1103/PhysRevD.47.4158 - R. Foot, H. N. Long and T. A. Tran, “
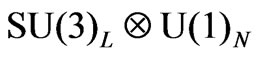 and
and  Gauge Models with Right-Handed Neutrinos,” Physical Review, Vol. D50, 1994, pp. 34-38. doi:10.1103/PhysRevD.50.R34
Gauge Models with Right-Handed Neutrinos,” Physical Review, Vol. D50, 1994, pp. 34-38. doi:10.1103/PhysRevD.50.R34 - J. C. Montero, F. Pisano and V. Pleitez, “Neutral Currents and GIM Mechanism in
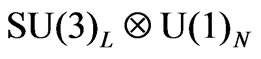 Model for Electroweak Interactions,” Physical Review, Vol. D47, 1993, pp. 2918-2929. doi:10.1103/PhysRevD.47.2918
Model for Electroweak Interactions,” Physical Review, Vol. D47, 1993, pp. 2918-2929. doi:10.1103/PhysRevD.47.2918 - H. N. Long, “
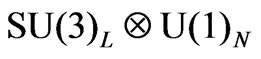 Model for Right-Handed Neutrino Neutral Currents,” Physical Review, Vol. D54, 1996, pp. 4691-4693. doi:10.1103/PhysRevD.54.4691
Model for Right-Handed Neutrino Neutral Currents,” Physical Review, Vol. D54, 1996, pp. 4691-4693. doi:10.1103/PhysRevD.54.4691 - H. N. Long, “
 Model with Right-Handed Neutrinos,” Physical Review, Vol. D53, No. 1, 1996, pp. 437-445. doi:10.1103/PhysRevD.53.437
Model with Right-Handed Neutrinos,” Physical Review, Vol. D53, No. 1, 1996, pp. 437-445. doi:10.1103/PhysRevD.53.437 - P. V. Dong and H. N. Long, “Electric Charge Quantization in
 Models,” International Journal of Modern Physics, Vol. A21, 2006, pp. 6677-6692. doi:10.1142/S0217751X06035191
Models,” International Journal of Modern Physics, Vol. A21, 2006, pp. 6677-6692. doi:10.1142/S0217751X06035191 - H. N. Long and V. T. Van, “Quark Family Discrimination and Flavor Changing Neutral Currents in the
 Model with Right-Handed Neutrinos,” Journal of Physics, Vol. G25, 1999, pp. 2319-2324.
Model with Right-Handed Neutrinos,” Journal of Physics, Vol. G25, 1999, pp. 2319-2324. - H. N. Long and N. Q. Lan, “Selfinteracting Dark Matter and Higgs Bosons in the
 Model with Right-Handed Neutrinos,” Europhysics Letters, Vol. 64, No. 4, 2003, pp. 571-577. doi:10.1209/epl/i2003-00267-5
Model with Right-Handed Neutrinos,” Europhysics Letters, Vol. 64, No. 4, 2003, pp. 571-577. doi:10.1209/epl/i2003-00267-5 - V. Pleitez and M. D. Tonasse, “Heavy Charged Leptons in an
 Model,” Physical Review, Vol. D48, No. 5, 1993, pp. 2353-2355. doi:10.1103/PhysRevD.48.2353
Model,” Physical Review, Vol. D48, No. 5, 1993, pp. 2353-2355. doi:10.1103/PhysRevD.48.2353 - T. V. Duong and E. Ma, “Supersymmetric
 Gauge Models: Higgs Structure at the Electroweak Energy Scale,” Physics Letters, Vol. B316, 1993, pp. 307- 311. doi:10.1016/0370-2693(93)90329-G
Gauge Models: Higgs Structure at the Electroweak Energy Scale,” Physics Letters, Vol. B316, 1993, pp. 307- 311. doi:10.1016/0370-2693(93)90329-G - H. N. Long and P. B. Pal, “Nucleon Instability in a Supersymetric
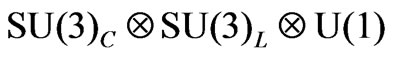 Model,” Modern Physical Letters, Vol. A13, 1998, pp. 2355-2360. doi:10.1142/S0217732398002503
Model,” Modern Physical Letters, Vol. A13, 1998, pp. 2355-2360. doi:10.1142/S0217732398002503 - J. C. Montero, V. Pleitez and M. C. Rodriguez, “A Supersymmetric 3-3-1 Model,” Physical Review, Vol. D65, 2002, Article ID 035006, pp. 1-13.
- M. Capdequi-Peyranère and M. C. Rodriguez, “Charginos and Neutralinos Production at 3-3-1 Supersymmetric Model in
 Scattering,” Physical Review, Vol. D65, 2002, Article ID 035001, pp. 1-16.
Scattering,” Physical Review, Vol. D65, 2002, Article ID 035001, pp. 1-16. - J. C. Montero, V. Pleitez and M. C. Rodriguez, “Supersymmetric 3-3-1 Model with Right-Handed Neutrinos,” Physical Review, Vol. D70, 2004, Article ID 075004, pp. 1-8. doi:10.1103/PhysRevD.70.075004
- D. T. Huong, M. C. Rodriguez and H. N. Long, “Scalar Sector of Supersymmetric
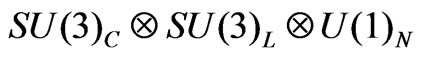 Model with Right-Handed Neutrinos,” arXiv: hep-ph/0508045.
Model with Right-Handed Neutrinos,” arXiv: hep-ph/0508045. - P. V. Dong, D. T. Huong, M. C. Rodriguez and H. N. Long, “Supersymmetric Economical 3-3-1 Model,” Nuclear Physics, Vol. B772, 2007, pp. 150-174. doi:10.1016/j.nuclphysb.2007.03.003
- M. C. Rodriguez, “Scalar Sector in the Minimal SuperSymmetric 3-3-1 Model,” International Journal of Modern Physics, Vol. A 21, 2006, pp. 4303-4322. doi:10.1142/S0217751X06031600
- H. E. Haber and G. L. Kane, “The Search for Supersymmetry: Probing Physics beyond the Standard Model,” Physics Reports, Vol. 117, No. 2-4, 1985, pp. 75-263. doi:10.1016/0370-1573(85)90051-1
- J. C. Montero, V. Pleitez and M. C. Rodriguez, “Lepton Masses in a Supersymmetric 3-3-1 Model,” Physical Review, Vol. D 65, 2002, Article ID 095008, pp. 1-11.
- P. Fayet, “Supergauge Invariant Extension of the Higgs Mechanism and a Model for the Electron and Its Neutrino,” Nuclear Physics, Vol. B90, pp. 1975, pp. 104-124. doi:10.1016/0550-3213(75)90636-7
- P. Fayet, “Supersymmetry and Weak, Electromagnetic and Strong Interactions,” Physics Letters, Vol. B64, 1976, pp. 159-162. doi:10.1016/0370-2693(76)90319-1
- P. Fayet, “Spontaneously Broken Supersymmetric Theories of Weak, Electromagnetic and Strong Interactions,” Physics Letters, Vol. B69, 1977, pp. 489-494. doi:10.1016/0370-2693(77)90852-8
- P. Fayet, “Mixing Between Gravitational and Weak Interactions through the Massive Gravitino,” Physics Letters, Vol. B70, 1977, pp. 461-464. doi:10.1016/0370-2693(77)90414-2
- P. Fayet, In: A. Perlmutter and L. F. Scott, Eds., New Frontiers in High-Energy Physics, Proceedings of Orbis Scientiae, Coral Gables, Plenum, New York, 1978, p. 413.
- M. C. Rodriguez, “History of Supersymmetric Extensions of the Standard Model,” International Journal of Modern Physics, Vol. A25, 2010, pp. 1091-1121. doi:10.1142/S0217751X10048950
- S. Dawson, E. Eichten and C. Quigg, “Search for Supersymmetric Particles in Hadron-Hadron Collisions,” Physical Review, Vol. D31, 1985, pp. 1581-1637. doi:10.1103/PhysRevD.31.1581
- M. Dress, R. M. Godbole and P. Royr, “Theory and Phenomenology of Sparticles,” 1st Edition, World Scientific Publishing Co. Pte. Ltd., Singapore, 2004.
- H. Baer and X. Tata, “Weak Scale Supersymmetry: From Superfields to Scattering Events,” 1st Edition, Cambridge, 2006.
- J. Wess and J. Bagger, “Supersymmetry and Supergravity,” 2nd Edition, Princeton University Press, Princeton, 1992.
- L. Girardello and M. T. Grisaru, “Soft Breaking of Supersymmetry,” Nuclear Physics, Vol. B194, 1982, pp. 65- 76. doi:10.1016/0550-3213(82)90512-0
- J. C. Montero, V. Pleitez and M. C. Rodriguez, “Leftright Asymmetries in Polarized Lepton Lepton Scattering,” Physical Review, Vol. D58, 1998, Article ID 094026, pp. 1-15.
- J. C. Montero, V. Pleitez and M. C. Rodriguez, “L-R Asymmetries and Signals for New Bosons,” AIP Conference Proceedings, Vol. 490, 1999, pp. 397-400.
- J. C. Montero, V. Pleitez and M. C. Rodriguez, “Leftright Asymmetries and Exotic Vector-Boson Discovery in Lepton Lepton Colliders,” International Journal of Modern Physics, Vol. A16, 2001, pp. 1147-1160. doi:10.1142/S0217751X01003275
- J. C. Montero, V. Pleitez and M. C. Rodriguez, “LeftRight Asymmetries in Polarized e Mu Scattering,” Physical Review, Vol. D58, 1998, Article ID 097505, pp. 1-4.
- E. Ramirez Barreto, Y. D. A. Coutinho and J. S. Borges, “Extra Neutral Gauge Boson from Two Versions of the 3-3-1 Model in Future Linear Colliders,” European Physical Journal, Vol. C50, 2007, pp. 909-917. doi:10.1140/epjc/s10052-007-0254-2
- E. R. Barreto, Y. D. A. Coutinho and J. S. Borges, “Bounds for Z' mass in 3-3-1 Models from
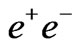 Collisions at ILC and CLIC Energies,” arXiv:hep-ph/0605098.
Collisions at ILC and CLIC Energies,” arXiv:hep-ph/0605098. - E. Ramirez Barreto, Y. D. A. Coutinho and J. S. Borges, “Four Leptons Production in
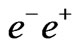 Collisions from 3-3-1 Model,” Physics Letters, Vol. B632, 2006, pp. 675- 679. doi:10.1016/j.physletb.2005.11.016
Collisions from 3-3-1 Model,” Physics Letters, Vol. B632, 2006, pp. 675- 679. doi:10.1016/j.physletb.2005.11.016 - Y. D. A. Coutinho, P. P. Queiroz Filho and M. D.
- Tonasse, “3-3-1 Exotic Quark Search at CERN LEPII-LHC,” Physical Review, Vol. D60, 1999, Article ID 115001, pp. 1-5. doi:10.1103/PhysRevD.60.115001
- A. Pukhov, E. Boos, M. Dubinin, V. Edneral, V. Ilyin, D. Kovalenko, A. Kryukov, V. Savrin, S. Shichanin and A. Semenov, “Comphep—A Package for Evaluation of Feynman Diagrams and Integration over Multi-Particle Phase Space,” arXiv:hep-ph/9908288.
- L. N. Hoang and D. V. Soa, “Trilinear Gauge Boson Couplings and Bilepton Production in the
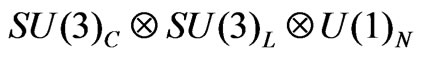 Models,” Nuclear Physics, Vol. B601, 2001, pp. 361-379. doi:10.1016/S0550-3213(01)00088-8
Models,” Nuclear Physics, Vol. B601, 2001, pp. 361-379. doi:10.1016/S0550-3213(01)00088-8 - D. T. Binh, D. T. Huong, T. T. Huong, L. N. Hoang and D. V. Soa, “Quartic Gauge Boson Couplings and Tree Unitarity in the
 Models,” Journal of Physics, Vol. G29, 2003, pp. 1213-1226. doi:10.1088/0954-3899/29/6/319
Models,” Journal of Physics, Vol. G29, 2003, pp. 1213-1226. doi:10.1088/0954-3899/29/6/319 - A. Salam and J. Strathdee, “Supersymmetry and Fermion Number Conservation,” Nuclear Physics, Vol. B87, 1975, pp. 85-92. doi:10.1016/0550-3213(75)90253-9
- R. Barbier, et al., “R-Parity Violating Supersymmetry,” Physical Report, Vol. 420, No. 1-6, 2005, pp. 1-202. doi:10.1016/j.physrep.2005.08.006
- G. Moreau, “Phenomenological Study of R Parity Symmetry Violating Interactions in Supersymmetric Theories," (In French), arXiv:hep-ph/0012156.
- H. Dreiner, “Am Introduction to Explict R-Parity Violation,” arXiv:hep-ph/9707435.
- P. V. Dong, D. T. Huong, M. C. Rodriguez and H. N. Long, “Neutrino Masses in Supersymmetric Economical
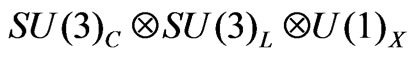 Model,” Journal of Modern Physics, Vol. 2, No. 8, 2011, pp. 792-802. doi:10.4236/jmp.2011.28093
Model,” Journal of Modern Physics, Vol. 2, No. 8, 2011, pp. 792-802. doi:10.4236/jmp.2011.28093 - M. C. Rodriguez, “Double Chargino Production in
 Scattering,” International Journal of Modern Physics, Vol. A22, 2008, pp. 6080-6088. doi:10.1142/S0217751X07039250
Scattering,” International Journal of Modern Physics, Vol. A22, 2008, pp. 6080-6088. doi:10.1142/S0217751X07039250 - M. C. Rodriguez, “A Supersymmetric 3-4-1 Model,” International Journal of Modern Physics, Vol. A22, 2007, pp. 6147-6167. doi:10.1142/S0217751X07037275
- C. M. Maekawa and M. C. Rodriguez, “Masses of Fermions in Supersymmetric Models,” Journal of High Energy Physics (JHEP), Vol. 4, 2006, p. 0604:031.
- S. Sen, “Quark Masses in Supersymmetric SU(3)(color) x SU(3)(W) x U(1)(X) Model with Discrete T-Prime Flavor Symmetry, Physical Review, Vol. D76, 2007, Article ID 115020, pp. 1-6. doi:10.1103/PhysRevD.76.115020
- W. M. Yao, et al., “Review of Particle Physics,” Journal of Physics, Vol. G33, 2006, pp. 1-1232.
Lagrangian
The goal of this Appendix is to present all terms in the lagrangian of the model, which we have used in this work.
A.1. Lepton Lagrangian
In the  term can be written as [31]
term can be written as [31]
 (120)
(120)
where
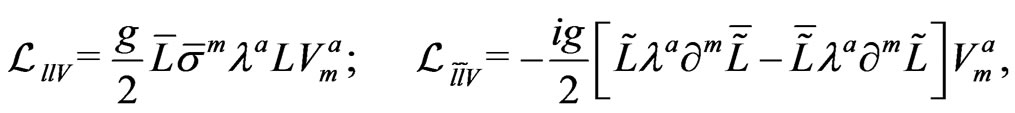
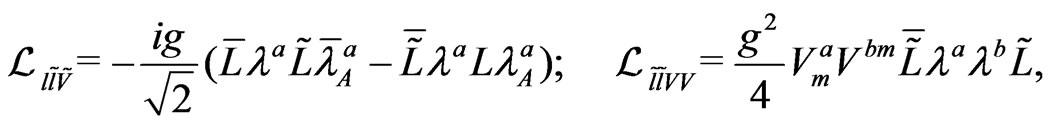
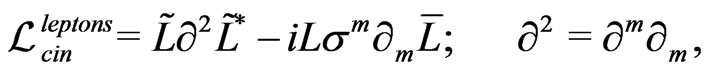
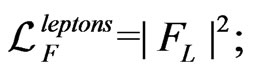
 (121)
(121)
A.2. Quark Lagrangian
As above we can write to the quarks
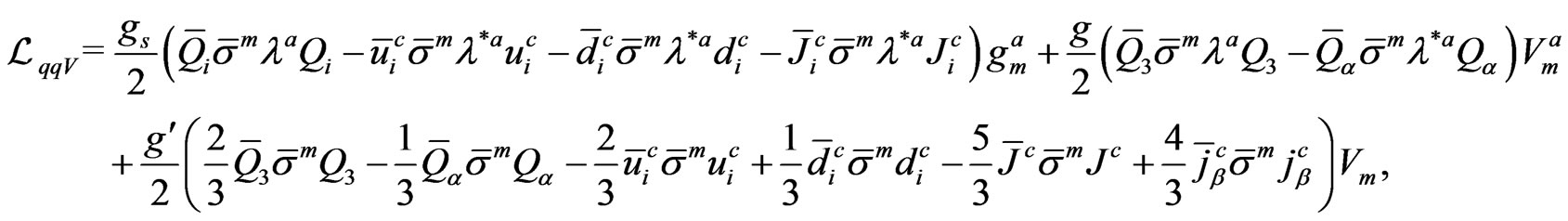
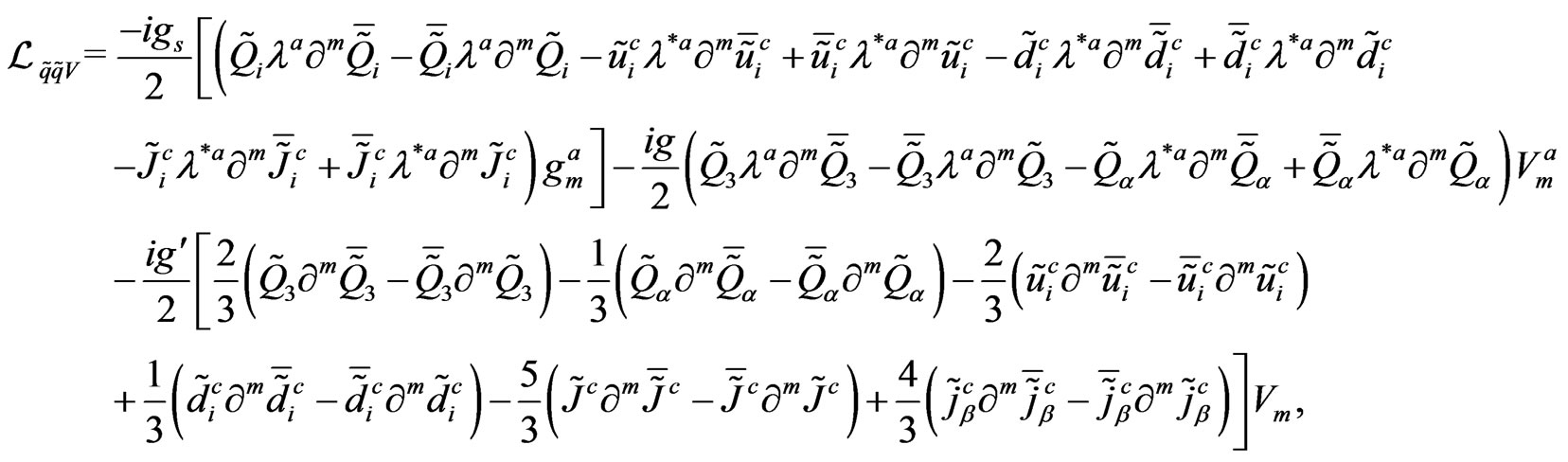


 ,
,
![]() ,
,

 (122)
(122)
A.3. Scalar Lagrangian
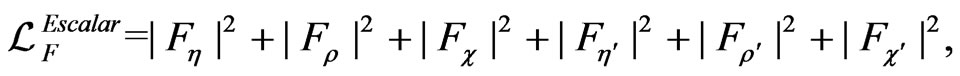
 ,
,
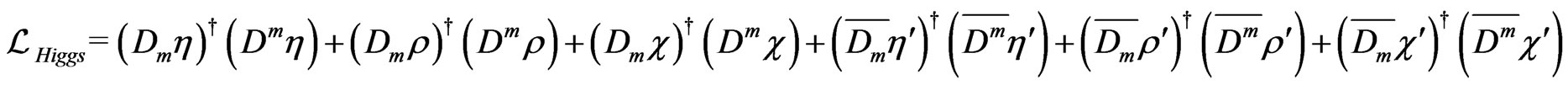 ,
,
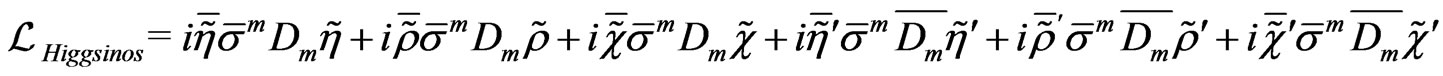 ,
,
 (123)
(123)
where the covariant derivative of  are given by:
are given by:

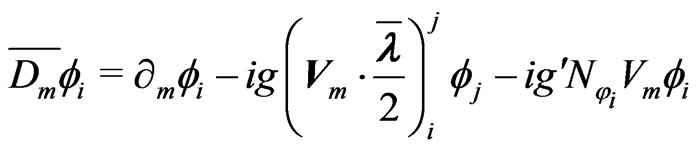 . (124)
. (124)
A.4. Gauge Lagrangian
Now we are dealing with  that can be expanded as
that can be expanded as
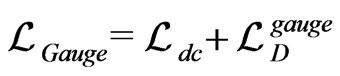 (125)
(125)
where
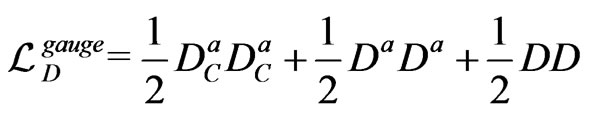 ,
,
 (126)
(126)
with
 ,
, 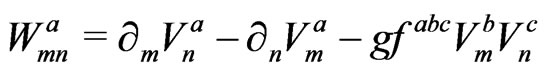 ,
,
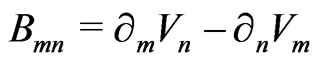 ,
, 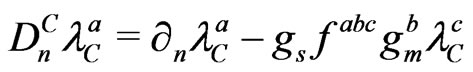 ,
, 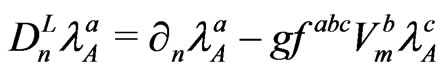 (127)
(127)
![]() are the constant structure of
are the constant structure of  gauge group.
gauge group.
A.5. Superpotential Lagrangian
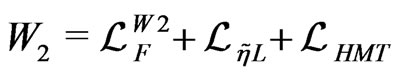 ,
,
 .(128)
.(128)
As componentes de cada lagrangiana são escritas como
 ,
,
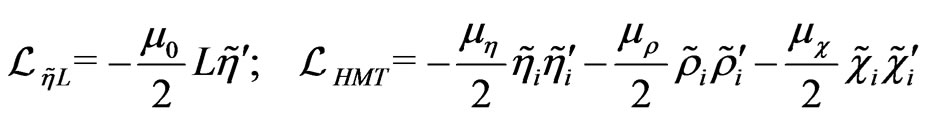 ,
,
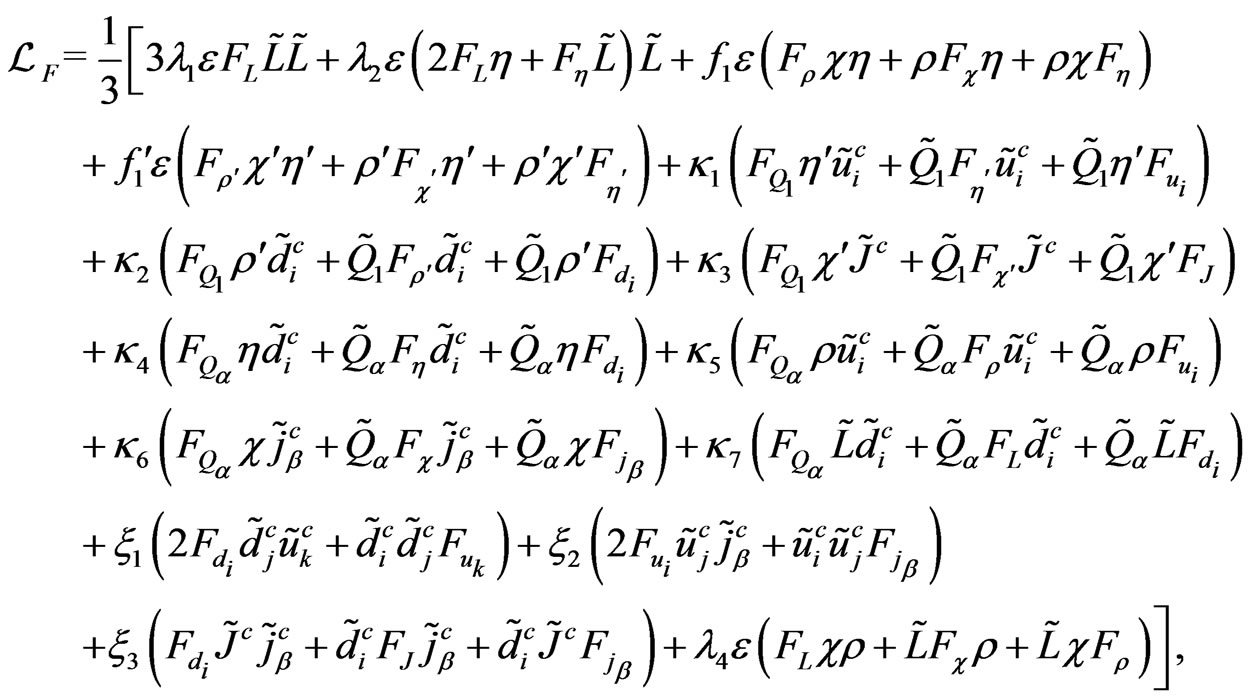
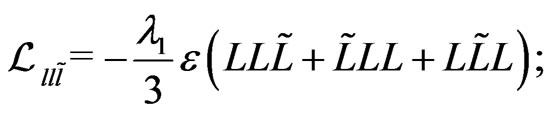
 ,
,
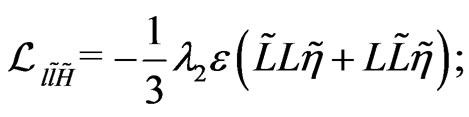

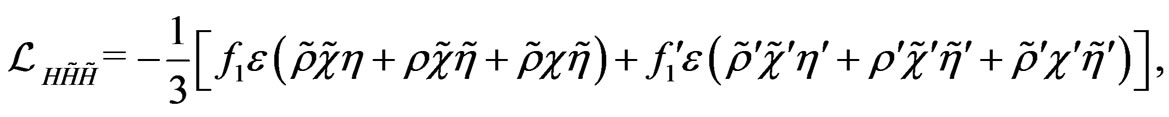
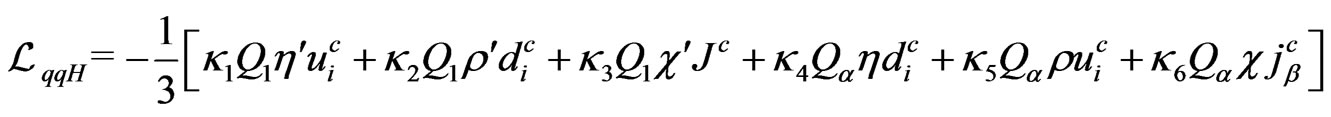 ,
,
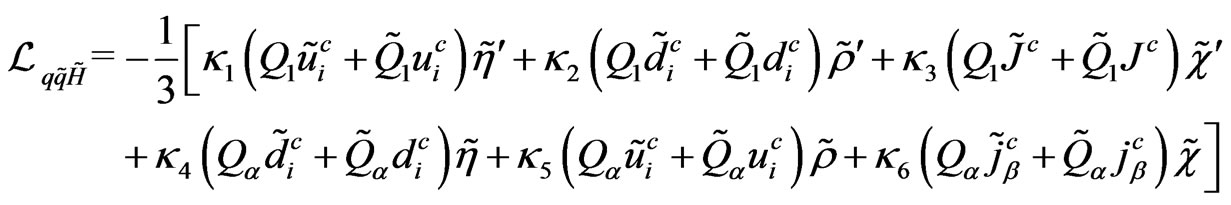
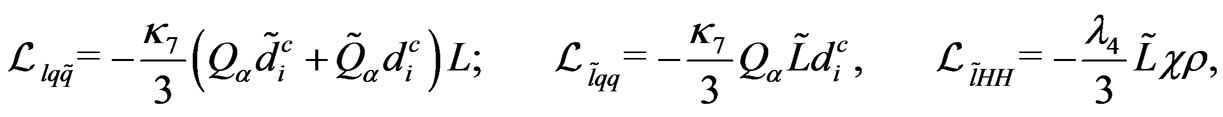
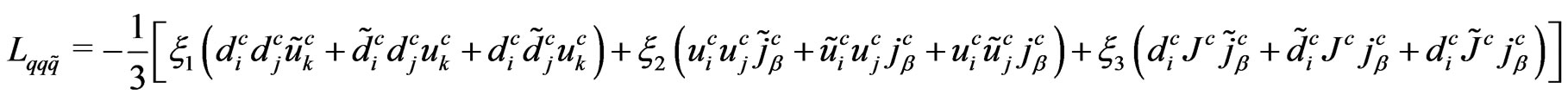 .(129)
.(129)
NOTES
1I would like to thanks E. Gregores that call my attention to this dangeours Higgs decay channel.
2I would like to thank to Alexander Belyaev that call my attention to the first process.

