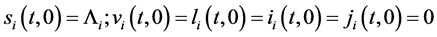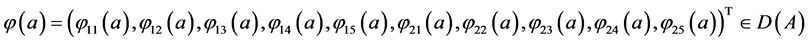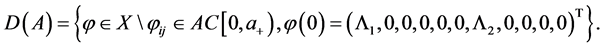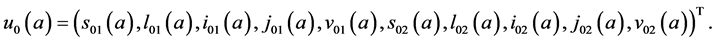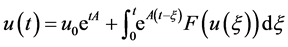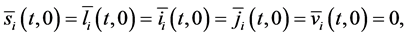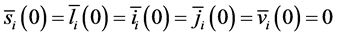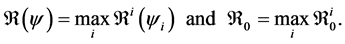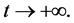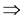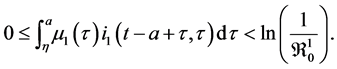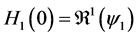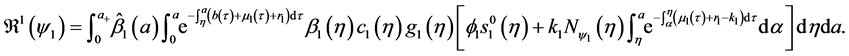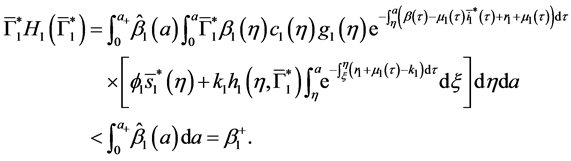Applied Mathematics
Vol.07 No.15(2016), Article ID:71090,21 pages
10.4236/am.2016.715155
Mathematical Analysis and Simulation of an Age-Structured Model of Two-Patch for Tuberculosis (TB)
Badjo Kimba Abdoul Wahid, Saley Bisso
Department of Mathematics and Computer Science, Abdou Moumouni University, Niamey, Niger

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 8, 2016; Accepted: September 27, 2016; Published: September 30, 2016
ABSTRACT
This paper studied a structured model by age of tuberculosis. A population divided into two parts was considered for the study. Each subpopulation is submitted to a program of vaccination. It was allowed the migration of vaccinated people only between the two patches. After the determination of 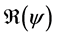 and
and , the local and global stability of the disease-free equilibrium was studied. It showed the existence of three endemic equilibrium points. The theoretical results were illustrated by a numeric simulation.
, the local and global stability of the disease-free equilibrium was studied. It showed the existence of three endemic equilibrium points. The theoretical results were illustrated by a numeric simulation.
Keywords:
Age-Structured, Reproductive Number, Two-Patch, TB, Stability, Simulation

1. Introduction
Tuberculosis (TB) (short for tubercle bacillus) is a widespread, infectious disease caused by various strains of mycobacteria, usually Mycobacterium tuberculosis (MTB). Tuberculosis typically attacks the lungs, but can also affect other parts of the body [1] . To be infected bacilli must penetrate deep into the alveoli, but the contagiousness of the disease is relatively low and depends on the immune system of subjects. Individuals at highest risk are young children, adults, deficient elderly, and people living in precarious socio-economic conditions, in nursing or whose immunity is deficient (AIDS, immunosuppressive therapy ...) [2] . This is one of the most common old infectious diseases [3] [4] , with about two billion people being currently infected. There are about nine million new cases of infection each year and two million deaths per year according to WHO estimations [3] [5] . For more information, many authors have worked on the epidemiology of tuberculosis [1] - [3] [5] - [13] . In many developing countries in general and sub-Saharan Africa particularly, TB is the leading cause of death, accounting for about two million deaths and a quarter of avoidable adult deaths [11] .
It is well known that factors such as the emergence of drug resistance against tuberculosis, the growth of the incidence of HIV in recent years, as well as other diseases favor the development of Koch bacillus in the body call for improved strategies to control this deadly disease [2] [10] [14] . Last May, the World Health Assembly approved an ambitious strategy for 20 years (2016-2035) to put an end to World TB epidemic (World Day of fight against tuberculosis―March 24, 2015). In literature, several articles discussed about coinfection: TB-HIV/AIDS and the most recent is [2] . Nowadays, it is not a secret for everyone that fighting against infectious diseases is also a fight against poverty. Humans are traditionally organized into well-defined social units, such as families, tribes, villages, cities, countries or regions are good examples of patches [11] [12] . For this study, two subpopulations were considered and each was subjected to a vaccination program. However, only the vaccinated individuals can migrate from one patch to another. Despite that we have neglected the relapse rate, to avoid any risk of treated individuals’ reactivation, any migration between patches was allowed. After proving that the problem is well defined and it has a unique solution if the initial condition is given, we are able to calculate the reproduction of numbers 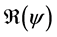 and
and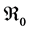 . We have established the existence conditions for three endemic equilibrium points, and the conditions of local and global stability of the equilibrium point without disease. Finally, numerical simulations illustrate clinical outcomes. This paper is organized as follows: Section 2 introduces the two-patch model structured in age to study the dynamics of TB transmission. The existence of positive and unique solutions is demonstrated in Section 3. The point of equilibrium without disease, reproductive numbers
. We have established the existence conditions for three endemic equilibrium points, and the conditions of local and global stability of the equilibrium point without disease. Finally, numerical simulations illustrate clinical outcomes. This paper is organized as follows: Section 2 introduces the two-patch model structured in age to study the dynamics of TB transmission. The existence of positive and unique solutions is demonstrated in Section 3. The point of equilibrium without disease, reproductive numbers 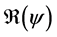 and
and  are defined in the section 4 with the local and global stability of the disease-free equilibrium point. The existence of three endemic equilibrium points is proven in Section 5. Some numerical simulation results are given in Section 6. In Section 7, we have a discussion, conclusion and further work.
are defined in the section 4 with the local and global stability of the disease-free equilibrium point. The existence of three endemic equilibrium points is proven in Section 5. Some numerical simulation results are given in Section 6. In Section 7, we have a discussion, conclusion and further work.
2. Parameters and Mathematical Model Formulation
Two-patch age structured model of tuberculosis was considered. The model is to split the population into two subpopulations. The recruitment is only possible in the class of susceptible and the vaccinated individuals were able to migrate between the two subpopulations. Each subpopulation is divided into five classes based on their epidemiological status: susceptible, vaccinated, latent, infectious or treated. We denote these subgroups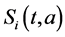 ,
, 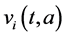 ,
, 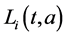 ,
, 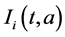 and
and 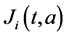 respectively. The birth rate of the patch i is
respectively. The birth rate of the patch i is ;
; 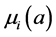 and
and 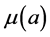 denote the mortality rate related to the disease relative to the patch i and the rate of natural mortality. The time and age depended of the force of infection of the subpopulation i is
denote the mortality rate related to the disease relative to the patch i and the rate of natural mortality. The time and age depended of the force of infection of the subpopulation i is  and vaccination rate is
and vaccination rate is ;
; 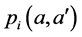 is the probability that an infective individual of age
is the probability that an infective individual of age 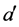 will have contact with and successfully infect a susceptible individual of age a,
will have contact with and successfully infect a susceptible individual of age a, 






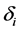

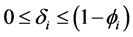
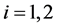
The age-structured model for the transmission of TB (see Figure 1) is described by the following system of partial differential equations:

with initial and boundary conditions:
and
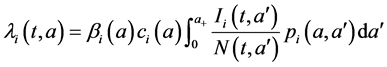
assume that assume that

Figure 1. Flow chart of the two-patch model for tuberculosis disease transmission.
(see Greenhalgh, 1988 [15] and Dietz Schenzle, 1985 [16] ), and
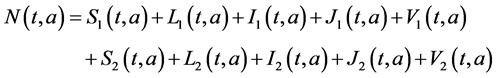
By summing equations of system (1) and (2), we obtain the following equations for the total population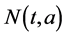

where
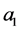
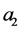
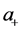

Let

The system (1) can be normalized as the following system:

with boundary conditions
with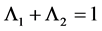
3. Existence of Positive Solutions
In this section we will prove that the system (5) has a unique positive solution, and to achieve this we will write the system (5) in compact form (abstract Cauchy problem).
Consider the Banach space X defined by 

where 



The state space of system (5), where
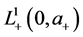

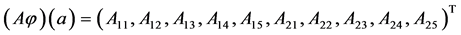
To determine the components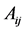
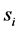
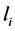



After replacing


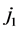
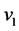
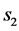
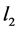

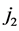


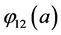
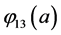

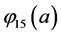
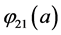


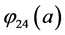
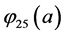

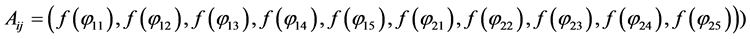
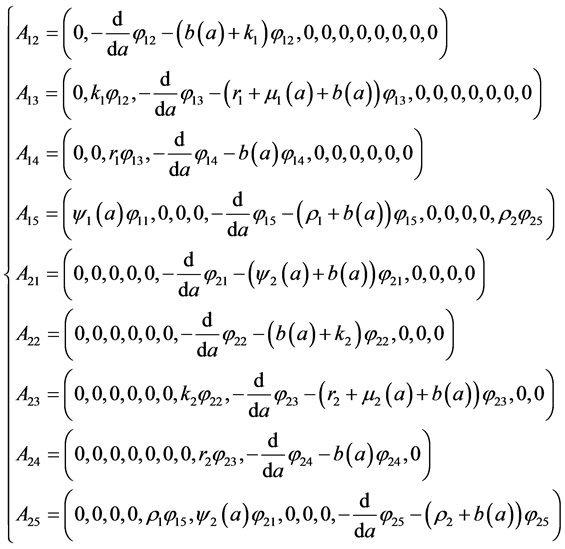
With
where 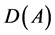
And 


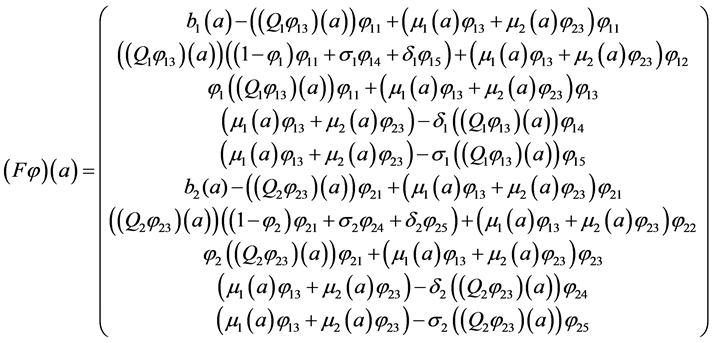
where 


Let
thus, we can rewrite the system (5) as an abstract Cauchy problem:
where
According to these results we have the following results (see [17] - [19] ):
Lemma 1. The operator F is continuously Fréchet differentiable on X.
Lemma 2. The operator A generates a 


Theorem 1. For each 
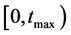


Proof. The proof of this theorem can be found in [18] - [20] . W
4. The Disease-Free Steady State
4.1. Determination of the Disease-Free Equilibrium
A steady state 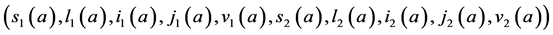

with initial value conditions
Therefore, we obtain the disease-free steady state
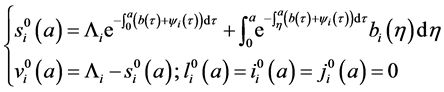
4.2. Calculation of the Reproduction Numbers 
To study the stability of the disease-free steady state, we denote the perturbations of system by
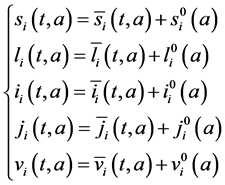
The perturbations satisfy the following equations:

with boundary conditions:
we consider the exponential solutions of system (16) of the form:
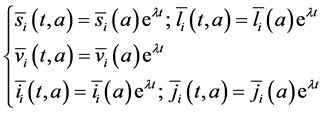
The system (16) becomes:
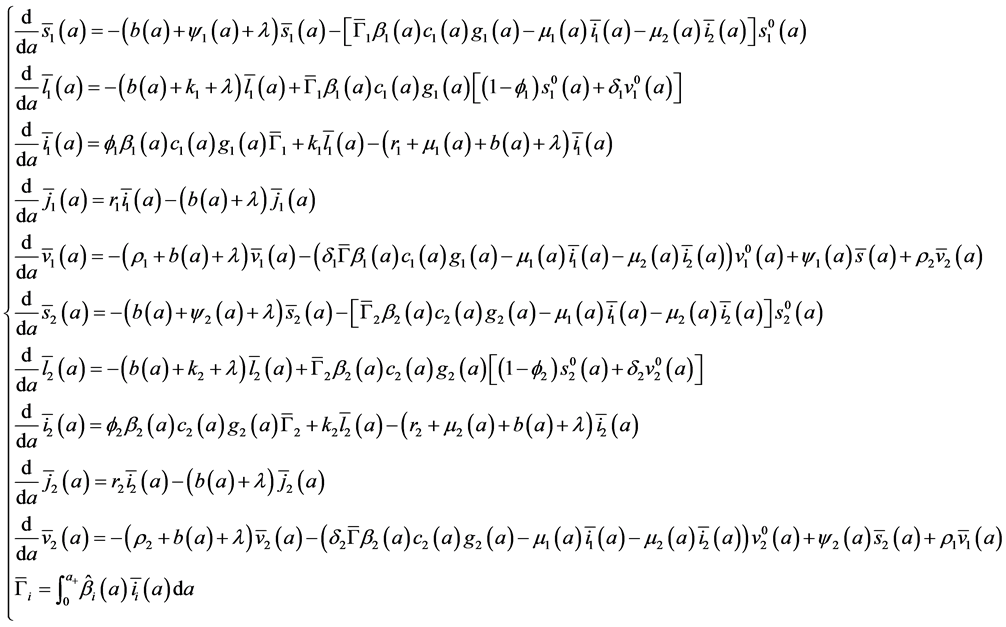
with boundary conditions:
Let
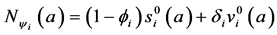
From Equation (18), we obtain:
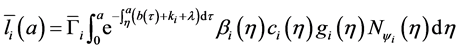
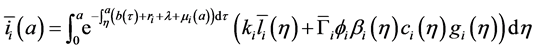
Hence, by Equations ((20) and (21)) after changing order of integration, we obtain:
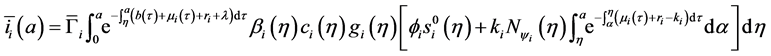
Injecting (22) in the expression of



Denote the right-hand side of Equation (23) by 
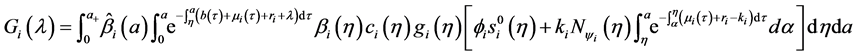
We define the net reproductive number as

We can obtain an expression for 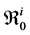
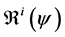
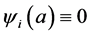
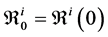
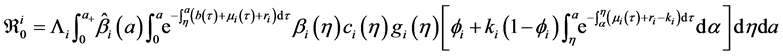
Let
4.3. Local Stability of the Disease-Free Equilibrium
Theorem 2. The infection-free steady-state (5) is locally asymptotically stable (l.a.s.) if 
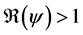
Proof. Noticing that
We know that Equation (23) has a unique negative real solution 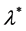
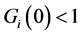
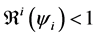



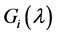

indicating that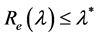
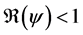
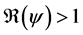
In this corollary, we have the three cases of the unstability of the disease free equilibrium.
Corollary 1. 1) whenever 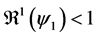
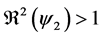
2) whenever 

3) whenever 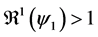
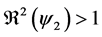
4.4. Global Stability of the Disease-Free Equilibrium
Since 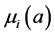
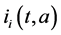
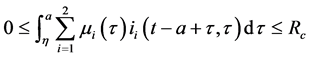
Corollary 2. Assume that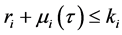
Theorem 3. The disease-free equilibrium of system (5) is globally asymptotically stable if 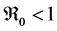

Proof. The proof consist to show that
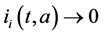

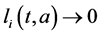
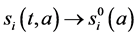
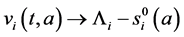
Integrating system (5) along characteristic lines we get
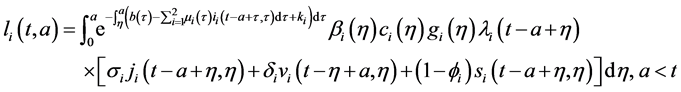
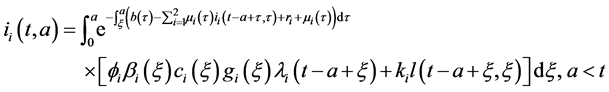
Injecting (27) in (28), and changing order of integration, we obtain:
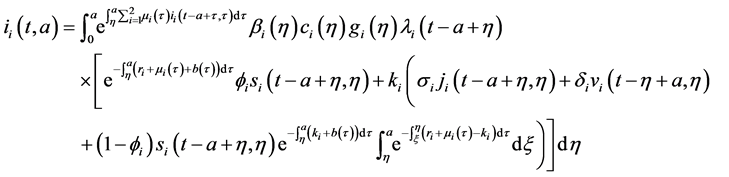
Injecting (29) in

By using corollary 2, inequality (*) and Fatou’s lemma, we have
Since
Corollary 3. The disease-free equilibrium is globally asymptotically in:
1) the first sub-population if 
2) the second sub-population if 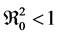
For this disease can disappear without any form of intervention, according to these results we must ensure that there is no new infected and the infectious rate does not reach a certain spread.
5. Existence of an Endemic State
There exists three endemic steady state of system (5) whenever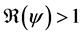
5.1. The First Boundary Endemic Equilibrium
Theorem 4. A boundary endemic equilibrium of the form 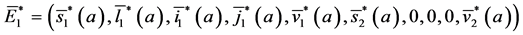
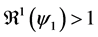
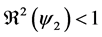
Proof. The method commonly used to find an endemic steady state for age-structure models consists of obtaining explicit expressions for a time independent solution of system (5)

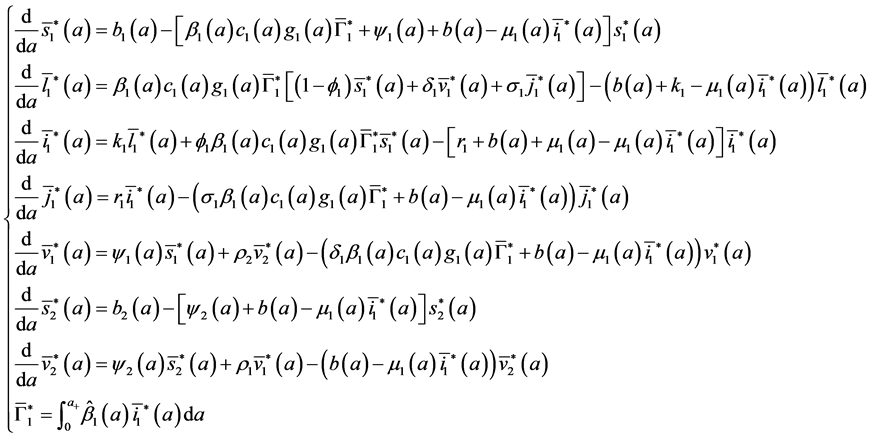
with the initial conditions:
Let
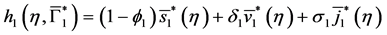
Integrating system (31), we obtain:


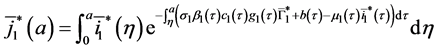
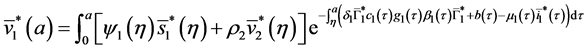


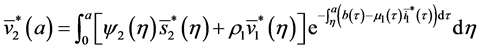
By injecting (37) in (34), we obtain:
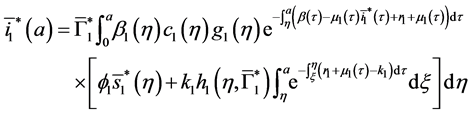
Injecting (40) in the expression of


Let
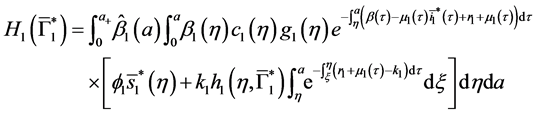
Since 
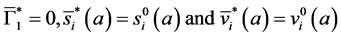
i.e.
We now see that an endemic steady state exists if Equation (41) has a positive solution.
Since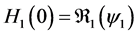
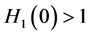
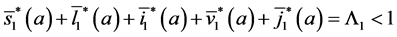
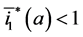
Since
In particular, for

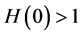

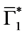

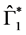

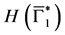
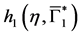
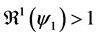
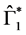
5.2. The Second Boundary Endemic Equilibrium
Theorem 5. A boundary endemic equilibrium of the form 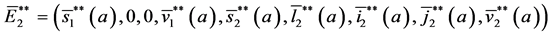

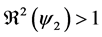
Proof. (Ideas of proof) 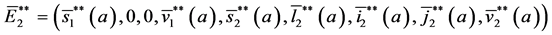
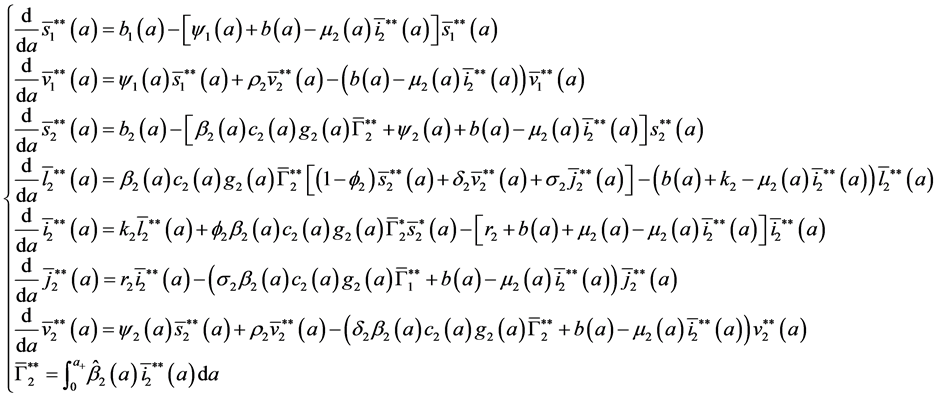
with the initial conditions:

Let

Integrating system (51), we obtain:

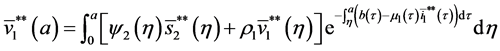

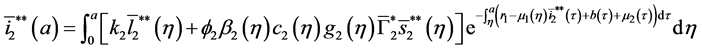

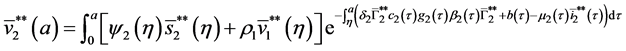
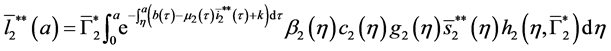
Hence, by the similar method using in theorem 4, we obtain the result. W
5.3. The Interior Endemic Equilibrium
Theorem 6. An interior endemic equilibrium of the form
whenever 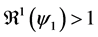

Proof. 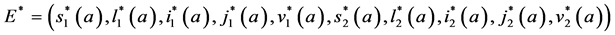
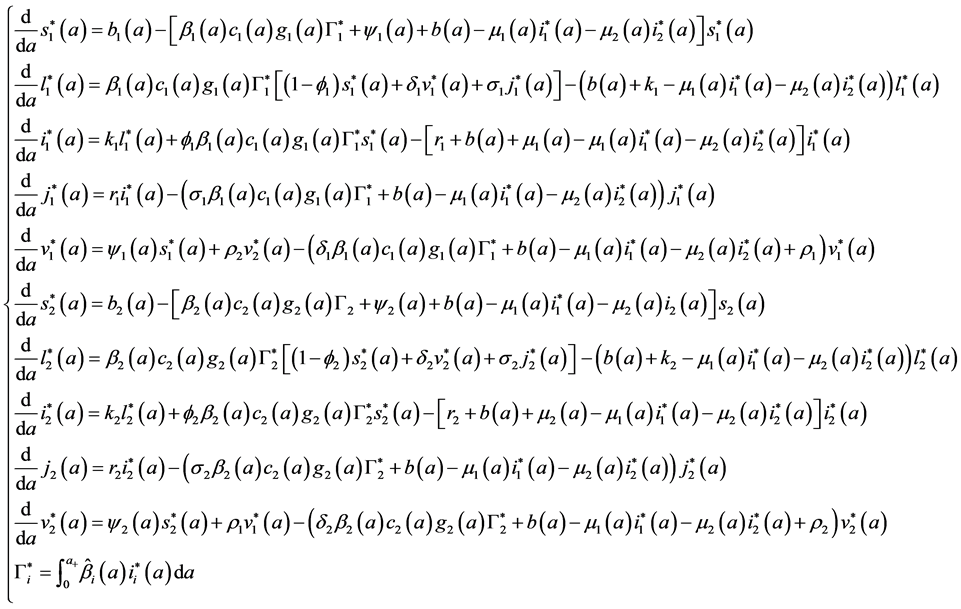
with the initial conditions:
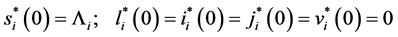
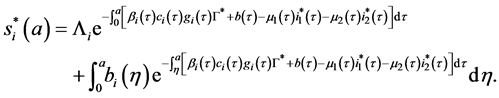
Let





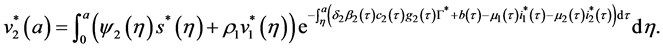
By injecting (58) in (59), we obtain:

By injecting (63) in the expression of
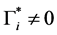
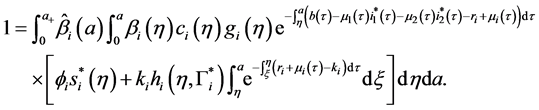
Let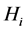

Since 


We now see that an endemic steady state exists if Equation (64) has a positive solution. Since
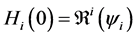

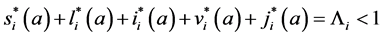
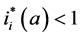
Since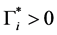
In particular, for
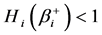
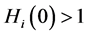

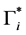
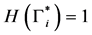


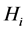


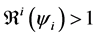

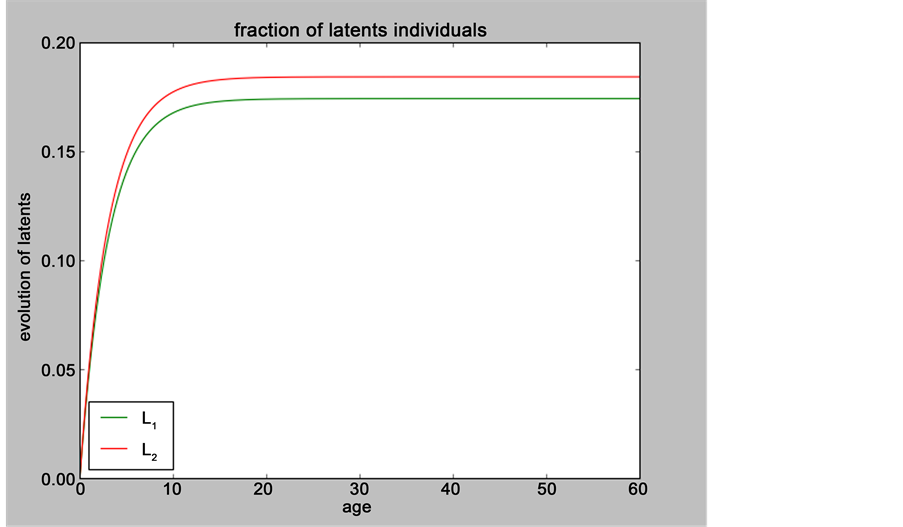
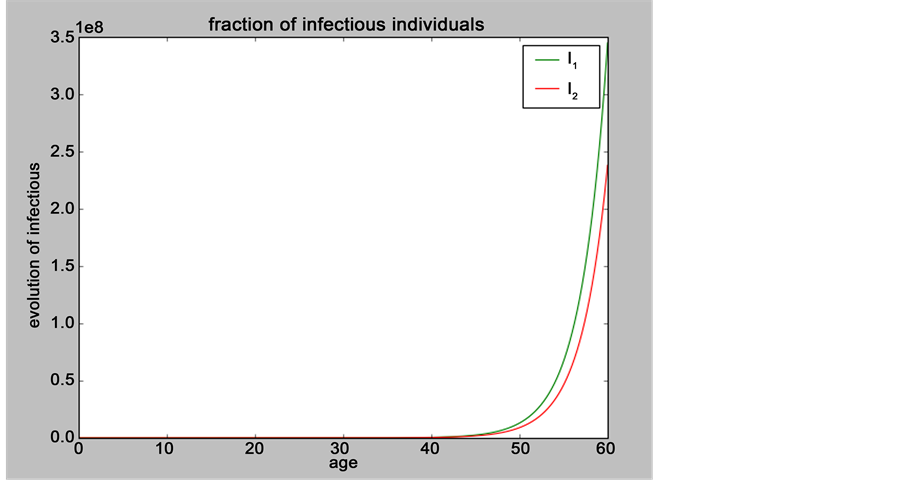
5.4. Simulation
In this section, when 
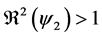
Figure 2. Evolution of the number of latents individuals with 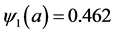

Figure 3. Evolution of the number of latents individuals with 

Figure 4. Evolution of the number of infectious individuals when: 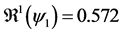
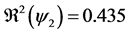
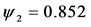
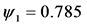
When 



6. Discussion, Conclusion and Future Work
In this paper, an age structured model of two-patch for tuberculosis was analyzed and discussed. Each sub-population is subjected to a vaccination program. Apart from age; the vaccinated compartment, we introduced as a class of treated in the model proposed by Tewa J. Jules in [11] and allowed the migration of vaccinated population. The same result was found if the most susceptible migrated too. Although some studies have shown an ineffectiveness of BCG in the prevention of tuberculosis [21] , our work demonstrated the contribution of BCG in the process of eradicating TB. The negative impact of the increase in the birth rate was shown. If we neglect the mortality death rate linked to the disease, we obtain the only usual condition of global stability to the disease free equilibrium i.e.
Acknowledgements
We thank the Editor and the referee for their comments. We would like to thank Numerical Analysis student group for their valuable comments and the authors whose works have been used in this article. We also thank the ministry of Higher Education of Research an Innovation who kindly supported the costs of the publication.
Cite this paper
Wahid, B.K.A. and Bisso, S. (2016) Mathematical Analysis and Simulation of an Age-Structured Model of Two-Patch for Tuberculosis (TB). Applied Mathematics, 7, 1882-1902. http://dx.doi.org/10.4236/am.2016.715155
References
- 1. Rohaeti, E., Wardatun, S. and Andriyati, A. (2015) Stability Analysis Model of Spreading and Controlling of Tuberculosis. Applied Mathematical Sciences, 9, 2559-2566.
http://dx.doi.org/10.12988/ams.2015.52100 - 2. Silva, C.J. and Torres, D.F.M. (2015) A TB-HIV/AIDS Coinfection Model and Optimal Control Treatment. Discrete and Continuous Dynamical Systems, 35, 4639-4663.
http://dx.doi.org/10.3934/dcds.2015.35.4639 - 3. Echeng, B.B. and Lebedev, K.A. (2015) On Mathematical Modeling of the Effect of Bi-Therapeutic Treatment of Tuberculosis Epidemic. Journal of Modern Mathematics and Statistics, 9, 1-7.
- 4. Raoult, D. (2006) Epidémie et maladies infectieuse dans l’histoire.
- 5. World Health Organization (2005) Global Tuberculosis Control: Surveillance, Planning, Financing. WHO/HTM/TB/2005, Geneve, 349.
- 6. Patel, A., Siskind, F.V., Abrahams, E. and Parker, J. (1991) Case-Control Evaluation of a School-Age BCG Vaccination Programme in Subtropical Australia. Bulletin of the World Health Organization, 69, 425-433.
- 7. Zwerling, A., Shrestha, S. and David, W.D. (2015) Mathematical Modeling and Tuberculosis Advances in Diagnostics and Novel Therapies. Advances in Medicine, 2015, Article ID: 907267.
- 8. Chavez, C.C. and Feng, Z. (1998) Global Stability of an Age-Structure Model for TB and Its Applications to Optimal Vaccination Strategies. Mathematical Biosciences, 151, 135-154.
http://dx.doi.org/10.1016/S0025-5564(98)10016-0 - 9. Chavez, C.C., Hethcotte, H.W., Andreasen, V., Levin, S.A. and Liu, W.M. (1989) Epidemiological Models with Age Structure, Proportionate Mixing, and Cross-Immunity. Journal of Mathematical Biology, 27, 233-258.
http://dx.doi.org/10.1007/BF00275810 - 10. Agusto, F.B., Cook, J., Shelton, P.D. and Wickers, M.G. (2015) Mathematical Model of MDR-TB and XDR-TB with Isolation and Lost to Follow-Up. Abstract and Applied Analysis, 2015, Article ID: 828461.
http://dx.doi.org/10.1155/2015/828461 - 11. Tewa, J.J., Bowong, S. and Mewoli, B. (2012) Mathematical Analysis of Two-Patch Model for the Dynamical Transmission of Tuberculosis. Applied Mathematical Modelling, 36, 2466-2485.
http://dx.doi.org/10.1016/j.apm.2011.09.004 - 12. Tewa, J.J., Bowong, S., Mewoli, B. and Kurths, J. (2011) Two-Patch Transmission of Tuberculosis. Mathematical Population Studies, 18, 189-205.
http://dx.doi.org/10.1080/08898480.2011.596757 - 13. Zhang, J. and Feng, G. (2015) Global Stability for a Tuberculosis Model with Isolation and Incomplete Treatment. Computation and Applied Mathematics, 34, 1237-1249.
http://dx.doi.org/10.1007/s40314-014-0177-0 - 14. Moualeu, D.P., Bowong, S., Tewa, J.J. and Emvudu, Y. (2012) Analysis of the Impact of Diabetes on the Dynamical Transmission of Tuberculosis. Mathematical Modelling of Natural Phenomena, 7, 117-146.
http://dx.doi.org/10.1051/mmnp/20127309 - 15. Greenhalgh, D. (1988) Threshold and Stability Results for an Epidemic Model with an Age-Structured Meeting Rate. IMA Journal of Mathematics Applied in Medicine and Biology, 5, 81-100.
http://dx.doi.org/10.1093/imammb/5.2.81 - 16. Dietz, K. and Schenzle, D. (1985) Proportionate Mixing Models for Age-Dependent Infection Transmission. Journal of Mathematical Biology, 22, 117-120.
http://dx.doi.org/10.1007/BF00276550 - 17. Zou, L., Ruan, S. and Zhang, W. (2010) An Age-Struvtured Model for the Transmission Dynamics of Hepatitis B. SIAM Journal on Applied Mathematics, 70, 3121-3139.
http://dx.doi.org/10.1137/090777645 - 18. Webb, G.F. (2008) Population Models Structured by Age, Size, and Spatial Position. In: Magal, P. and Ruan, S., Eds., Structured Population Models in Biology and Epidemiology, Springer-Verlag, Berlin, 1-49.
http://dx.doi.org/10.1007/978-3-540-78273-5_1 - 19. Inaba, H. (2006) Mathematical Analysis of an Age-Structured SIR Epidemic Model with Vertical Transmission. Discrete and Continuous Dynamical Systems Series B, 6, 69-96.
http://dx.doi.org/10.3934/dcdsb.2006.6.69 - 20. Djidjou, R.D., Tewa, J.J. and Bowong, S. (2014) Analysis of an Age-Structured SIL Model. With Demographics Process and Vertical Transmission. ARIMA Journal, 17, 23-52.
- 21. Saylers, A.A. and Whitt, D.D. (1994) Bacterial Pathogenesis: A Molecular Approach. ASM, Washington DC.