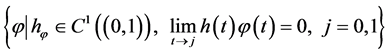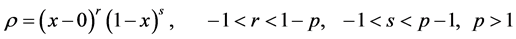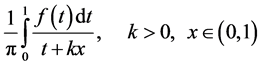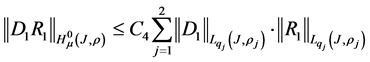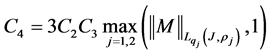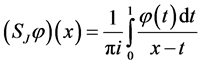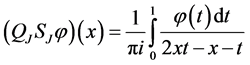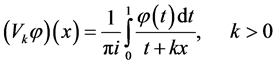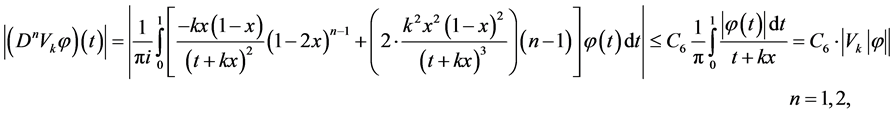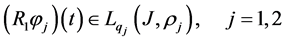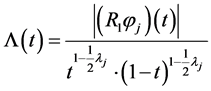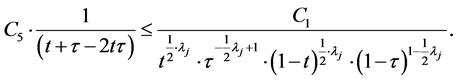Received 11 August 2014; revised 30 August 2014; accepted 8 September 2014

ABSTRACT

In this paper we consider operators with endpoint singularities generated by linear fractional Carleman shift in weighted Hölder spaces. Such operators play an important role in the study of algebras generated by the operators of singular integration and multiplication by function. For the considered operators, we obtained more precise relations between norms of integral operators with local singularities in weighted Lebesgue spaces and norms in weighted Hölder spaces, making use of previously obtained general results. We prove the boundedness of operators with linear fractional singularities.

Keywords:

Endpoint Singularities, Weighted Holder Space, Weighted Lebesgue Spaces, Relation between Norms, Boundedness

1. Introduction

The solvability theory of singular integral operators has developed independently in Hölder and Lebesgue spaces [1] -[7] , as norms in these spaces differ widely in their structure.

The norm in weighted Hölder spaces is defined in the following way. A function 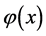that satisfies the following condition on contour,

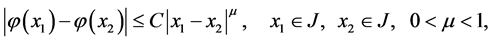
is called Hölder function with exponent and constant C on contour J.

Let J be a power function which has zeros at the endpoints:

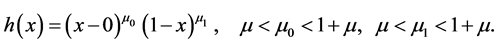
The functions that become Hölder functions and turn into zero at the endpoints, after being multiplied by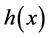, form a Banach space of Hölder functions with weight h:

,.

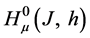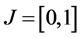The norm in space is defined by

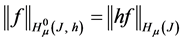
where

and

,

,

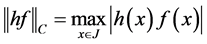specifying that

.

We denote by 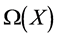the set of all bounded linear operators mapping the Banach space into.

The norm of an operator will be denoted by.

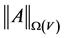
We denote a class of continuous functions on the segment by, also denote a class of differentiable functions on interval by, and we denote by a class of functions

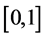
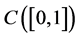
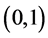
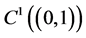
Let us introduce the following notation:

,

is the identity operator, ,; is the characteristic function of segment,.

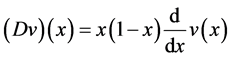
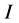
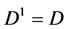
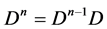
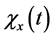
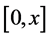
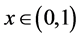
Let be a power function which has zeros at the endpoints x = 0, x = 1:

Let denote the space of functions on J which are integrable in the -th power after multiplication by the weight-function.

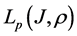
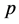
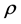
The norm in space is defined by

.

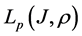
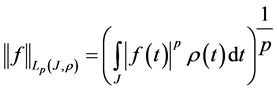
As we can see, the norms in spaces and are different in their character, and the presence of a direct connection should not be expected. However, in this work, we describe a class of operators with local singularities for which we were able to find inequalities that connect the norms in weighted Lebesgue spaces with the norms in weighted Hölder spaces. Operators with fixed singularities perform an essential role in the study of singular integral operators with shift [8] -[10] , in particular in the construction of regularizations.

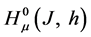
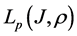
By way of representatives of such types of operators we may consider the following operators with local singularities:

,

Such operators can be used in the study of boundedness, of belonging of some operators to Banach algebras and of the solvability of operators in weighted Hölder spaces, on the basis of known results for operators in weighted Lebesgue spaces.

2. Inequality Which Connects the Norms in Lebesque and Hölder Weighted Spaces

It is useful to avoid two variables in the second term of the definition of the norm in Hölder spaces, for which we make use of

Lemma 1.

Let

,

then

,

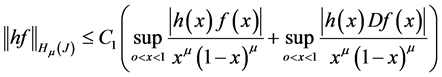
where is a constant which does not depend on.

On the basis of Lemma 1 the following theorem can be proved [11] .

Theorem 1.

Let the following conditions hold for some operator:

1) Operators are bounded in spaces

;

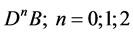
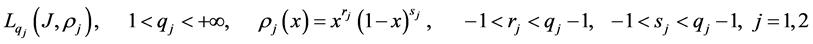
2) For any fixed and for any function from space,

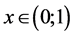
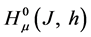
the following properties are fulfilled:

(1)

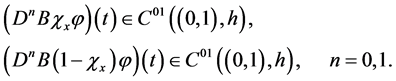
Moreover, inequalities

(2)

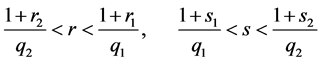
are correct.

It follows that operator is bounded in space and for its norm the following estimation is fulfilled

, (3)

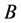
where is a certain positive constant.

These results can be used in the study of operators in weighted Hölder spaces, on the basis of known results for operators in weighted Lebesgue spaces. In particular, operators with local endpoint singularities can be used in the construction of the left and the right regularizers in the study of Fredholmness of operators in weighted Hölder spaces.

3. Operators with Linear Fractional Endpoint Singularities

We formulate a useful assertion which follows directly from Theorem 1.

Corollary 1. Let properties (1) and (2) be correct for the operator and furthermore

(4)

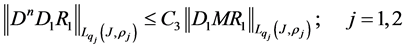
Here is an operator that may be not linear; is a positive constant; the operators, and are bounded in spaces,.

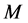
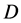
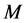
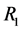
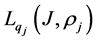
Then

where

We consider the operators

,

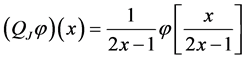
and

We note that for operators and conditions (1), (2), (4) of corollary 1 are fulfilled.

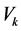
Moreover, the following estimations hold

(5)

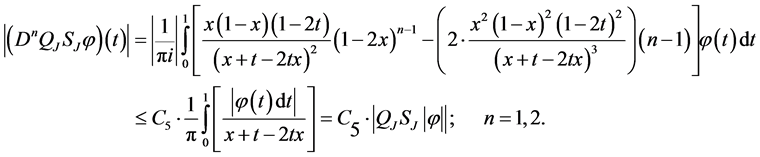
where

,

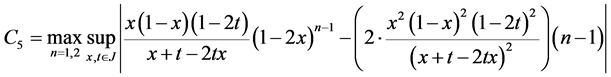
and

where

.

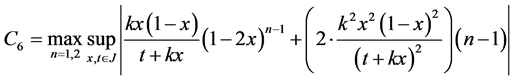
Theorem 2. Let an operator be bounded in the space

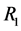
and inequalities (2) be true.

If

, (6)

then the operators and are bounded in space.

Proof. Let a function belong to.

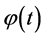
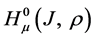
We introduce functions

and

.

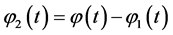
From the fact that

It follows that the function

is summable on segment if

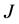
and

.

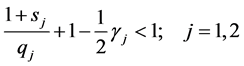
Condition (6) of the theorem makes it possible to choose constants and from interval so that

.

Now, we carry out an estimation of the expression.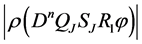

In doing so, we will use inequalities (5),

where

.

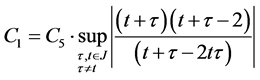
Here we have taken into account that

Since

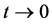
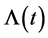
when; and since function is summable, it follows that conditions (1) of Theorem 1 are fulfilled for the operator.

From properties (5), condition (4) follows:

,

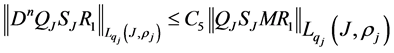
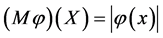
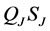
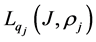
where, and as the operator is bounded in it follows that all conditions

of Corollary 1 are fulfilled and we can apply it. Therefore operator is bounded in.

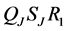
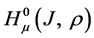
Since operator is bounded in, the boundness of operator in may be proved analogously.

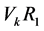
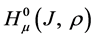
References

NOTES

^*Corresponding author.