Received 7 October 2014; revised 28 October 2014; accepted 10 November 2014

ABSTRACT

In this paper, we use the mappings with quasi-contractive conditions, defined on a partially ordered set with cone metric structure, to construct convergent sequences and prove that the limits of the constructed sequences are the unique (common) fixed point of the mappings, and give their corollaries. The obtained results improve and generalize the corresponding conclusions in references.

Keywords:

Common Fixed Point, Cone Metric Space, Complete

1. Introduction

Huang and Zhang [1] recently have introduced the concept of cone metric spaces and have established fixed point theorems for a contractive type map in a normal cone metric space. Subsequently, some authors [2] -[7] have generalized the results in [1] and have studied the existence of common fixed points of a finite self maps satisfying a contractive condition in the framework of normal or non-normal cone metric spaces. On the other hand, some authors discussed (common) fixed point problems for contractive maps defined on a partially ordered set with cone metric structure [8] -[13] . These results improved and generalized many corresponding (common) fixed point theorems of contractive maps on cone metric spaces. Here, we will obtain (common) fixed point theorems of maps with certain quasi-contractive conditions on a partially ordered set with cone metric structure.

Let E be a real Banach space. A subset P₀ of E is called a cone if and only if:

i) P₀ is closed, nonempty, and;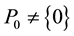

ii)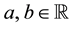, 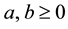and 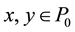implies;

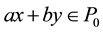iii).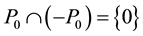

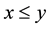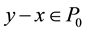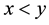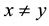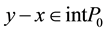Given a cone, we define a partial ordering ≤ on E with respect to P₀ by if and only if. We will write to indicate that but, while will stand for (interior of P₀).

The cone P₀ is called normal if there is a number 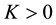such that for all,

.

The least positive number K satisfying the above is called the normal constant of P₀. It is clear that.

In the following we always suppose that E is a real Banach space, P₀ is a cone in E with and ≤ is a partial ordering with respect to P₀.

Let X be a nonempty set. Suppose that the mapping satisfies

d1) for all and if and only if;

d2) for all;

d3), for all.

Then d is called a cone metric on X, and is called a cone metric space.

Let be a cone metric space. We say that a sequence in X is

e) Cauchy sequence if for every with, there is an N such that for all n, m > N,;

g) convergent sequence if for every with, there is an N such that for all such that for some. Let or.

is said to be complete if every Cauchy sequence in X is convergent in X.

Let be a cone metric space, and. f is said to be continuous [13] at x₀ if for any sequence, we have.

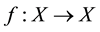
Lemma 1 [14] Let be a cone metric space. Then the following properties hold:

1) if and, then; if for all, then;

2) if where and, then.

Lemma 2 [15] Let be a cone metric space, a sequence in X and a sequence in P₀ and. If for any, then is Cauchy.

2. Main Results

At first, we give an example to show that there exists a self-map f on a partially ordered set such that for each there exists y satisfying and.

Example Let be a real space. Define by

Then obviously, for each, there exists satisfying and.

is said to be a partially order-cone metric space if is a partially ordered set and is a cone metric space.

Theorem 1 Let be a complete partially ordered-cone metric space. Suppose that a map is continuous and the following two assertions hold:

i) there exist A, B, C, D, E ≥ 0 with and for with, such that

;

ii) for each, there exists such that and.

Then f has a fixed point. Furthermore, if any two elements x and y in are comparative and, then f has a unique fixed point in X.

Proof Take any, then by ii), we obtain a sequence as follows: for all and.

For any fixed, since, by i),

so,.

Let, then by i) and

.

Repeating this process,

.

Let, then from the above,

.

Obviously, and as since So for all, hence is a Cauchy sequence by Lemma 2 and there exists such that by the completeness of X. Since f is continuous and, so, i.e., is a fixed point of f.

If and are all fixed points of f and suppose that, then by i),

Hence by (2) in Lemma 1, so is the unique fixed point of f.

Another version of Theorem 1 is following:

Theorem 2 Let be a complete partially ordered-cone metric space. Suppose that is continuous and the following two assertions hold:

i) there exist with and for all with,

;

ii) for each, there exists such that and.

Then f has a fixed point. Furthermore, if x and y is comparative for all, then f has an unique fixed point in X.

Proof Take, and, then the conclusion is true by Theorem 1.

From now, we give common fixed point theorems for a pare of maps.

Theorem 3 Let be a complete partially ordered-cone metric space. If are two maps such that f or g is continuous and the following two assertions hold:

i) there exist A, B, C, D, E ≥ 0 with, and such that for all comparative;

ii) for each, there exist such that, and,.

Then f and g have a common fixed point. Furthermore, if x and y in are comparative and, then is singleton.

Proof Take any element, then using ii), we can construct a sequence satisfying the following condition, for all, and.

For any, by i), we have

hence

where. And

hence

where.

Let, then by i), and by induction, for any

For any with,

where. Similarly,

So for any with m > n > 0, there exists with, that is, such that

.

Obviously, and as since. So for all, hence is Cauchy by Lemma 2 and there exists such that.

Suppose that f is continuous, then since. For there exists such that and by ii). By i),

So by (2) in Lemma 1, hence. Therefore. Similarly, we can give the same result for the case of g being continuous.

If then and are comparative, hence by i),

so by (2) in Lemma 1. Hence.

Modifying the idea of Zhang [16] , we obtain next three corollaries.

Corollary 1 The conditions of A, B, C, D, E in i) of Theorem 3 can be replaced by the following:

i') there exist A, B, C, D, E ≥ 0 and such that, , , ,.

Proof Since so

,

hence therefore

.

Corollary 2 The conditions of A, B, C, D, E in i) of Theorem 3 can be replaced by the following:

i'') there exist A, B, C, D, E ≥ 0 such that A + B + C + D + E = 1, C > B and D > E or C < B and D < E.

Proof Take such that and, and let. Then the following holds: for all comparative elements,

.

Obviously, A', B, C, D, E satisfy i') in Corollary 1.

Corollary 3 The conditions of 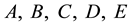in 1) of Theorem 3 can be replaced by the following:

i''') there exist A, B, C, D, E ≥ 0 such that and or.

Proof Since, so, hence

,

or

,

which implies that

,

or

.

If or, then the above two relations reduce

.

The following is a non-continuous version of Theorem 3.

Theorem 4 Let be a complete partially ordered-cone metric space. If are maps such that i) and ii) in Theorem 3 hold and iii) or iv) holds

iii) if an increasing sequence converges to, then and for all and;

iv) if an increasing sequence converges to, then and for all and.

Then f and g have a common fixed point. Furthermore, if x and y in are comparative and, then is singleton.

Proof By i) and ii) in Theorem 3, we construct a sequence such that, , for all, and and.

Case I: Suppose iv) holds, then and for all and. By i),

so we obtain

,

where and Since, for any there exist enough large such that and for all, hence

,.

So by (1) in Lemma 1, hence.

For there exists such that and by ii). Hence by i),

so by (2) in Lemma 1. Hence, i.e.,.

Case II: Suppose iii) holds, then and for all and. By (1),

so we obtain

,

where and Since, for any there exist enough large such that and for all, hence ,. So by (1) in Lemma 1, that is,.

For there exists such that and by ii). Hence by i),

so by (1) in Lemma 1. Hence, i.e.,.

So in any case, The uniqueness is obvious.

Remark 1 We can also modify Corollary 1 - 3 to give the corresponding corollaries of Theorem 4, but we omit the part.

Remark 2 In this paper, we discuss the common fixed point problems for mappings with quasi-contractive type (i.e., expansive type) on partially ordered cone metric spaces, but some authors in references discussed the same problems for contractive or Lipschitz type. So our results improve and generalize the corresponding conclusions.

Cite this paper

HailanJin,YongjiePiao, (2014) Fixed Points and Common Fixed Points of Quasi-Contractive Mappings on Partially Ordered-Cone Metric Spaces. Applied Mathematics,05,3437-3444. doi: 10.4236/am.2014.521321

References