Applied Mathematics
Vol.05 No.10(2014), Article ID:46526,11 pages
10.4236/am.2014.510145
A closed-form solution of a kinetic integral equation for rarefied gas flow in a cylindrical duct
Carmo Henrique Kamphorst1, Patricia Rodrigues2, Liliane Basso Barichello3
1Departamento de Ciências Exatas e da Terra, Universidade Regional Integrada do Alto Uruguai e das Missões (URI), Frederico Westphalen, Brazil
2Departamento de Ciências Agronômicas e Ambientais, Universidade Federal de Santa Maria (UFSM), Frederico Westphalen, Brazil
3Instituto de Matemática, Universidade Federal do Rio Grande do Sul (UFRGS), Porto Alegre, Brazil
Email: carmo@edu.uri.br, patricia@ufsm.br, lbaric@mat.ufrgs.br
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 March 2014; revised 25 April 2014; accepted 2 May 2014
ABSTRACT
A spectral method based on Hermite cubic splines expansions combined with a collocation scheme is used to develop a solution for the vector form integral S-model kinetic equation describing rarefied gas flows in cylindrical geometry. Some manipulations are made to facilitate the computational treatment of the singularities inherent to the kernel. Numerical results for the simulation of flows generated by pressure and thermal gradients, Poiseuille and thermal-creep problems, are presented.
Keywords:
Rarefied gas dynamics, integral equation, S-model, collocation schemes

1. Introduction
Research in the field of rarefied gas dynamics (RGD) involving the analysis and description of micro and nanoflows has been fundamental for the development of micro devices and new technologies, specially in the field of micro-electro-mechanical systems (MEMS) [1] -[5] .
The Boltzmann equation is the fundamental mathematical model for dealing with problems in RGD [6] . Investigations of its solution and associated kinetic models have found much attention in the last few years [7] - [13] . Numerical and analytical approaches have been developed, mainly in Cartesian coordinates [14] [15] .
The solution of Boltzmann-like problems is even more challenging in multidimensional and complex geome- tries, particularly, if one seeks for analytical approaches. In cylindrical coordinates, to overcome such difficulties, the integral form of the kinetic equations has been employed. In this context, several approaches have been proposed in the past years [16] - [19] , particularly related to the solution of the BGK model [20] , as, for example, the use of classical Legendre polynomials expansions [21] . A special approach used in an earlier work of Ferziger [22] , is based on a transformation proposed by Mitsis [23] , which allows us to recast the problem in cylindrical coordinates into a much simpler problem in plane Cartesian coordinates. The transformation, however, is restricted to some specific (simpler) physical cases.
Mitsis’ transformation [23] was used by Siewert and Valougeorgis [24] to develop a solution for the integral form of the S-model [25] kinetic equation, which is a vector equation, while the BGK kinetic equation is a scalar problem. It has been addressed in the literature, however, that the S-model is more appropriate than the BGK model to deal, for instance, with nonisothermal flows [24] [26] .
In this work, we use an spectral approach based on Hermite cubic splines expansions along with a collocation scheme to solve the vector integral form of the S-model kinetic equation for flow in cylindrical tube. Numerical results are obtained for the Poiseuille and thermal-creep problems. As in other analytical approaches [24] the solution is explicit, in terms of the spatial variable. However, the technique proposed in this work, that has been also effective to deal with the BGK integral equation [27] , may be extended to deal with the problems which include reflexive boundary conditions.
2. The formulation
The initial formulation of the problems we treat in this work, is the integro-differential formulation associated with the kinetic S-model [24] , for describing the behavior of gas flows in a cylindrical tube of radius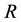 , with no variation in the axial direction, such that the distribution of particles and the boundary conditions depends on the spatial variable
, with no variation in the axial direction, such that the distribution of particles and the boundary conditions depends on the spatial variable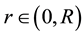 , written in dimensionless units, and the particle velocity vector
, written in dimensionless units, and the particle velocity vector , also given in dimensionless units, expressed in the cylindrical coordinates. Still, in the initial formulation, the flow is subject to reflexive boundary conditions at
, also given in dimensionless units, expressed in the cylindrical coordinates. Still, in the initial formulation, the flow is subject to reflexive boundary conditions at . In Ref. [24] , the authors follow a previous derivation regarding to the BGK model [28] to derive in details the integral form of the equation for the S-model, which describes the flow of a rarefied gas in a straight cylindrical duct of radius
. In Ref. [24] , the authors follow a previous derivation regarding to the BGK model [28] to derive in details the integral form of the equation for the S-model, which describes the flow of a rarefied gas in a straight cylindrical duct of radius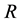 , which will be our starting point of this work. Since the derivations were done in details in [24] [28] , we do not repeat it here. We start, already, from considering the integral vector equation [24]
, which will be our starting point of this work. Since the derivations were done in details in [24] [28] , we do not repeat it here. We start, already, from considering the integral vector equation [24]
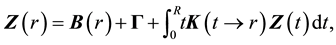 (1)
(1)
for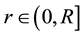 . In Equation (1) the inhomogeneous term
. In Equation (1) the inhomogeneous term  is given by
is given by
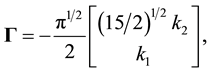 (2)
(2)
where the constants 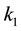 and
and 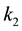 are defined so that
are defined so that 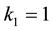 and
and 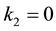 for the so-called problem of Poiseuille flow while
for the so-called problem of Poiseuille flow while 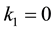 and
and 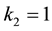 for the thermal-creep problem. Still, the kernel of integral equation is
for the thermal-creep problem. Still, the kernel of integral equation is
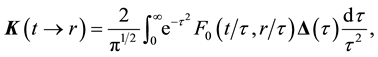 (3)
(3)
where

and

Here 


with


and

Now, if we define [24] ,

we can evaluate the quantities of physical interest for the gas flow, such as the velocity profile [24]

and the heat-flow profile

Consequently, we write the particle-flow rate as

and the heat-flow rate

The Equations (11) to (14) are used for both problems, Poiseuille and thermal-creep, depending on the specified values of the constants 

Finally, we note that, in Equation (1), the term 

3. The solution
Firstly, we rewrite Equation (1) as,

for


We then propose a solution to Equation (15) in terms of a truncated expansion of Hermite cubic splines functions [30] , as

where 

whose components (constants) 


first of all, we consider there to be 


(see Appendix for details).
If we now substitute Equation (16) into Equation (15) we obtain

which still can be expressed in the form

with

and

At this point, we introduce a collocation scheme, such that, if we evaluate Equation (19) at the collocation points

we end up with

for



given by Equation (16).
4. Computational Aspects
The procedure described in Section 3 may be considered quite straightforward. However the solution of the
linear system given by Equations (23), depends on the explicit evaluation of the integrals 

that introduce numerical difficulties. In this way, a series of computational steps have to be taken into account.
As a first step, as used in previous works [24] [31] , for computational reasons, the modified Bessel functions are rewritten as

such that Equations (4) and (5) are now expressed as

for 

for

Continuing, if we look back to Equations (6) to (9), we can see that

with


and

where, again, the (constant components) matrices



Finally, for future use, later on in this text, we can also express the kernel of the integral equation, in a matrix form,

following, of course, the previous definitions given in Equations (7) to (9) and Equations (29) to (31). Here,


and

Going back to the definition of the linear system we need to solve, Equations (23), we now focus our
attention in the definition of the functions 

Considering that 


we note that

if 

if 

In an analogous form,

if 

if 

In fact, to be more specific, we can express the vector

such that

and

where 





if 

if


with

and

Here

if 

if

and

for

for


(50)-(51). Still, the terms 



and

depending on the problem, as mentioned earlier: 



The linear system given by Equations (52) and (53), is of order 




and the heat flow profile

Numerical quadrature schemes
Searching for a general procedure, as much as possible, the basic approach for evaluating the integrals involved in this derivation was based on the use of the Gauss-Legendre quadrature scheme [29] with nodes 


In this way, we define

and we consider a quadrature scheme with 


and

At this point, however, a special remark has to be done in regard to the evaluation of Equation (60). While
the general procedure described above works well as long as 
one obtains results which agree in seven digits with results obtained by the software Maple―the case 
To deal with that, we subtract (and add) from Equation (29) the expression

In the resulting integral expression, we introduce the change of variables

and, subsequently, once more, we add (and subtract) the integral term

To be clear, when 



with

and

The reasons for doing that is, firstly, the use of these additional functions results in a smoother function when approaching


where 





Therefore, in regard to the computational scheme, we note that 


To all other integrations processes needed in this formulation, more specifically, the expressions given by Equations (46) and (51) as well as Equations (13) and (14), linear mappings from the integration interval to the interval 

if 

if


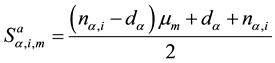
and

With this, we conclude the evaluation of the elements of the system given by Equations (52) and (53).
5. Numerical results
As input data in our program we need to specify the radius of the duct, 



As a first test, to check and to have confidence in our approach, we reproduced all the results listed in Ref. [24] , for the velocity and heat-flow profiles (case



As we mentioned earlier, the approach used in that work can be very accurate, since it works with a Cartesian coordinates problem associated with a very accurate discrete ordinates solution, after using Mitsis’ transfor- mation [23] . In order to get agreement in six to seven digits, for all cases, with Siewert and Valougeorgis’ results
(listed with seven digits) [24] , we used










We then investigated additional cases. To provide the results we list in Table 1 and Table 2, we used the first set of parameters listed above. In regard to Table 2, we remark that, the Onsager reciprocity relation [33] [34] , 
Table 1. Velocity and heat flow profiles in a duct with R = 1.
Table 2. Flow rates.
declared in that paper (0.5%). In addition to provide accurate results, it is important to remark that, the approa- ch proposed in this work may be used to simulate the case which includes specular reflection at the surface
6. Conclusion
In this work, we have used a classical spectral approach, based on the use of Hermite cubic splines combined with a collocation scheme, to obtain a solution, in a closed-form, to the S-model kinetic integral vector equation relevant to describe rarefied gas flow in cylindrical coordinates. The main purpose of this work was to verify the performance of this approach as an extension of an earlier work related to a simpler integral model equation, the BGK model, trying to derive, as much as possible, a general approach which can be now, in a subsequent work, extented to include the treatment of reflexive boundary conditions. The numerical results obtained showed good agreement with accurate results available in the literature.
Acknowledgements
The authors would like to thank CNPq of Brazil for partial financial support of this work. One of the authors (LBB) would like to thank the Mathematics Department of North Carolina State University for the kind hospitality during a visit when this work was written.
References
- Karniadakis, G., Beskok, A. and Aluru, N. (2005) Microflows and Nanoflows. Springer, New York.
- Kakaç, S., Vasiliev, L.L., Bayazitoglu, Y. and Yener, Y. (2005) Microscale Heat Transfer: Fundamentals and Applications. Springer, New York. http://dx.doi.org/10.1007/1-4020-3361-3
- Li, D. (2008) Micro and Nanoscale Gas Dynamics. Springer, New York.
- Wang, M., Lan, X. and Li, Z. (2008) Analyses of Gas Flows in Micro- and Nanochannels. International Journal of Heat and Mass Transfer, 51, 3630-3641. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2007.10.011
- Gad-el-Hak, M. (2005) The MEMS Handbook. Mechanical Engineering Handbook Series, CRC Press, New York.
- Cercignani, C. (1988) The Boltzmann Equation and Its Applications. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-1039-9
- Sone, Y., Ohwada, T. and Aoki, K. (1989) Evaporation and Condensation on a Plane Condensed Phase: Numerical Analysis of the Linearized Boltzmann Equation for Hard-Sphere Molecules. Physics of Fluids A, 1, 1398-1405. http://dx.doi.org/10.1063/1.857316
- Sharipov, F. and Seleznev, S. (1998) Data on Internal Rarefied Gas Flows. Journal of Physical and Chemical Reference Data, 27, 657-706. http://dx.doi.org/10.1063/1.556019
- Williams, M.M.R. (2001) A Review of the Rarefied Gas Dynamics Theory Associated with Some Classical Problems in Flow and Heat Transfer. Zeitschrift für Angewandte Mathematik und Physik, 52, 500-516. http://dx.doi.org/10.1007/PL00001558
- Barichello, L.B., Camargo, M., Rodrigues, P. and Siewert, C.E. (2001) Unified Solutions to Classical Flow Problems Based on the BGK Model. Zeitschrift für Angewandte Mathematik und Physik, 52, 517-534. http://dx.doi.org/10.1007/PL00001559
- Barichello, L.B. and Siewert, C.E. (2003) Some Comments on Modeling the Linearized Boltzmann Equation. Journal of Quantitative Spectroscopy and Radiative Transfer, 77, 43-59. http://dx.doi.org/10.1016/S0022-4073(02)00074-2
- Siewert, C.E. (2003) The Linearized Boltzmann Equation: Concise and Accurate Solutions to Basic Flow Problems. Zeitschrift für Angewandte Mathematik und Physik, 54, 273-303. http://dx.doi.org/10.1007/s000330300005
- Scherer, C.S., Prolo Filho, J.F. and Barichello, L.B. (2010) An Analytical Approach to the Unified Solution of Kinetic Equations in the Rarefied Gas Dynamics. I. Flow Problems. Zeitschrift für Angewandte Mathematik und Physik, 60, 70-115. http://dx.doi.org/10.1007/s00033-008-7084-4
- Sone, Y. (2002) Kinetic Theory and Fluid Dynamics. Birkhäuser, Boston. http://dx.doi.org/10.1007/978-1-4612-0061-1
- Ivchenko, I.N., Loyalka, S.K. and Tompson, R.V. (2007) Analytical Methods for Problems of Molecular Transport. Springer, New York. http://dx.doi.org/10.1007/978-1-4020-5865-3
- Lang, H. and Loyalka, S.K. (1984) Some Analytical Results for Thermal Transpiration and the Mechanocaloric Effect in a Cylindrical Tube. Physics of Fluids, 27, 1616-1619. http://dx.doi.org/10.1063/1.864817
- Valougeorgis, D. and Thomas Jr., J.R. (1986) Exact Numerical Results for Poiseuille and Thermal Creep Flow in a Cy- lindrical Tube. Physics of Fluids, 29, 423-429. http://dx.doi.org/10.1063/1.865725
- Siewert, C.E. (2000) Poiseuille and Thermal-Creep Flow in a Cylindrical Tube. Journal of Computational Physics, 160, 470-480. http://dx.doi.org/10.1006/jcph.2000.6464
- Loyalka, S.K. and Tompson, R.V. (2009) The Velocity Slip Problem: Accurate Solutions of the BGK Model Integral Equation. European Journal of Mechanics-B/Fluids, 28, 211-213. http://dx.doi.org/10.1016/j.euromechflu.2008.08.001
- Bhatnagar, P.L., Gross, E.P. and Krook, M. (1954) A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Physical Review, 94, 511-525. http://dx.doi.org/10.1103/PhysRev.94.511
- Rodrigues, P., Kamphorst, C.H. and Barichello, L.B. (2009) A Spectral Method for Rarefied Gas Dynamics Problems in Cylindrical Geometry. International Journal of Pure and Applied Mathematics, 51, 181-187.
- Ferziger, J.H. (1967) Flow of a Rarefied Gas through a Cylindrical Tube. Physics of Fluids, 10, 1448-1453. http://dx.doi.org/10.1063/1.1762304
- Mitsis, G.J. (1963) Transport Solutions to the Monoenergetic Critical Problems. Argonne National Laboratory, Argonne, Illinois, Report ANL-6787, 370-382.
- Siewert, C.E. and Valougeorgis, D. (2002) An Analytic Discrete-Ordinates Solution of the S model in Rarefied Gas Dinamics: Poiseuille and Thermal-Creep Flow in a Cylindrical Tube. Journal of Quantitative Spectroscopy and Radia- tive Transfer, 72, 531-550.
- Shakhov, E.M. (1974) Method of Investigation of Rarefied Gas Flows. Nauka, Moscow.
- Sharipov, F. (1996) Rarefied Gas Flows through a Long Tube at Any Temperature Ratio. Journal of Vacuum Science & Technology A, 14, 2627-2635. http://dx.doi.org/10.1116/1.579991
- Kamphorst, C.H., Rodrigues, P. and Barichello, L.B. (2009) A Spectral Approach to Compute Rarefied Gas Flows in Cylindrical Geometry. International Nuclear Atlantic Conference, Rio de Janeiro, 27 September-2 October 2009. (CD-Rom)
- Barichello, L.B., Camargo, M., Rodrigues, P. and Siewert, C.E. (2002) An Integral Equation Basic to the BGK Model for Flow in a Cylindrical Tube. Zeitschrift für angewandte Mathematik und Physik, 53, 769-781. http://dx.doi.org/10.1007/s00033-002-8182-3
- Abramowitz, M. and Stegun, I.A. (1965) Handbook of Mathematical Function. Dover Publications, New York.
- Schultz, M.N. (1973) Spline Analysis. Prentice Hall, Englewood Cliffs.
- Barichello, L.B., Rodrigues, P. and Siewert, C.E. (2002) An Analytical Discrete-Ordinates Solution for Dual-Mode Heat Transfer in a Cylinder. Journal of Quantitative Spectroscopy and Radiative Transfer, 73, 583-602. http://dx.doi.org/10.1016/S0022-4073(01)00181-9
- Dongarra, J.J., Bunch, J.R., Moler, C.B. and Stewart, G.W. (1979) LINPACK User’s Guide. SIAM, Philadelphia. http://dx.doi.org/10.1137/1.9781611971811
- Sharipov, F. (1994) Onsager-Casimir Reciprocity Relations for Open Gaseous Systems at Arbitrary Rarefaction. I. General Theory for Single Gas. Physica A, 203, 437-456. http://dx.doi.org/10.1016/0378-4371(94)90009-4
- Sharipov, F. (1994) Onsager-Casimir Reciprocity Relations for Open Gaseous Systems at Arbitrary Rarefaction. II. Application of the Theory for Single Gas. Physica A, 203, 457-485. http://dx.doi.org/10.1016/0378-4371(94)90010-8
Appendix
The Spline Functions
We follow here the Hermite cubic splines functions as defined by Schultz [30]. In this way, we first consider the 



where, in this work, we use



where 




for


and we consider that the spline functions are zero unless otherwise, to write


for

Similarly, we write


for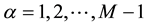
 (86)
(86)




