Applied Mathematics
Vol.5 No.8(2014), Article ID:45707,15 pages DOI:10.4236/am.2014.58117
Five Steps Block Predictor-Block Corrector Method for the Solution of 
Mathew Remilekun Odekunle1, Michael Otokpa Egwurube1, Adetola Olaide Adesanya1, Mfon Okon Udo2
1Department of Mathematics, Modibbo Adama University of Technology, Yola, Nigeria
2Department of Mathematics and Statistics, Cross River University of Technology, Calabar, Nigeria
Email: mfudo4sure@yahoo.com, remi_odekunle@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 15 February 2014; revised 15 March 2014; accepted 22 March 2014
Abstract
Theory has it that increasing the step length improves the accuracy of a method. In order to affirm this we increased the step length of the concept in [1] by one to get k = 5. The technique of collocation and interpolation of the power series approximate solution at some selected grid points is considered so as to generate continuous linear multistep methods with constant step sizes. Two, three and four interpolation points are considered to generate the continuous predictor-corrector methods which are implemented in block method respectively. The proposed methods when tested on some numerical examples performed more efficiently than those of [1] . Interestingly the concept of self starting [2] and that of constant order are reaffirmed in our new methods.
Keywords:Step Length, Power Series, Block Predictor, Block Corrector, Constant Order, Step Size, Grid Points, Self Starting, Efficiency

1. Introduction
In this paper we examine the solution to general second order initial value problem of the form
 (1)
(1)
In literature, it has been stated clearly the journey of the development of direct methods to offset the burden of reduction [3] -[6] . Various methods have been proposed by scholars for solving higher order ordinary differential equation (ODE). Notable authors like [1] [7] -[11] have developed direct methods of solving general second order ODE’s to cater for the burden inherent in the method of reduction. Now writing computer code is less burdensome since it no longer requires special ways to incorporate the subroutine to supply the starting values. As a result, this leads to computer time and human effort conservation.
The new methods are continuous in nature with the advantage of possible evaluation at all points within the integration interval. We have taken advantage of the works of [7] [12] -[15] who proposed direct block methods as predictor in the form
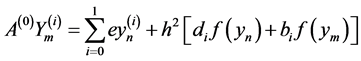 (2)
(2)
where

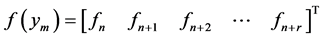
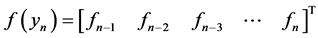
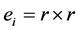 matrix,
matrix,  identity martix.
identity martix.
And also the discrete block formula as corrector in the form
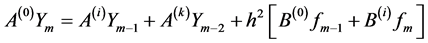 (3)
(3)
where  identity matrix
identity matrix

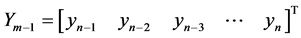
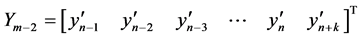
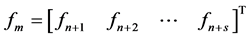
with the aim to cater for some of the setbacks of predictor-corrector method [16] [17] . The fact that interpolation point cannot exceed the order of the differential equation for block methods is worrisome [9] . Also vital to this paper is the concept of block predictor-corrector method (Milne approach). This method formed a bridge between the predictor-corrector method and block method [4] [10] [13] . In [1] we stated that results generated at an overlapping interval affect the accuracy of the method and the nature of the model cannot be determined at the selected grid points.
In this paper as in [1] , we developed a method using the Milne approach but the corrector was implemented at a non overlapping interval. The numerical experiment compared the results generated at different step lengths, when k = 4 and when k = 5 respectively.
2. Methodology
2.1. Development of the Continuous Linear Multistep Methods
We consider a power series approximate solution in the form
 (4)
(4)
where r and s are the number of interpolation and collocation points respectively.
The second derivative of (4) gives
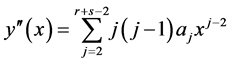 (5)
(5)
Substituting (5) into (1) gives
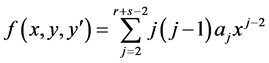 (6)
(6)
Interpolating (4) and collocating (6) at some selected grid points gives a system of non linear equations in the form
![]() (7)
(7)
where
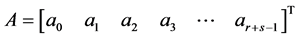
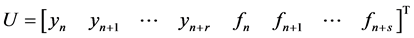

Solving (7) for the unknown constants 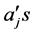 using Guassian elimination method and substituting back into (4) gives a continuous linear multistep method in the form
using Guassian elimination method and substituting back into (4) gives a continuous linear multistep method in the form
 (8)
(8)
where 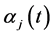 and
and 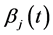 are polynomials,
are polynomials,

2.1.1. Development of the Block Predictor
Interpolating (4) at  and collocating (6) at
and collocating (6) at 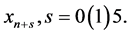 the parameters in (7) becomes
the parameters in (7) becomes
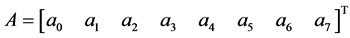

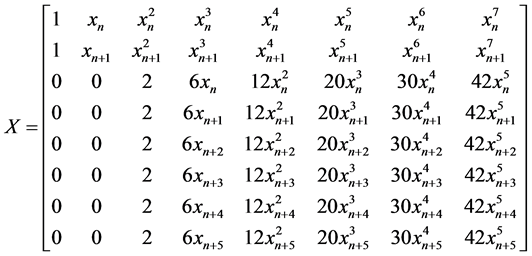
Solving for the unknown constants  using Guassian elimination method and substituting into (4), makes Equation (8) reduced to
using Guassian elimination method and substituting into (4), makes Equation (8) reduced to
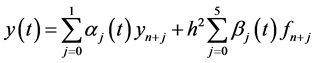 (9)
(9)
where
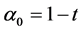
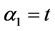
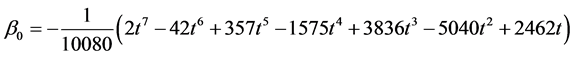
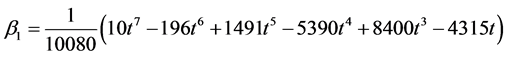
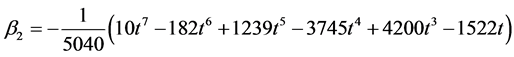
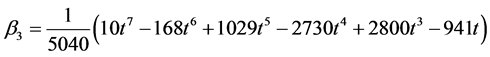
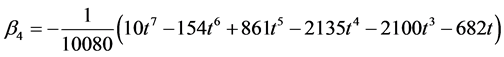
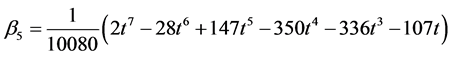
Solving for the independent solution in (9) and simplifying gives
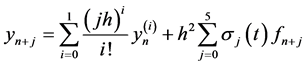 (10)
(10)
where
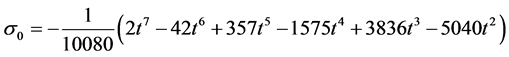
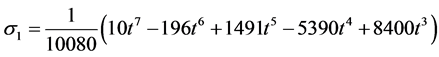
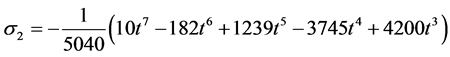
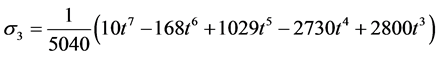
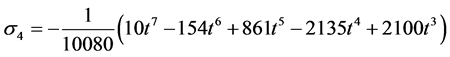
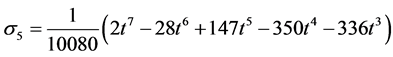
Evaluating (10) at the selected grid points, the parameters in (2) gives the following I) When ![]()
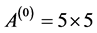 identity matrix
identity matrix
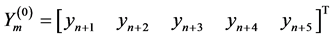
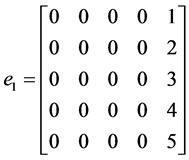
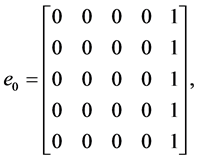
 ,
, 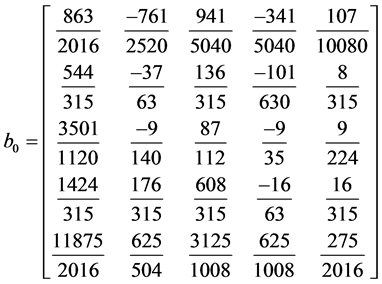
II) When ![]()

 ,
, 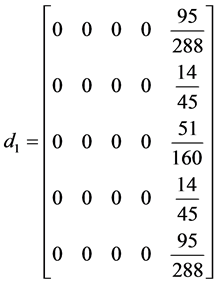
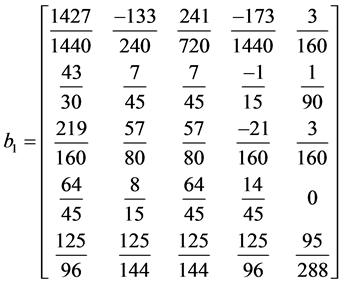
2.1.2. Development of the Block Corrector
Here there are three cases (I, II and III) to be considered.
Development of the Block Corrector for Case I
Interpolating (4) at 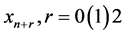 and collocating (6) at
and collocating (6) at 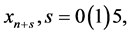 makes Equation (7) reduced to
makes Equation (7) reduced to
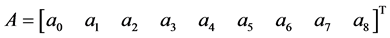

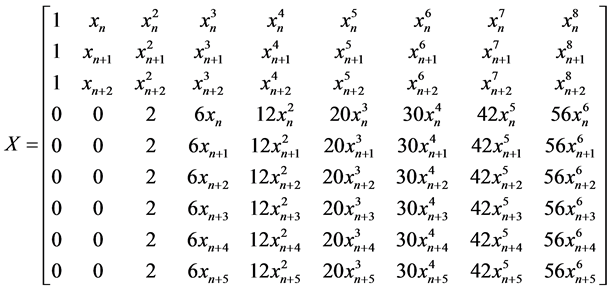
Solving for the unknown constants 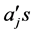 using Guassian elimination method and substituting into (4), makes Equation (8) reduced to
using Guassian elimination method and substituting into (4), makes Equation (8) reduced to
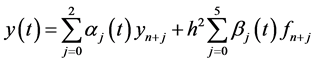 (11)
(11)
where
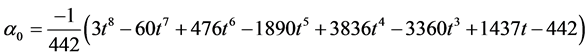
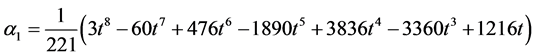
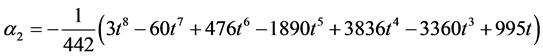
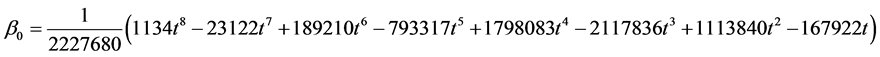

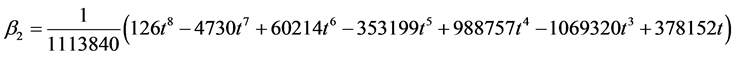
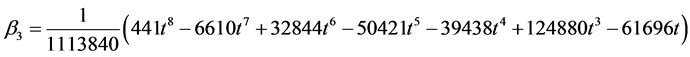
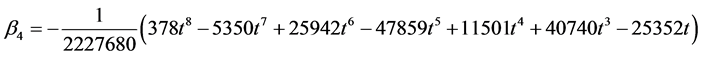
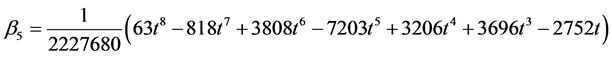
Evaluating (11) at 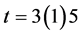 gives the following
gives the following
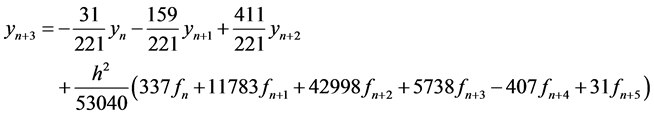 (12)
(12)
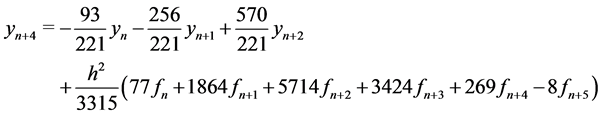 (13)
(13)
 (14)
(14)
Evaluating the first derivatives of (11) at  gives the following
gives the following
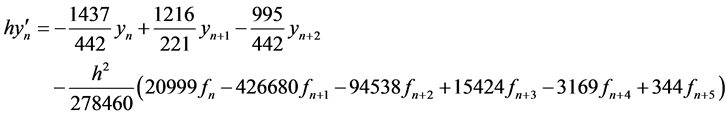 (15)
(15)
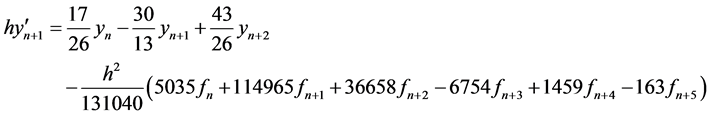 (16)
(16)
Writing Equations (12) to (16) in block form, the parameters in (3) gives the following
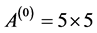 identity matrix
identity matrix
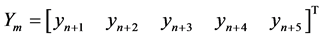
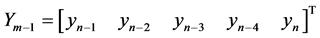
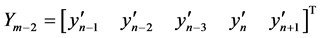
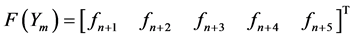
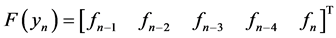
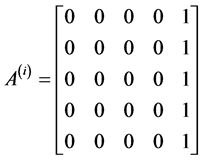 ,
, 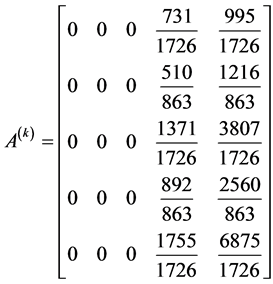
 ,
,
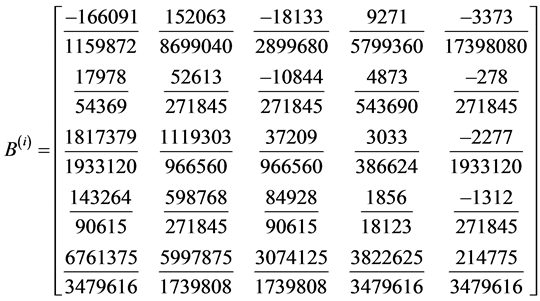
In a similar way the results for cases II and III are summarized as:
Development of the Block Corrector for Case II
 identity matrix
identity matrix

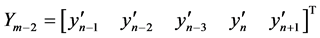
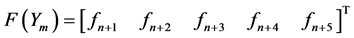
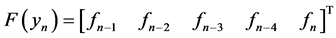
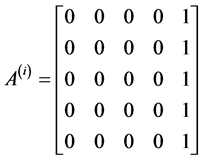 ,
, 
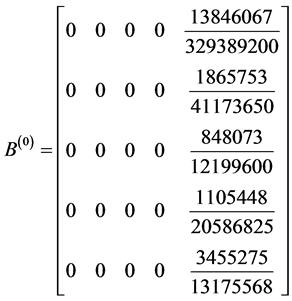
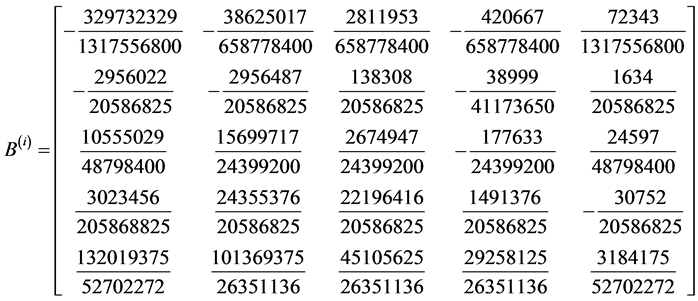
Development of Block Corrector case III
 identity matrix
identity matrix
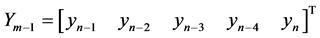
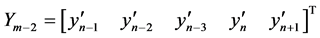
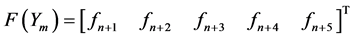

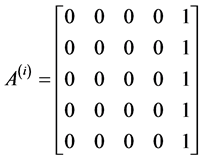 ,
, 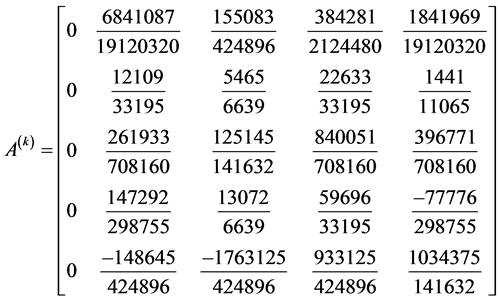
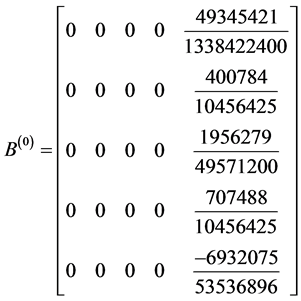
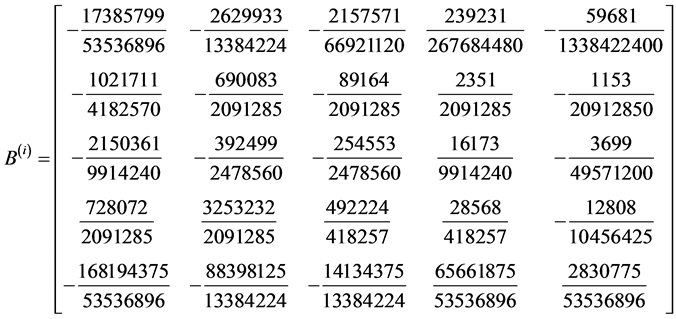
3. Analysis of the Properties of the Methods
3.1. Order of the Methods
3.1.1 Order of the Block Predictor
When 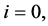 if we take a Taylor series expansion, we get
if we take a Taylor series expansion, we get
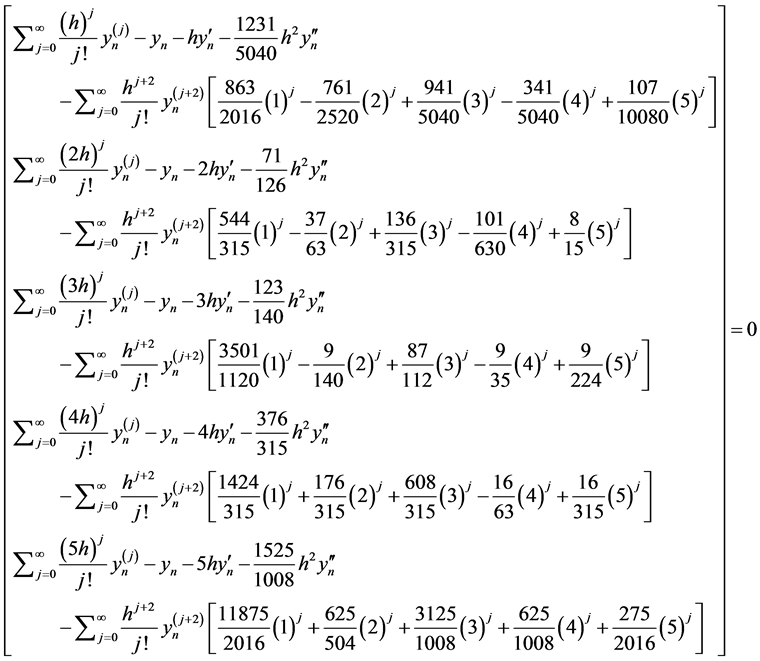
Collecting coefficients in powers of h, we see that the order of the method is six and the error constant is

Also when ![]()
The order of the method is six and the error constant is
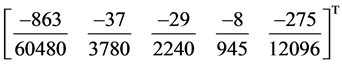
3.1.2. Order of the Block Corrector for Case I
Taking a Taylor series expansion gives
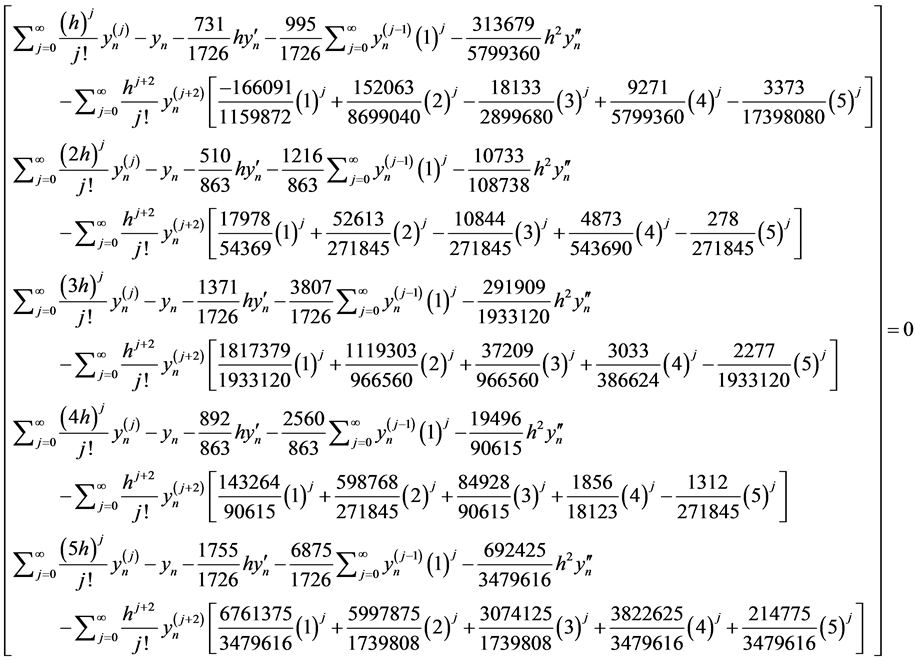
and the order of our method is seven with error constant as
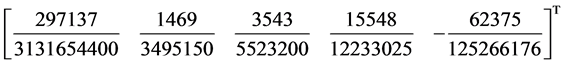
In a similar way, we compute and summarize the order for cases II and III as follows.
3.1.3. Order of the Block Corrector for Case II
In this case the order of our method is eight with error constant as
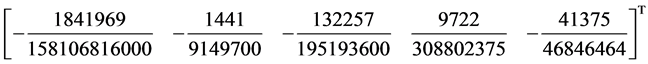
3.1.4. Order of the Block Corrector for Case III
Also using the same approach, the order of our method is nine with error constant as
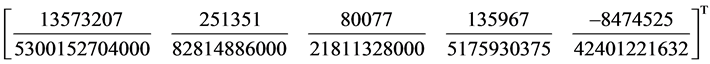
3.2. Consistency of the Method
A block method is said to be consistent if it has order 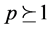 [9] .
[9] .
From the above, it clearly shows that our methods are consistent.
3.3. Zero Stability
A block method is said to be zero stable if 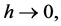 the root
the root  of the first characteristics polynomials
of the first characteristics polynomials
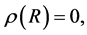 that is
that is 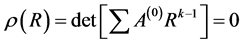 satisfying
satisfying 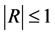 must have multiplicity equal to unity [9] .
must have multiplicity equal to unity [9] .
Applying this rule, we have that
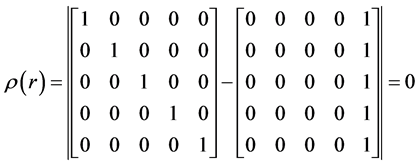
where 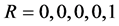 for each method. Hence the methods are zero stable
for each method. Hence the methods are zero stable
4. Numerical Experiment
4.1. Implementation
We implement the proposed methods to verify their efficacies over existing methods. To be considered are, two cases for k = 4 [1] and three cases for k = 5. Four examples were considered at h = 0.01 and h = 0.05. All computations were made with the usage of MATLAB (R2010a). An error (Err) is defined in this paper as the absolute value of the difference between the computed and expected values. The following keys are used in displaying our results on the tables for clearity.
CASE 1: Two interpolation points.
CASE II: Three interpolation points.
CASE III: Four interpolation points.
4.1.1. Test Problem I
Consider the non-linear ODE
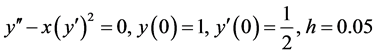
Exact Solution: 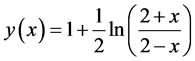
4.1.2. Test Problem 2
Consider the non-linear initial value problem
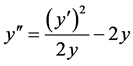 ;
; 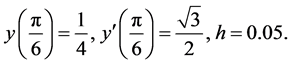
Exact solution: .
.
4.1.3. Test Problem 3
Consider the initial value ODE
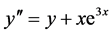 ;
; 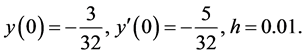
Exact solution: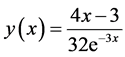 .
.
4.1.4. Test Problem 4
Consider the initial value problem
 ;
; 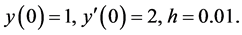
Exact solution: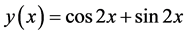 .
.
5. Discussion
We have considered two non-linear and two linear second order initial value problems in this paper as shown in Table 1 to Table 4. In [1] we compared our method with the existing methods like the block and block predictor-corrector and the results re-affirms the claim of [10] that though block predictor-corrector method takes longer time to implement, it gives better approximation than the block method. In this paper we extended the step length considered in [1] and considered varying the number of interpolation points to observe the effect on the performance of the method.
Table 1. Comparing results for different interpolation points.
Table 4. Comparing results for different interpolation points.
6. Conclusion/Recommendation
In this paper we have proposed the varying of the step length from k = 4 [1] to k = 5. Block methods which have the properties of evaluation at all points within the interval of integration are adopted to give independent solutions at non overlapping intervals as predictors to the correctors. The new method k = 5 performed better than that of k = 4. Thus it has been confirmed that varying the step length improves the accuracy of the method. However, increasing the number of interpolation points does not significantly improve the result. We therefore, recommend the block predictor-block corrector method for use in the quest for solutions to second order initial value problems of ordinary differential equations.
References
- Odekunle, M.R., Egwurube, M.O., Adesanya, A.O. and Udo, M.O. (2014) Body Math Four Steps Block PredictorBlock Corrector. Method for the Solution of
 Journal of Advances in Mathematics, 5, 746-755.
Journal of Advances in Mathematics, 5, 746-755. - Jator, S.N. and Li, J. (2009) A Self Starting Linear Multistep Method for the Direct Solution of General Second Order Initial Value Problems. International Journal of Computer Mathematics, 86, 817-836. http://dx.doi.org/10.1080/00207160701708250
- Adesanya, A.O., Odekunle, M.R. and Adeyeye, A.O. (2012) Continuous Block Hybrid-Predictor-Corrector Method for the Solution of
 International Journal of Mathematics and Soft computing, 2, 35-42.
International Journal of Mathematics and Soft computing, 2, 35-42. - Adesanya, A.O., Odekunle, M.R. and Udo, M.O. (2013) Four Steps Continuous Method for the Solution of
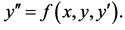 American Journal of Computational Mathematics, 3, 169-174.
American Journal of Computational Mathematics, 3, 169-174. - Awoyemi, D.O. and Kayode, S.J. (2005) A Maximal Order Collocation Method for Direct Solution of Initial Value Problems of General Second Order Ordinary Differential Equation. Proceedings of the Conference Organised by the National Mathematical Centre, Abuja.
- Jator, S.N. (2007) A Sixth Order Linear Multistep Method for Direct Solution of
 International Journal of Pure and Applied Mathematics, 40, 457-472.
International Journal of Pure and Applied Mathematics, 40, 457-472. - Awoyemi, D.O. (2001) A New Sixth Order Algorithm for General Second Order Ordinary Differential Equation. International Journal of Computer Mathematics, 77, 117-124.
- Awoyemi, D.O., Adebile, E.A., Adesanya, A.O. and Anake, T.A. (2011) Modifid Block Method for the Direct Solution of Second Order Ordinary Differential Equation. International Journal of Applied Mathematics and Computation, 3, 181-188.
- Lambert, J.D. (1973) Computational Methods in ODES. John Wiley and Sons, New York.
- Adesanya, A.O., Anake, T.A. and Udo, M.O. (2008) Improved Continuous Method for Direct Solution of General Second Order Ordinary Differential Equation. Journal of the Nigerian Association of Mathematical Physics, 13, 59-62.
- Udo, M.O., Olayi, G.A. and Ademiluyi, R.A. (2007) Linear Multistep Method for Solution of Second Order Initial Value Problems of Ordinary Differential Equations: A Truncation Error Approach. Global Journal of Mathematical Sciences, 6, 119-126.
- Zarina, B.I., Mohamed, S. and Iskanla, I.O. (2009) Direct Block Backward Differentiation Formulas for Solving Second Order Ordinary Differential Equation. Journal of Mathematics and Computation Sciences, 3, 120-122.
- James, A.A., Adesanya, A.O. and Sunday, J. (2013) Continuous Block Method for the Solution of Second Order Initial Value Problems of Ordinary Differential Equations. Journal of Mathematics and Computation Sciences, 83, 405-416.
- Awoyemi, D.O. and Idowu, M.O. (2005) A Class of Hybrid Collocation Method for Third Order Ordinary Differential Equation. International Journal of Computer Mathematics, 82, 1287-1293. http://dx.doi.org/10.1080/00207160500112902
- Awoyemi, D.O., Udo, M.O. and Adesanya, A.O. (2006) Non-Symmetric Collocation Method for Direct Solution of General Second Order Initial Value Problems of Ordinary Differential Equations. Journal of Natural and Applied Sciences, 7, 31-37.
- Awoyemi, D.O. (2003) A p-Stable Linear Multistep Method for Solving Third Order Ordinary Differential Equation. International Journal of Computer Mathematics, 80, 85-99. http://dx.doi.org/10.1080/0020716031000079572
- Yahaya, Y.A. and Badmus, A.M. (2009) A Class of Collocation Methods for General Second Order Differential Equation. African Journal of Mathematics and Computer Research, 2, 69-71.


