Applied Mathematics
Vol.5 No.4(2014), Article ID:43793,5 pages DOI:10.4236/am.2014.54069
On Classification of k-Dimension Paths in n-Cube
G. G. Ryabov, V. A. Serov
Research Computer Center of Moscow State University, Moscow State University, Moscow, Russia
Email: gen-ryabov@yandex.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 28 December 2013; revised 28 January 2014; accepted 5 February 2014
ABSTRACT
The shortest k-dimension paths (k-paths) between vertices of n-cube are considered on the basis a bijective mapping of k-faces into words over a finite alphabet. The presentation of such paths is proposed as  matrix of characters from the same alphabet. A classification of the paths is founded on numerical invariant as special partition. The partition consists of n parts, which correspond to columns of the matrix.
matrix of characters from the same alphabet. A classification of the paths is founded on numerical invariant as special partition. The partition consists of n parts, which correspond to columns of the matrix.
Keywords:n-Cube; Bijection; Cubant; k-Face; k-Path; Partition; Numerical Invariant; Hausdorff-Hamming Metrics

1. Introduction
Discovery of n-cube combinatoric properties remains a relevant topic, which extends the connections of mathematical fields [1] -[4] . The bijective mappings play an important role in enumerative combinatorics as broad alighted in classical works of G.-C. Rota and R. P. Stanley [5] [6] . Bijective form for some constructive world [7] could be considered not only as suitable for enumerative problems, but also with point of view of effective computing synthesis (algorithms and operations with the potential large parallelism) in such frame. Such approach is considered in the article on the base of constructions (computing) for k-paths as complexes of k-faces in n-cube.
2. Shortly on Cubants
One of bijections for k-faces of n-cube was proposed in [8] . Let be —reper in
—reper in , alphabet
, alphabet 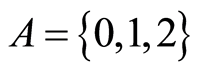 and the set
and the set  of all n-digits words. So some word of the set is
of all n-digits words. So some word of the set is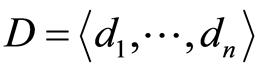 . Each k-face can be represent as Cartesian product
. Each k-face can be represent as Cartesian product  of unit-segments
of unit-segments 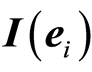 for
for 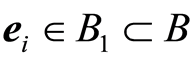 and translation
and translation 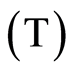 along the rest basis such, that
along the rest basis such, that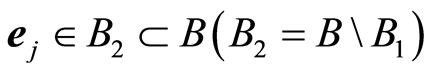 . So the bijection for k-face
. So the bijection for k-face 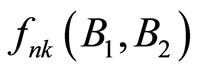 can be written as next:
can be written as next:
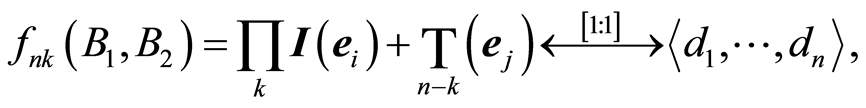
where  for
for  and
and 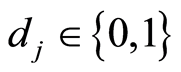 for
for .
. 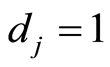 for translation along
for translation along  and
and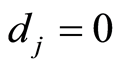 , when translation is out. Such representation allows to store traditional coding for n-cube vertex coding (vertice is 0-face). Let character
, when translation is out. Such representation allows to store traditional coding for n-cube vertex coding (vertice is 0-face). Let character  be supplement and then
be supplement and then . Character-oriented operation multiplication (intersection) is determined on
. Character-oriented operation multiplication (intersection) is determined on 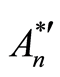 (all quaternary n-digital words) with next rules:
(all quaternary n-digital words) with next rules:

Really it’s intersection of sets: “0, 1”—endpoints of unit-segment and “2” corresponds full unit-segment. For short all words from 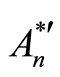 are titled as cubants. So we can say the set of cubants forms monoid with unit-cubant
are titled as cubants. So we can say the set of cubants forms monoid with unit-cubant  (n-face in n-cube, i.e. itself n-cube).
(n-face in n-cube, i.e. itself n-cube).
The character-oriented operation of addition for cubants is prescribed by next rules:
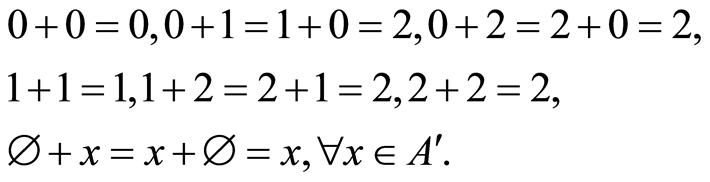
Result of the operation is cubant for convex hull face and therefore one can write:
 .
.
Short-list of operations on cubants is outlined below:
1)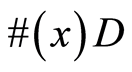 —counting of character
—counting of character 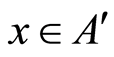 in cubant
in cubant . Result is from
. Result is from .
.
2)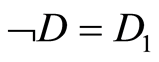 —exchanging of all “0” to “1” and all “1” to “0” in cubant
—exchanging of all “0” to “1” and all “1” to “0” in cubant . Result
. Result  is cubant for antipodal (a.p.) face.
is cubant for antipodal (a.p.) face.
3)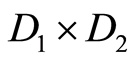 —operation multiplication. Result is cubant
—operation multiplication. Result is cubant 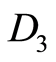 for common face, if
for common face, if . In case
. In case 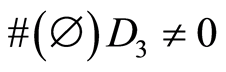 it’s
it’s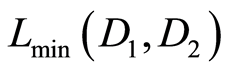 —length of shortest path along edges between faces with cubants
—length of shortest path along edges between faces with cubants  and
and , in accordance with (1).
, in accordance with (1).
4) . Result is cubant
. Result is cubant  in accordance with (2).
in accordance with (2).
5) . Exchanging letters “2” on “0” in such
. Exchanging letters “2” on “0” in such  of
of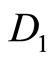 , for which
, for which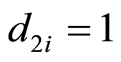 , and “2” on “1”, for which
, and “2” on “1”, for which . Result
. Result  has got properties
has got properties  and
and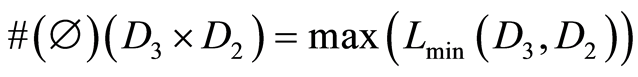 .
.
6)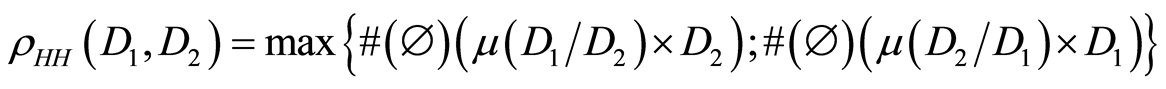 .
.
Calculation of Hausdorff-Hamming (HH) distance for faces with cubants ,
, [9] .
[9] .
7) —boundary for face with cubant
—boundary for face with cubant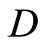 . Result is a set of cubants corresponding the all hyperfaces.
. Result is a set of cubants corresponding the all hyperfaces.
Algorithm of HH-distance calculation was proposed in [9] and all k-faces of n-cube form finite metric HH-space. Simplicity of the algorithm gives foundation to add it to operations for cubants. By the way the same algorithm realized calculation of Gromov-Hausdorff (GH) distance between cubes (as finite metric spaces) of different dimensions.
3. Matrix Representation of k-Path
Below we consider complexes of k-faces (here k-dimension of face in contrast to [4] , where k-length along edges as shortest paths between vertex). Now we will give definition of k-path between two of antipodal (a.p.) vertices in terminology of cubants. No limits of common we can consider cubants  and
and  for a.p. vertices. Then the set of cubants
for a.p. vertices. Then the set of cubants ,
,  is bijectivial form of shortest k-path such, that next conditions are satisfied for
is bijectivial form of shortest k-path such, that next conditions are satisfied for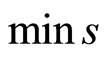 :
:
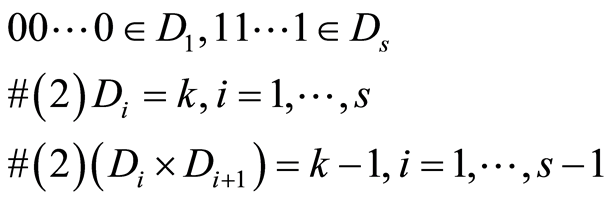
We represent set of such cubants in more visible form of 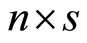 matrix
matrix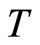 :
:

It’s easy to check next matrix corresponds to k-path for available  and
and :
:
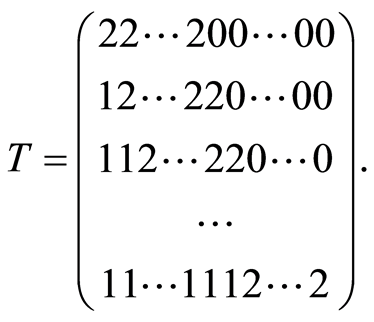
The columns of the matrix are denoted by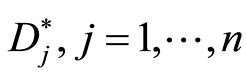 . Then available permutation of columns stores satisfying of conditions (3) and
. Then available permutation of columns stores satisfying of conditions (3) and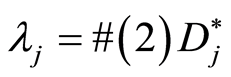 . All such matrices (under permutations from symmetric group
. All such matrices (under permutations from symmetric group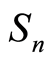 ) represent the isomorphic k-paths with partition
) represent the isomorphic k-paths with partition :
: . For case (4):
. For case (4):
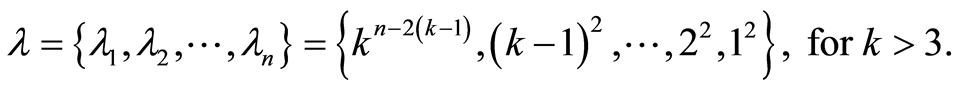 Evidently the matrices with different partitions correspond non-isomorphic k-paths. Therefore we can define the such partitions as numerical invariants, which allow one to distinguish among non-isomorphic k-paths, i.e. to classify k-paths. Now we must remark a specific property of
Evidently the matrices with different partitions correspond non-isomorphic k-paths. Therefore we can define the such partitions as numerical invariants, which allow one to distinguish among non-isomorphic k-paths, i.e. to classify k-paths. Now we must remark a specific property of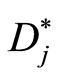 . Here the columns are written as horizontal rows. So each
. Here the columns are written as horizontal rows. So each 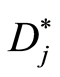 can have view only of four types:
can have view only of four types:
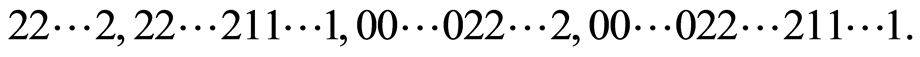
Roughly speaking the sequence of the same characters in  denies “gaps”, since otherwise the condition of
denies “gaps”, since otherwise the condition of  is not satisfied.
is not satisfied.
The specific property leads to situation, when some partitions are not represented in frame of T. For example the number of non-isomorphic k-paths classes  for
for ,
,  is equal 4, though
is equal 4, though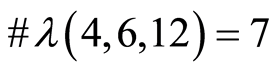 ,
,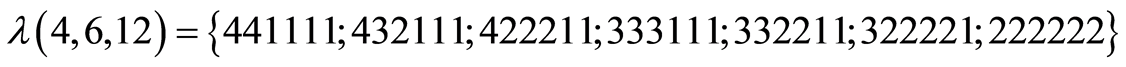 :
:
 ,
, 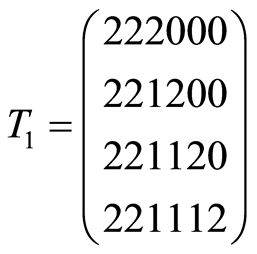 ,
, 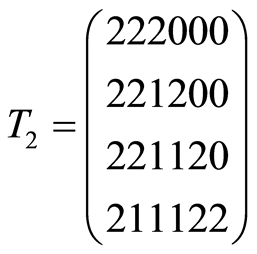 ,
, 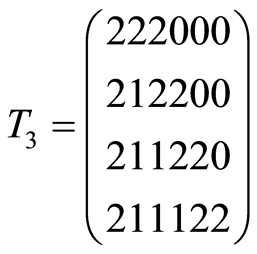 ,
, 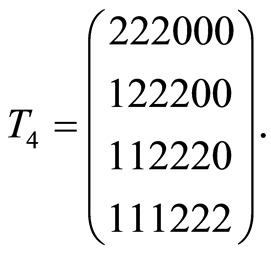
At that time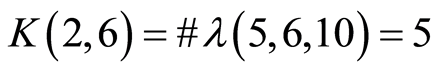 ,
,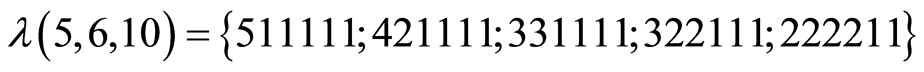 :
:
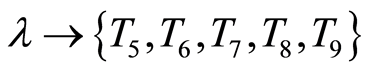 ,
, 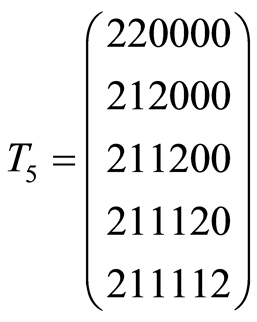 ,
, 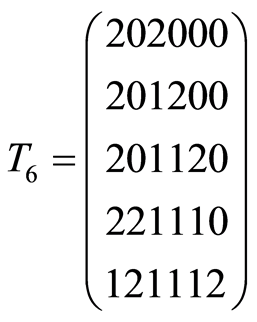 ,
, 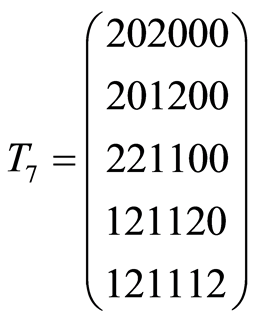 ,
, 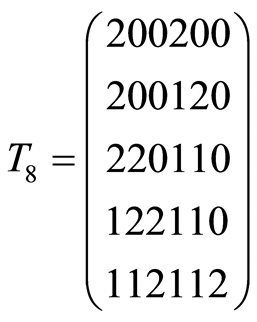 ,
, 
So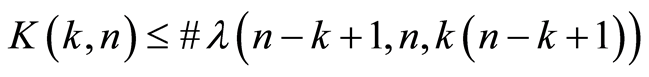 .
.
Now we consider common form of  matrix
matrix  of special type (conditions (3) are satisfied):
of special type (conditions (3) are satisfied):
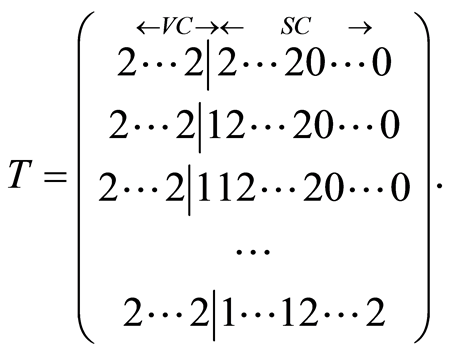
Number of vertical columns with “2” (VC) can lay in interval from 0 to 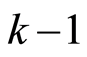 and each of them corresponds to “2-stairs” (SC) from
and each of them corresponds to “2-stairs” (SC) from  to 1, for
to 1, for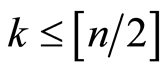 . The case
. The case  must be analyze separately. So
must be analyze separately. So  for
for  and common bounds of classes number are next:
and common bounds of classes number are next:
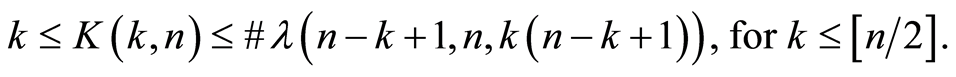
Now about case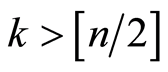 . Set SC columns includes such, which have
. Set SC columns includes such, which have 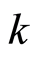 character 2, i.e. coincide with one of VC-column. The number of such SC columns is equal to
character 2, i.e. coincide with one of VC-column. The number of such SC columns is equal to . Therefore:
. Therefore:

One can combine (6) and (7) in single result:

One can give title the staircase for  of type (5).
of type (5).
We considered above k-paths for antipodal (a.p.) vertices  and
and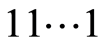 . Now let available two vertices in n-cube are given and hamming distance between them is equal to
. Now let available two vertices in n-cube are given and hamming distance between them is equal to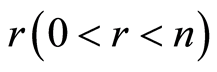 . Then computing of matrix
. Then computing of matrix  for k-path is reduced to a.p. case. Therefore we delete in pares the same
for k-path is reduced to a.p. case. Therefore we delete in pares the same 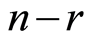 digits. So the rest
digits. So the rest  digits correspond a.p. vertices in face-convex hull for these cut vertices. Our previous techniques may be successfully here with addition of deleted
digits correspond a.p. vertices in face-convex hull for these cut vertices. Our previous techniques may be successfully here with addition of deleted 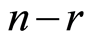 digits in columns of
digits in columns of . Shortly speaking the sequence of steps looks like this: extraction of a.p. part in given vertices (deleting of differing in pairs digits)
. Shortly speaking the sequence of steps looks like this: extraction of a.p. part in given vertices (deleting of differing in pairs digits) the choice of matrix
the choice of matrix 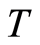 of type (5)
of type (5) inserting of columns
inserting of columns  with deleted digits in
with deleted digits in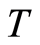 .
.
More general problem is to construct of k-path, when two a.p. vertices ,
, 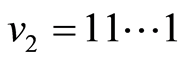 and k-face
and k-face 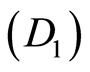 are given
are given . Without loss of generality let left digit of
. Without loss of generality let left digit of 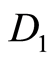 is “2”. So the first row of matrix
is “2”. So the first row of matrix  is
is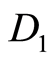 . Algorithm consists of sequential generations
. Algorithm consists of sequential generations , which follows
, which follows  in matrix
in matrix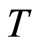 . For case
. For case  and
and 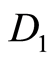 we assign
we assign  and shift character 2 in nearest digit
and shift character 2 in nearest digit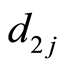 , for which
, for which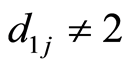 . In common case if such digit in
. In common case if such digit in  is absent, the procedure is completed. Let here
is absent, the procedure is completed. Let here  then we assign for digits
then we assign for digits  character “2” and the same characters from
character “2” and the same characters from 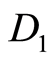 for
for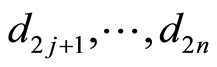 .
.
In common case for ,
,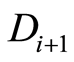 we produced in analogous fashion, beginning with duplicating in
we produced in analogous fashion, beginning with duplicating in 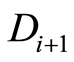 the same characters of
the same characters of  before first meeting “2”. Then we assign “1” for next digit of
before first meeting “2”. Then we assign “1” for next digit of 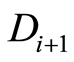 and further digits are determined in accordance with rules for
and further digits are determined in accordance with rules for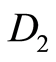 . One can represent the digit-wise rules as next scheme:
. One can represent the digit-wise rules as next scheme:
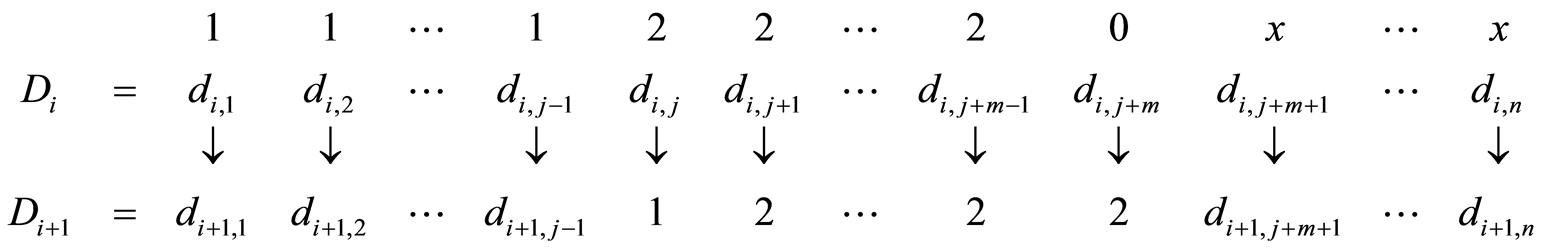
One can give title of the procedure as pressing characters “2” with single inversion 0 - 1.
Examples of 2-paths in 6-cube is represented step by step below (Figure 1).
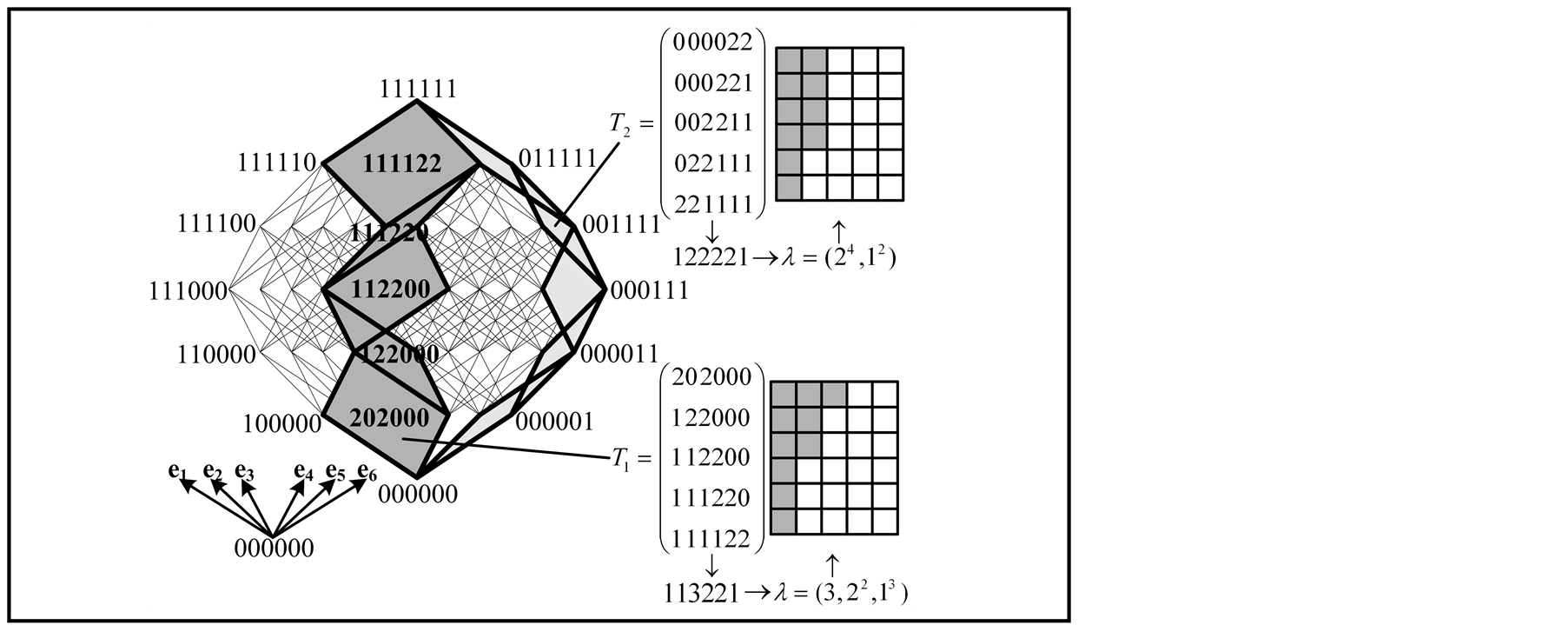
Figure 1. 2-paths (T1, T2) are drawn onto flat projection of 2-skeletone of 6-cube.
HH-distance may be taken in account constructing some k-paths (operation 6)). So 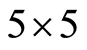 table
table 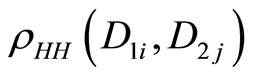 for
for  and
and  (2-paths in 6-cube) is following:
(2-paths in 6-cube) is following:
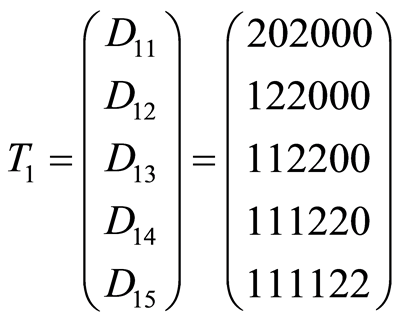 ,
, 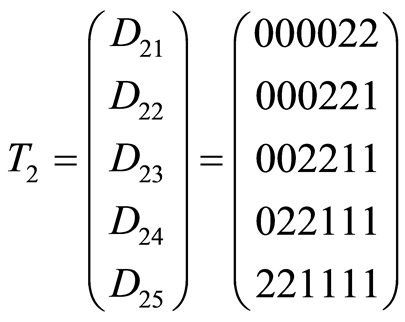 ,
, 
It follows: 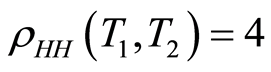 (Figure 1).
(Figure 1).
To remark although our exposition is short, the most of operations for cubants are realized digitwise, i.e. in parallel. It’s clearly visible, if we’ll use for computer the bitwise mapping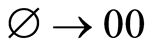 ,
, 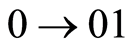 ,
, 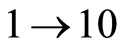 ,
,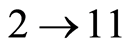 .
.
4. Conclusions
In conclusion, we give the main statement of the article.
Minimal number s of k-faces in k-path between a.p. vertices in n-cube is equal to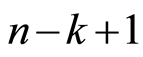 . The bounds for number of non-isomorphic k-path classes are
. The bounds for number of non-isomorphic k-path classes are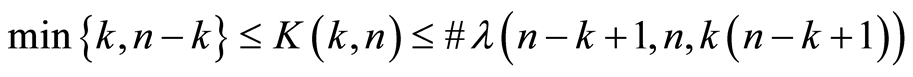 , where
, where  are partitions integer
are partitions integer  in
in 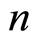 parts with constraint
parts with constraint  for maximal part. Lower bound
for maximal part. Lower bound 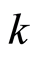 is always realized by staircase matrix.
is always realized by staircase matrix.
References
- Mollard, M. and Ramras, M. (2013) Edge Decompositions of Hypercubes by Paths and by Cycles. http://arxiv.org/pdf/1205.4161.pdf
- Mundici, D. (2012) Logic on the n-Cube. http://arxiv.org/pdf/1207.5717.pdf
- Leader, I. and Long, E. (2013) Long Geodesics in Subgraphs of the Cube. http://arxiv.org/pdf/1301.2195.pdf
- Erde, J. (2013) Decomposing the Cube into Paths. http://xxx.tau.ac.il/pdf/1310.6776.pdf
- Rota, G.-C. and Metropolis, N. (1978) Combinatorial Structure of the Faces of the n-Cube. SIAM Journal on Applied Mathematics, 35, 689-694. http://dx.doi.org/10.1137/0135057
- Stanley, R.P. (1999) Enumerative Combinatorics. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511609589
- Manin, Y.I. (1999) Classical Computing, Quantum Computing, and Shor’s Factoring Algorithm. http://arxiv.org/pdf/quant-ph/9903008.pdf
- Ryabov, G.G. (2009) On the Quaternary Coding of Cubic Structures. (in Russian) http://num-meth.srcc.msu.ru/zhurnal/tom_2009/pdf/v10r138.pdf
- Ryabov, G.G. (2011) Hausdorff Metric on Faces of the n-Cube. Journal of Mathematical Sciences, 177, 619-622. http://dx.doi.org/10.1007/s10958-011-0487-3

