Applied Mathematics
Vol.5 No.1(2014), Article ID:41822,9 pages DOI:10.4236/am.2014.51015
On the Rotation of a Vector Field in a Four-Dimensional Space
UniFOA—Centro Universitário de Volta Redonda, Volta Redonda, Brazil
Email: simal.leonardo@terra.com.br, leonardo.moreira@foa.org.br
Received November 5, 2013; revised December 5, 2013; accepted December 12, 2013
ABSTRACT
Recently I published a paper in the journal ALAMT (Advances in Linear Algebra & Matrix Theory) and explored the possibility of obtaining products of vectors in dimensions higher than three [1]. In continuation to this work, it is proposed to develop, through dimensional analogy, a vector field with notation and properties analogous to the curl, in this case applied to the space IR4. One can see how the similarities are obvious in relation to the algebraic properties and the geometric structures, if the rotations are compared in spaces of three and four dimensions.
Keywords:Products of Vectors; Dimensional Analogy; Vector Fields; Curl; Rotations; Curl by Analogy
1. Introduction
[1] has defined a similar operation to the cross product, to a space of dimension n. In particular, for a 4-dimensional Cartesian space with Euclidean norm, we have the following results:
Given three linearly independent vectors, 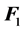 ,
, 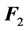 and
and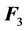 , such that
, such that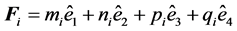 , then:
, then:
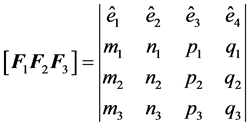 , (1)
, (1)
being
 . (2)
. (2)
The relationship between the norms of the vectors 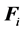 is given by:
is given by:
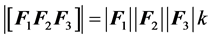 , (3)
, (3)
where
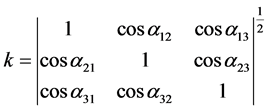 . (4)
. (4)
In (4), 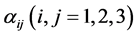 represents the angles between two vectors that generate the product
represents the angles between two vectors that generate the product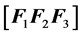 , with conditions established in [1].
, with conditions established in [1].
2. Basic Properties of Vector Operators in Four Dimensions
Be summarized important properties about vector operators, here extended to four dimensions, with the objective of situate the reader on what is intended to present in Section 3. In these results, it is considered that
 and
and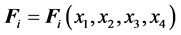 ,
, 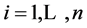 , respectively represent scalar fields and vector fields on IR4, with defined partial derivatives.
, respectively represent scalar fields and vector fields on IR4, with defined partial derivatives.
2.1. The Del Operator in Four Dimensions
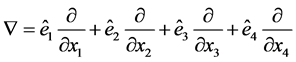 , (5)
, (5)
being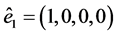 ,
, 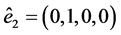 ,
, 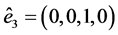 and
and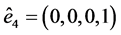 .
.
2.2. The Gradient in Four Dimensions
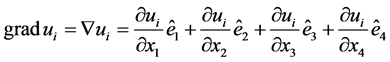 . (6)
. (6)
It is valid the following elementary property:
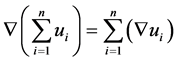 (P1)
(P1)
2.3. The Divergence in Four Dimensions
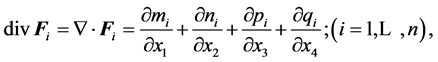 (7)
(7)
considering that , and further
, and further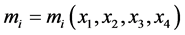 ,
, 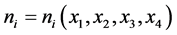 ,
, 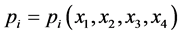 and
and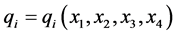 .
.
It is valid the following elementary property:
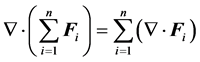 (P2)
(P2)
2.4. Relationship between the Gradient and the Divergence
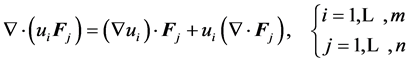 (P3)
(P3)
2.5. The Laplacian in Four Dimensions
2.5.1. The Laplacian of ui
 (8)
(8)
2.5.2. The Laplacian of Fi
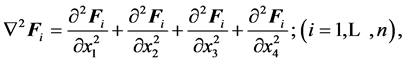 (9)
(9)
3. Curl by Analogy in IR4
It is proposed to introduce an analog curl in IR4. Given two vector fields in IR4, represented by and
and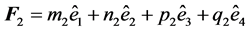 , consider the vector product
, consider the vector product
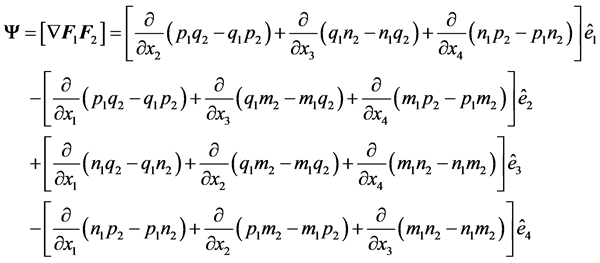 (10)
(10)
It is important to note that this definition provides for the inclusion of two vector fields simultaneously in the calculations.
In the remainder of this paper, the vector field 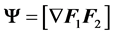 is identified by the symbol
is identified by the symbol , where
, where 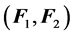 is related to the ordered nature of the product of vector, and
is related to the ordered nature of the product of vector, and 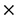 characterizes its vectorial aspect (however, it should be noted that there is no relation with the usual cross product, defined in IR3).
characterizes its vectorial aspect (however, it should be noted that there is no relation with the usual cross product, defined in IR3).
In compact notation, 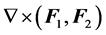 may be represented by the symbolic determinant
may be represented by the symbolic determinant
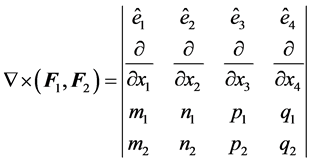 . (11)
. (11)
The analogy with the curl is based on a symbolic notation, obtained based on structure of determinants and their relationship with the vector “Del”. In subsequent section will be shown how this vector thus defined is associated to the rotational motion in four-dimensional space.
Rotational motion, here and in the remainder of this paper, should not be interpreted as a movement with real physical meaning, but only in the context of geometric relations between vectors.
4. Properties of the Vector 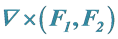
Adding to the basic properties (P1)-(P3) involving , which are valid in any dimension, presents the following properties associated with the vector
, which are valid in any dimension, presents the following properties associated with the vector  and valid in space IR4:
and valid in space IR4:
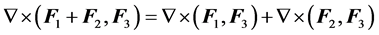 (P4)
(P4)
Corollary:
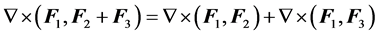 (C-4.1)
(C-4.1)
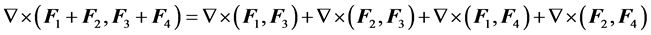 (C-4.2)
(C-4.2)
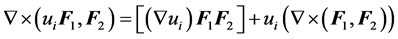 (P5)
(P5)
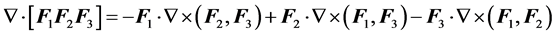 (P6)
(P6)
 (P7)
(P7)
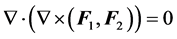 (P8)
(P8)
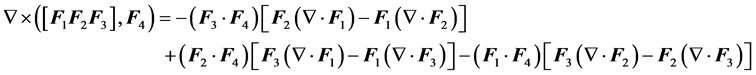 (P9)
(P9)
 (P10)
(P10)
All vector functions present in these properties are such as in formulas (5) to (9). It properties as above has a clear parallel with the formulas involving the curl presented in [2]. Demonstrations (P4) to (P8) are elementary, simply by the development of both members of the equations. To check the properties (P9) and (P10), one must show first the following identity relating five vectors in space IR4:
PROPOSITION Given the vectors A, B, C, D, E, then:
 (12)
(12)
PROOF: If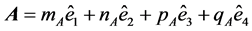 ,
, 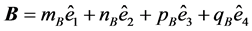 ,
, 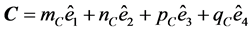 ,
, 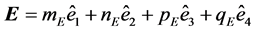
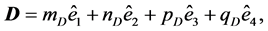 , then:
, then:
(a)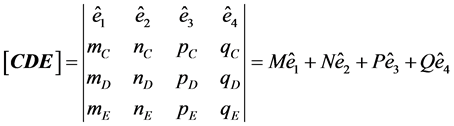 being
being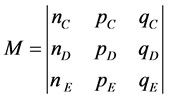 ,
, 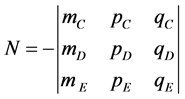 ,
, 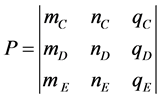 and
and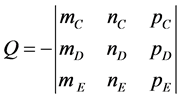 , developed according to the definition (1);
, developed according to the definition (1);
(b)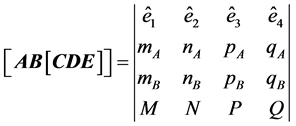 ;
;
Substituting (a) in (b), developing and arranging the terms conveniently:
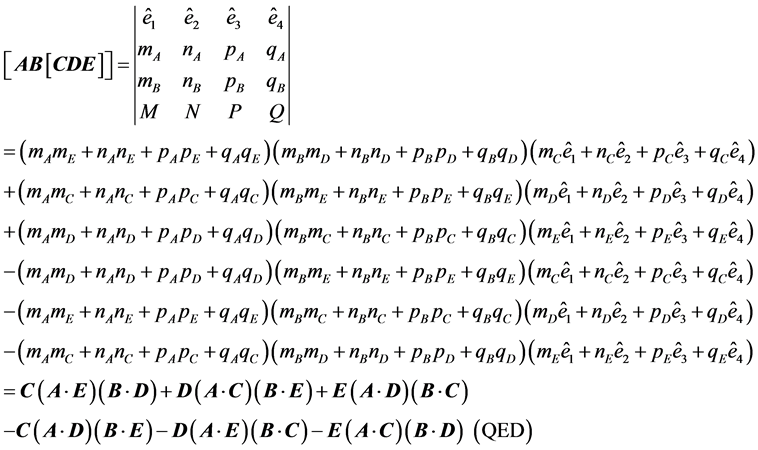
From (12), and considering the product of vectors written in the order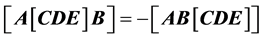 :
:
By making the identifications , one obtains immediately the formula (P9);
, one obtains immediately the formula (P9);
By making the identifications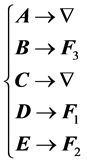 , one obtains immediately the formula (P10).
, one obtains immediately the formula (P10).
5. Geometric Interpretations for Vector Ψ
For convenience of notation, we identify the four spatial coordinates in IR4 by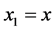 ,
, 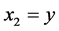 ,
,  and
and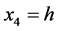 .
.
5.1. The Angular Velocity
Consider, in IR³, the velocity 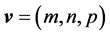 applied to a point P in space, determined by the position vector
applied to a point P in space, determined by the position vector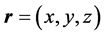 , so that the point P perform a plan rotational motion with constant frequency. The angular velocity of this rotational motion is
, so that the point P perform a plan rotational motion with constant frequency. The angular velocity of this rotational motion is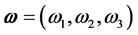 .
.
Since the three vectors are related in the equation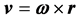 , is simple to demonstrate the well-known relation
, is simple to demonstrate the well-known relation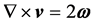 , in other words, the curl of velocity
, in other words, the curl of velocity 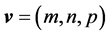 is a vector collinear to the vector
is a vector collinear to the vector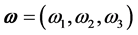 , and twice the norm.
, and twice the norm.
The idea geometric of rotation will be extended to a space of four dimensions. Consider, therefore, the vector 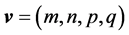 applied to a point P of the four-dimensional space, determined by the vector
applied to a point P of the four-dimensional space, determined by the vector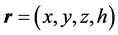 , so that the point P also perform a a plan rotational motion with constant frequency. The angular velocity of this rotational motion is
, so that the point P also perform a a plan rotational motion with constant frequency. The angular velocity of this rotational motion is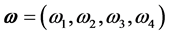 .
.
The objective is to define a geometrical framework that relates the vectors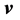 ,
, 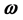 and
and  for the IR4, which is analogous to existing framework in IR3. The concept of rotation is presented here in a narrow sense. For a broader approach is recommended to consult [3,4].
for the IR4, which is analogous to existing framework in IR3. The concept of rotation is presented here in a narrow sense. For a broader approach is recommended to consult [3,4].
According to [1], to obtain the vector 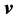 from the vectors
from the vectors 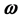 and
and 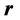 in IR4, it is necessary to have a fourth vector. Given the nature of rotation as circular with constant frequency, the vectors
in IR4, it is necessary to have a fourth vector. Given the nature of rotation as circular with constant frequency, the vectors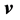 ,
, 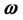 and
and 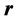 are two by two perpendicular.
are two by two perpendicular.
Let us introduce a vector 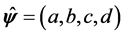 having the following properties:
having the following properties:
A) 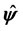 is perpendicular simultaneously to the three vectors
is perpendicular simultaneously to the three vectors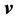 ,
, 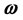 and
and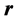 ;
;
B)  is a unit vector;
is a unit vector;
C) 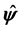 is a dimensionless vector.
is a dimensionless vector.
These restrictions are intended:
1) Simplify the proportionality constant that relates the norms of the vectors involved in the product. In this case, by (4),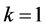 .
.
2) Do not change the relationship ;
;
3) Make the equation of the previous item remains dimensionally consistent.
The components of the vector 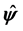 are obtained from the solution of the system (e1)-(e4), modeled on the arguments presented above:
are obtained from the solution of the system (e1)-(e4), modeled on the arguments presented above:
(e1) 
(e2) 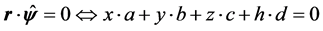
(e3) 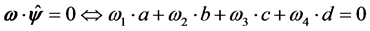
(e4) 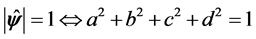
The solution to this system of equations is given by:
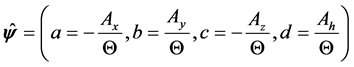 , (13)
, (13)
where:
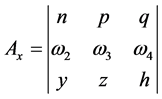 , (14)
, (14)
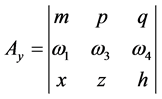 , (15)
, (15)
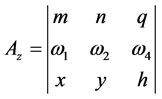 , (16)
, (16)
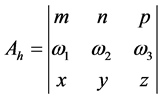 , (17)
, (17)
 . (18)
. (18)
Thus, the vector  can be noted more compactly:
can be noted more compactly:
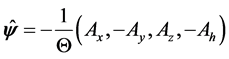 , (19)
, (19)
or
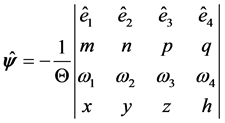 , (20)
, (20)
or more simply:
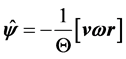 . (21)
. (21)
It is interesting to note that the vector 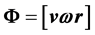 has the dimensions
has the dimensions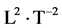 .
.
With these definitions and results, the vector  is obtained from the equation:
is obtained from the equation:
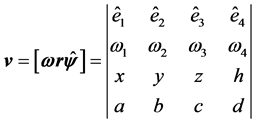 , (22)
, (22)
and the components of the vector v are given by:
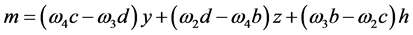 , (23)
, (23)
 , (24)
, (24)
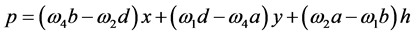 , (25)
, (25)
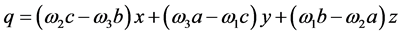 . (26)
. (26)
The components  of v are determined simultaneously with the components
of v are determined simultaneously with the components 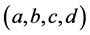 of
of .
.
Note also that:
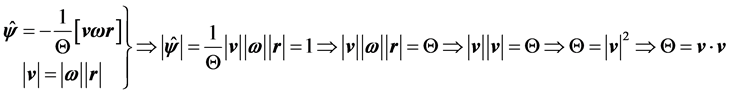
that is,
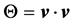 . (27)
. (27)
5.2. Relationship between the Vectors ω and 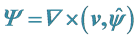
Consider the analogous to the curl vector, given by
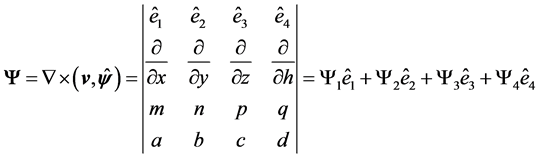 (28)
(28)
By using relations (23)-(26), shows that:
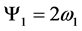 ,
, 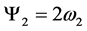 ,
, 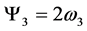 ,
,  , so that
, so that
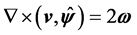 . (29)
. (29)
This result shows that the relationship between curl and angular velocity remains the same, when using the vector analogous to the curl, in four-dimensional space. The dimensions of the vectors are also consistent, namely, both have dimensions .
.
It should be noted that there is no intention to give physical meaning to these equations. Even the dimensional analysis is being treated here purely mathematical levels.
The following shows that the vector  in IR4 is reduced in the known cases in IR3.
in IR4 is reduced in the known cases in IR3.
5.3. Particular Cases
5.3.1. Projection onto IR3
a) Usual cross product and curl Being ,
, 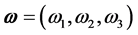 and
and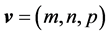 , are well known the results:
, are well known the results:
 (a.1)
(a.1)
 (a.2)
(a.2)
b) Curl by analogy If we consider the vectors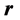 ,
, 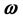 and
and 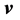 like projections from the space IR4 onto space IR3, concordant results are obtained as follows:
like projections from the space IR4 onto space IR3, concordant results are obtained as follows:
Consider 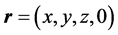
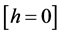 ,
, 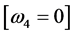
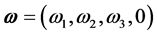 and
and 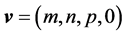
 .
.
It is calculated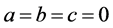 ,
, 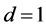 , and from the relations (23)-(26) we arrive at
, and from the relations (23)-(26) we arrive at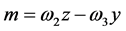 ,
, 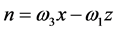 ,
,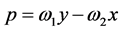 . Therefore:
. Therefore:
 (b.1)
(b.1)
5.3.2. Projection onto IR2
c) Usual cross product and curl Being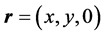 ,
,  and
and , are well known the results:
, are well known the results:
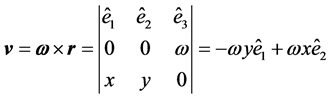 (c.1)
(c.1)
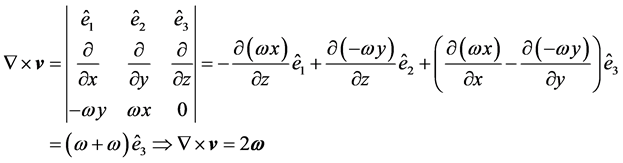 (c.2)
(c.2)
d) Curl by analogy If we consider the vectors r,  and
and  like projections from the space IR4 onto space IR2, concordant results are obtained as follows:
like projections from the space IR4 onto space IR2, concordant results are obtained as follows:
Consider 
 ,
, 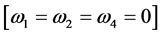
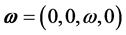 and
and 
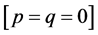 .
.
It is calculated ,
, 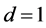 , and from the relations (23)-(26) we arrive at
, and from the relations (23)-(26) we arrive at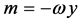 ,
, . Therefore:
. Therefore:
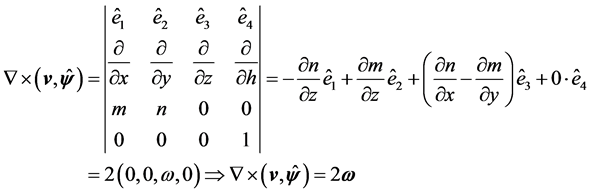 (d.1)
(d.1)
6. Conclusions
Through dimensional analogies and structures based on determinants, we could get a vector field in a space of four dimensions, with algebraic and geometric properties, equivalent to the properties of vector curl commonly defined in IR3.
Subsequent developments show that the “curl by analogy” thus obtained reduces to the three-dimensional case when the fourth coordinate is null in their constitutive equations.
The geometric frameworks that relate to the vectors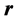 ,
, 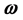 and
and  in a circular rotational motion with constant frequency are equivalent in three and four dimensions, and the appendix of this work also suggests that they are equivalent in any dimension. Discussing the behavior of the vector
in a circular rotational motion with constant frequency are equivalent in three and four dimensions, and the appendix of this work also suggests that they are equivalent in any dimension. Discussing the behavior of the vector 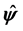 during such rotations will be the subject of future analysis.
during such rotations will be the subject of future analysis.
This paper is not intended, of course, to give any physical interpretation of the quantities involved, but only to demonstrate the algebraic and geometric analogies related to the rotation in three and four dimensions, including the demonstration of consistency with regard to dimensional analysis.
In future work it is intended to apply the results obtained in triads of vectors with similar relationships to those in between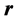 ,
, 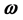 and
and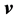 , such as, for example, in relation
, such as, for example, in relation 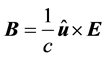 between the magnetic induction B, electric field E, and vector directional of propagation of electromagnetic wave, represented by
between the magnetic induction B, electric field E, and vector directional of propagation of electromagnetic wave, represented by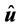 .
.
REFERENCES
- L. Simal Moreira, “Geometric Analogy and Products of Vectors in n Dimensions,” Advances in Linear Algebra & Matrix Theory, Vol. 3, No. 1, 2013, pp. 1-6. http://dx.doi.org/10.4236/alamt.2013.31001
- M. R. Spiegel, S. Lipschutz and J. Liu, “Mathematical Handbook of Formulas and Tables,” 3rd Edition, Schaum’s Outline Series, McGraw-Hill New York, 2009.
- F. N. Cole, “On Rotations in Space of Four Dimensions,” American Journal of Mathematics, Vol. 12, No. 2, 1890, pp. 191-210. http://www.jstor.org/stable2369715
- H. P. Manning, “Geometry of Four Dimensions,” Dover Publications Mineola, 1956.
Appendix
There is no difficulty in extending the ideas about rotations presented in this work to higher dimensions, simply just utilize the aforementioned systematic increase of coordinates for points and vectors, as well as rows and columns to the determinants that make up the structures generating products of vectors [1]. Indeed, for any dimension n would:
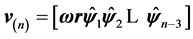 , (A1)
, (A1)
or
 . (A2)
. (A2)
And also:
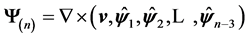 , (A3)
, (A3)
or
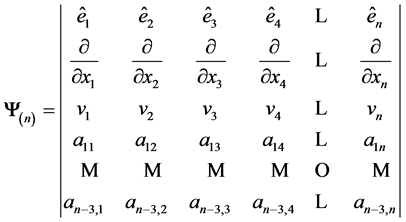 . (A4)
. (A4)

