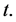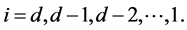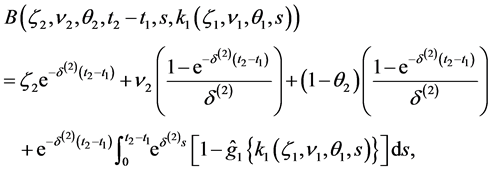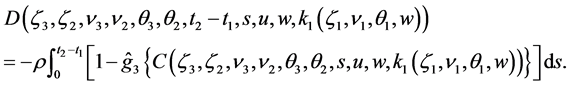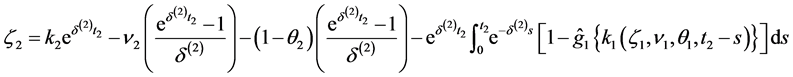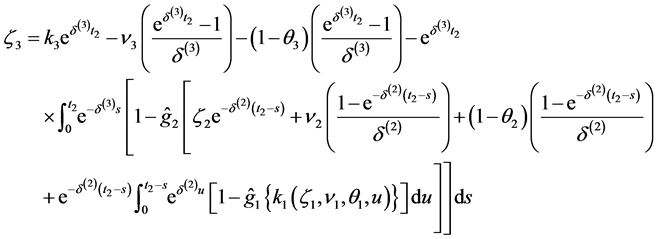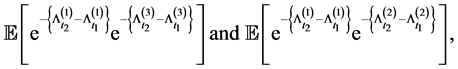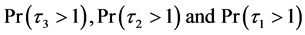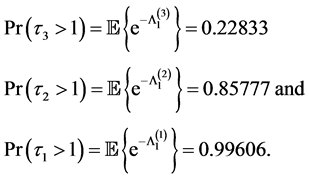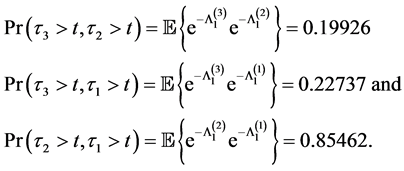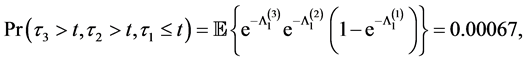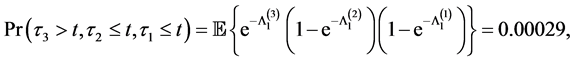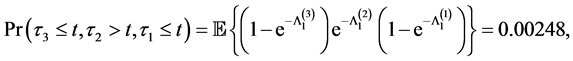Applied Mathematics
Vol.05 No.03(2014), Article ID:42796,12 pages
10.4236/am.2014.53047
The Distribution of Multiple Shot Noise Process and Its Integral
Jiwook Jang
Department of Applied Finance & Actuarial Studies, Faculty of Business and Economics, Macquarie University, Sydney, Australia
Email: jiwook.jang@mq.edu.au
Copyright © 2014 Jiwook Jang. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Jiwook Jang. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received October 30, 2013; revised November 30, 2013; accepted December 7, 2013
ABSTRACT
In this paper, we study multiple shot noise process and its integral. We analyse these two processes systematically for their theoretical distributions, based on the piecewise deterministic Markov process theory developed by Davis [1] and the martingale methodology used by Dassios and Jang [2]. The analytic expressions of the Laplace transforms of these two processes are presented. We also obtain the multivariate probability generating function for the number of jumps, for which we use a multivariate Cox process. To derive these, we assume that the Cox processes jumps, intensity jumps and primary event jumps are independent of each other. Using the Laplace transform of the integral of multiple shot noise process, we obtain the tail of multivariate distributions of the first jump times of the Cox processes, i.e. the multivariate survival functions. Their numerical calculations and other relevant joint distributions’ numerical values are also presented.
Keywords:
Multiple Shot Noise Process and Its Integral; Multivariate Cox Process; Piecewise Deterministic Markov Process; Martingale Methodology; Multivariate Survival Functions
1. Introduction
Due to global warming and climate changes, there have been increases in the frequency and intensity of floods in one area and draught in the other. So administrating the level of water in dams and rivers becomes much more significant task than ever before. Single (Poisson) shot noise process can be used to model the level of water in dams and rivers, but it is quite inadequate as rains do not occur according to only a Poisson process [3].
Increases in the frequency and intensity of storms, hail, bushfires and earthquakes have revealed shortcomings in the ways Catastrophe Insurance is priced. Hence more complicated models are needed to accommodate increasing frequency and intensity of catastrophic events. A Cox process with shot noise intensity has been suggested to use to predict claims arising from catastrophic events by Dassios and Jang [2].
In financial industry, a shock which initially affects a couple of institutions or a particular region of the economy spreads to the rest of the financial industry and then infects the larger economy. This is called “financial contagion” [4,5]. The US federal takeover of Fannie Mae and Freddie Mac, the Bank of America takeover of Countrywide Financial Corporation and the bankruptcy of New Century Financial Corporation due to mismanagement of subprime mortgage in US are the examples of financial contagion. The prevalence of above financial contagion has led to further bankruptcies and default of mortgage lenders in US announcing their significant losses in 2008. This subprime mortgage meltdown has also led to new ownership for Bears Stern and Merrill Lynch and the bankruptcy of Lehman Brothers. These contagious events have caused the collapse of stock prices in worldwide and it has shaken global financial markets further due to new waves of default and bankruptcy. Due to the failing of financial institutions in 2008, systemic risk has become the main concern to the governments requiring their interventions to ameliorate these contagious effects to the larger economy [6].
To these effects, in this paper we introduce multiple shot noise process [7]. It consists of  component
component
processes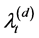 ,
, 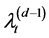 ,
,  ,
, 
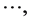 where each process acts as a jump intensity for the next one. For
where each process acts as a jump intensity for the next one. For
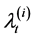
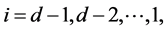 decays with rate
decays with rate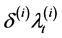 , and additive jumps occur with rate of
, and additive jumps occur with rate of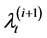 , i.e. each
, i.e. each
process acts as a jump intensity for the next one. Jump sizes are independent but not identically distributed
random variables with distribution function 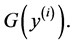
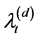 decays with rate
decays with rate 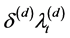 but its jump arrival rate
but its jump arrival rate
is deterministic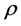 . Its jump sizes have distribution function
. Its jump sizes have distribution function 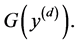 Hence multiple shot noise process we consider has the following structure:
Hence multiple shot noise process we consider has the following structure:
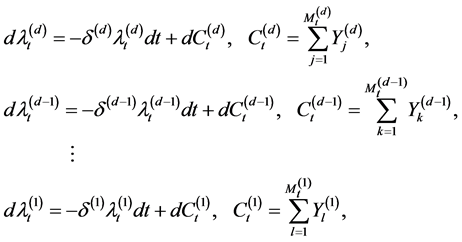 (1)
(1)
where:
・ 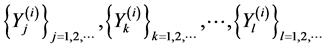 are sequences of independent but not identically distributed random
are sequences of independent but not identically distributed random
variables with distribution function 
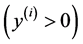 and
and 
・ 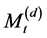
・ 
We also make the additional assumption that the point process 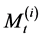

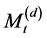

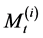
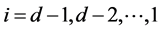
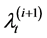

The process 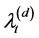 is triggered by jumps (or primary events, or shocks) that will result in a positive jump in the process. As time passes, the process decreases with rate
is triggered by jumps (or primary events, or shocks) that will result in a positive jump in the process. As time passes, the process decreases with rate  until another jump (or event) occurs which again will result in a positive jump in the process. The process
until another jump (or event) occurs which again will result in a positive jump in the process. The process 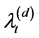 is the jump arrival rate for the
is the jump arrival rate for the 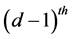 process
process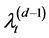 , and the process
, and the process 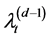 is the jump arrival rate for the
is the jump arrival rate for the 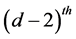 process
process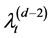 , and so on. Hence the process
, and so on. Hence the process  is the prime trigger in influencing all other relative processes. As time passes, the processes
is the prime trigger in influencing all other relative processes. As time passes, the processes 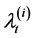 decrease with rate
decrease with rate  for
for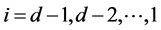 , and additive jumps occur.
, and additive jumps occur.
We use another Cox process 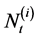 for
for 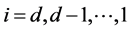 to model the multivariate jump time and derive the tail of multivariate distribution of the first jump times of the Cox processes, i.e. the multivariate survival function, where it is assumed that the jumps in
to model the multivariate jump time and derive the tail of multivariate distribution of the first jump times of the Cox processes, i.e. the multivariate survival function, where it is assumed that the jumps in 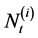 for
for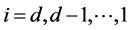 , the jumps in
, the jumps in 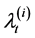 for
for  and primary event jumps in
and primary event jumps in 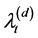 are independent of each other.
are independent of each other.
If 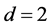 (i.e.
(i.e. ), this process becomes a double shot noise process, and it can be considered to model the level of water in dams and rivers using this process. Applying a double shot noise process in insurance context can be noticed in Dassios and Jang [11].
), this process becomes a double shot noise process, and it can be considered to model the level of water in dams and rivers using this process. Applying a double shot noise process in insurance context can be noticed in Dassios and Jang [11].
In Section 2, we start with deriving the Laplace transform of the vector
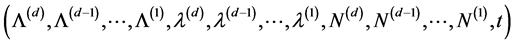
using the martingale methodology in Dassios and Jang [2], with which we obtain the expression for
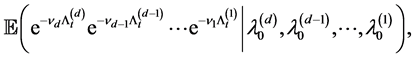 (1.2)
(1.2)
where  and
and  for
for  For simplicity, it is assumed that
For simplicity, it is assumed that 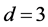 but it
but it
can be easily extended to the higher dimensions. Using (1.2) in Section 3, we derive the tail of the multivariate
distribution of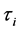 ’s, where
’s, where , i.e.
, i.e.
 (1.3)
(1.3)
that is equivalent to the first jump time of the Cox process . The expressions for relevant multivariate distributions such as
. The expressions for relevant multivariate distributions such as
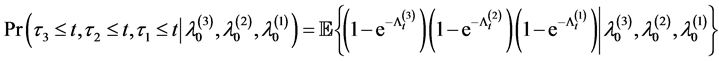 (1.4)
(1.4)
and
 (1.5)
(1.5)
are omitted as they can easily be obtained using (1.2) and (1.3), but their numerical calculations are shown in Section 4. Section 5 contains some concluding remarks.
2. The Laplace Transform of the Vector 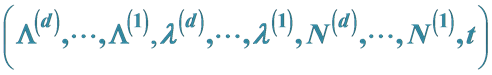
We firstly consider using the Laplace transform of the vector

to derive the tail of the multivariate distribution of ’s. Once its expression is obtained, we can easily derive the tail of the multivariate distribution of
’s. Once its expression is obtained, we can easily derive the tail of the multivariate distribution of ’s by setting
’s by setting 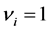
 in the Equation (1.2).
in the Equation (1.2).
With the aid of piecewise deterministic Markov process theory and using the results in [1], the infinitesimal
generator of the process  acting on a function
acting on a function
 within its domain
within its domain  is given by
is given by
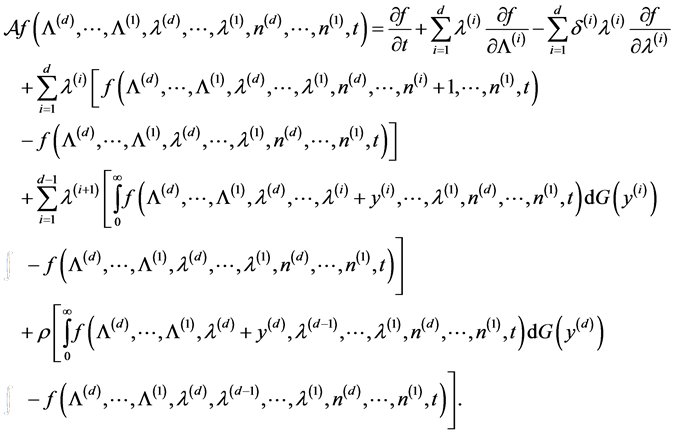 (2.1)
(2.1)
For 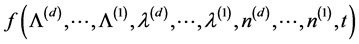 to belong to the domain of the generator
to belong to the domain of the generator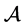 , it is sufficient
, it is sufficient
that 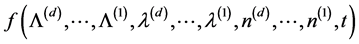 is differentiable w.r.t.
is differentiable w.r.t.
 ,
, 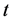 for all
for all 
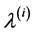 ,
,  ,
, 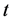 and that
and that
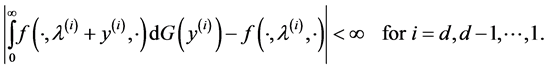
We assume that the Cox processes jumps, intensity jumps and primary event jumps do not occur at the same time.
Let us find a suitable martingale to derive the Laplace transform of the vector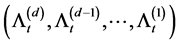 , the
, the
Laplace transform of the vector 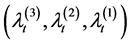 and the p.g.f. (probability generating function) of the vector
and the p.g.f. (probability generating function) of the vector
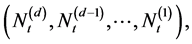 respectively.
respectively.
Theorem 2.1 Considering constants ,
,  and
and 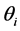 such that
such that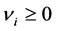 ,
, 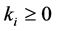 and
and 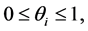
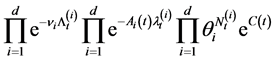 (2.2)
(2.2)
is a martingale, where
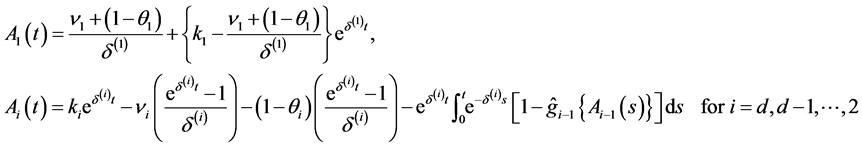
and

where
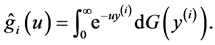
Proof. From (2.1), 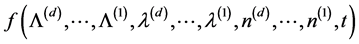 has to satisfy
has to satisfy  for it to be a martin-
for it to be a martin-
gale. Setting

we get the Equation
 (2.3)
(2.3)
from which we have
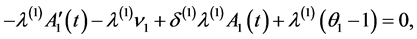

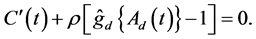
Solve these Equations, then the result follows.
For simplicity, we set  (i.e.
(i.e.  and 1), but it can be easily extended to the higher dimension cases.
and 1), but it can be easily extended to the higher dimension cases.
Theorem 2.2 Let 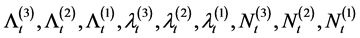 be as defined. Then
be as defined. Then
 (2.4)
(2.4)
where
and 

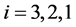
Proof. Using the martingale derived in Theorem 2.1, we have

Hence the result follows immediately if we set
and
in (2.5).
Corollary 2.3 Let
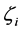

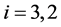
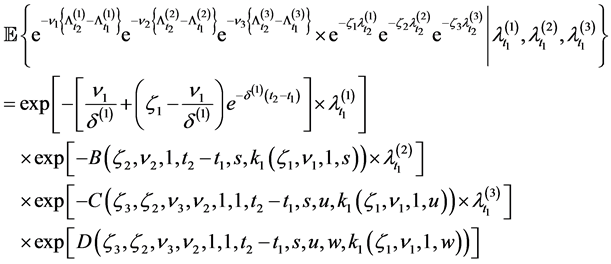
and
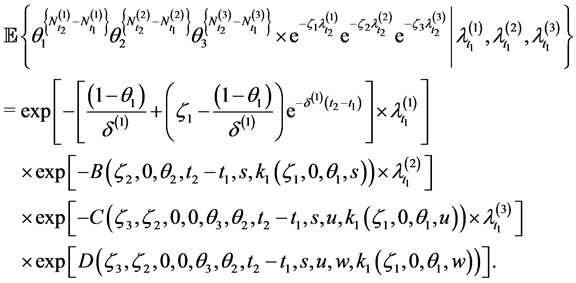
Proof. If we set 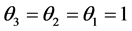

Now we can easily derive the Laplace transform of the vector 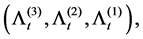
vector 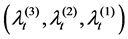
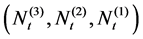
Corollary 2.4 The Laplace transform of the vector 
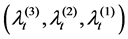

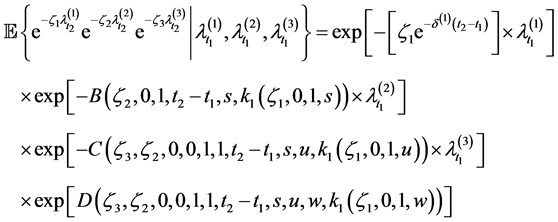
and the p.g.f. of the vector 
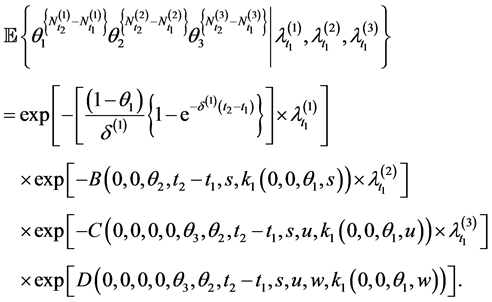
Proof. If we set 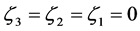


Remark 1: It would be interesting to apply the p.g.f. of the vector 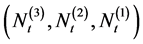
marginal probability generating function for 
found in Dassios and Jang [2,12]. To obtain the mean and variance of the level of water in dams and rivers, the
Laplace transform of the vector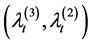
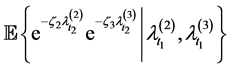
Corollary 2.5 The Laplace transform of the vector
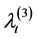

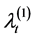

Proof. Let 
3. Multivariate Survival Function
Having derived the Laplace transform of the vector 
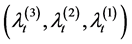
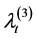

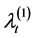
Corollary 3.1 The Laplace transform of the vector 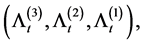
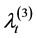

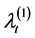
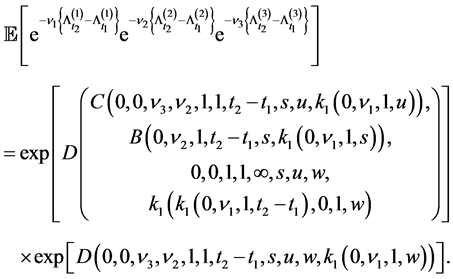
Proof. Take the expectation to (2.8) and use (2.11), then (3.1) follows.
Now, we can obtain the multivariate survival function, other relevant joint distributions and the marginal survival functions.
Corollary 3.2 The multivariate survival function, where
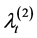
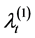
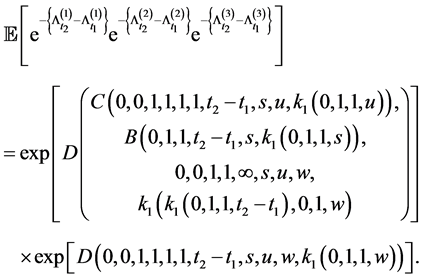
Proof. If we set 
Using (3.2), we can obtain other relevant joint distributions, three bivariate survival functions, i.e.
and other relevant bivariate distributions. We can also obtain three marginal survival functions, i.e.
They are omitted as they can easily be obtained by using the values for the vector 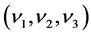
4. Numerical Examples
In this section, we show the calculations of multivariate survival function, other relevant joint distributions and the survival functions, i.e. eight joint distributions, three bivariate survival functions and three marginal survival functions. To do so, we use three exponential distributions for jump sizes for

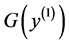
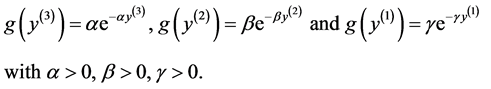
Other distributions such as normal, log-normal, gamma and Pareto, etc. can be also applied for jump size distributions for 
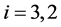
Using (3.2), one of corresponding bivariate survival functions is given by

We can easily obtain other corresponding bivariate survival functions, i.e.
which are omitted as they have similar nested expressions to (4.2).
Using (3.2), one of corresponding marginal survival functions is given by
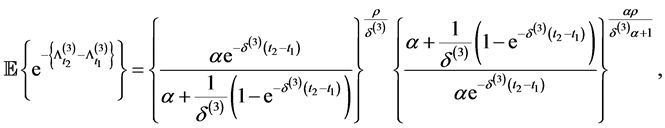
which can be found in Dassios and Jang [2]. We can also find another corresponding marginal survival function, i.e.
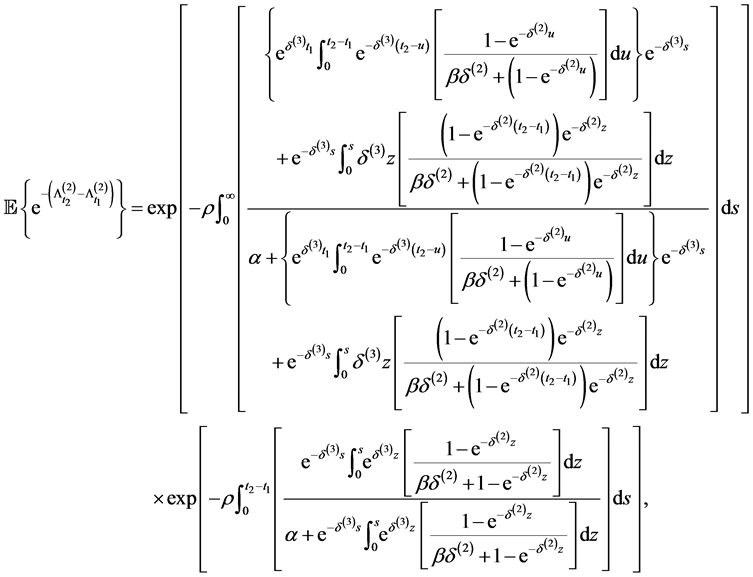
We can easily obtain remaining marginal survival function, i.e. 
Now let us illustrate the calculations of three marginal survival functions, three bivariate survival functions and eight joint distributions. To do so, we use the parameter values as below:
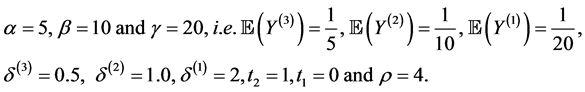
Example 4.1 (Marginal survival functions)
The calculations of three marginal survival functions, i.e.
are given by
Example 4.2 (Bivariate survival functions)
The calculations of three bivariate survival functions, i.e.
are given by
Example 4.3 (Eight joint distributions)
The calculations of eight joint distributions, i.e.
are given by
Remark 2: Example 4.1 shows that the survival probability of the firm 1 is the highest and the firm 2’s and the firm 3’s, which can be modified with different parameter values for (4.5). Example 4.2 and 4.3 show that all relevant joint probabilities are in line with each survival probability in Example 4.1. For example, the joint survival probability of firm 2 and 1, 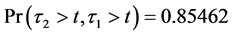

An economic interpretation from the perspective of the multiple shot noise process is the following. After the firm 3 ceases to function (e.g. default of Lehman Brothers), its intensity is still around affecting the other firms in the way of the multiple shot noise process. Hence 
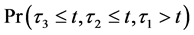
After the failing of the firm 3, 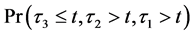
5. Conclusions
We introduced multiple shot noise process, where each process acts as a jump intensity for the next one, and its integral. These two processes can be used in hydropower, dam and river engineering fields. Based on the piecewise deterministic Markov process theory developed by Davis [1] and the martingale methodology used by Dassios and Jang [2], we derived the Laplace transforms of these two processes. Using the multivariate Cox process, the multivariate probability generating function for the number of jumps was also presented. To do so, we have made an assumption that the Cox processes jumps, intensity jumps and primary event jumps are independent of each other. This probability generating function can be considered applying to modeling insurance claim arrivals as well as the number of losses to the entire financial system/market.
Using the Laplace transform of the integral of multiple shot noise process, we obtained the tail of multivariate distributions of the first jump times of the Cox processes, i.e. the multivariate survival functions. These survival functions can be used as the measures to decide whether the government intervention is required to ameliorate the contagious effects to the entire financial system or larger economy. With exponential distributions for jump sizes, we calculated multivariate survival function, other relevant joint distributions and the survival functions. We leave the applications of what we presented in this paper, i.e. a multivariate Cox process with multiple shot noise intensity, multiple shot noise process and its integral to the fields mentioned above for further research.
References
- 1. M. H. A. Davis, “Piecewise Deterministic Markov Processes: A General Class of Non Diffusion Stochastic Models,” Journal of the Royal Statistical Society B, Vol. 46, No. 3, 1984, pp. 353-388.
- 2. A. Dassios and J. Jang, “Pricing of Catastrophe Reinsurance & Derivatives Using the Cox Process with Shot Noise Intensity,” Finance & Stochastics, Vol. 7, No. 1, 2003, pp. 73-95.
http://dx.doi.org/10.1007/s007800200079 - 3. J. A. Smith, “Point Process Model of Rainfall,” Ph.D. Thesis, The Johns Hopkins University, Baltimore, 1980.
- 4. F. Allen and D. Gale, “Financial Contagion,” Journal of Political Economy, Vol. 108, No. 1, 2000, pp. 1-34.
http://dx.doi.org/10.1086/262109 - 5. K.-H. Bae, G. A. Karolyi and R. M. M. Stulz, “A New Approach to Measuring Financial Contagion,” The Review of Financial Studies, Vol. 16, No. 3, 2003, pp. 717-763. http://dx.doi.org/10.1093/rfs/hhg012
- 6. S. Martinez-Jaramillo, O. Perez-Perez, F. Avila-Embriz and F. Lopez-Gallo-Dey, “Systemic Risk, Financial Contagion and Financial Fragility,” Journal of Economic Dynamics & Control, Vol. 34, No. 11, 2010, pp. 2358-2374.
http://dx.doi.org/10.1016/j.jedc.2010.06.004 - 7. A. Dassios, “Insurance, Storage and Point Process: An Approach via Piecewise Deterministic Markov Processes,” Ph.D. Thesis, Imperial College, London, 1987.
- 8. P. Brémaud, “Point Processes and Queues: Martingale Dynamics,” Springer-Verlag, New York, 1981.
- 9. D. R. Cox, “Some Statistical Methods Connected with Series of Events,” Journal of the Royal Statistical Society B, Vol. 17, No. 2, 1955, pp. 129-164.
- 10. J. Grandell, “Doubly Stochastic Poisson Processes,” Springer-Verlag, Berlin, 1976.
- 11. A. Dassios and J. Jang, “Double Shot Noise Process and Its Application in Insurance,” Journal of Mathematics and System Science, Vol. 2, No. 2, 2012, pp. 82-93.
- 12. A. Dassios and J. Jang, “The Distribution of the Interval between Events of a Cox Process with Shot Noise Intensity,” Journal of Applied Mathematics and Stochastic Analysis, 2008, Article ID: 367170. http://dx.doi.org/10.1155/2008/367170