Applied Mathematics
Vol.4 No.10C(2013), Article ID:38420,3 pages DOI:10.4236/am.2013.410A3015
Non-Traveling Wave Solutions for the (1 + 1)-Dimensional Burgers System by Riccati Equation Mapping Approach
College of Science, Lishui University, Lishui, China
Email: msh6209@aliyun.com.cn
Copyright © 2013 Ruiyang Xu, Songhua Ma. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 2, 2013; revised October 2, 2013; accepted October 9, 2013
Keywords: Riccati Equation Mapping Approach; Linear Variable Separation Approach; Burgers System; Non-Traveling Wave Solutions
ABSTRACT
Starting from the symbolic computation system Maple and Riccati equation mapping approach and a linear variable separation approach, a new family of non-traveling wave solutions of the (1 + 1)-dimensional Burgers system is derived.
1. Introduction
Exact solutions of nonlinear partial differential equations (NPDEs) have been of a major concern for both mathematicians and physicists [1-4]. Many efforts have been made on the study of NPDEs [5-8]. In the past few decades, many significant methods have been presented such as Bäklund transformation, Darboux transformation, the extended tanh-function method, and the F-expansion method, Lie group analysis, homogeneous balance method, Jacobi elliptic function method, and the mapping method, etc. [9-15]. The mapping approach is a kind of classic, efficient and well-developed method to solve nonlinear evolution equations, the remarkable characteristic of which is that we can have many different ansatzs and therefore, a large number of solutions. In the past, we have solved the exact solutions of some nonlinear systems via the Riccati equation 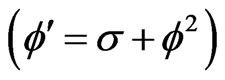 mapping method, such as (1 + 1)-dimensional related Schrödinger equation, (2 + 1)-dimensional Generalized Breor-Kaup system, (3 + 1)-dimensional Burgers system, (3 + 1)- dimensional Jimbo-Miwa system, (2 + 1)-dimensional modified dispersive water-wave system, (2 + 1)-dimensional Boiti-Leon-Pempinelli system, (2 + 1)-dimensional Korteweg de Vries system, (2 + 1)-dimensional asymmetric Nizhnik-Novikov-Veselov system et [16-19]. In this paper, via a mapping equation we find some new non-traveling wave solutions of the (1 + 1)-dimensional Burgers equation:
mapping method, such as (1 + 1)-dimensional related Schrödinger equation, (2 + 1)-dimensional Generalized Breor-Kaup system, (3 + 1)-dimensional Burgers system, (3 + 1)- dimensional Jimbo-Miwa system, (2 + 1)-dimensional modified dispersive water-wave system, (2 + 1)-dimensional Boiti-Leon-Pempinelli system, (2 + 1)-dimensional Korteweg de Vries system, (2 + 1)-dimensional asymmetric Nizhnik-Novikov-Veselov system et [16-19]. In this paper, via a mapping equation we find some new non-traveling wave solutions of the (1 + 1)-dimensional Burgers equation:
 (1)
(1)
2. Non-Traveling Wave Solutions of the Burgers System
As is well known, to search for the solitary wave solutions for a nonlinear physical model, we can apply different approaches. One of the most efficient methods of finding soliton excitations of a physical model is the socalled mapping approach. The basic ideal of the algorithm is as follows. For a given nonlinear partial differential equation (NPDE) with the independent variables 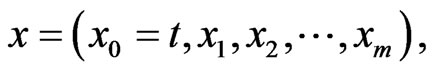 and the dependent variable
and the dependent variable , in the form
, in the form
 (2)
(2)
where  is in general a polynomial function of its arguments, and the subscripts denote the partial derivatives, the solution can be assumed to be in the form
is in general a polynomial function of its arguments, and the subscripts denote the partial derivatives, the solution can be assumed to be in the form
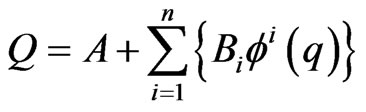 (3)
(3)
with
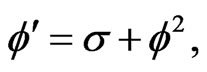 (4)
(4)
where 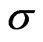 is a constant and the prime denotes the differentiation with respect to
is a constant and the prime denotes the differentiation with respect to . To determine
. To determine 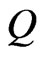 explicitly, one may substitute (3) and (4) into the given NPDE and collect coefficients of polynomials of
explicitly, one may substitute (3) and (4) into the given NPDE and collect coefficients of polynomials of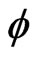 , then eliminate each coefficient to derive a set of partial differential equations of
, then eliminate each coefficient to derive a set of partial differential equations of  and
and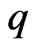 , and solve the system of partial differential equations to obtain
, and solve the system of partial differential equations to obtain  and
and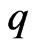 . Finally, as (4) is known to possess the solutions
. Finally, as (4) is known to possess the solutions
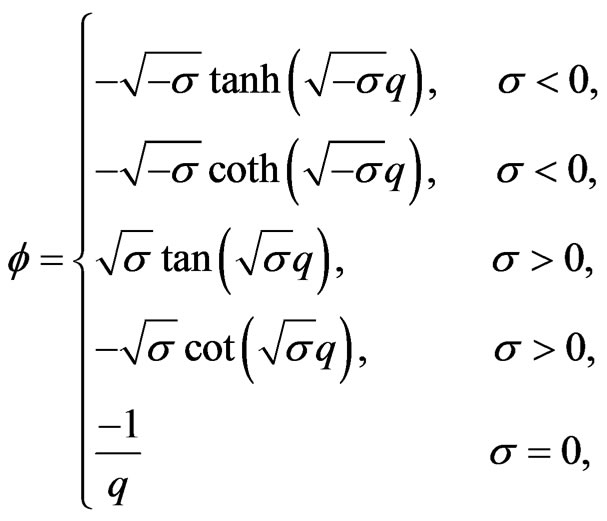 (5)
(5)
Substituting 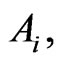
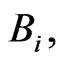
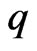 and (5) into (3), one obtains the exact solutions to the given NPDE.
and (5) into (3), one obtains the exact solutions to the given NPDE.
Now we apply the projective equation approach to (1). By the balancing procedure, the ansatz (3) becomes
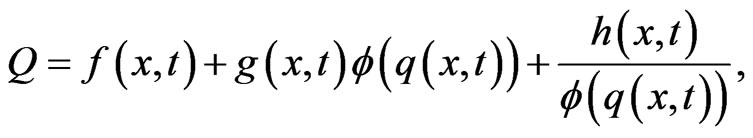 (6)
(6)
where  and
and 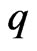 are functions of
are functions of 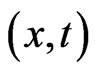 to be determined. Substituting (6) and (4) into (1) and collecting coefficients of polynomials of
to be determined. Substituting (6) and (4) into (1) and collecting coefficients of polynomials of , then setting each coefficient to zero, we have
, then setting each coefficient to zero, we have
 (7)
(7)
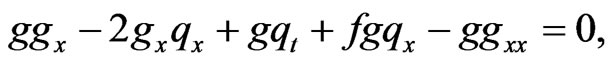 (8)
(8)
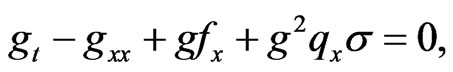 (9)
(9)
 (10)
(10)
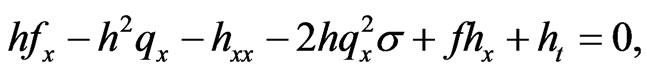 (11)
(11)
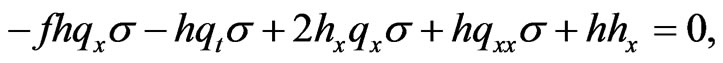 (12)
(12)
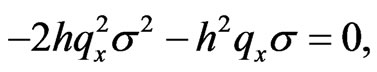 (13)
(13)
Based on (7), (13) and (8), we have
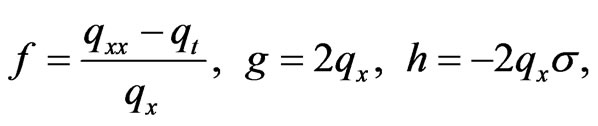 (14)
(14)
with
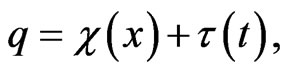 (15)
(15)
where 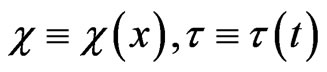 are two arbitrary variable separation functions of
are two arbitrary variable separation functions of  and of
and of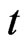 , respectively. Based on the solutions of (4), one thus obtains following exact solutions of Equation (1):
, respectively. Based on the solutions of (4), one thus obtains following exact solutions of Equation (1):
 (16)
(16)
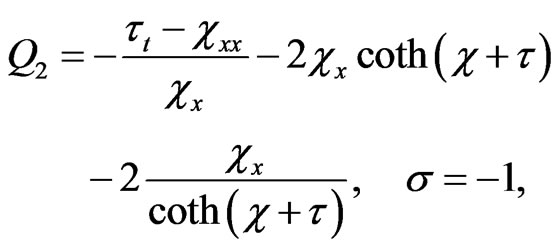 (17)
(17)
 (18)
(18)
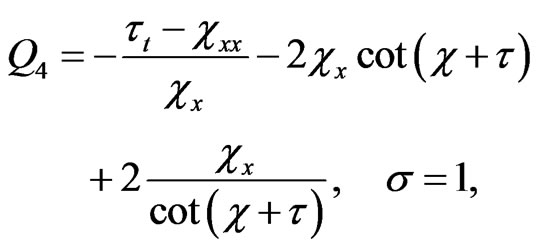 (19)
(19)
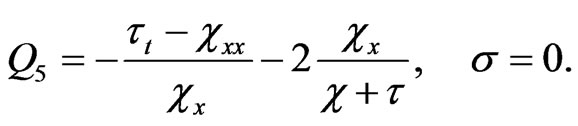 (20)
(20)
3. Summary and Discussion
In summary, with the help of a projective equation  and a linear variable separation method, we find some new exact solutions of the (1 + 1)-dimensional Burgers system. Because of wide applications of the Burgers equation in physics, more properties are worthy to be studied such as its Lax pair, symmetry reduction, bilinear form, and Darboux transformation, etc. All these properties are worthy of studying further.
and a linear variable separation method, we find some new exact solutions of the (1 + 1)-dimensional Burgers system. Because of wide applications of the Burgers equation in physics, more properties are worthy to be studied such as its Lax pair, symmetry reduction, bilinear form, and Darboux transformation, etc. All these properties are worthy of studying further.
4. Acknowledgements
The authors would like to thank Professor S. Y. Lou for his fruitful and helpful suggestions. This work has been supported by the Natural Science Foundation of Zhejiang Province (Grant Nos. Y6100257, Y6110140, Y6090545).
REFERENCES
- S. Y. Lou and X. Y. Tang, “Fractal Solutions of the Nizhnik-Novikov-Veselov Equation,” Chinese Physics Letters, Vol. 19, No. 6, 2002, pp. 769-771. http://dx.doi.org/10.1088/0256-307X/19/6/308
- S. Y. Lou and X. B. Hu, “Infinitely Many Lax Pairs and Symmetry Constraints of the KP Equation,” Journal of Mathematical Physics, Vol. 38, No. 6, 1997, Article ID: 6401. http://dx.doi.org/10.1063/1.532219
- X. Y. Tang and S. Y. Lou, “Localized Excitations in (2+ 1)-Dimensional Systems,” Physical Review E, Vol. 66, No. 4, 2002, Article ID: 046601. http://dx.doi.org/10.1103/PhysRevE.66.046601
- S. Wang, X. Y. Tang and S. Y. Lou, “Soliton Fission and Fusion: Burgers Equation and Sharma-Tasso-Olver Equation,” Chaos, Solitons and Fractals, Vol. 19, No. 1, 2004, pp. 231-239. http://dx.doi.org/10.1016/j.chaos.2003.10.014
- P. A. Clarkson and M. D. Kruskal, “New Similarity Reductions of the Boussinesq Equation,” Journal of Mathematical Physics, Vol. 30, No. 10, 1989, Article ID: 2201. http://dx.doi.org/10.1063/1.528613
- S. Y. Lou and X. Y. Tang, “Conditional Similarity Reduction Approach: Jimbo-Miwa Equation,” Chinese Physics B, Vol. 10, No. 10, 2001, p. 897. http://dx.doi.org/10.1088/1009-1963/10/10/303
- D. J. Zhang, “The N-Soliton Solutions of Some Soliton Equations with Self-Consistent Sources,” Chaos, Solitons and Fractals, Vol. 18, No. 1, 2003, pp. 31-43. http://dx.doi.org/10.1016/S0960-0779(02)00636-7
- E. G. Fan, “Extended Tanh-Function Method and Its Applications to Nonlinear Equations,” Physics Letters A, Vol. 277, No. 4-5, 2000, pp. 212-218. http://dx.doi.org/10.1016/S0375-9601(00)00725-8
- H. Stephen,” Differential Equations: Their Solutions Using Symmetries,” Cambridge University Press, Cambridge, 1990. http://dx.doi.org/10.1017/CBO9780511599941
- M. B. Abd-El-Malek and M. M. Helal, “Characteristic Function Method for Classification of Equations of Hydrodynamics of a Perfect Luid,” Journal of Computational and Applied Mathematics, Vol. 182, No. 1, 2005, pp. 105-116. http://dx.doi.org/10.1016/j.cam.2004.11.042
- L. J. F. Broer, “Approximate Equations for Long Water Waves,” Applied Scientific Research, Vol. 31, No. 5, 1975, pp. 377-395. http://dx.doi.org/10.1016/j.cam.2004.11.042
- D. J. Kaup, “Finding Eigenvalue Problems for Solving Nonlinear Evolution Equations,” Progress of Theoretical Physics, Vol. 54, No. 1, 1975, pp. 72-78. http://dx.doi.org/10.1143/PTP.54.72
- L. Martinez, “ Schrodinger Spectral Problems with Energy-Dependent Potentials as Sources of Nonlinear Hamiltonian Evolution Equations,” Journal of Mathematical Physics, Vol. 21, No. 9, 1980, pp. 2342-2349. http://dx.doi.org/10.1063/1.524690
- B. A. Kupershmidt, “Mathematics of Dispersive Water Waves,” Communications in Mathematical Physics, Vol. 99, No. 1, 1985, pp. 51-73. http://dx.doi.org/10.1007/BF01466593
- M. M. Helal, M. L. Mekky and E. A. Mohamed, “The Characteristic Function Method and Its Application to (1 + 1)-Dimensional Dispersive Long Wave Equation,” Applied Mathematics, Vol. 3, No. 1, 2012, pp. 12-18. http://dx.doi.org/10.4236/am.2012.31002
- S. H. Ma, X. H. Wu, J. P. Fang and C. L. Zheng, “Chaotic Solitons for the (2 + 1)-Dimensional Modified Dispersive Water-Wave System,” Zeitschrift für Naturforschung A, Vol. 61, No. 1, 2007, pp. 249-252.
- S. H. Ma, J. P. Fang and C. L. Zheng, “Folded Locailzed Excitations and Chaotic Patterns in a (2 + 1)-Dimensional Soliton System,” Zeitschrift für Naturforschung A, Vol. 62, No. 1, 2008, pp. 121-126.
- S. H. Ma, J. Y. Qiang and J. P. Fang, “The Interaction between Solitons and Chaotic Behaviours of (2 + 1)-Dimensional Boiti-Leon-Pempinelli System,” Acta Physics Sinica, Vol. 56, No. 2, 2007, pp. 620-626.
- S. H. Ma, J. P. Fang and H. P. Zhu, “Dromion Soliton Waves and the Their Evolution in the Background of Jacobi Sine Waves,” Acta Physics Sinica, Vol. 56, No. 8, 2007, pp. 4319-4325.

