ABSTRACT

We review (not exhaustively) the quantum random walk on the line in various settings, and propose some questions that we believe have not been tackled in the literature. In a sense, this article invites the readers (beginner, intermediate, or advanced), to explore the beautiful area of quantum random walks.

Keywords:

Quantum Walk, Decoherence, Entanglement, Phase Parameters, Localization, Disorder, Inhomogeneity, Memory

1. Introduction

1.1. Preamble

The author would first like to thank Scientific Research Publishing with the invitation to contribute to the special issue on “Stochastic Processes”. I also acknowledge all active researchers in “Quantum Wonderland”.

The quantum walk (QW) is regarded as the quantum analogue of the random walk (RW). In the RW, a particle is located at one of a set of definite positions (such as the set of integers on the line). In response to a random event―for example, the flipping of a coin―the particle moves either left or right. This process is iterated, and the motion of the particle is analyzed statistically. These systems provide good models for diffusion and other stochastic processes. The QW is studied in various contexts and settings. The main difference between the RW and the QW can be simply stated in terms of the dynamics on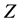, the integers. In the RW, the walker is in position at time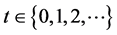, and moves to 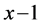at time 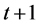with probability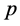, or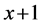, with probability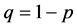. 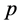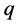In contrast, the evolution of the quantum walker is defined by replacing and with 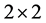matrices 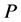and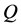, respectively, where 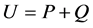is unitary. If 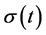denotes the standard deviation of the walk at time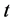, then it is well known that the particle spreading in the classical case is diffusive, , while in the quantum case, the particle spreading is ballistic,. In quantum computation, the QW is applied to quantum algorithms and is known to give faster searching than the classical random walk, e.g., the Grover walk which is related to the Grover search algorithm.

In these notes we have touched on some major topics on the QW that has been the subject of extensive research by many authors from the experimental and theoretical point of view. It is my hope that the reader at any level interested in research on the QW, will take this opportunity to read these notes, and explore some of the questions we have proposed here, as an initiation into “Quantum Wonderland”.

A good working knowledge of probability, statistics, linear algebra, and analysis, is a prerequisite necessary to commence research on the QW. Aside, motivation, passion, mathematical maturity, and the ability to think in abstract and applied terms, are also key ingredients to becoming a successful researcher in this area.

Apart from the books mentioned in these notes, the following books make it possible for the reader with a good working knowledge of probability, statistics, linear algebra, and analysis, to start reading the research papers on QW in the literature:

・ Nielsen and Chuang, Quantum Information and Quantum Computation, Cambridge University Press (2011).

・ Portugal, Quantum Walks and Search Algorithms, Springer (2013).

・ Wang and Manouchehri, Physical Implementation of Quantum Walks, Springer (2013).

・ McMahon, Quantum Computing Explained, Wiley-IEEE Computer Society Pr (2007).

1.2. Introduction on the Quantum Walk

The quantum walk [1] is regarded as the quantum analogue of the classical random walk [2] . The quantum walk can be divided in two parts, the discrete [3] [4] and the continuous [5] [6] . The time evolution of the quantum walk can either be discrete [7] or continuous [6] . The connection between the continuous time quantum walk and the discrete time quantum walk has been established, see [8] - [10] for examples. The walk is intensely investigated in the literature due to its connection to quantum computing, see [11] - [20] for examples. In particular quantum walks have shown promise in the design of quantum algorithms [21] , and the proposals in the literature are becoming extensive, see [22] - [31] for examples. The experimental implementation and realization of the quantum walk is also receiving considerable attention in the literature by researchers. Experiments are being designed and in some cases already performed to implement the quantum walk, see [32] - [40] for examples. The quantum walk is studied on various topologies including cycles, lattices, and hyper-cubes. The literature is extensive; a few examples include the authors in [41] - [50] . For the most comprehensive review on the quantum walk, the reader should consult [51] . Another nice review is given in [52] . As far as books are concerned the reader should consult the following references [53] - [56] .

1.3. Introduction on Disorder

The discrete-time quantum walk with spatially or temporally random defects as a consequence of interactions with random environments is known as the disordered quantum walk. In this paper we review the disordered quantum walk as defined by N. Konno [57] . We should remark that the unitary transformation governing our walk is an example of a disordered quantum walk of type II. The matrix was studied by Mackay et al. [58] in their analysis of quantum walk in higher spatial dimensions, comparing classical and quantum spreading as a function of time. As for the review on disorder in quantum systems, beginning in [59] the authors study the transport efficiency of an excitation moving from a source via a network to a drain. The model considered is a topologically disordered network with long-range interactions of dipole-dipole type. The authors show the crossover between purely quantum mechanical transport and environmentally induced diffusion, by phenomenologically modeling the system using quantum stochastic walk. In [60] , the authors study quantum walks where signals can jump to a distant location, which is a generalization motivated by Levy flights in classical mechanics. In particular, they study two classes of quantum walks with disordered connections between beam-splitters. In the particular case of dynamic disorder, the model considered shows that decoherence leads Gaussian distribution modulated by residual patterns of quantum walk or by valleys. In [61] , the authors investigate excitonic transport in systems consisting of rings of chromophores stacked in cylindrical arrays, as a function of the number of chromophores per ring, the spacing between rings, and the strength of decoherence and disorder. Using the symmetries of the system, the authors perform simulations to capture the dynamics of excitonic diffusion in the presence of environmentally-induced noise and disorder. In particular, the authors provide clear evidence for the presence of super transfer in the appropriate regimes and for the destruction of super transfer in other regimes. In [62] , the authors investigate one-dimensional discrete time quantum walks with spatially or temporally random defects as a consequence of interactions with random environments. In particular the authors show that quantum walks with spatial disorder exhibit delocalization behaviors. In [63] , the author studies the discrete-time quantum walk model with Hamiltonian form of the evolution operator for each step. In particular, studying the walk dynamics using temporal, spatially static, and fluctuating disordered unitary evolutions, it is shown that localization only occurs with spatially static disordered operations. Anderson localization usually emerges in quantum systems when randomized parameters cause the exponential suppression of motion. In [64] this phenomenon is considered using the toric code. The authors show that magnetic field perturbations on the toric code induce quantum walks of anyons, which quickly destroy any stored information when anyons are present. In particular, they show that disorder induces exponential localization which suppresses the anyon motion. In [65] , the authors study how disorder and fluctuations in a periodic lattice can influence the evolution of a transversing particle. In particular they show a fast ballistic spread for slowing changing lattice parameters, a diffusive spread in the case of dynamical disorder, and Anderson localization for lattices with static disorder. In [66] the authors study a spin (one-half)-particle on a one dimensional lattice subject to disorder induced by a random, space-de- pendent quantum coin. The discrete time evolution is given by a family of random unitary quantum walk operators, where the shift operation is assumed deterministic. Sufficient conditions on the probability distribution of the coins such that the system exhibits dynamic localization is derived. In [67] , the author presents an approach to induce localization of a Bose-Einstein condensate in a one-dimensional lattice under the influence of unitary quantum walk evolution using disordered quantum coin operation. It is shown that the discrete-time quantum walk on a two-state particle in a one-dimensional lattice can be diffused or strongly localized in position space, respectively. In addition, it is shown that these behaviors of the discrete time quantum walk can be efficiently induced without introducing decoherence into the system. In [68] the authors consider percolation lattices, as a simple example of a disordered system, in which edges or sites are randomly missing, interrupting the progress of the quantum walk. In one dimension quantum tunneling is used study the properties of the quantum walk as it spreads, whilst in two dimensions, it is shown that spreading rates vary from linear in the number of steps down to zero, as the percolation probability decreases towards the critical point. In [69] the dynamics of finite-sized disordered systems is considered, using the mapping between any master equation satisfying detailed balance and a Schrodinger equation in configuration space, the authors compute the largest eigenvalue relaxation time of the dynamics via lowest energy vanishing eigenvalue of the corresponding quantum Hamiltonian. In [70] the fate of quantum walks in a random environment is studied, with both static and dynamic disorder. It is shown that static disorder is responsible for exponentially suppressing quantum evolution with variance reaching a time-independent limit for long times, depending on the strength of static disorder and space dimensionality. For dynamic disorder, by coupling the quantum system to a random environment it is shown that decoherence occurs and quantum physics becomes classical so that a quantum walk is still propagating but only diffusively. In [71] the effect of static disorder on the coherent exciton transport by means of discrete Wigner functions is analyzed. It is shown that the Wigner function shows strong localization about the initial node. Integrating out the details of the time evolution by considering the long time average of the Wigner function, it is shown that localization is even more pronounced. In [72] the authors study the effect of random and aperiodic environments on cooperative processes in one space dimension. It is shown that at the critical point, both for the transverse-field Ising model and for the diffusion process, the two types of in homogeneities have quite similar consequences, which is based on the same type of distribution of the low energy excitations. Finally in [73] , the authors study controllability of a closed quantum system whose dynamical lie algebra is generated by adjacency matrices of graphs. The key property is a novel graph-theoretic feature consisting of a particularly disordered cycle structure. The main result is characterizing a large family of graphs that give a pair of Hamiltonians implementing any quantum dynamics, thereby rendering a system controllable.

1.4. Introduction on Inhomogeneity

When the quantum walk is position dependent it is said to be inhomogeneous. The inhomogeneous quantum walk is studied in various settings, especially in the applications. In [74] a two-state time inhomogeneous quantum walk is defined by two matrices on the line. It is shown that for the time-homogeneous walk determined by a unitary matrix, the limit distribution is expressed by a single density function. However, if another unitary matrix operates the walk in certain intervals, the limit distribution has a combination of density functions. In [75] the authors focus on the localization property of the quantum walk and study a class of the discrete-time quantum walk (DTQW) on a one-dimensional lattice with spatially homogeneous coins. Localization is defined as the limit distribution of the DTQW divided by some power of the time variable has the probability density given by the Dirac Delta function. Let be the position of the walker, the coin flip is given by

.

In [76] the authors study walks that are periodic in position and show that depending on the period, such

walks can be bounded or unbounded. The coin flip used in [76] is related to those in [75] by. Given a sequence, with, let. It is shown in

[77] that ballistic and localized behaviors in the walk co-exist with respect to the time average measure and the weak limit measure. A universality class of quantum walks with respect to the weak limit measure is also proposed. In [78] the case is treated. Using the method of path counting, the quenched and annealed weak limit theorems for the walk is presented. On the other hand the case is treated in [79] , in which it is shown that the walk exhibits localization by a path counting method. In [80] we treated and obtained the limit theorem for the walk using the Fourier analysis.

1.5. Introduction on Parametrization

As far as we can tell the quantum walk on the line with phase parameters was initiated by Villagra et al. [81] . In this paper the authors study a discrete-time coined quantum walk on the line with the objective of addressing the following question: Given a graph, what is the probability that a quantum walk arrives at a given vertex after some number of steps? The main contribution of the paper is a closed-form formula for a general symmetric SU(2) operator for walks on the line. In the quantum walk on the line the operator is defined as follows: Take any unitary operator, and form the unitary operator, where is the diagonal phase adjustments with. Due to the restriction of to the unit interval, the author of the present paper started calling walk operators of the form the parametrization of, in analogy to parametric equations in mathematics. The parametrization of the quantum walk has been investigated, and the contributions are few. In [82] we investigated the question above for the Grover operator by proposing a coin operation with phase parameters. We studied the discrete-time quantum walk on the line and obtained a closed- form formula for the amplitudes of the state of the walk and convergence properties of the walk. In [83] we studied asymptotic entanglement properties of the Hadamard walk with phase parameters on the line using the Fourier representation. We used the von Neumann entropy of the reduced density operator to quantify entanglement between the coin and position degree of freedom. We investigate obtaining exact expressions for the asymptotic entropy of entanglement, for different classes of initial conditions. In [84] we obtained the limiting distribution of the Grover walk with phase parameters. In [85] we studied the discrete-time nearest-neighbor quantum walk with phase parameters in random environments in one dimension involving a Grover-type operator. Using the Fourier analysis, we obtained the limiting distribution of the walk.

1.6. Introduction on the Quantum Walk with Memory

Recently Mc. Gettrick [86] introduced and investigated 2-state QW with one step memory on. In [87] the authors show that his walk becomes a 4-state QW by relabeling his notation, which is the definition considered in this paper. In particular any extended version of his walk with -state memory can be considered -state QW without memory. The -state QW has been investigated for specific, for introductory papers, see [88] for the 3-state Grover walk, and for 4-state models, see [89] - [92] .

1.7. Introduction on Decoherence and Entanglement

As is well known the physical implementation of the quantum walk faces many obstacles including environmental noise and imperfections collectively known as decoherence. The decoherence in the quantum walk is intensely investigated in the literature in various settings and contexts, and the overarching goal is to study possible routes to classical behavior. In [93] they gave two such ideas, the first is to measure the quantum “coin” at every step, the record of the measurement outcomes singles out a particular classical path. By averaging over all possible measurement records, one recovers the usual classical behavior. Alternatively, rather than using the same coin every time, one could replace it with a new quantum coin for each flip. After a time one would have accumulated coins, all of them entangled with the position of the particle. By measuring them, one could reconstruct a unique classical path; averaging over the outcomes would once again produce the classical result. For the quantum walk on the line it is known that the variance grows quadratically with time. The variance in the classical random walk on the line, by contrast, grows linearly with time. Both of these are effects of interference between the possible paths of the particle.

Some introductory studies on the decoherent quantum walk can be found in [94] - [118] and have been reviewed by the author of the present paper in [119] . In [93] , the decoherent quantum random walk on the 1-di- mensional integer lattice is studied, leading to expressions for the first and second moments of the position distribution, it is also shown in the long time limit that the variance grows linearly with time with the diffusive character. In [119] the Brun type decoherence is extended to the two dimensional setting providing generalizations with wide range of applications. The generalized first and second moments for the decoherent quantum walk is obtained, the Brun formalism for the quantum walk is also treated. In the presence of broken line noise, the diffusive character of the walk is studied. It is conjectured that the diffusion coefficient in the quantum realm varies directly as, and inversely as, where is the probability of adjacent broken link at a given site in the walk. The conjecture if holds true implies the diffusion co-efficient of the decoherent quantum walk is always larger than the diffusion co-efficient in the in the classical case.

As the author of the present paper pointed out in [119] , due to the complexity of the calculations, the pure analytic papers on the decoherent quantum walk have been given little attention in the literature. Moreover in [120] it is found that the complicated form of the superoperator in [93] makes it difficult to obtain the limit of the decoherent quantum walk. However, this difficulty is overcome by analyzing the characteristic function of the position probability distribution.

In this paper we follow the convention of obtaining the limit of the decoherent quantum walk by analyzing the characteristic function, following discussion of the result of Fan et al. [120] , which was recently extended in the two-dimensional setting by the author of the present paper [119] .

Related to decoherence is the notion of entanglement. The (asymptotic) entanglement in quantum walks is intensely investigated in the literature in various context, see [121] - [149] , for examples. In this paper we also review asymptotic entanglement of the quantum walker in the sense of Machida [150] . The discussion of their result indicates application to entanglement rather than decoherence. Quantifying entanglement has been considered in various contexts [151] - [160] . If the system is pure, the von Neumann entropy is used as a measure to quantify the entanglement. The measure of entanglement in this case is usually given by,

where is the reduced density operator obtained from by tracing over the po-

sition degrees of freedom. We should remark that studies involving this measure of entanglement have focused mainly where has dimension two, see [161] - [163] for examples, the case where has dimension higher than two has been given little attention in the literature, the known studies in this case include [164] [165] .

2. Brief Overview of the Quantum Random Walk on the Line

In the general setting the time-evolution of the one-dimensional quantum walk is given by the following unitary

matrix, where, and is the set of complex numbers. The unitarity of implies we have, , , , where the bar denotes complex conjuga-

tion, and with. The quantum walk is regarded as the quantum analog of the classical random walk with an additional degree of freedom called the chirality. The chirality takes value left and right, and means the direction of the motion of the particle. The evolution of the quantum walk takes place in the following way. At each time step if the particle has the left chirality, it moves one step to the left, and if it has the right chirality, it moves one step to the right. The unitary matrix acts on two chirality states and:

;. Put, and, then:;

. In particular, at any time, the amplitude of the location of the particle is defined by a 2-component vector in at each location. The probability that the particle is at location is given by the square of the modulus of the vector at. If defines the amplitude at time at

location where, with the chirality being left (upper component) or right (lower component), then the dynamics of the quantum walk is given by the following transformation:

,

where

,.

We should remark that, and the unitarity of ensures that the amplitude always defines a probability distribution for the location. The probability that the quantum walker is in position at time is given by

,

where. In the -space we have. By the inverse Fourier transform we have. In the -space the time evolution of the walk is given by. From and induction on, we can write the time evolution of the walk by, where is the initial state in the Fourier domain. Note that we can write the probability distribution as. The explicit form of the probability distribution is given by the Konno density function.

Theorem 1 (Konno Density Function): Consider the one-dimensional quantum walk at time starting from the initial quibit state with, determined by the unitary matrix with, where, and is the set of complex numbers.

If, then, where has the density with, for, and for.

Remark 2: We are referring to the probability distribution in Theorem 1, in the sense of weak limit theorem.

The weak limit theorems for quantum random walks have a storied history. In fact going back to Grimmett, Janson, and Scudo [167] , they formulate and prove a general weak limit theorem for quantum random walks in

one or more dimension. In particular, let denote position at time, the authors show that converges

weakly as to a certain distribution which is absolutely continuous and of bounded support. In the one-dimensional setting the authors obtained the following result.

Theorem 3: If, then, where is a random variable of with distribution.

Proof/Sketch of Proof: Let be the unitary matrix governing the quantum walk in the one dimensional setting in the Fourier picture. Suppose and are the eigenvalues and eigenvectors of, respectively. Put

,

then

,

where. It can be shown that

.

Combining the expressions for and yields, as,

.

Let, let be the probability measure on given by

on.

Let, and define by, then. Since is bounded and the relation holds for all, by the method of moments the result follow.

The authors further extend Theorem 3 to arbitrary dimension using the same argument yielding the following result.

Theorem 4: For the -dimensional quantum walk

where is a random element of with distribution, and, where, and.

The papers [167] [168] gave a complete characterization of the weak limit theorem for one-dimensional quantum walks, which is now known as the Konno density function. In particular using an explicit form of

the author obtained the characteristic function of and the moment of it. From the explicit form of the author obtained a combinatorial expression for the characteristic function of

and used it to obtain the limit theorem of.

The weak limit theorem can also be written in terms of the density matrices at position at time [150] . In particular if is the amplitude of the walker at position at time, then the density matrix is given by, and we have the following version of Theorem 1.

Theorem 5: For, and, we have,

where,

,

,

and means the expected value of.

Remark 6: We should note a version of Theorem 5 for the interference terms have been given in [150] . The ground-breaking paper [169] , study the connection of the limit distribution of the interference terms in the continuous-time quantum random walk. From now on, the connection to other notions in quantum information science is discussed.

3. Connection to Notion of Disorder

Consider the time evolution of the quantum walk governed by the following infinite random unitary matrices

, , where the entries of the matrix are complex numbers, and the subscript denotes the time step. The unitary of gives, , , , where denotes complex conjugation, and with. Put.

Let be independent and identically distributed on some space with

and. By using the fact that, , ,

, we also see that and. The set of initial quibit states for the quantum walk is given by, where means the transposed operator.

Moreover, we assume that and are independent. The quantum walk governed by the above process is what is called the disordered quantum walk. In this paper we will consider quantum walks de-

scribed by the above process with the additional requirement that, and.

4. Connection to Notion of Parametrization

Let

,.

The state of the walk at time is defined over the joint space

,

where

,

and is the amplitude at time in direction and position. We should note that

.

For the analysis of the walk on line we consider the projection at time onto position as two dimensional vector in

:,

where and represent the amplitude of the walker at position at time going left and

right respectively. The probability of being at position at time is given by. In this paper we will take and for , with The time

evolution of the walk is given by. By induction on, we can show in terms of, the evolution is given by, where is a unitary defined on, is the identity operator on and is the coin operator in the usual quantum walk acting on, and is the shift operator. It should be noted that the quantum walker first choose a direction of movement using the coin operator in the usual quantum walk and moves according to the operator

.

Let be the coin operator in the usual quantum walk. In the quantum walk with phase parameters we replace the coin operator with, where is the diagonal phase adjustment with.

Let

, ,

, and,

then

,

with the following effect on:. The dynamics of the quantum walk is given by

,

where

,

and

.

5. Connection to Notion of Inhomogeneity

In the general setting, the time evolution of the walk is determined by a sequence of unitary matrices, , where

,

with. The subscript indicates the location. The matrix rotates the chirality before the displacement, which defines the dynamics of the walk. To describe the evolution of the walk, we write, with

and

.

It should be noted that and represent the walker moving to the left and right at position at each time step.

6. Connection to Notion of Decoherence

Here we will discuss two approaches, the first by Fan et al. [120] , and in terms of the interference phenomena, the approach by Machida [150] . Regarding the approach by Fan et al. [120] , we make the discussion in the two dimensional setting, following a recent paper of the author [170] .

6.1. Approach by Fan et al. Discussion in Two-Dimensional Setting

Consider the quantum random walk on the general square lattice. Let the state space be given by, where denotes the position space and denotes the coin space. Let the basis for the position space be given by, and let the basis for the coin space be given by, where represent the left, right, upward, and downward chirality states respectively. Let the shift operators in be defined as follows:

, , ,

and

,

where are unitary shift operators on the particle position. Let be the orthogonal projections on the coin space spanned by

,

where

.

Let be the unitary transformation on, then the evolution operator of the quantum walk is given by

.

The eigenvectors of are given by

,

with eigenvalue

, , ,.

Therefore in the basis (aka Fourier Picture, Fourier Domain) the evolution operator is given by

where

.

We should remark that is also a unitary operator.

Let be a set of unital operators on, that is,. The decoherence on the coin subspace is

defined as follows, before each unitary transformation acting on the coin, a measurement given by the unital operators is performed on the coin, after which a density operator on is transformed by

.

The general density operator of the quantum random walk is given by

,

where

,

and is a vector space of linear operators on. After one step of the evolution introduced by the decoherent coin space, the density operator can be written as

.

Suppose the quantum walk starts in, then the density operator in the initial state is given by

.

After steps the state evolves to

,

where is defined by

for every. The probability of being at at time, is given by

Let be the characteristic function of. The purpose of this section is to obtain the limit theorems for the decoherent quantum walk. We should remark that

where we have used the following property of the dirac delta function

.

Let be any initial state. The generating function of is given by

where and. Note that the generating function is well defined by Lemma 1 below.

We should remark that the proof is similar to Lemma 3.1 in Fan et al. [120] , therefore we omit it.

Lemma 1: Suppose, and is a set of unital operators. Let be an eigenvalue of, then.

We should remark from Lemma 1 that converges inside, and has no poles inside the disk. By Lemma 1 and we have for some. Since a basis for is given by

,

where, , , and are the Pauli matrices. We can write as a linear combination of the basis

elements. In column form let us write

.

Let be the matrix associated with, then,

,

where is the cofactor of. Note that with the exception of, the traces of the other Pauli matrices are zero. Since the elements in the basis are in a tensor product, the decomposition implies the trace of is four, whilst the traces of the other matrices is zero. Hence when taking the trace in

,

only the first row action remains. Therefore we have. Let be the matrix representation of in terms of the basis for, then we have

the following lemma whose proof is similar to Lemma 3.2 in Fan et al. [120] , therefore we omit it. We should remark that in Lemma 2 below we have given the matrix representation for in terms of the tensor product of the matrix representation for as given in Lemma 3.2 of the paper of Fan et al. [120] . However to get the matrix in Lemma 2 below in terms of, one can use the following relation between and

.

We should remark that the proof of Lemma 3.2 in Fan et al. [120] is incomplete, however to get the remaining entries, , it is necessary only to repeat the argument in their proof for each row and/or column with respect to the basis.

Lemma 2: Suppose, and is a set of unital operators, then has the following representation.

.

Let us define the probability mass function on by,.

The limit theorem for the decoherent two-dimensional quantum walk is given by the following:

CLAIM: converges in distribution to a continuous convex combination of normal distributions.

Proof of Claim: [C. Ampadu, Quantum Inf Process (2012) 11: 1921-1929]

6.2. Approach by Machida

Consider the special unitary matrix for the 2-state QW on the line with, and, or, and, where, and. We may suppose

that is the amplitude of the walker at position at time, and are

the density matrices at position at time. Put, and, where denotes the transposed operator. Consider the off-diagonal parts in the density matrices, then the rela-

tion between the interference terms and the moments of are given as follows.

Lemma 1: For, we have

,

where denotes the real part of the complex number.

Proof: [T. Machida, Quantum Information and Computation, Vol.13 No.7 & 8, pp. 661-671 (2013)].

On the other hand, if we assume that the 2-state quantum walk, starts from the origin with the initial state given by, where denotes the transposed operator, and, then the limit theorem is obtain as follows.

Theorem 2: For, we have

,

where

,

where denotes the imaginary part of the complex number, and.

Proof: [T. Machida, Quantum Information and Computation, Vol. 13 No. 7&8, pp. 661-671 (2013)].

7. Connection to Notion of Memory

In this section we define the 4-state quantum walk (4QW) without memory. The state space of the 4-state quantum walk is composed of the following vectors:, , , , where. For the chirality

states we put, , , and,

where denotes the transposed operator. We should remark that, correspond to the left mover, and, correspond to the right mover. In particular the states, , , correspond to the movement “rightleft”, “leftleft”, “leftright”, and “rightright”, respectively. The position shift operator is given by

.

The one-step time evolution operator is given by where is the (infinite) identity matrix and

where the nonzero entries of are complex numbers. To define the 4-state quantum walk let, , where is the set of complex numbers, be a (infinite-component) vector which denotes the position of the walker. Here the component of is one , and the others are zero. Let be the amplitude of the walker at position at time. The 4-state QW at time is given by

.

Recalling that and correspond to a left-mover and and correspond to a right mover, we can write, where

and

,

then the evolution of the QW is determined by

.

The probability that the quantum walker is at position at time, is given by

,

where. In order to obtain the limit theorems we introduce the Fourier Transform of as follows:

.

By the inverse Fourier transform we have

.

The time evolution of is given by

where and

.

The standard argument by induction on the time step gives. The probability that the quantum walker is at position at time is defined by

.

8. Open Questions

8.1. Quantum Walk without Memory

Consider the quantum walk on the -dimensional lattice governed by the unitary matrix, where

.

It is an open problem to obtain the limit theorems for the quantum walk for a general and m-state. We should remark that the case was proposed by Konno and Machida [87] , and we believe it is still unsolved.

8.2. Localization in Quantum Walk

Consider the following question: “If, say, a quantum walker which could be a quantum particle exists only at one site initially in some media, perhaps with disorder, will the quantum walker remain trapped with high probability near the initial position?” This phenomenon of the quantum walker is termed Localization.

1) Consider the disordered quantum walk as described in this paper, and evolution in the Fourier picture,

,

where

and

.

It can be shown that none of the eigenvalues are independent of in the Fourier space. Therefore, how can we show non-existence of localization, rigorously?

2) What is the localization criterion for a general -particle quantum walk on a general -dimensional lattice in which the particles are allowed to stay at the same position, in addition to their original degrees of freedom,?

Example (Five-State Quantum Walk): The Hadamard walk as is well known plays a key role in the studies of the quantum walks, thus the generalization of the Hadamard walk is one of the many fascinating challenges. The simplest and well studied example of the Hadamard walk is given by the following unitary matrix

.

The five-state quantum walk is a kind of generalized Hadamard walk in the plane, and differs markedly from the previous studies. The particle ruled by the 5QW is characterized in the Hilbert space which is defined by a direct product of a chirality-state space and a position space spanned by. The chirality states are transformed at each time step by the following unitary transformation:

,

,

,

,

.

Let

be the amplitude of the wave function of the particle corresponding to the chiralities at the position and the time, where denotes the transposition, and is the set of integers. We assume that a particle exists initially at the origin in the plane, then the initial quantum states are determined by

,

where, and is the set of complex numbers. Before we define the time evolution of the wave function, we introduce the following operators:

,

,

,

,

.

Note that if the matrix, say is applied to, then only the component is selected after carrying out the superposition between, , ,. This is also similar for the other matrices, , ,. We now define the time evolution of the wave function and this is given by

One finds clearly that the chiralities correspond to the left, right, neutral, downward, and upward state for the motion. Using the Fourier Analysis we can get the wave function. Notice that the spatial Fourier transform of is defined by

.

In the Fourier domain, the dynamics of the wave function is defined by, where

.

The standard argument by induction on the time step allows us to write the evolution as

.

It can be shown that the strongly degenerate eigenvalue of 1, associated with this model, is a necessary condition for localization, see [88] for similar type conclusion.

8.3. Decoherence and Entanglement in the Quantum Walk

1) Consider discussion of the asymptotic behavior of the quantum walker subject to decoherence in the two dimensional setting [170] following Fan et al. [120] . We have shown that converges to a continuous convex combination of normal distributions, under certain eigenvalue conditions. Consider the spectrum of the superoperator and obtain the necessary and sufficient conditions for the unitary transformation to satisfy the eigenvalue conditions.

2) Consider discussion of the asymptotic behavior of the quantum walker subject to entanglement in the sense of Machida [150] . Can we generalize their characterization of the limit distribution regarding the quantum walker on the D-dimensional lattice? Can we give similar type criterion on other topological structures rather than? What is the relationship between the results of Machida [150] and Fan et al. [120] , if any?

8.4. Parametrization of the Quantum Walk

1) The Grover operator as is well known was first introduced by Moore and Russell in their study of quantum walks on the hypercube [18] . Based on Grover’s diffusion, the operator has elements

,

where

and where is the lattice dimension of the quantum walk. If, that is, , for example, then we get the most studied Grover transformation,

.

In general given an undirected graph, let be the set of vertices and be the set of edges. If there are edges incident to vertex, for all and, then in its most general form the Grover operator is described by the following matrix

.

If has exactly two edges adjacent to it, then becomes. Following the discussion on the

quantum walk with phase parameters in this paper, it is an open question what is the limiting distribution of subject to parametrization?

2) In a paper of Venegas-Andraca [171] , the quantum walk on the line with two entangled coins is investigated, the shift operator (as we shall see in the two-coin framework (2cQW) example below) is similar in nature to the one in that paper, in that depending on the state of the coin, the walker moves left, right or is stalled in either direction at each step. For this type of quantum walk it is shown numerically that localization occurs. In the paper by Liu and Pentulante [172] , the numerical study of Venegas-Andraca is verified theoretically; in particular they show that the occurrence of localized spikes as observed by Venegas-Andraca reflects the degeneracy of the eigenvalues of the time evolution operator in the Fourier picture. In what follows, we are going to propose a problem regarding a general characterization of the limiting distribution for the “2cQW” for entanglement in the coin subspace of the generalized parametrized quantum walk on the line. First we describe the two-coin framework as motivation.

Motivated Example (2cQW): Let the Hilbert space of the entangled coin subspace of the 2cQW be given by , and let the Hilbert space of position subspace of the 2cQW be given by, then the Hilbert space of the system is given by. The state of the 2cQw can be expressed by. Let the entangled coin operator be given by

, where is the coin operator in the single-coin framework which may be any unitary operator acting on a single coin space. The evolution of the 2cQW is determined by the unitary operator, where is identity operator in the position subspace, and the shift operator which is a three-direction shift operator is given by

We should remark the labeling, where corresponds to the chirality states right, stall right or stall left, and left respectively. On one step of the quantum walk we first make superposition on, and then move the walker according to the coinstate using the shift operator. The state of the

particle at time is given by. In terms of the initial state, the evolution of the walk is given by. Moreover, the probability of finding the particle at position at time is given by. Now we introduce the Fourier transform of the wave function for the “2cQW”. Let

be the amplitude of the wave function, where, , , and

correspond to the chirality states right, stall right, stall left, and left respectively. Define

,

where. In the Fourier domain the amplitude of the wave function takes the form

, where is the Fourier transform of. Let

be the initial state of the system in the Fourier picture, then the evolution of the 2cQW is given by

,

where is the unitary operator in the governing the quantum walk. We should remark that, where is the coin operator in the single-coin framework.

Now consider the “2cQW” where the unitary matrix governing the walk is given by it is an open question what is the limiting distribution of the “2cQW” determined by.

Consider the discrete-time nearest-neighbor quantum walk in a random environment (QWRE) on the line, whose evolution proceeds almost everywhere as in the case of the inhomogeneous quantum walk. The definition of the QWRE can be made more precise as follows: Let, where is the set of real numbers. A random environment is an -valued random variable with probability measure. Assume that is a product measure on, where is the Borel of, then we can write

,

where is a probability measure on, and is the Borel of. Suppose is a parametrization of the matrix

,

that is, let, where is the diagonal phase adjustments with. Suppose that is independent identically distributed, that is, does not depend on. When, the walk is non-random and position independent. In particular we see that

,

and thus. We should remark that is the operator governing the parametrized Grover walk in one dimension. When the quantum walk is conditioned upon the environment, the QWRE is said to be quenched. On the other hand averaging over the environment, the QWRE is said to be annealed. In [78] weak limit theorems for both the quenched and annealed QWRE are presented for a Hadamard- type operator governing the quantum walk on a random environment by counting the number of paths that it takes a quantum walker from the origin to a position. It is an open question what is the weak limit theorems for

both the quenched and annealed QWRE for the Grover-type operator.

8.5. Inhomogeneous Quantum Walk

Consider the discussion of the inhomogeneous quantum walk in this paper. Suppose, is a given sequence. Let

.

For, define, if. If, the walk is homogeneous except the origin. If, the walk is homogeneous and is equivalent to the Grover transformation on the line,

.

We clearly see, thus the distribution of the walk cannot be described by the Konno density function.

It is an open question what is the limiting distribution of the inhomogeneous walk, or the homogeneous walk. Since the Grover walk is an example of quantum diffusion,

it is interesting to have an asymptotic probability function that captures this phenomenon. The result will be significant for quantum information processing task.

Cite this paper

Clement Ampadu, (2014) On Some Questions of C. Ampadu Associated with the Quantum Random Walk. Applied Mathematics,05,3040-3066. doi: 10.4236/am.2014.519291

References