Applied Mathematics
Vol. 4 No. 10 (2013) , Article ID: 37857 , 5 pages DOI:10.4236/am.2013.410198
Theoretical Study of Electromagnetic Wave Propagation: Gaussian Bean Method
Department of Industrial Physics, Ebonyi State University, Abakaliki, Nigeria
Email: ugwuei@hahoo.com
Copyright © 2013 E. I. Ugwu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 21, 2013; revised April 21, 2013; accepted April 29, 2013
Keywords: Electromagnetic Wave; Wave Equation; Dielectric Medium; Distribution; Gaussian Function; Intensity; Electric Field; Beam Waist; Wave Propagation
ABSTRACT
In this work, we present the study of electromagnetic wave propagation through a medium with a variable dielectric function using the concept of Gaussian Beam. First of all, we start with wave equation 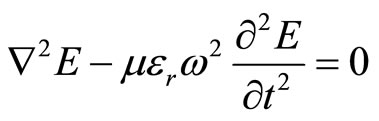 with which we obtain the solution in terms of the electric field and intensity distributions approximate to Gaussian Function,
with which we obtain the solution in terms of the electric field and intensity distributions approximate to Gaussian Function,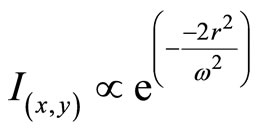 . With this, we analyze the dependency of r on Gaussian beam distribution spread, the distant from the axis at which the intensity of the beam distribution begins to fall at a given estimate
. With this, we analyze the dependency of r on Gaussian beam distribution spread, the distant from the axis at which the intensity of the beam distribution begins to fall at a given estimate  of its peak value. The influence of the optimum beam waist wo and the beam spread on the intensity distribution will also be analyzed.
of its peak value. The influence of the optimum beam waist wo and the beam spread on the intensity distribution will also be analyzed.
1. Introduction
Along with the rapid evolution of fiber optics, integrated optics and application of laser in both medicine and technology, there has been a growing interest in the study of Gaussian beam propagation. This is based on the fact that Gaussian beam has to do with focusing and modification of shape of propagating electromagnetic wave or laser beam. From the earlier finding on the research on laser beam, it has been found that laser beam propagation can be approximated by an ideal Gaussian beam intensity profile [1,2]. Understanding of the basic properties of Gaussian beam has been specifically found to be very vital. I select the best optics for practical application [3]. Sequel to this, lots of scientists had worked on Gaussian beam applications in electromagnetic wave propagation and in optics. For instance, a work has been carried out on nonspecular phenomena for beam reflection at monolayer and multilayered dielectric interface respectively from where it has revealed that under various conditions nonspecular beam phenomena is more realizable [4-6]. Tamir on his own presented a unified and simplified analysis of the lateral and longitudinal displacement with angular deflection on reflection of a Gaussian beam at a dielectric interface with two or more layer [7,8].
However in this paper, we intend to study electromagnetic wave propagation using the concept of Gaussian beam starting from general wave equation with which obtain the Gaussian function in which waves operating on the fundamental transverse mode is approximated to Gaussian profile. The distribution profile is analyzed with intent to observe the influence of the beam waist on the profile.
2. Theoretical Framework
In this case we start with wave equation in terms of electric field given as
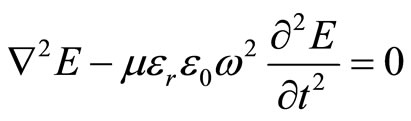 (1)
(1)
where 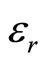 is the dielectric constant as a function wave solution of the form
is the dielectric constant as a function wave solution of the form
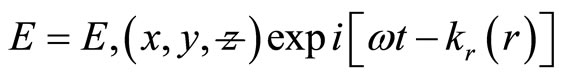 (2)
(2)
Which if we consider medium with non-uniform refractive index, we have
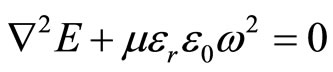 (3)
(3)
where the propagation constant in the medium is given by
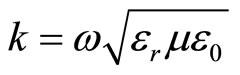 (4)
(4)
With this, Equation (2) becomes
 (5)
(5)
In general, if the medium is absorbing or exhibit gain, the its dielectric constant 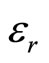 is considered to have real and imaginary part, but in a situation where the medium conducts with conductivity
is considered to have real and imaginary part, but in a situation where the medium conducts with conductivity 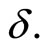 then the complex propagation vector is introduce which obeys.
then the complex propagation vector is introduce which obeys.
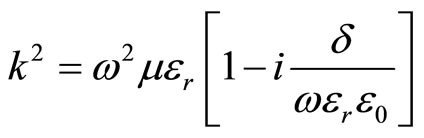 [9]. (6)
[9]. (6)
However, a simple solution of this type is inadequate to describe the field distributions of transverse mode. As a result, we seek solution to the plane wave equation of the form.
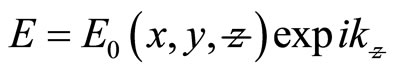 (7)
(7)
Propagating in the z-direction and localized the z-axis. Thus the idea is to obtain a solution of the wave equation that gives phase front that can be approximated over a narrow region. Thus substituting Equation (7) into Equation (4) we obtain.
 (8)
(8)
Since we are looking for a paraxial beam-like solution, then 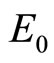 varies slowly with
varies slowly with  and Equation (8) becomes
and Equation (8) becomes
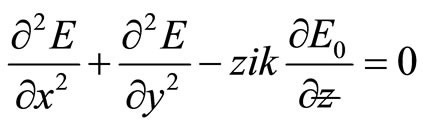 (9)
(9)
With a solution given as
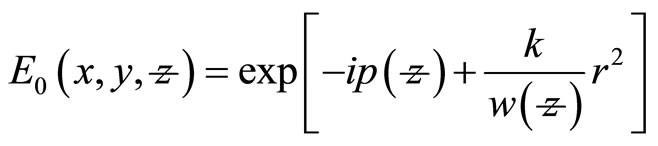 (10)
(10)
where  is the square distant of the points x, y from the axis of propagation where
is the square distant of the points x, y from the axis of propagation where 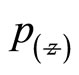 and
and 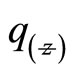 are beam parameters Equation (10) gives the fundamental Gaussian beam of time-independent wave equation.
are beam parameters Equation (10) gives the fundamental Gaussian beam of time-independent wave equation.
3. Intensity of Gaussian Beam
The intensity of 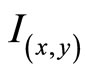 of Gaussian beam is given by
of Gaussian beam is given by
 (11)
(11)
where 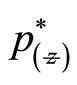 and
and  are the complex conjugate of
are the complex conjugate of 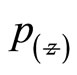 and
and 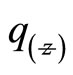 respectively hence
respectively hence
 (12)
(12)
Considering two real beam parameters that  and
and ![]() relating to
relating to 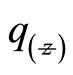 by depend on
by depend on 
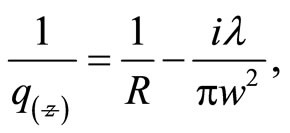 (13)
(13)
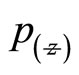 is that describes the axial distance from the Gaussian beam waist.
is that describes the axial distance from the Gaussian beam waist.
We can express Equation (11) as
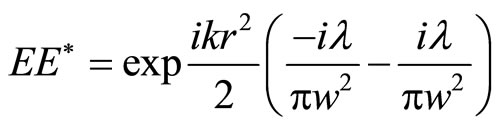 (14)
(14)
 (15)
(15)
Signifying the dependency of Gaussian beam intensity to r while w signifies the distance from the axis at 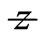
where the intensity of the beam falls to  of it its peak value on the axis
of it its peak value on the axis 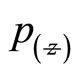 total power of the beam with these parameters Equation (10) is now written as
total power of the beam with these parameters Equation (10) is now written as
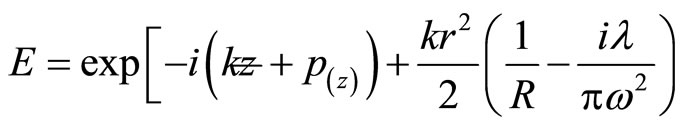 (16)
(16)
 is evaluate to give
is evaluate to give
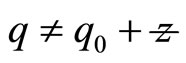 (17)
(17)
where 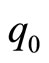 is a constant of integration the expresses the value of the beam parameter at the plane
is a constant of integration the expresses the value of the beam parameter at the plane 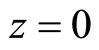 for which when we consider
for which when we consider 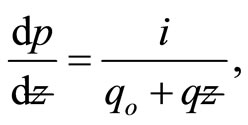 we obtain
we obtain
![]() (18)
(18)
where 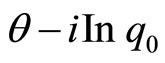 defines a constant of integration substituting Equation (18) into (16) we have
defines a constant of integration substituting Equation (18) into (16) we have
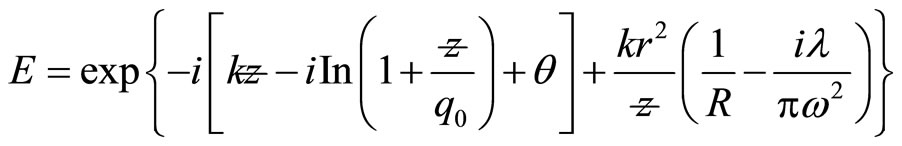 (19)
(19)
The factor 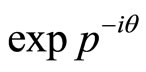 is a constant phase factor. Thus
is a constant phase factor. Thus
 (20)
(20)
4. Diffraction Effect
The limitations of Gaussian beam based on the fact that even if the wave fronts were made flat at some plane, it quickly acquires curvature and begin to spread in accordance with
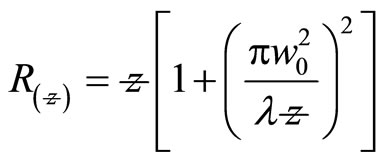 (21)
(21)
and
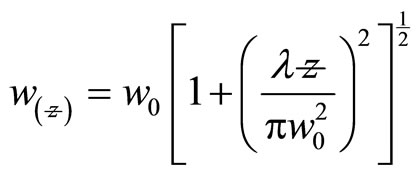 (22)
(22)
where 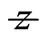 is the distance propagated from the plane where the wave-front is flat
is the distance propagated from the plane where the wave-front is flat  wavelength of light,
wavelength of light,
 is the radius of the
is the radius of the 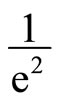 irradiance contour at the plane where wave-front is flat,
irradiance contour at the plane where wave-front is flat, 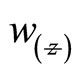 is the radius of the
is the radius of the
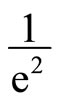 contour after the wave has propagated a distance
contour after the wave has propagated a distance
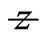 .
.
Considering the optimum starting beam radius for a distance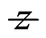 , we have
, we have  Equation (22) can be reduced to
Equation (22) can be reduced to
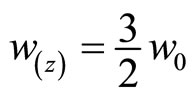 (23)
(23)
With the irradiance distance distribution of the Gaussian beam described as
 (24)
(24)
where 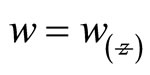 and
and  is the total power in the beam which is the same at all cross sections of the beams we also obtain that
is the total power in the beam which is the same at all cross sections of the beams we also obtain that
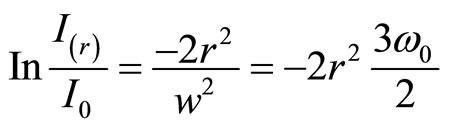 (25)
(25)
 (26)
(26)
at optimism starting beam radius for a given distance, .
.
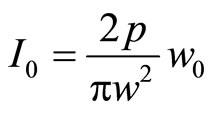 (27)
(27)
5. Discussion
From the displayed results in Figure 1, the distribution profile when y = 2, x = 2 and w = 2, the distribution beam width ranged within −5 to 5, In Figure 2, for y = 2 and x = 3 when w = 2, the width of the beam ranged from −6.5 to 6.5. In Figures 3 and 4 the distribution profiles displayed is found to be departed from normal distribution shape as in the other figures when w is increased to 5 for

Figure 1. Gaussian distribution profile when y = 2, w = 3.

Figure 2. Gaussian distribution profile when y = 2, w = 4.
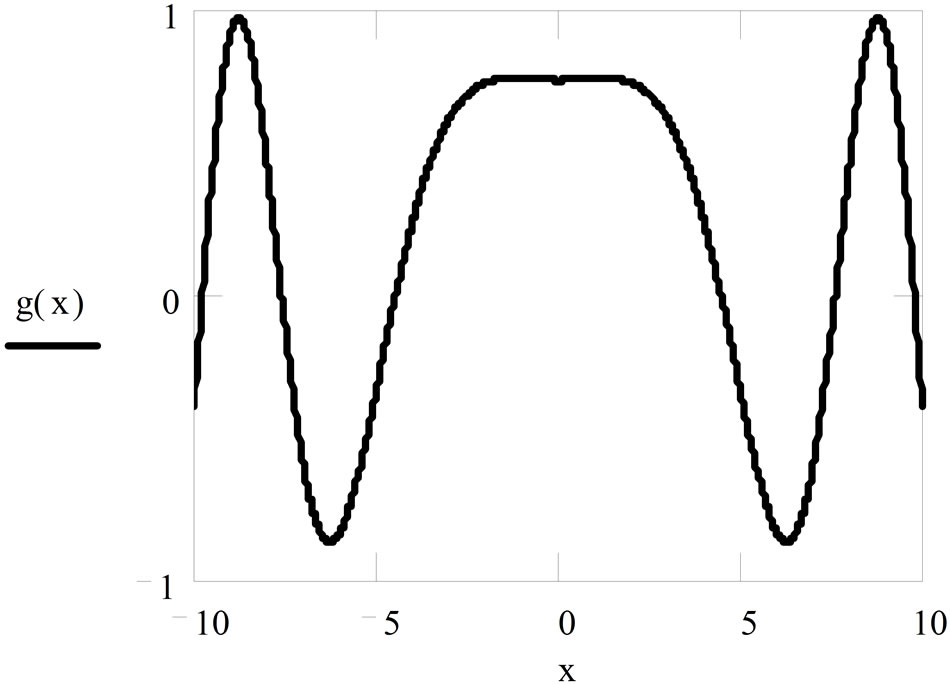
Figure 3. Gaussian distribution profile when y = 2, w = 5.
y = 2 when w = 10, the departure became more pronounced pattern as shown in Figure 5. However, the distribution profile of percentage irradiance as function

Figure 4. Gaussian distribution profile when y = 2, w = 5.
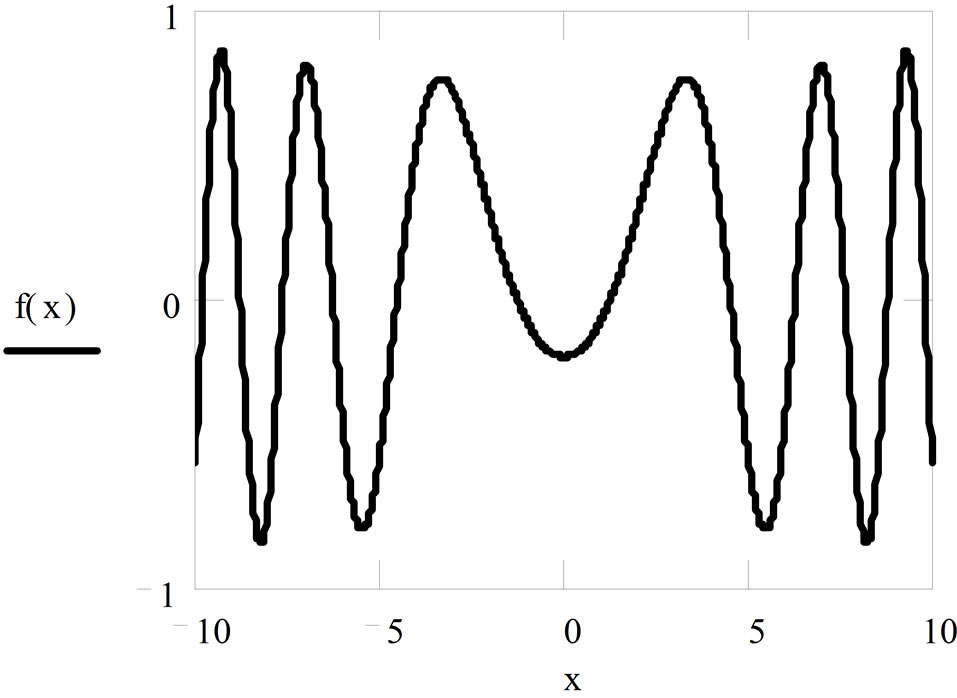
Figure 5. Gaussian distribution profile when λ = 0.50 mm, y = 2, w = 10.
contour radius as displayed in Figure 6 indicate the fact that as the contour decreases, the beam distribution tappers showing that there is a point known as spot size where the intensity of the distribution is fallen to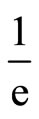 .
.
This indicates that Gaussian distribution function depends on r as shown in Equation (16) that depicts characteristic of normal distribution function.
However, the shape of the distribution depends generally on diameter at which the intensity has fallen of 
as in Figure 7 when x = y coupled with the optimum beam waist that is given as axial distance and Raleigh range which is given in Equation (22) with
axial distance and Raleigh range which is given in Equation (22) with 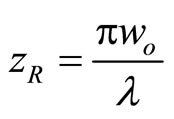 [9] These values provide the best combination for minimum starting beam diameter for good minimum spread according to [10] whose ratio is
[9] These values provide the best combination for minimum starting beam diameter for good minimum spread according to [10] whose ratio is  over a distant z and a particular wavelength.
over a distant z and a particular wavelength.
6. Conclusions
Gaussian intensity profiles as observed from this study seem to manifest one feature that is based on the fact that beam waist, w plays a role in determining the distribution profile. This explains the fact that the far-field divergence
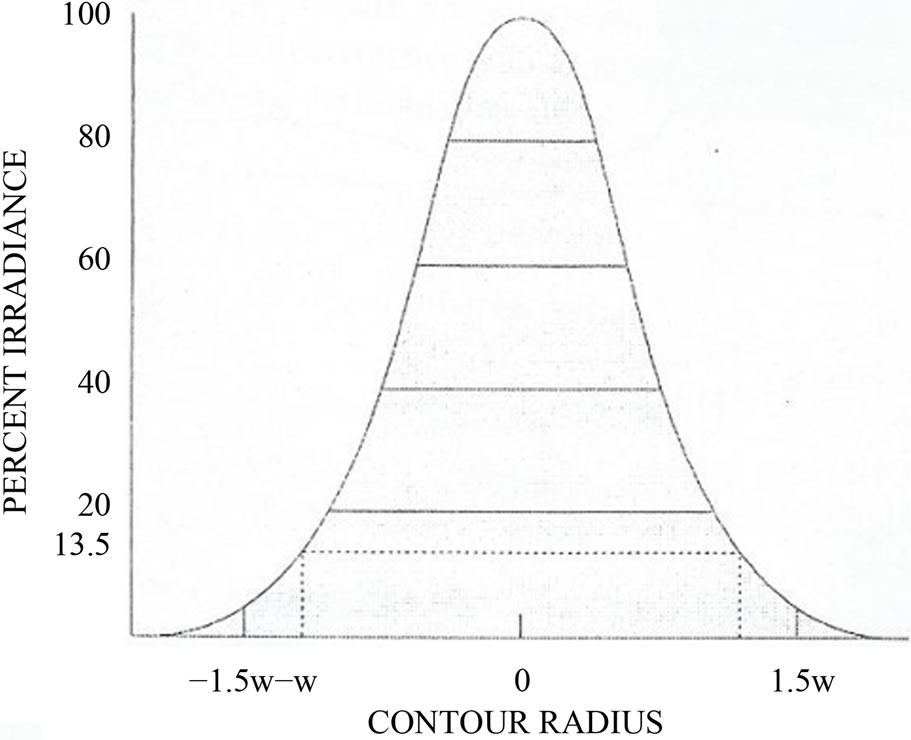
Figure 6. Percentage irradiance.
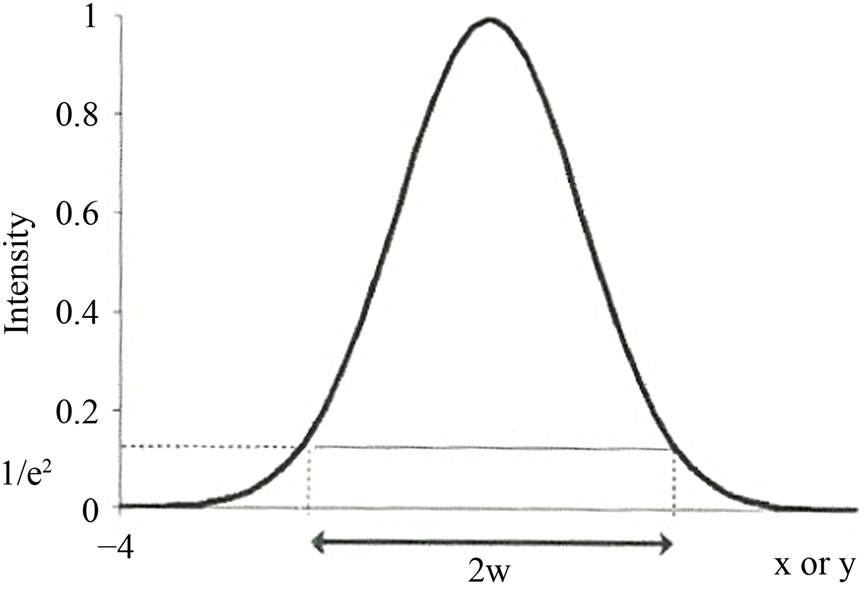
Figure 7. Gaussian distribution intensity as function of profile width, w.

Figure 8. Gaussian beam width w(z) as a function of the axial distance z.
must be measured at a distance greater than the half width of intensity distribution while the near or mid-field divergence values are obtained by measuring a distance less than the half width of the intensity distribution in order to obtain a good normal distribution profile. Therefore in order to achieve optimum beam spread, and collimation over a distance, the optimum starting beam radium/waist must be determined. Though one should note that this depends strictly on the type of beam that is whether the beam is coherent or not, the general expression for optimum starting beam radius for any given distance,  is
is

This study also reveals that the concept of Gaussian beam is realizable when it is focused on a small spot as it spreads out rapidly as it propagate away from the spot From Figures 3 to 6, it is clearly shown that at certain value of the beam waist, the distribution profile changes. Therefore for a beam to be well collimated, it must have a large diameter. This relation is as a result of diffraction. Thus in order to achieve normal Gaussian beam distribution, the product of the width and divergence of the beam profile must be as small as possible to be achieved when paraxial approximation is considered. Thus this implies that the idea of Gaussian beam model is realizable and valid only for beam whose width is larger than that of equation.
REFERENCES
- A. Siegman, “Lasers Sensitization,” C.A University Sciences Books, 1986.
- S. A. Self, “Focusing of Spherical Gaussian Beam,” Applied Optics, Vol. 22, No. 5, 1983, pp. 658-661.
- H. Sun, “Thin Lens Equation for a Real Laser Beam with Weak Lens Aperture Truncation,” Optical Engineering, Vol. 37, No. 11, 1998, pp. 2903-2913. http://dx.doi.org/10.1117/1.601877
- J. W. Ra, H. L. Bertoni and L. B. Felsen, “Reflection and Transmission of Beam at Dielectric Interface,” SIAM Journal on Applied Mathematics, Vol. 24, No. 3, 1973, pp. 396-413.
- M. McGuirik and C. K. Carniglia, “An Angular Spectrum Representation Approach to the Goos-Hänchen Shift,” Journal of the Optical Society of America, Vol. 67, No. 1, 1977, pp. 103-107. http://dx.doi.org/10.1364/JOSA.67.000103
- R. P. Riesz and R. Simon, “Reflection of a Gaussian Beam from a Dielectric Slab,” Journal of the Optical Society of America A, Vol. 2, No. 11, 1985, pp. 558-565.
- T. Tamir, “Nonspecular Phenomena in Beam Field Reflected by Multilayered Media,” Journal of the Optical Society of America A, Vol. 3, No. 4, 1986, pp. 586-594.
- S. Z. Zhang and C. C. Fan, “Nonspecilar Phenomena on Gaussian Beam Reflection at Dielectric Interface,” Journal of the Optical Society of America A, Vol. 5, No. 9, 1988, pp. 1407-1411. http://dx.doi.org/10.1364/JOSAA.5.001407
- F. Pampaloni and J. Enderlein, “Gaussian, HermiteGaussian, and Laguerre Gaussian Beam: A Primer,” 2004, 29p.
- J. Ralton, “Gaussian Beams and the Propagation of Singularity, Studies in Partial Differential Equations,” MAA Studies in Mathematics, Vol. 23, 1982, pp. 206-248.

