Applied Mathematics
Vol. 4 No. 5 (2013) , Article ID: 31571 , 6 pages DOI:10.4236/am.2013.45116
On the Frame Properties of System of Exponents with Piecewise Continuous Phase
1Institute of Mathematics and Mechanics of NASA, Baku, Azerbaijan
2Nakhchivan State University, Nakhchivan, Azerbaijan
Email: saeedzfarahani@gmail.com, tofiq-necefov@mail.ru
Copyright © 2013 Saeed Mohammadali Farahani, Tofig Isa Najafov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 14, 2013; revised April 3, 2013; accepted April 10, 2013
Keywords: System of Exponents; Frame Property; Perturbation
ABSTRACT
A double system of exponents with piecewise continuous complex-valued coefficients are considered. Under definite conditions on the coefficients the frame property of this system in Lebesgue spaces of functions is investigated. Such systems arise in the spectral problems for discontinuous differential operators.
1. Introduction
Consider the following system of exponents
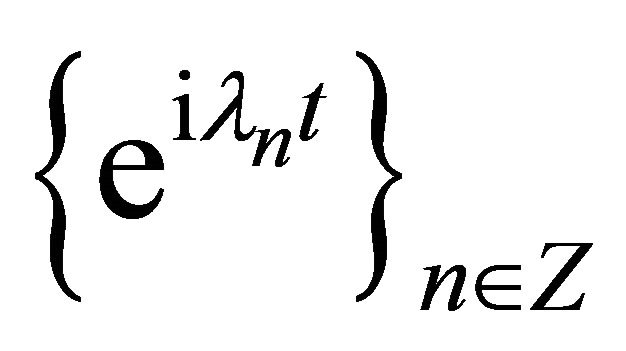 , (1)
, (1)
where 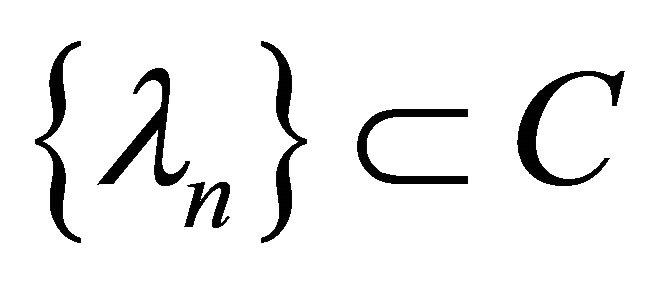 is a sequence of complex numbers, Z are integers. Systems (1) are model ones while studying spectral properties of differential operators. Under suitable choice of the bounded variation function
is a sequence of complex numbers, Z are integers. Systems (1) are model ones while studying spectral properties of differential operators. Under suitable choice of the bounded variation function 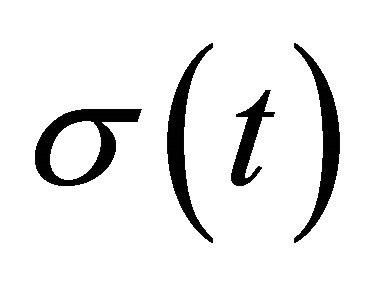 on the segment
on the segment 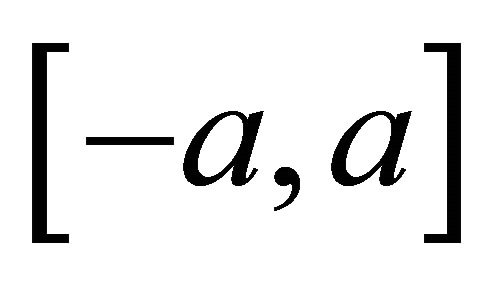 they are eigenfunctions of first order differential operator
they are eigenfunctions of first order differential operator 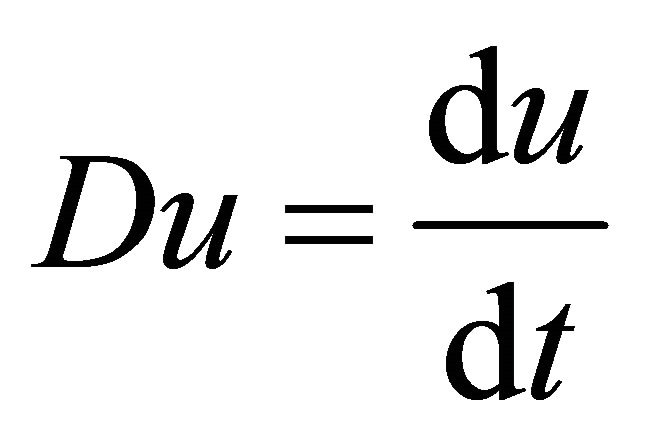 with an integral condition of the form
with an integral condition of the form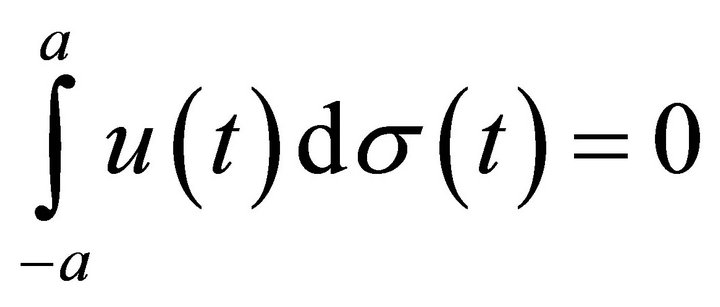 .
.
For this reason, many mathematicians appealed to study of basis properties of the systems form (1) in different spaces of functions. If the operator D is considered in the Lebesgue space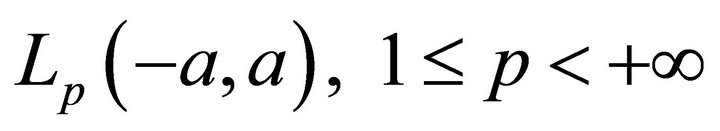 , then its natural domain of definition is the Sobolev space
, then its natural domain of definition is the Sobolev space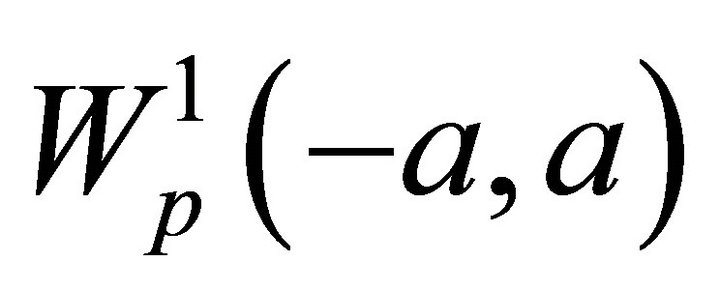 , i.e. the space consisting of absolutely continuous on
, i.e. the space consisting of absolutely continuous on 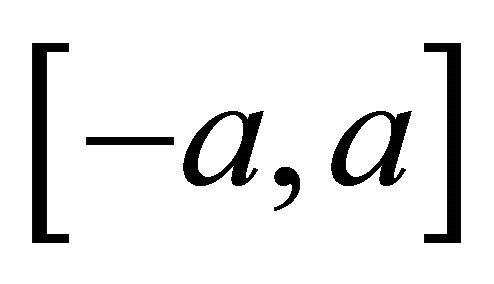 functions, whose derivatives belong to
functions, whose derivatives belong to 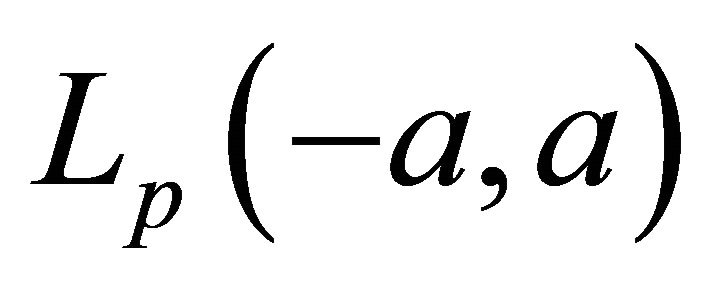 and the relation
and the relation
 , (2)
, (2)
holds a.e. on all the segment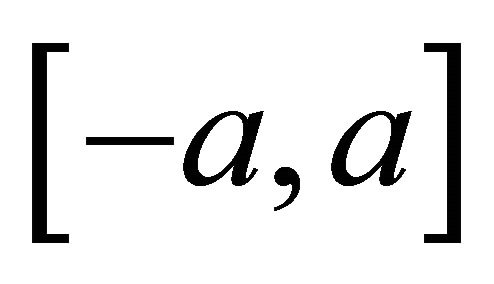 .
.
Apparently, the first results for basis properties of the systems of the form (1) in the spaces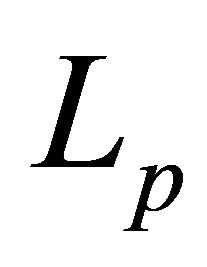 ,
,  ,
, 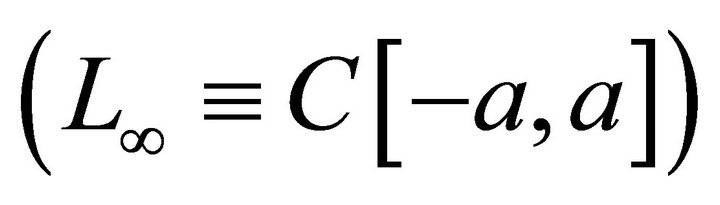 belong to the famous mathematicians Paley P.-N. Wiener [1] and N. Levinson [2]. In sequel, this direction was developed in the investigations of many mathematicians. For more detailed information see the monographs of R. Young [3], A. M. Sedletskii [4], Ch. Heil [5], O. Christensen [6] (and also the papers [7- 9]) and their references. There is also the survey paper [10].
belong to the famous mathematicians Paley P.-N. Wiener [1] and N. Levinson [2]. In sequel, this direction was developed in the investigations of many mathematicians. For more detailed information see the monographs of R. Young [3], A. M. Sedletskii [4], Ch. Heil [5], O. Christensen [6] (and also the papers [7- 9]) and their references. There is also the survey paper [10].
Many problems of mechanics and mathematical physics reduce to discontinuous differential operators, i.e. to the case when the domain of definition of a differential operator is not connected. It should be noted that the systems of the form
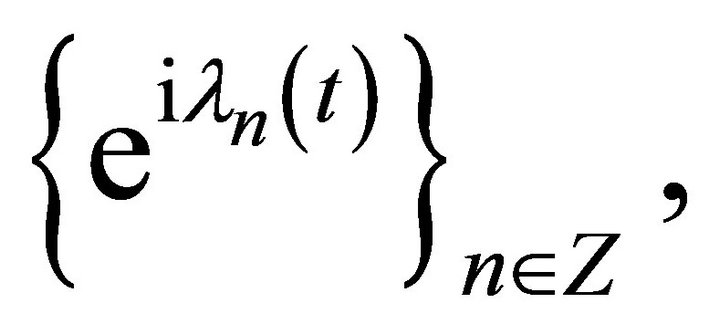 (3)
(3)
where 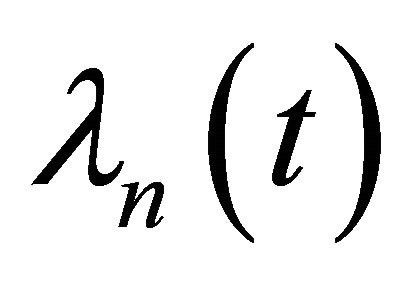 has the representation
has the representation
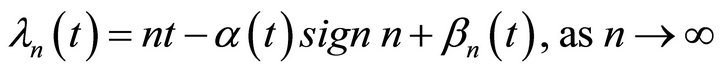 . (4)
. (4)
arise as eigen functions of appropriate differential operators while solving many problems of mechanics and mathematical physics by the method of separation of variables. The following system is a trivial example of the case under consideration
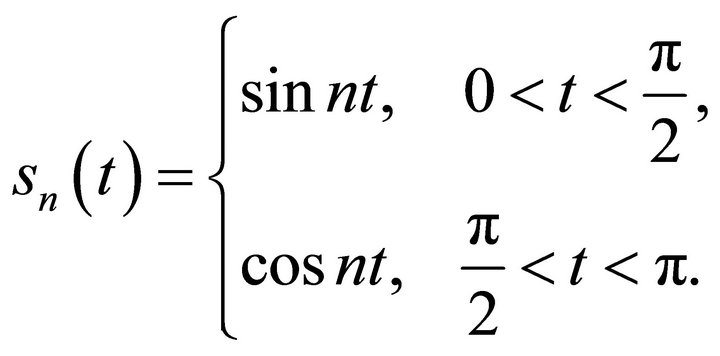
Let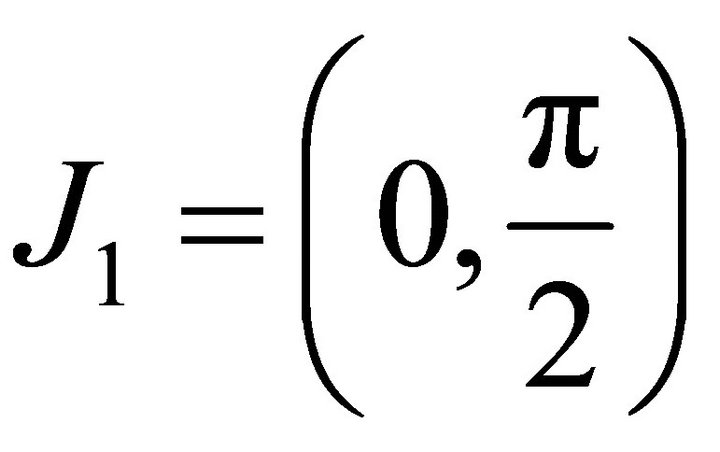 ,
, . It is obvious that
. It is obvious that 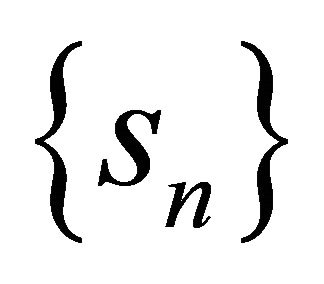
are the eigen functions of the following spectral problem with a spectrum in boundary conditions

Concerning these issues see also the papers [11-14].
Another remarkable example is considered in V. A. Ilin’s paper [15]. Here he considers a mixed problem with conjugation conditions at the inner point  with respect to the wave equation
with respect to the wave equation
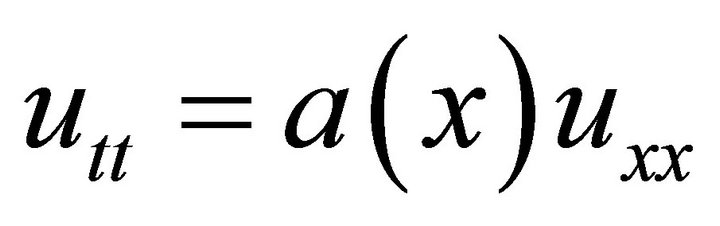 ,
, 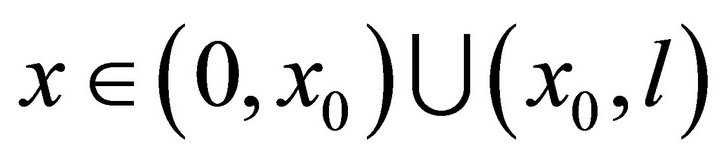 ,
,  with conditions
with conditions
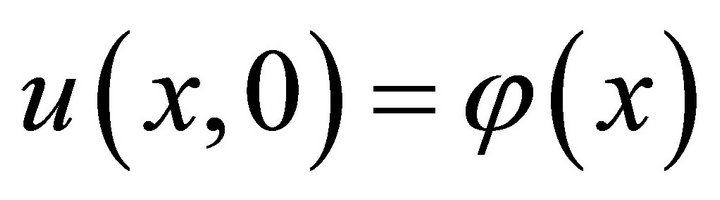 ,
, 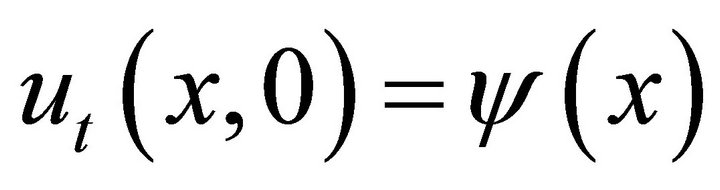 ,
, 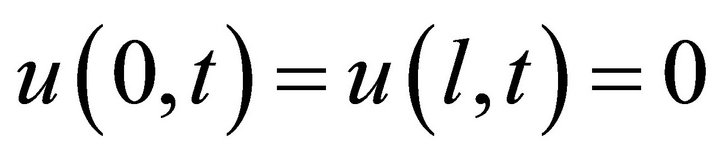 ,
, 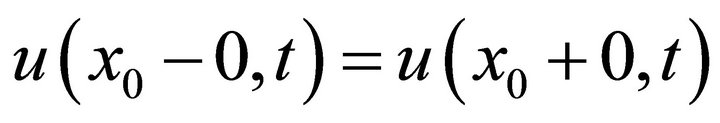 ,
, 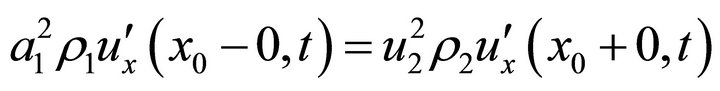 where
where
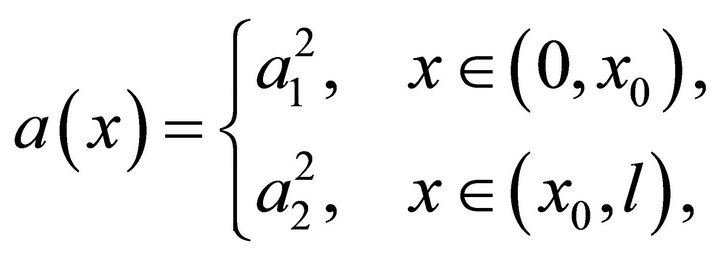
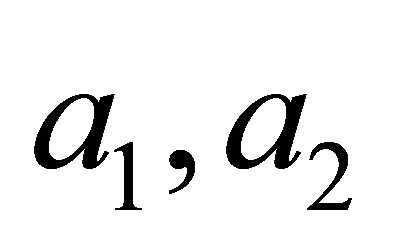 (wave velocity in medium) and
(wave velocity in medium) and  (medium density) are positive constants,
(medium density) are positive constants, 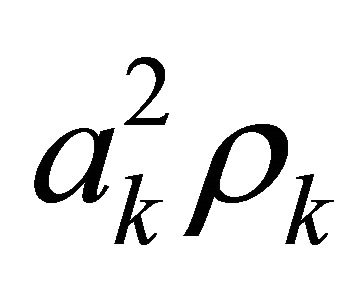 are Young modules with additional condition of equality of passage time of wave the segments
are Young modules with additional condition of equality of passage time of wave the segments 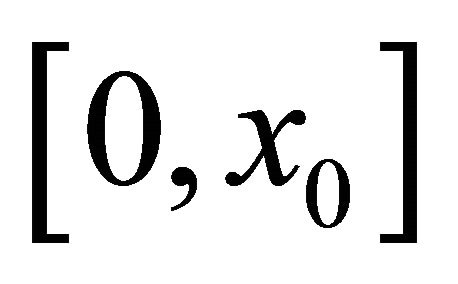 and
and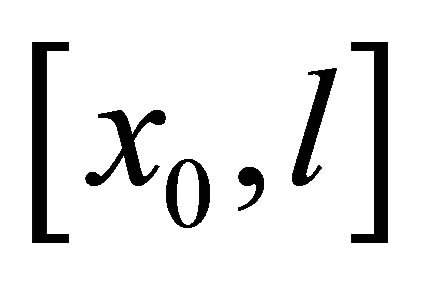 :
: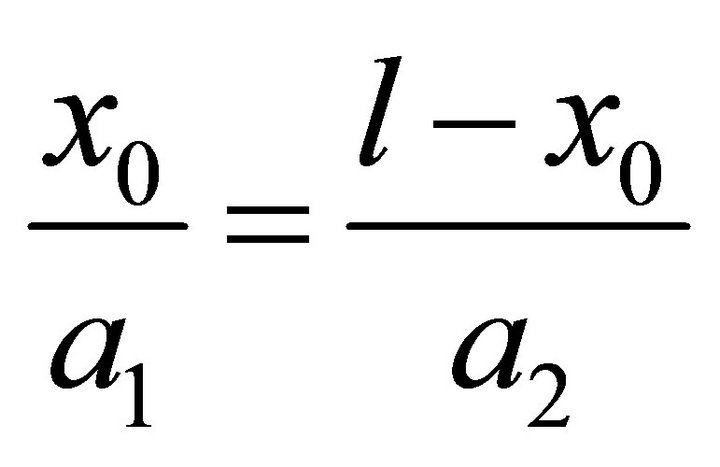 .
.
The completeness in 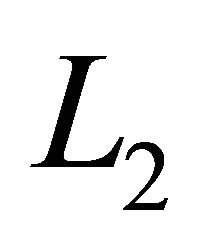 of the system of eigenfunctions of an ordinary differential operator that corresponds to this problem is established in the paper [16]. The close class of problems was earlier considered in the paper [17].
of the system of eigenfunctions of an ordinary differential operator that corresponds to this problem is established in the paper [16]. The close class of problems was earlier considered in the paper [17].
These examples very clearly demonstrate expediency of study of frame properties of the systems form (3). The present paper is devoted to investigation of frame property of system (3) in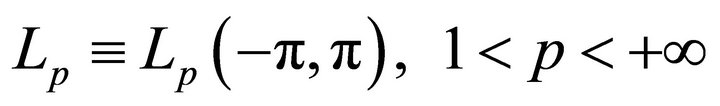 . Previously some results of this paper were announced without proof in [18].
. Previously some results of this paper were announced without proof in [18].
This work is structured as follows. In Section 2, we present needful information and facts from the theories of bases and close bases that will be used to obtain our main results. This section also contains the main assumptions about the functions 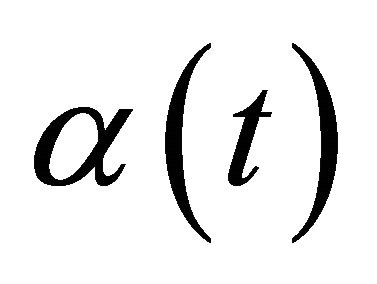 and
and 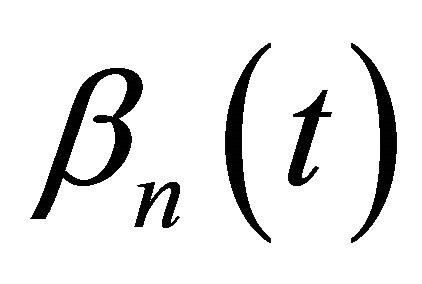 which appear in formula (4). In Section 3, we state main results on the basicity of the perturbed system of exponents (3) in Lebesgue spaces
which appear in formula (4). In Section 3, we state main results on the basicity of the perturbed system of exponents (3) in Lebesgue spaces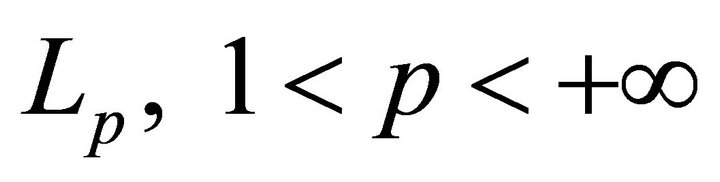 .
.
2. Necessary Information and Main Assumptions
In sequel we will need the following notion and facts from the theory of bases and frames. We will use the standard notation. N will be the set of all positive integers;  will mean “there exist(s)”;
will mean “there exist(s)”;  will mean “it follows”;
will mean “it follows”;  will mean “if and only if”;
will mean “if and only if”;  will mean “there exists unique”;
will mean “there exists unique”;  or
or 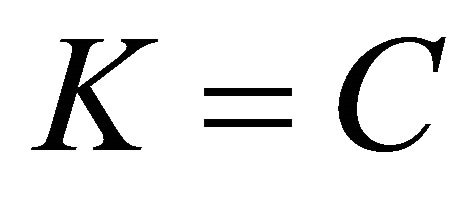 will stand for the set of real or complex numbers, respectively;
will stand for the set of real or complex numbers, respectively; 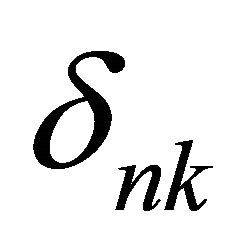 is Kroneckers symbol,
is Kroneckers symbol,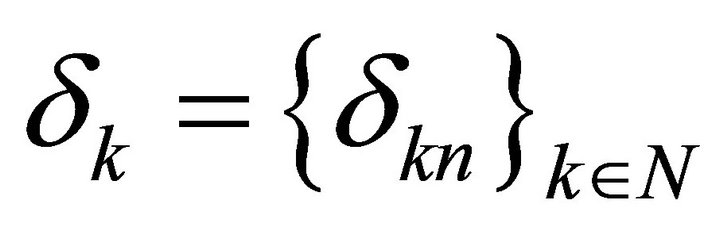 . The Banach space will be called a B-space.
. The Banach space will be called a B-space. 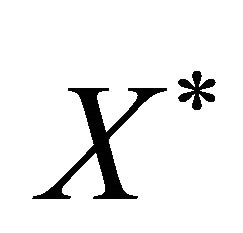 is a space conjugate to space X. By
is a space conjugate to space X. By  we denote the linear span of the set
we denote the linear span of the set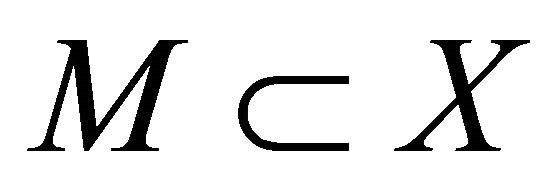 , and
, and 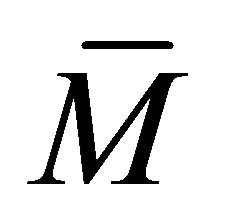 will stand for the closure of M.
will stand for the closure of M.
Definition 1. System  is said to be a basis for X if
is said to be a basis for X if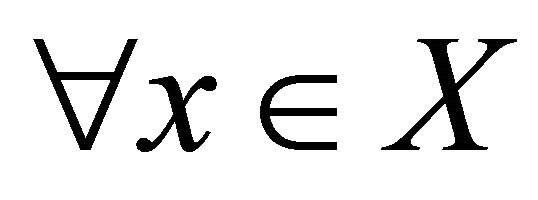 ,
, .
.
Definition 2. System 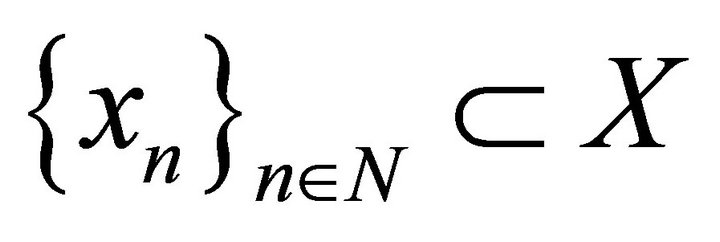 is said to be complete in X if
is said to be complete in X if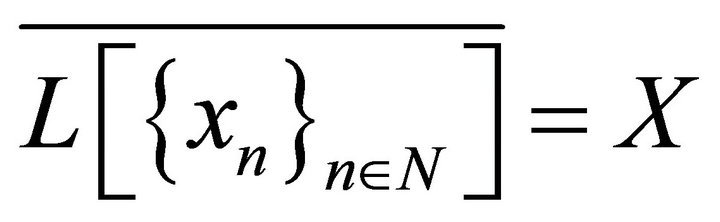 . It is called minimal in X if
. It is called minimal in X if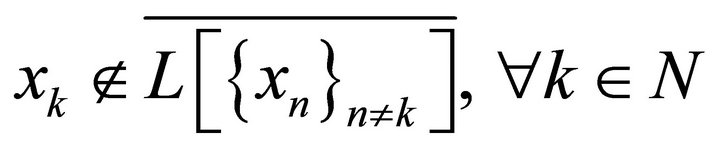 .
.
Definition 3. System 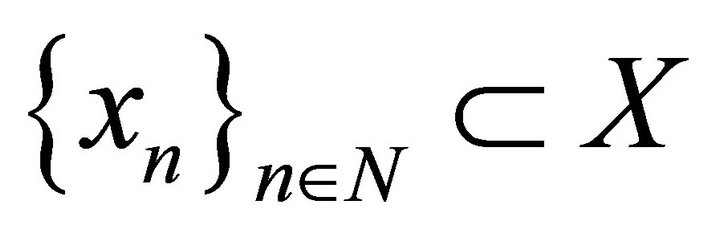 is called
is called  -linearly independent in
-linearly independent in  -space X, if from
-space X, if from 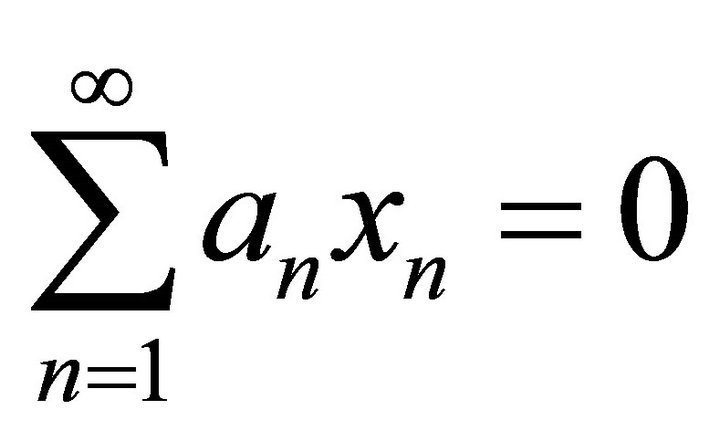 implies
implies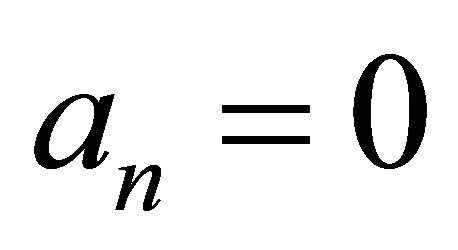 ,
,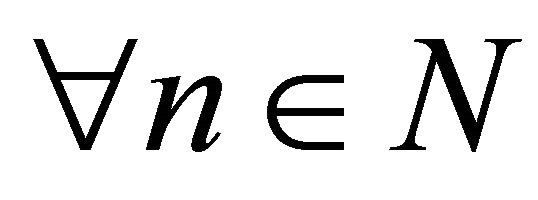 .
.
It holds the following Lemma 1. Let X be a B-space with the basis 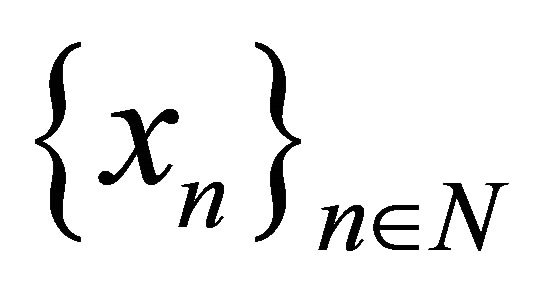 and
and 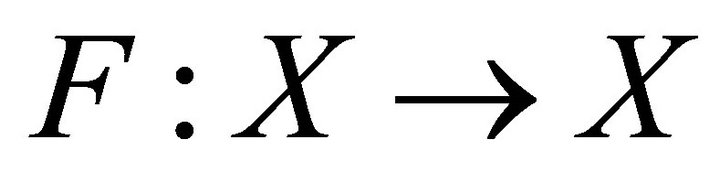 be a Fredholm operator. Then the following properties of the system
be a Fredholm operator. Then the following properties of the system  in X are equivalent:
in X are equivalent:
1)  is complete;
is complete;
2)  is minimal;
is minimal;
3) 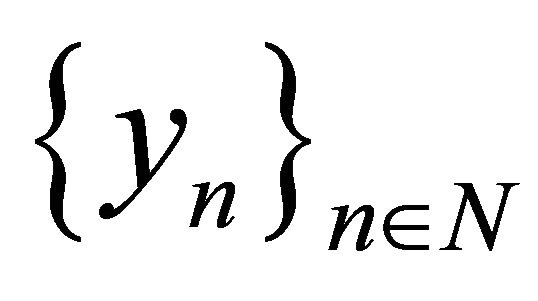 is
is  -linearly independent;
-linearly independent;
4)  a basis isomorphic to
a basis isomorphic to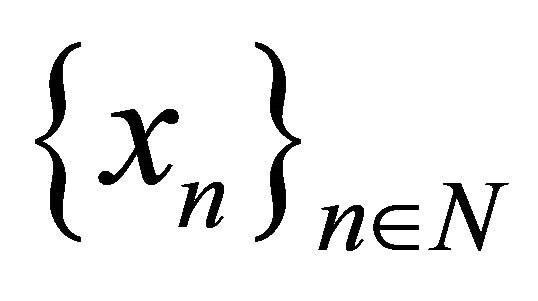 .
.
We will need the following notions.
Definition 4. The systems 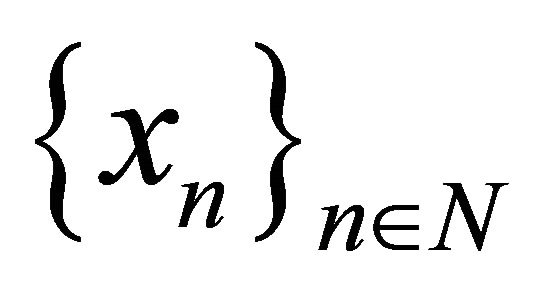 and
and 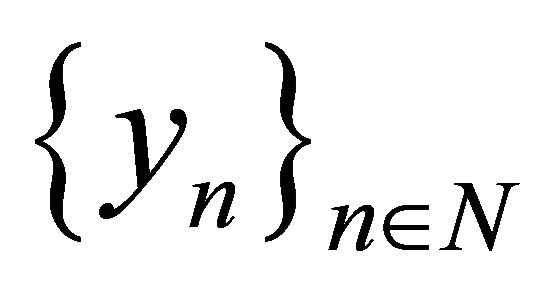 in a B-space X with the norm
in a B-space X with the norm 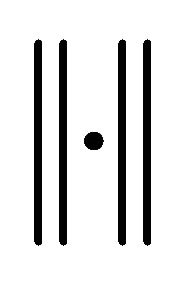 are said to be p-close, if
are said to be p-close, if
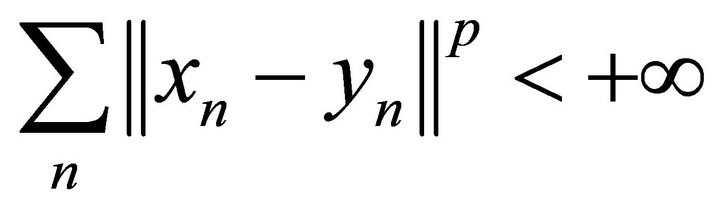 .
.
Definition 5. The minimal system 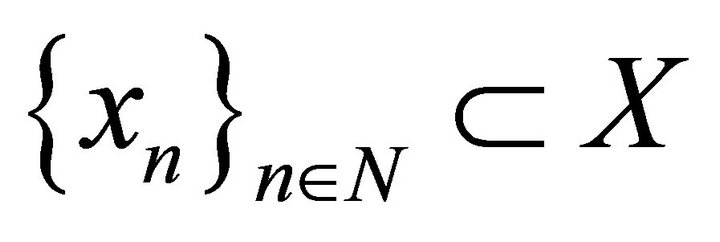 in a B-space X with conjugated
in a B-space X with conjugated  is said to be a p-system if for
is said to be a p-system if for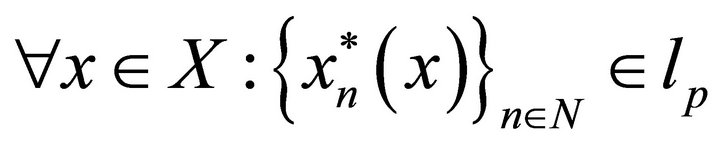 , where
, where 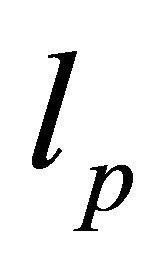 is an ordinary space of sequences
is an ordinary space of sequences 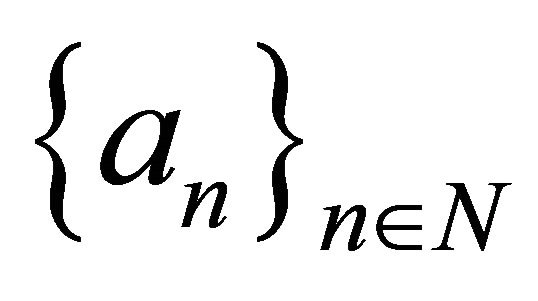 of scalars with the norm
of scalars with the norm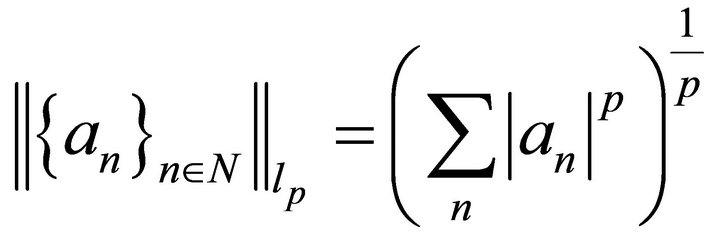 .
.
In the case of basicity, such a system will be called a p-basis.
The following lemma is also valid.
Lemma 2. Let X be a B-space with q-basis 
and the system 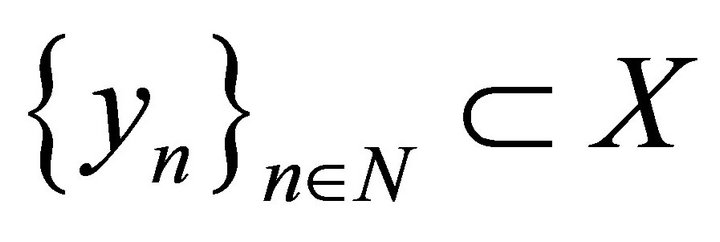 be p-close to it:
be p-close to it: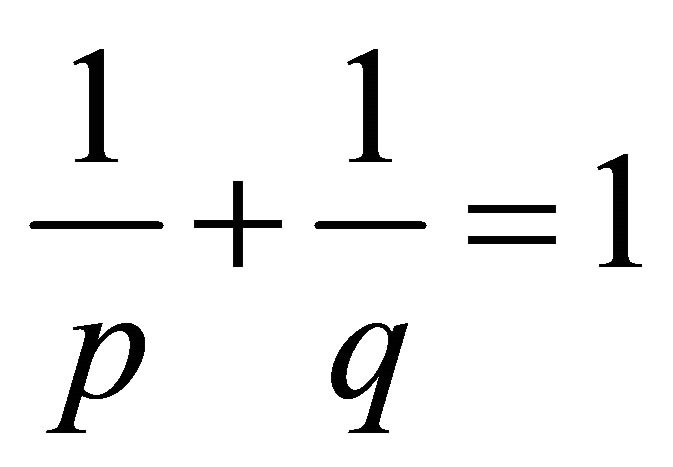 ,
,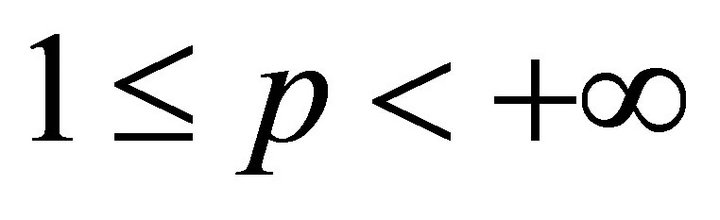 . Then the expression
. Then the expression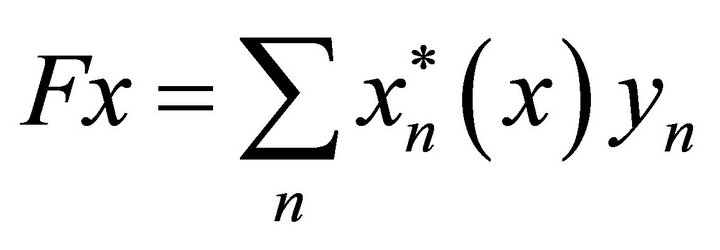 , generates a Fredholm operator in X, where
, generates a Fredholm operator in X, where  is a system conjugated to
is a system conjugated to .
.
One can see these or other facts in the monographs [3,19] and also in the papers [7,20-22]. We will need the following Krein-Milman-Rutman’s Theorem [20].
Theorem KMR. X be a B-space with the norm 
and with the normed basis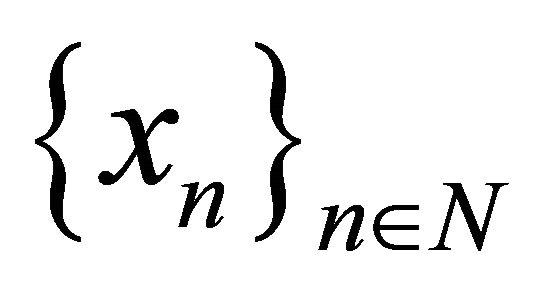 ,
, 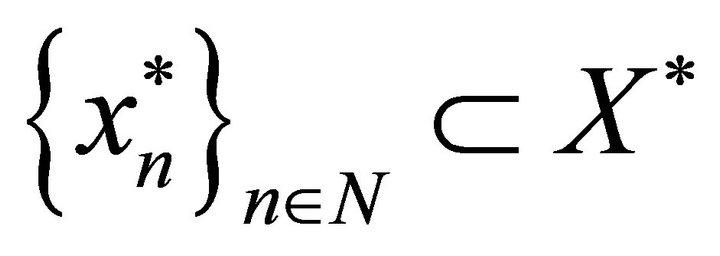 be a system biorthogonal to it. If the system
be a system biorthogonal to it. If the system 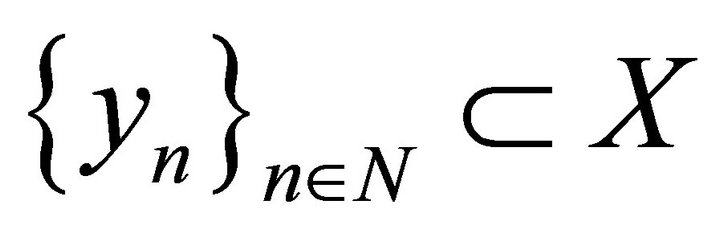
satisfies the condition , where
, where
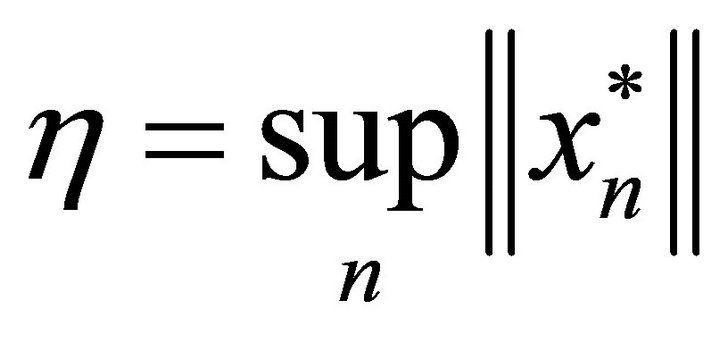 , then it forms a basis isomorphic to
, then it forms a basis isomorphic to 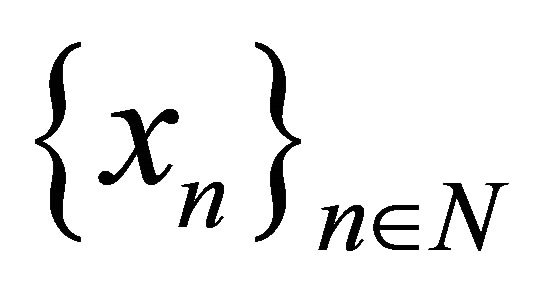 for X.
for X.
While obtaining the basic result, we will use the following easily provable lemma.
Lemma 3. Let X be a B-space with the basis  and
and 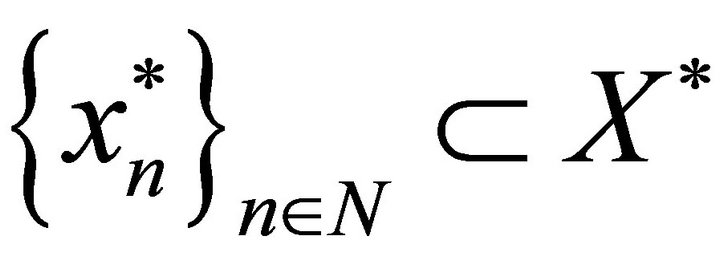 be a system biorthogonal to
be a system biorthogonal to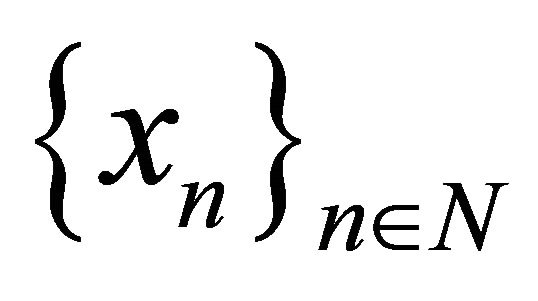 . The system
. The system  differ from
differ from 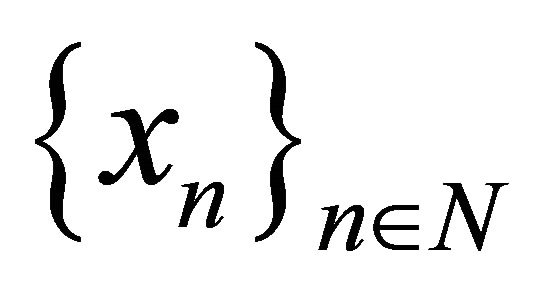 by a finitely many elements, i.e.
by a finitely many elements, i.e. ,
,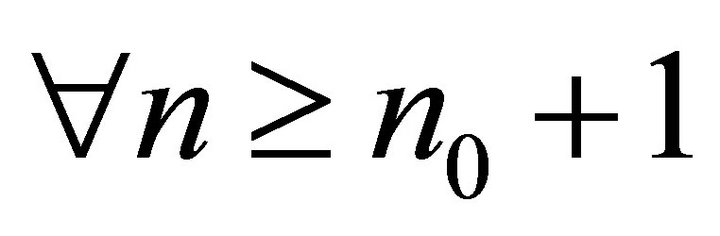 . Thenif
. Thenif  the system
the system  is not minimal in X.
is not minimal in X.
Proof. So, X be a B-space with the basis  and
and 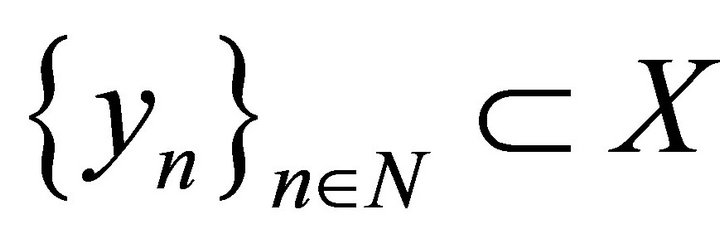 differ from
differ from  by finitely many elements, i.e.
by finitely many elements, i.e.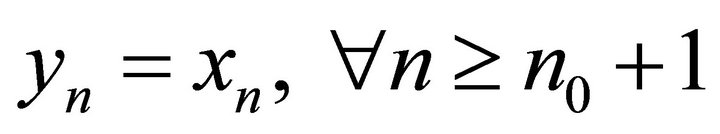 . Expand
. Expand . by this basis.
. by this basis.
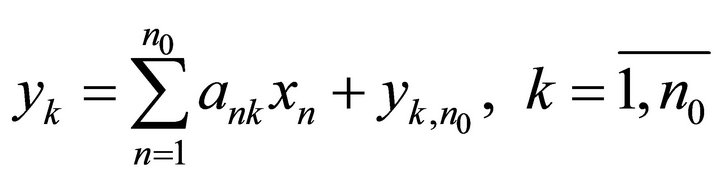 (5)
(5)
where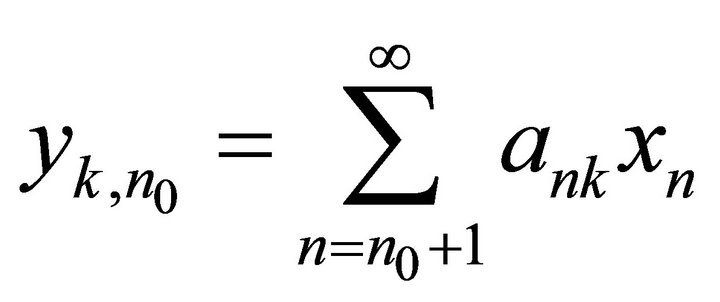 . Let
. Let . At first assume that
. At first assume that . Then, it is obvious that
. Then, it is obvious that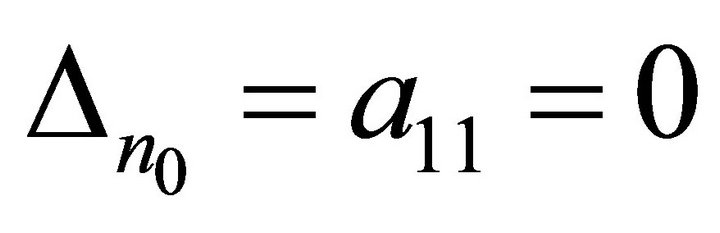 . As a result, it follows from expression (5) that
. As a result, it follows from expression (5) that 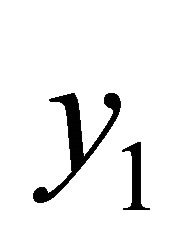 belongs to the closure of the linear span
belongs to the closure of the linear span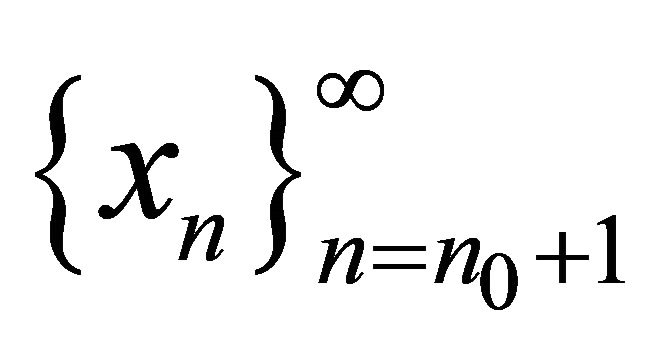 , and so the system
, and so the system 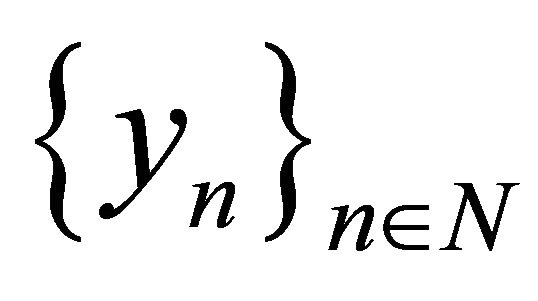 is not minimal. Consider the case
is not minimal. Consider the case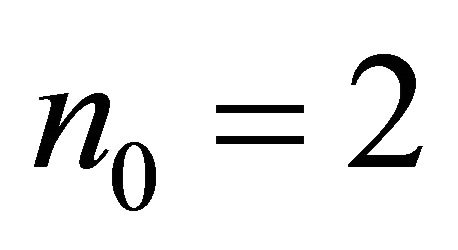 , i.e.
, i.e.
 (6)
(6)
where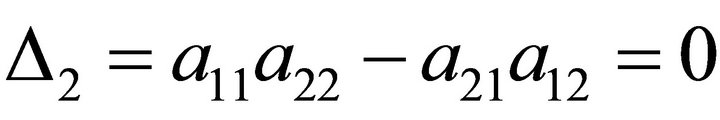 . It is obvious that if
. It is obvious that if 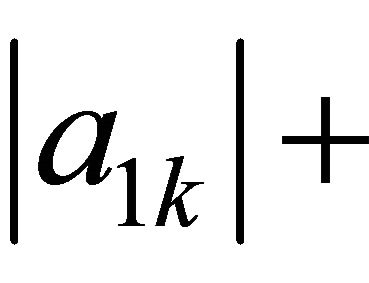
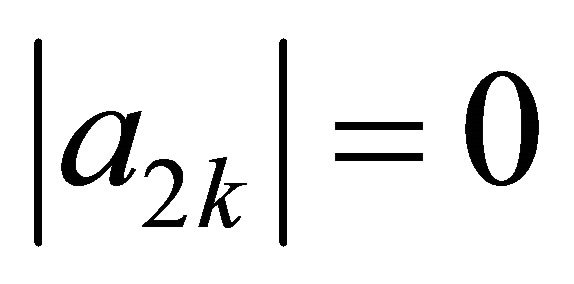 for
for 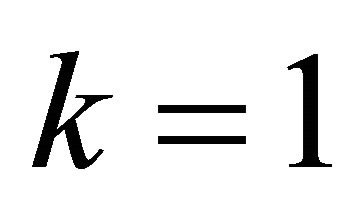 or
or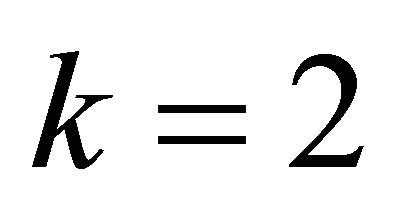 , then the system
, then the system 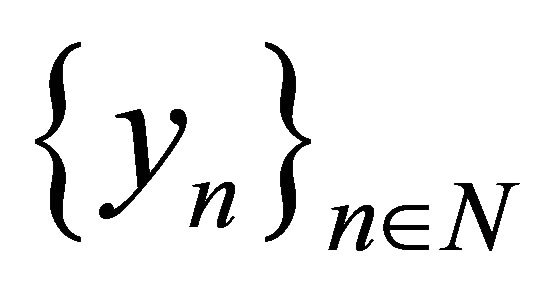 is not minimal. Otherwise, excluding xk in (6), we have:
is not minimal. Otherwise, excluding xk in (6), we have:
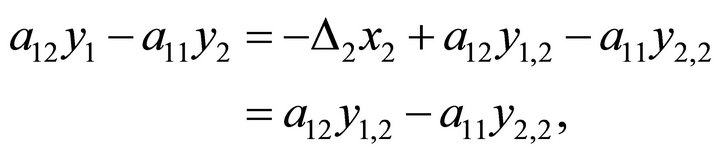
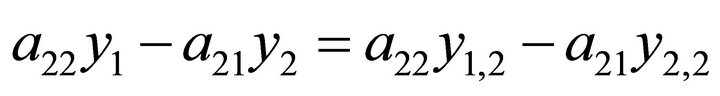 .
.
It directly follows from these relations that 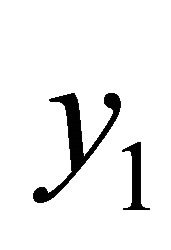
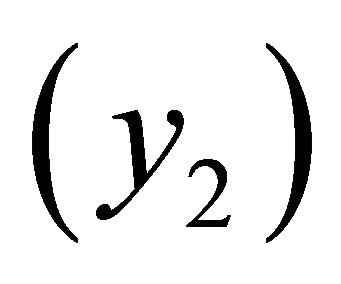 belongs to the closure of linear span of the remaining elements
belongs to the closure of linear span of the remaining elements 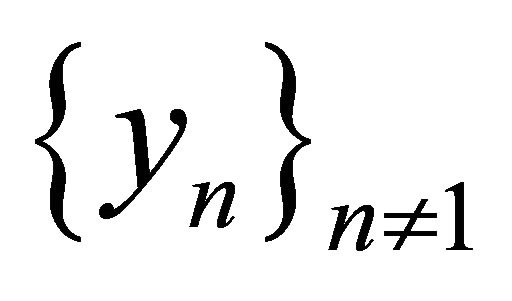
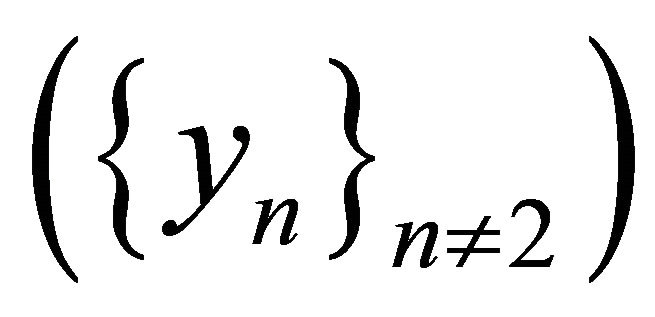 , i.e.
, i.e. 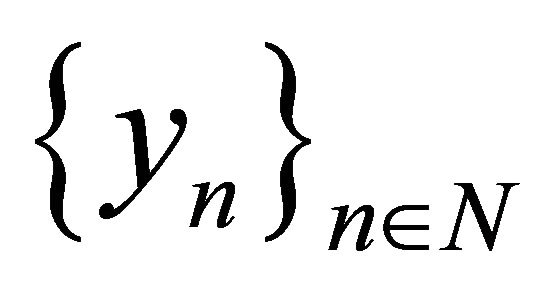 is not minimal in X. Consequently, for
is not minimal in X. Consequently, for 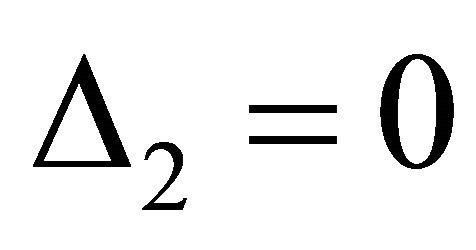 the system
the system  doesn’t form a basis. This reasoning is taken to an arbitrary
doesn’t form a basis. This reasoning is taken to an arbitrary 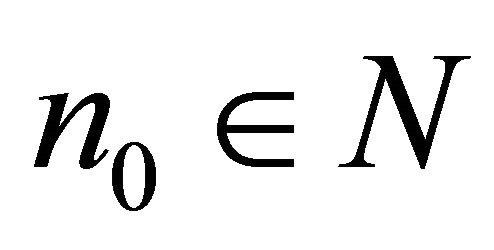 very easily. ڤ
very easily. ڤ
Before proceeding the main results, we accept the following basic assumptions concerning the functions of 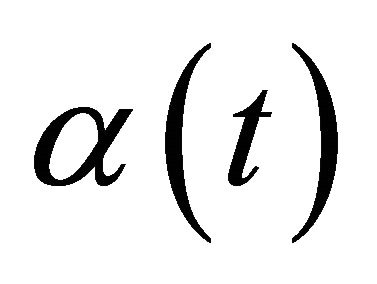 and
and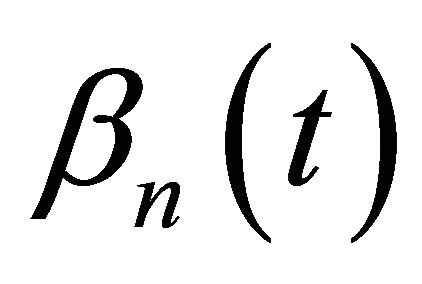 .
.
1) 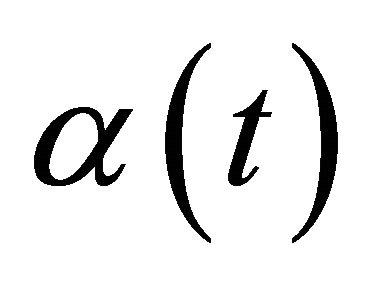 is a piecewise-Holder function on
is a piecewise-Holder function on ,
, 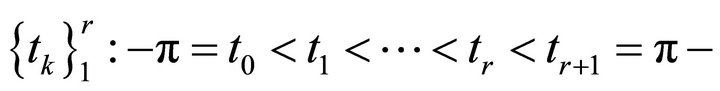 are its discontinuity points of first kind;
are its discontinuity points of first kind;
Denote the jumps of the function 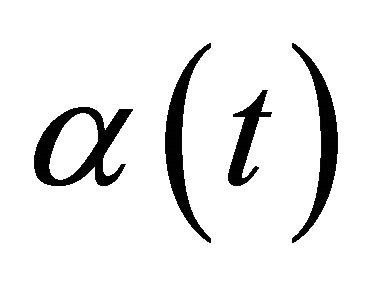 at the points
at the points  by
by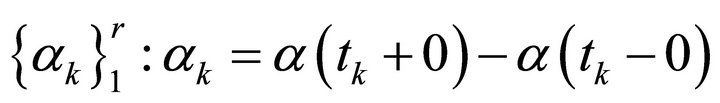 .
.
Let the condition 2)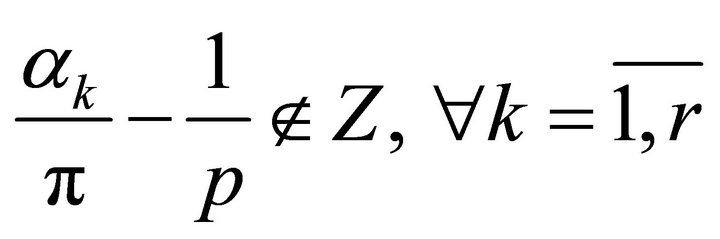 , be fulfilled.
, be fulfilled.
3) The functions 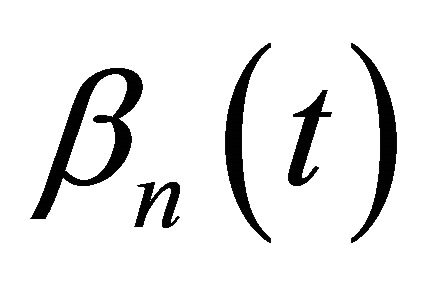 have the following asymptotic relations
have the following asymptotic relations
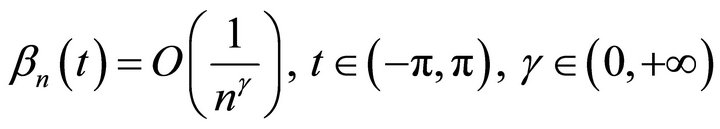 . (7)
. (7)
3. Basic Results
At first we consider the system of exponents
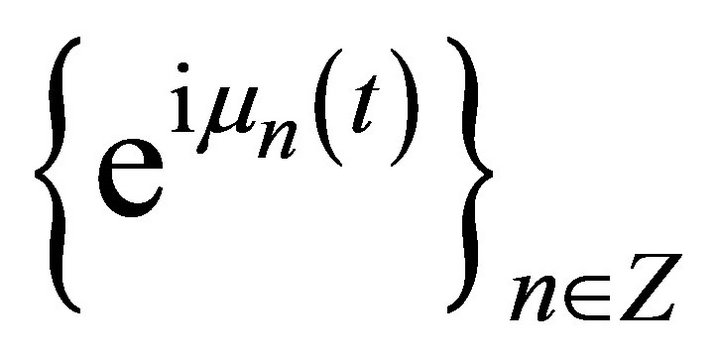 , (8)
, (8)
where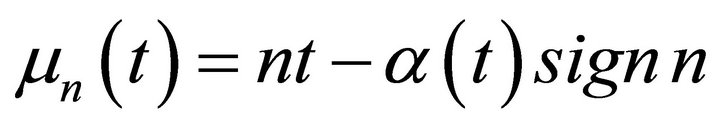 ,
,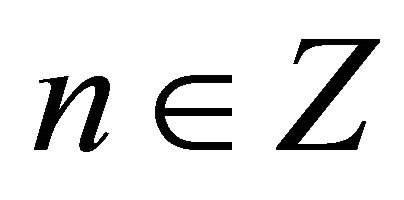 . For the basicity of system (8) in
. For the basicity of system (8) in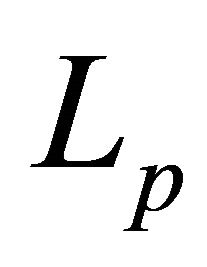 , the results of the paper [23] will be used. Represent system (8) in the form
, the results of the paper [23] will be used. Represent system (8) in the form
 , (9)
, (9)
(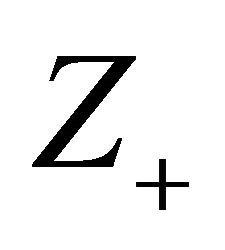 are non-negative integers). Let the condition 2) be fulfilled. Finding
are non-negative integers). Let the condition 2) be fulfilled. Finding  from the following inequalities
from the following inequalities :
:
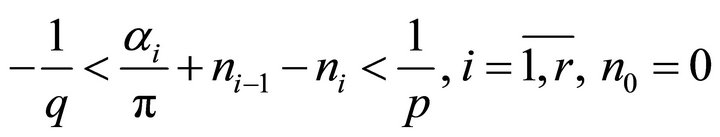 , (10)
, (10)
assume
 . (11)
. (11)
Based on Theorem 1 of the paper [23] we can directly conclude the following Statement 1. Let the conditions 1), 2) be fulfilled for the function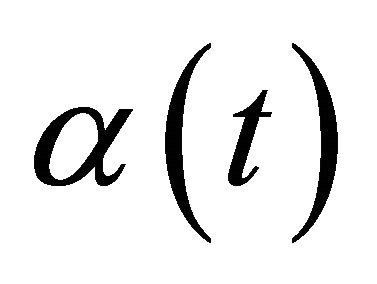 . Suppose that
. Suppose that . The system (9)
. The system (9)
forms a basis for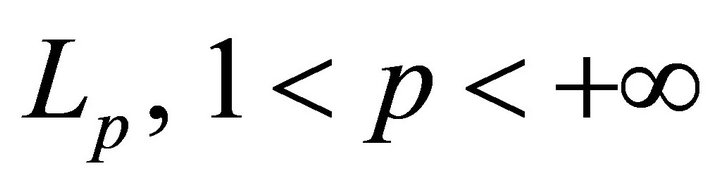 , (for p = 2 a Riesz basis) if and only if it holds the inequality
, (for p = 2 a Riesz basis) if and only if it holds the inequality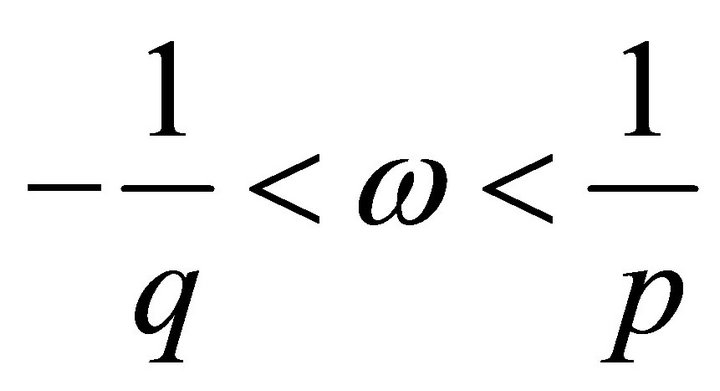 .
.
We will use the following statement obtaining from the results of the paper [24].
Statement 2. If system (9) forms a basis for ,
, 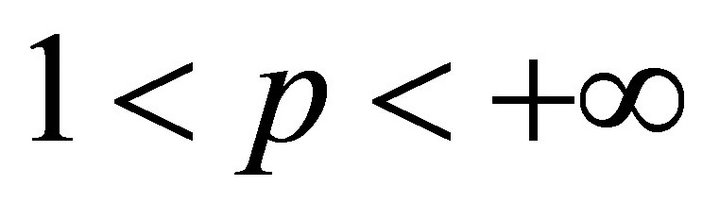 , then it is isomorphic to the classic system of exponents
, then it is isomorphic to the classic system of exponents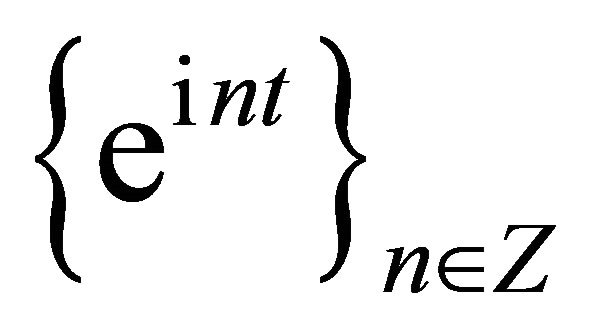 .
.
So, let system (8) form a basis for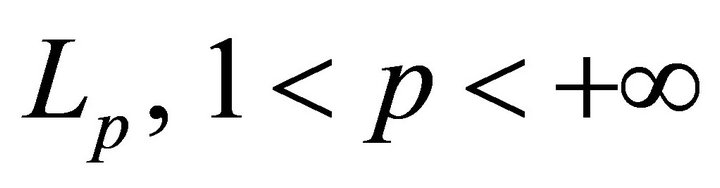 . Denote by
. Denote by 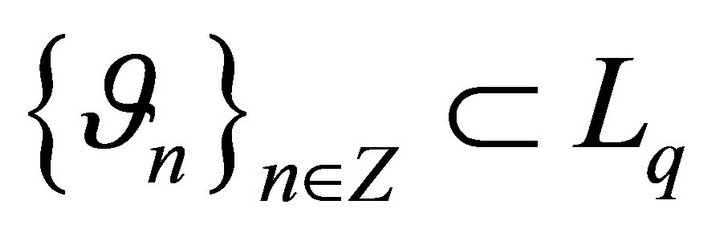 a system biorthogonal to it. Let
a system biorthogonal to it. Let 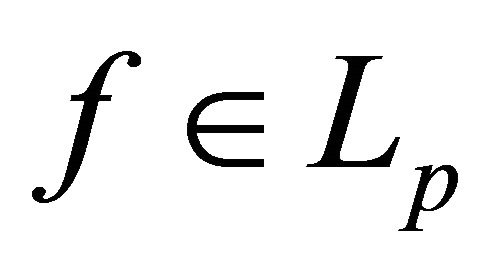 and
and 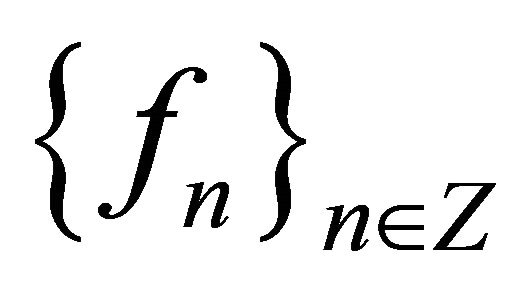 be its biorthogonal coefficients by system (8), i.e.
be its biorthogonal coefficients by system (8), i.e.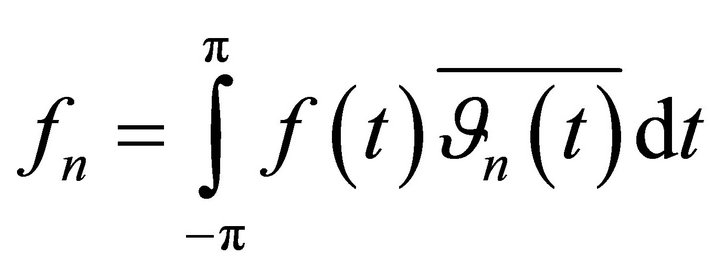 ,
,  , where
, where 
is complex conjugation. The following theorem can be directly concluded from Statement 2.
Theorem 1. Let system (8) forms a basis for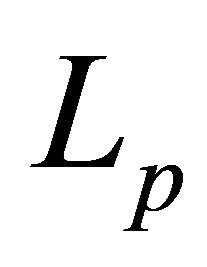 ,
,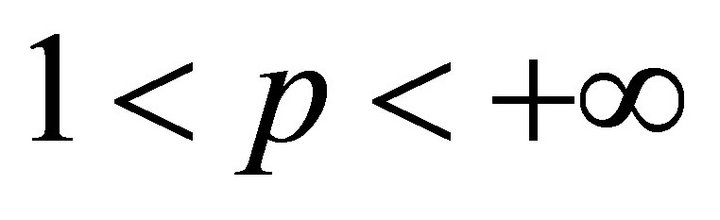 . Then there hold:
. Then there hold:
1) Let 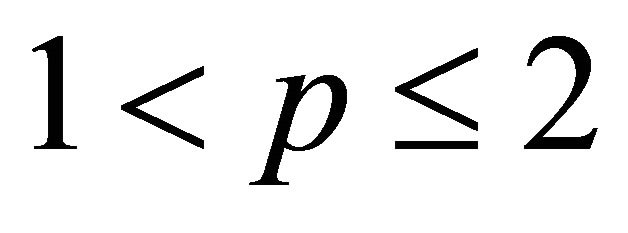 and
and . Then
. Then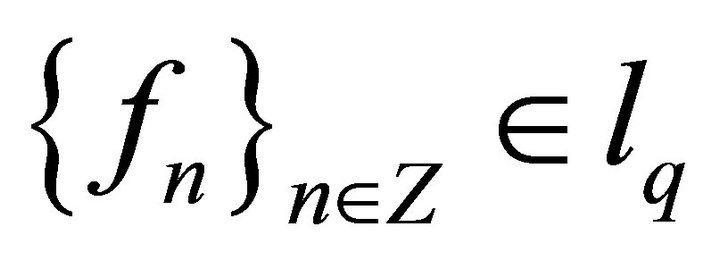 , and
, and
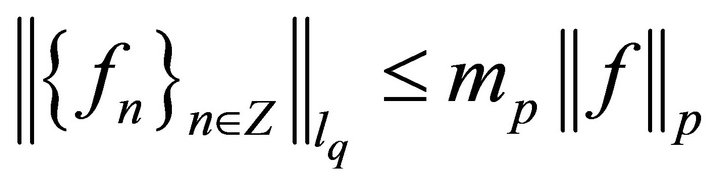 is fulfilled, where mp is a constant independent of f,
is fulfilled, where mp is a constant independent of f, 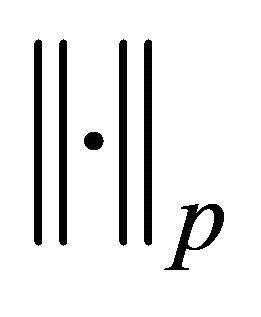 is an ordinary norm in Lp.
is an ordinary norm in Lp.
2) Let 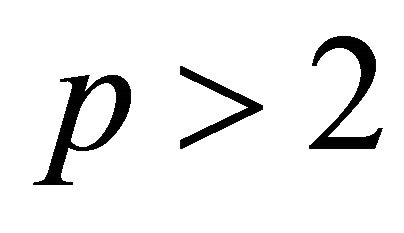 and the sequence of numbers
and the sequence of numbers 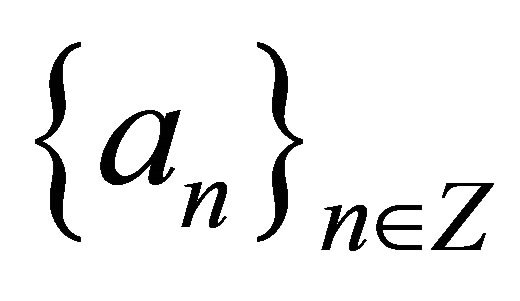 belong to
belong to . Then
. Then 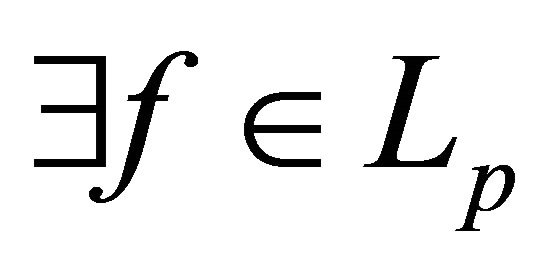 such that
such that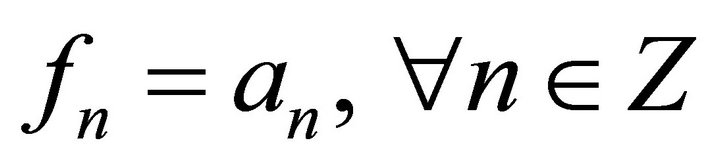 moreover
moreover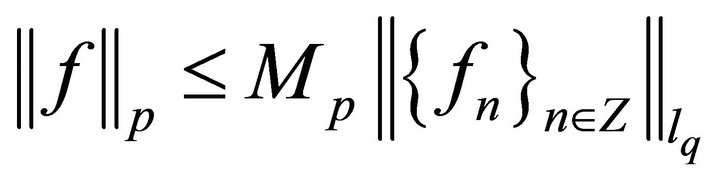 , where Mp is a constant independent of
, where Mp is a constant independent of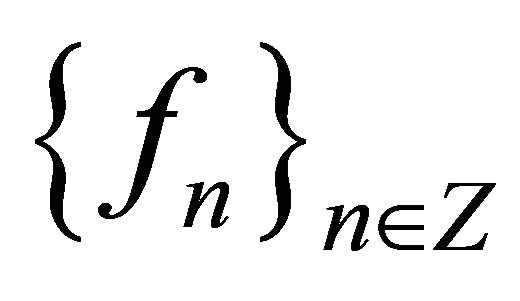 .
.
Now, study the basicity of system (3) in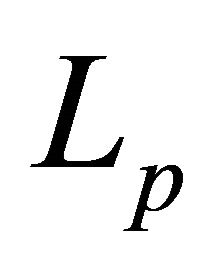 . We have
. We have
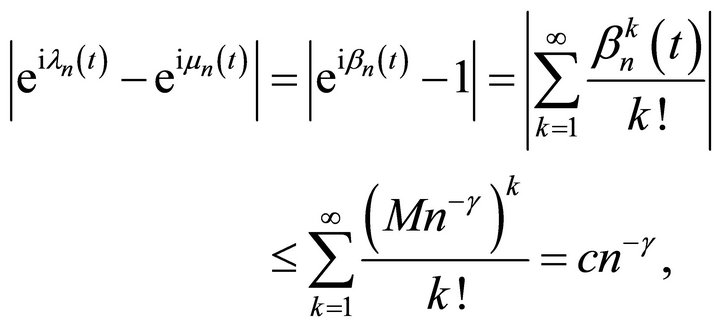
where c is a constant independent of n. The last inequality follows from (7).
Consider the different cases.
1) Let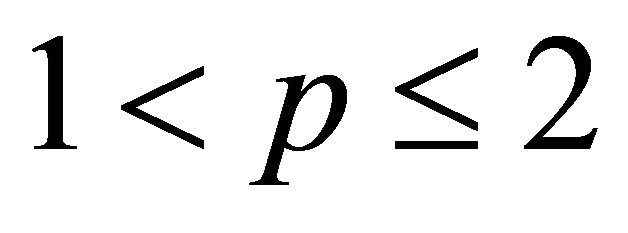 ,
, . We have
. We have
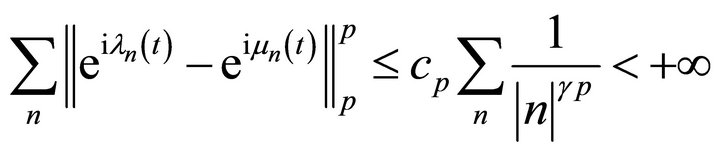 .
.
Assume that all the conditions of Statement 1 are fulfilled. Then, system (8) forms a basis for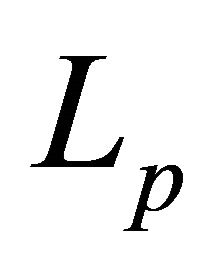 . Thus, by Statement 2 it forms a
. Thus, by Statement 2 it forms a 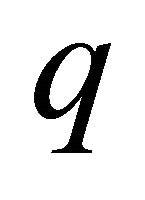 -basis for
-basis for 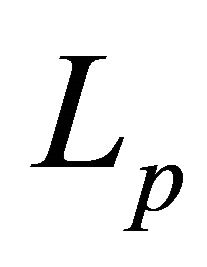 in this case. Let
in this case. Let 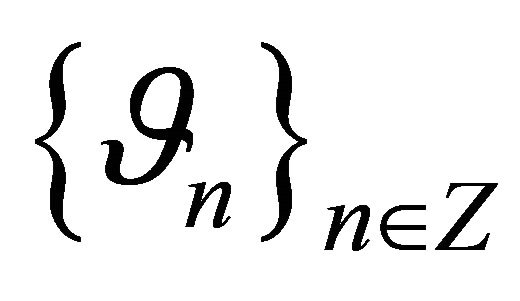 be a system biorthogonal to it. Consider the operator
be a system biorthogonal to it. Consider the operator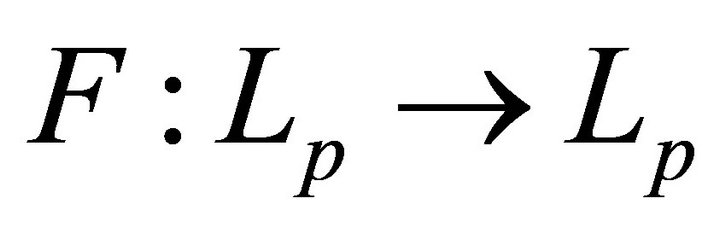 :
:
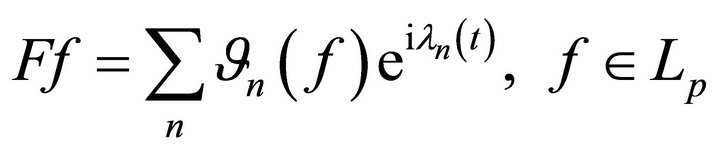 , (12)
, (12)
where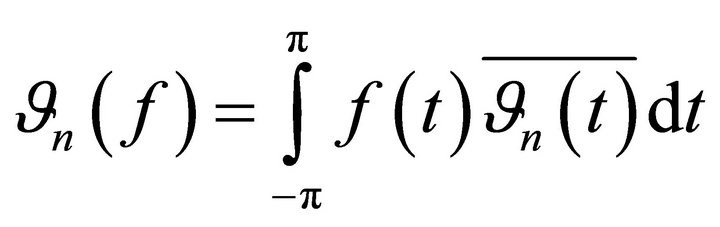 ,
,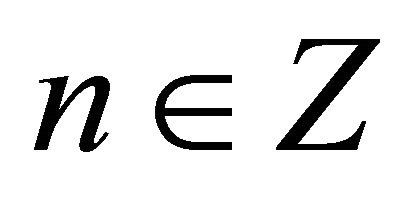 . By Lemma 2 operator (12) is Fredholm in Lp. It is easy to see that
. By Lemma 2 operator (12) is Fredholm in Lp. It is easy to see that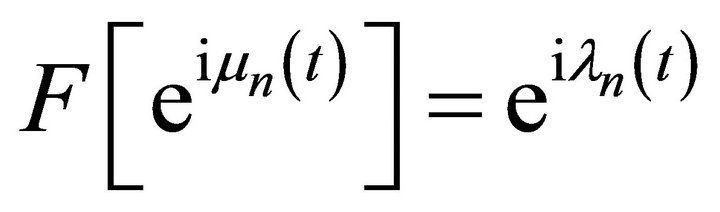 ,
,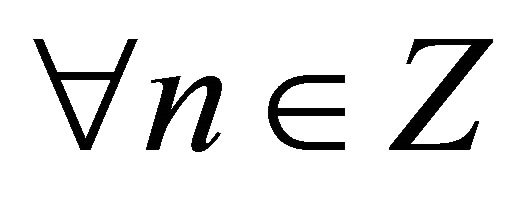 . Then, the statement of Lemma 1 is valid for system (3).
. Then, the statement of Lemma 1 is valid for system (3).
2) Let ,
,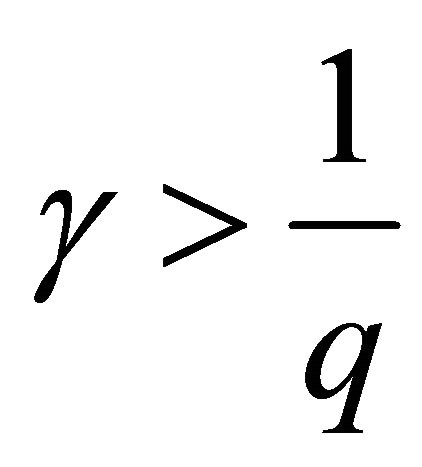 . It is clear that
. It is clear that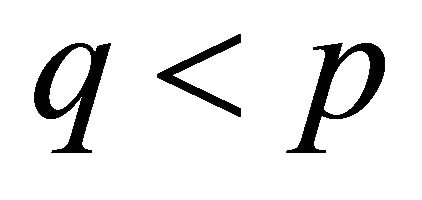 .
.
Consequently, for  it is valid
it is valid , where
, where 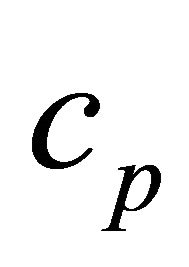 depends only on p. Assume that all the conditions of Statement 1 are fulfilled. Consequently, system (8) forms a basis for Lp. It is clear that
depends only on p. Assume that all the conditions of Statement 1 are fulfilled. Consequently, system (8) forms a basis for Lp. It is clear that 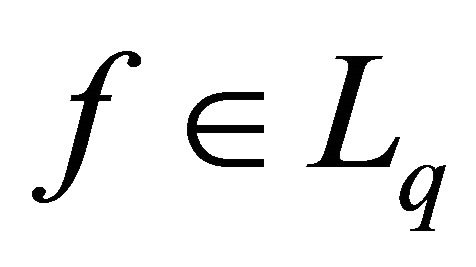 and
and . Then, from Theorem 1 we obtain that
. Then, from Theorem 1 we obtain that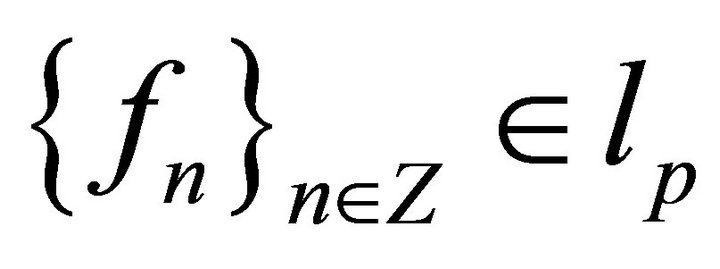 , where
, where 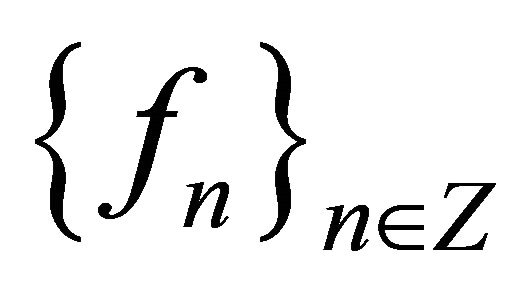 are the orthogonal coefficients of f by system (8). From the same theorem we obtain:
are the orthogonal coefficients of f by system (8). From the same theorem we obtain:
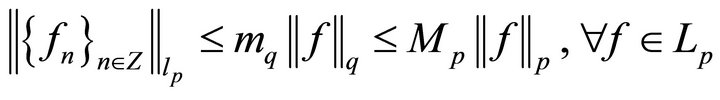 where the constant Mp is independent of f. Thus, system (8) forms a p-basis in Lp. It is easy to see that systems (3) and (8) q-close in Lp. Consider operator (12). Further, we behave similarly to case I. Hence the validity of the following theorem is proved.
where the constant Mp is independent of f. Thus, system (8) forms a p-basis in Lp. It is easy to see that systems (3) and (8) q-close in Lp. Consider operator (12). Further, we behave similarly to case I. Hence the validity of the following theorem is proved.
Theorem 2. Let asymptotic Formula (4) hold, the function 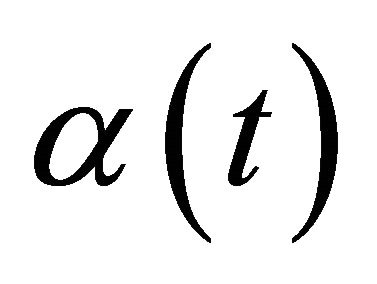 satisfy the conditions 1), 2) and for the function
satisfy the conditions 1), 2) and for the function 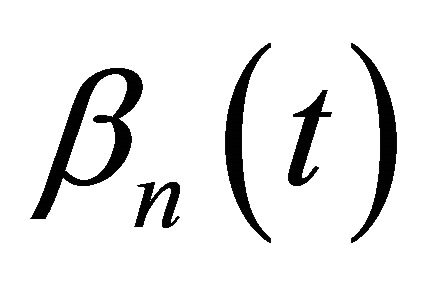 the relations (7) be valid. Assume that it holds
the relations (7) be valid. Assume that it holds
 where
where ,
,  is defined from expressions (10)(11). Then, the following properties for system (3) in Lp are equivalent:
is defined from expressions (10)(11). Then, the following properties for system (3) in Lp are equivalent:
1) Complete;
2) Minimal;
3)  -linearly independent;
-linearly independent;
4) Forms a basis isomorphic to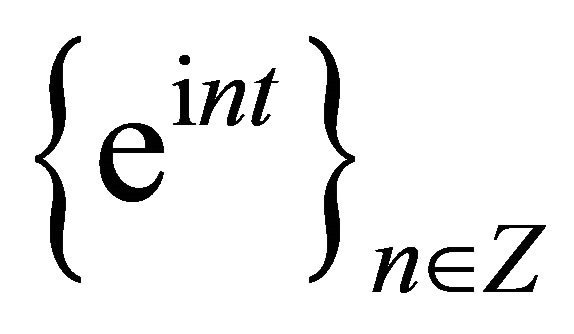 .
.
In sequel, we will consider a case, when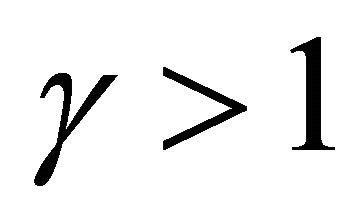 . In this case, it is obvious that it holds
. In this case, it is obvious that it holds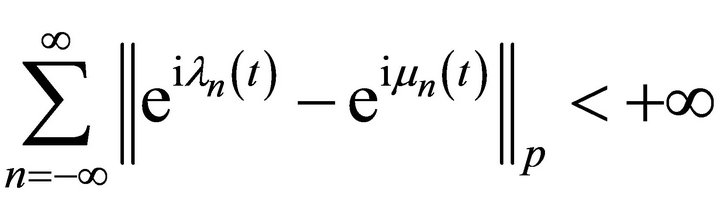 .
.
Let all the conditions of Theorem 2 be fulfilled. Then the system  forms a basis for Lp. Denote by
forms a basis for Lp. Denote by
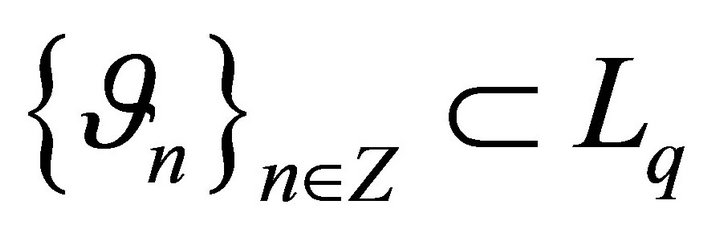 a system biorthogonal to it. Assume
a system biorthogonal to it. Assume . It is clear that
. It is clear that

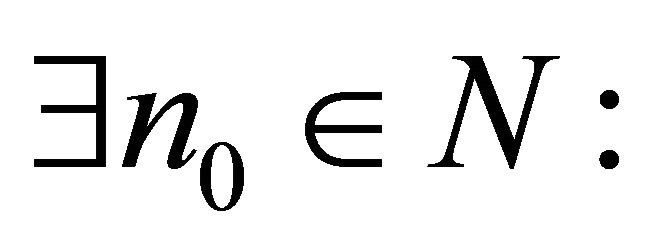
Consider the functions
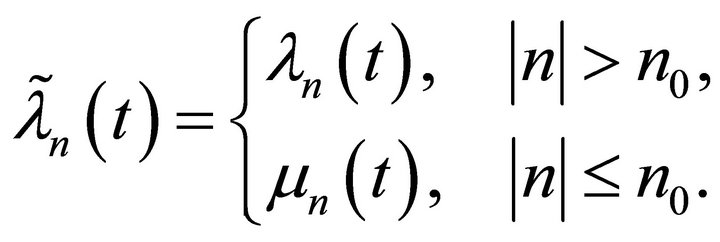
Thus, it holds
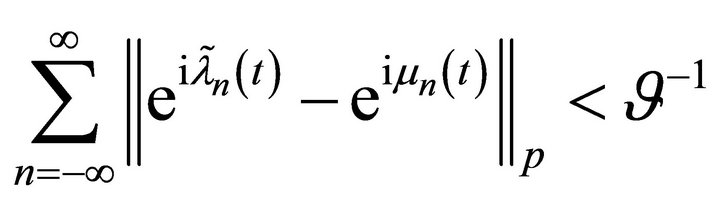 .
.
Then, as it follows from Theorem KMR, the system  forms a basis isomorphic to
forms a basis isomorphic to 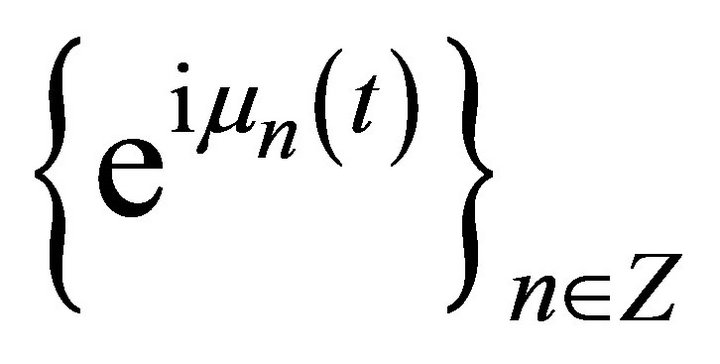 for Lp. System (3) and the basis
for Lp. System (3) and the basis 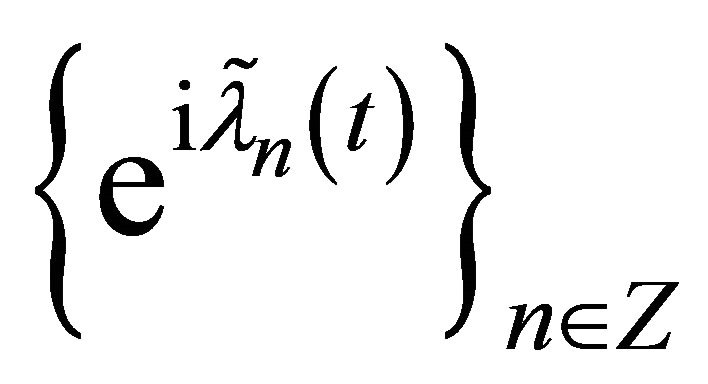 differ by a finitely many elements. By
differ by a finitely many elements. By  denote a biorthogonal system to this basis. Consider
denote a biorthogonal system to this basis. Consider
 , (13)
, (13)
It is obvious that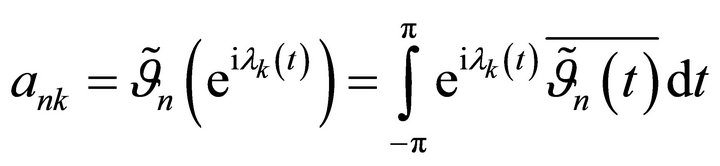 , n,
, n,
 . Denote by
. Denote by 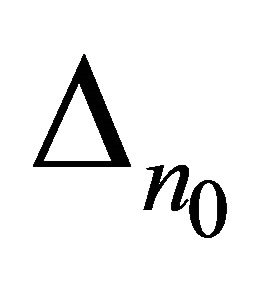 the following determinant
the following determinant
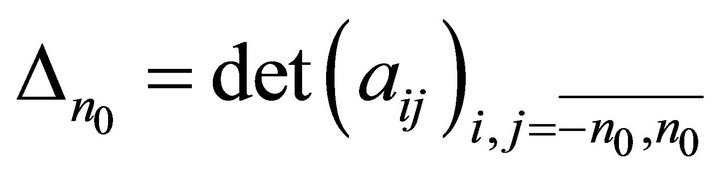 . (14)
. (14)
It is clear that if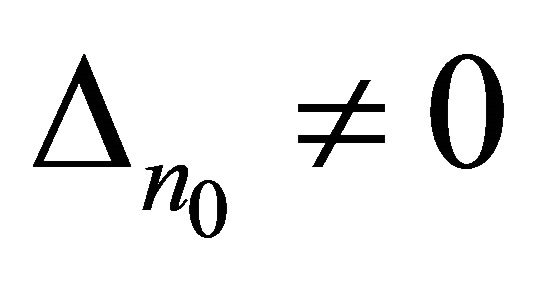 , in the expansion (13) the elements
, in the expansion (13) the elements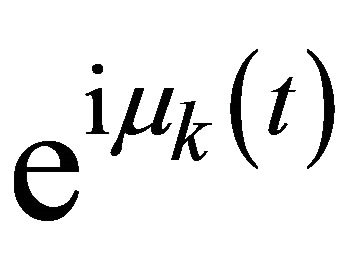 ,
, 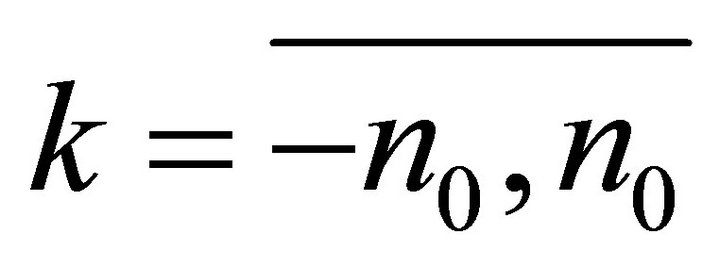 may be replaced by the elements
may be replaced by the elements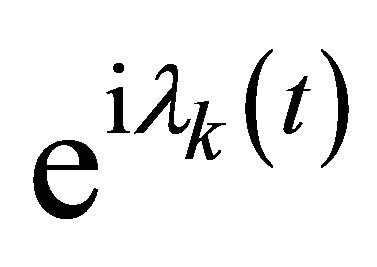 ,
, . Then the system
. Then the system 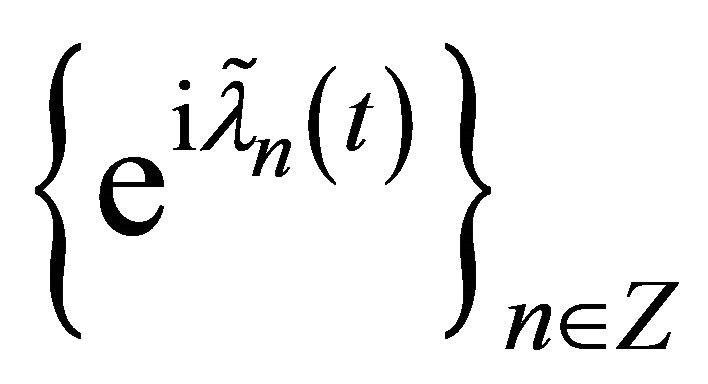 forms a basis for
forms a basis for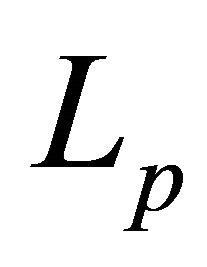 , since
, since 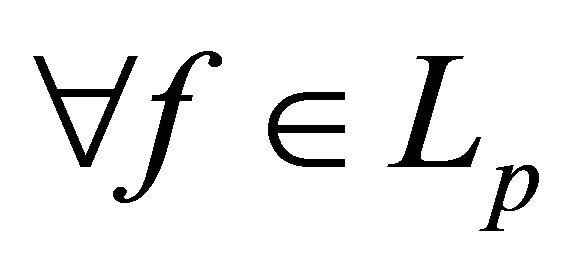 has the expansion
has the expansion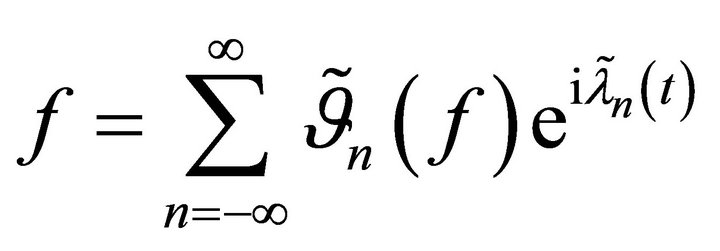 . Hence, it directly follows that if
. Hence, it directly follows that if
 , then
, then 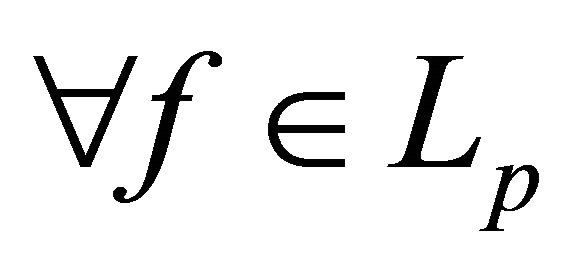 has an expansion by system (3), i.e. it is complete in
has an expansion by system (3), i.e. it is complete in . Consider the operator
. Consider the operator
 . We have
. We have

where 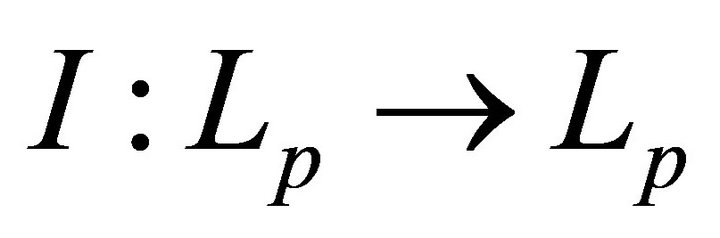 is an identity operator, and T is an operator generated by the second summand. Fredholm property F in
is an identity operator, and T is an operator generated by the second summand. Fredholm property F in  follows from finite-dimensionality of the operator
follows from finite-dimensionality of the operator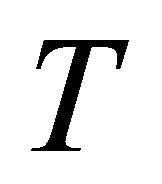 . It is clear that
. It is clear that
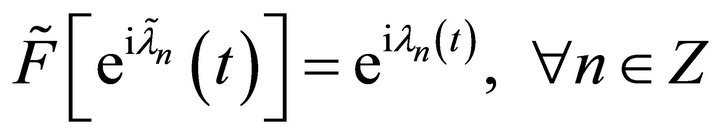 .
.
Then from Lemma 1 we obtain the basicity of system (3) in Lp. Conversely, if system (3) forms a basis for Lp, then as it follows from Lemma 3,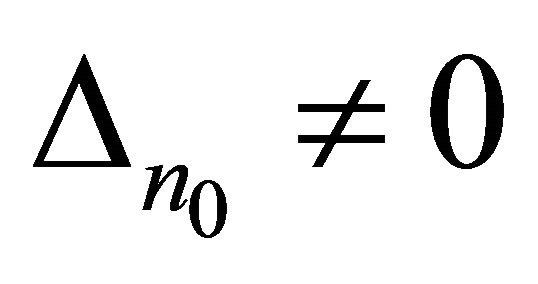 . Thus, we established that under accepted conditions system (3) forms a basis for Lp if the determinant determined by expression (14) is not zero.
. Thus, we established that under accepted conditions system (3) forms a basis for Lp if the determinant determined by expression (14) is not zero.
Thus, we proved the following.
Theorem 3. Let all the conditions of Theorem 2, where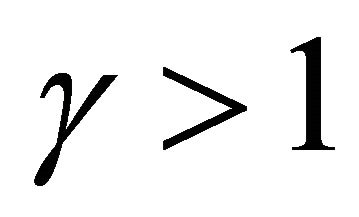 , be fulfilled. The determinant
, be fulfilled. The determinant 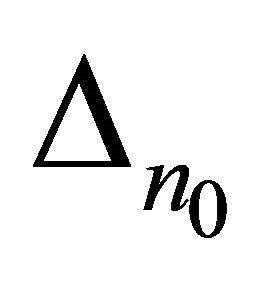 is determined by expression (14). System (3) forms a basis for Lp,
is determined by expression (14). System (3) forms a basis for Lp, 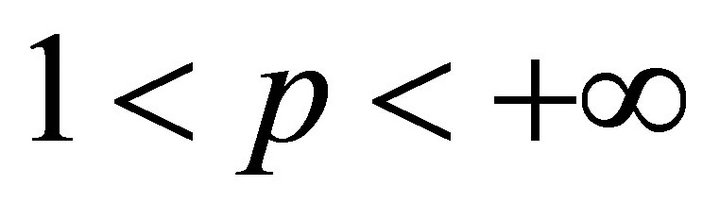 , if and only if
, if and only if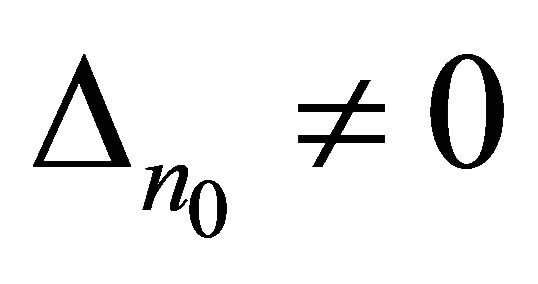 .
.
Now, consider the case when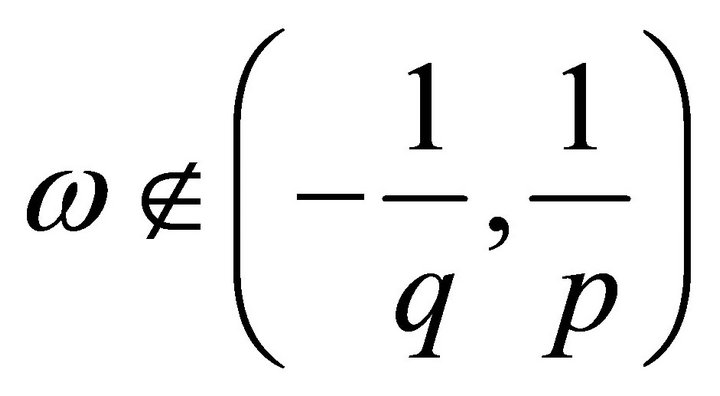 . Let for example,
. Let for example,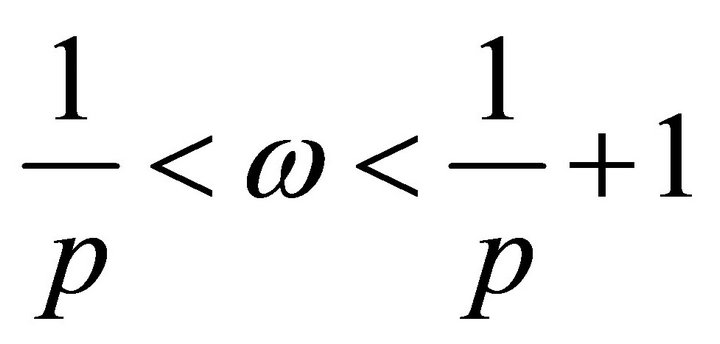 . In this case, as it follows from Theorem 1 of the paper [23], the system
. In this case, as it follows from Theorem 1 of the paper [23], the system
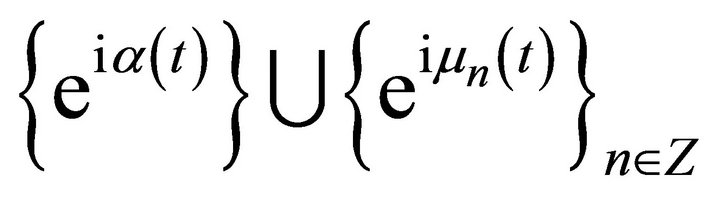 , (15)
, (15)
forms a basis for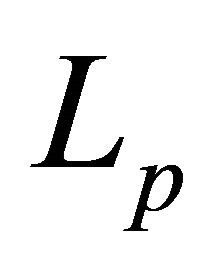 . Consider the system
. Consider the system
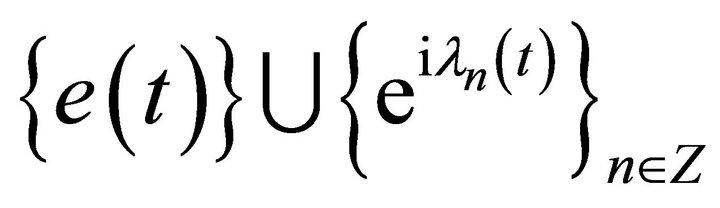 , (16)
, (16)
where 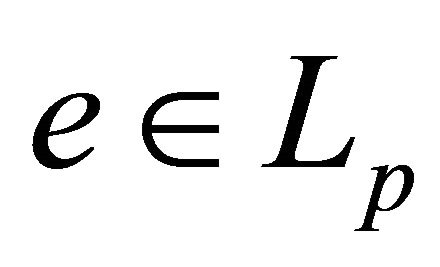 is a function. Let the conditions 1), 2) be fulfilled for system (3) and
is a function. Let the conditions 1), 2) be fulfilled for system (3) and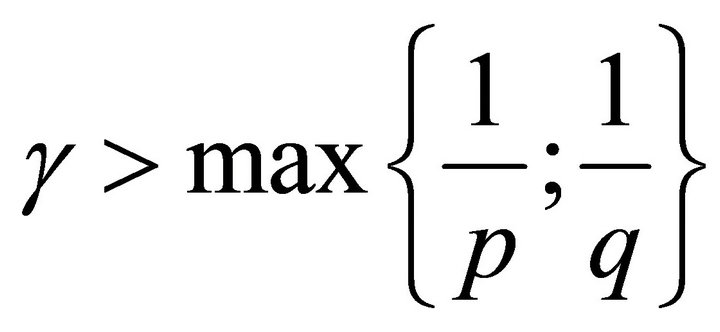 . Then, it is easy to see that system (16) and basis (15) are
. Then, it is easy to see that system (16) and basis (15) are 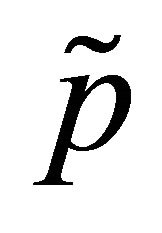 -close in
-close in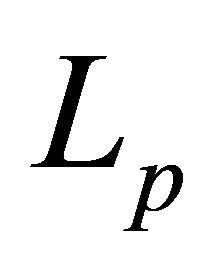 , where
, where 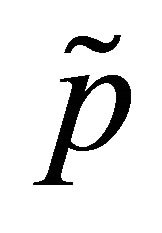 is determined by the formula
is determined by the formula
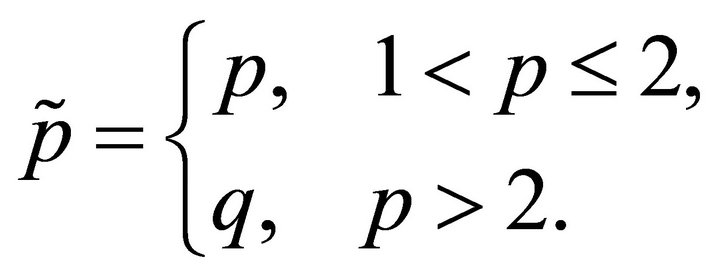
Consequently, system (3) is not complete in Lp. The remaining cases, when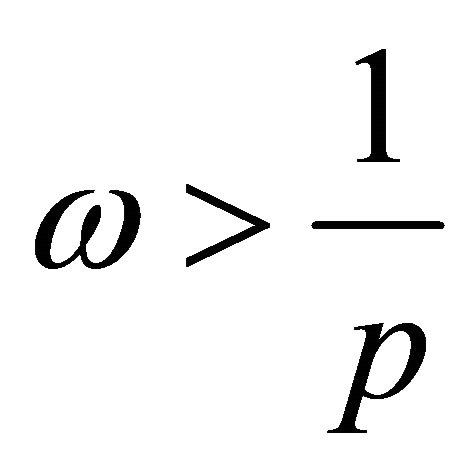 , are proved in the similar way.
, are proved in the similar way.
Consider a case, when , for example,
, for example,
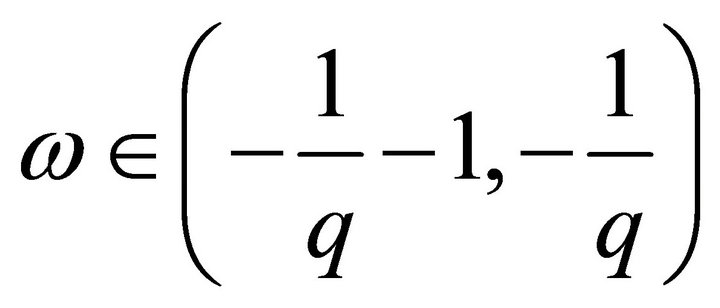 . In this case, again as it follows from Theorem 1 of the paper [23], the system
. In this case, again as it follows from Theorem 1 of the paper [23], the system
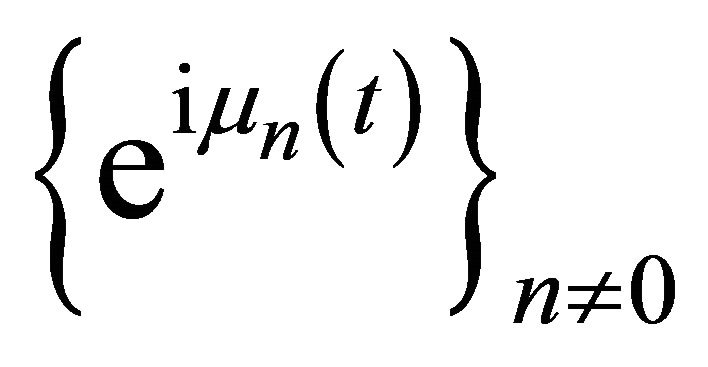 , (17)
, (17)
forms a basis for Lp. If the conditions 1), 2) are fulfilledthen basis (17) and the system  are
are 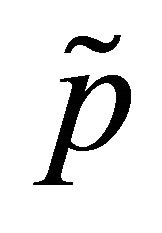 -close in Lp. Consequently, system (3) is not minimal in Lp. The remaining cases, when
-close in Lp. Consequently, system (3) is not minimal in Lp. The remaining cases, when , are proved similarly.
, are proved similarly.
Therefore, we obtain the following final result for the basicity of system (3) in Lp.
Theorem 4. Let asymptotic formula (4) hold, where the functions 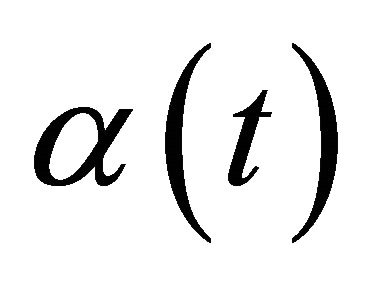 and
and  satisfy the conditions 1), 2), 3). The variable
satisfy the conditions 1), 2), 3). The variable  be determined from relations
be determined from relations
(10), (11) and let . Then for
. Then for 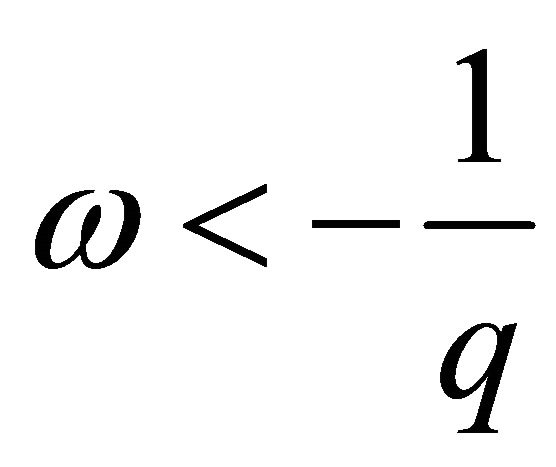 system (3) is not minimal in
system (3) is not minimal in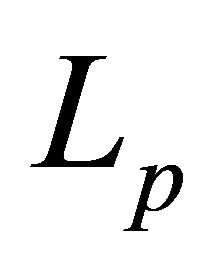 ; for
; for  it is not complete in
it is not complete in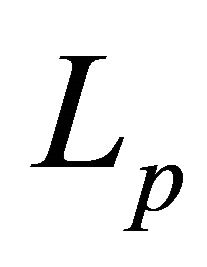 . For
. For 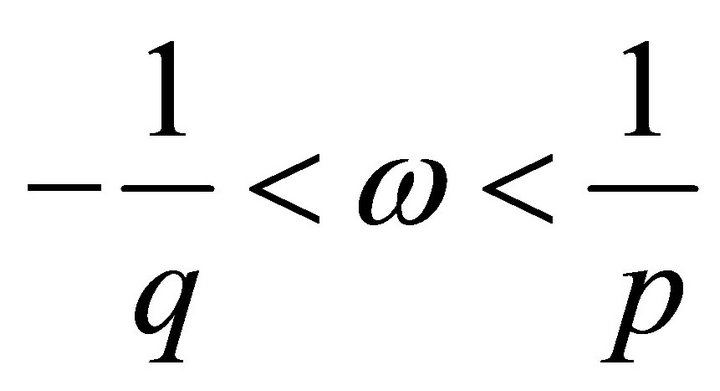 the following properties of system (3) in
the following properties of system (3) in  are equivalent:
are equivalent:
1) Complete;
2) Minimal;
3)  -linearly independent;
-linearly independent;
4) Forms a basis isomorphic to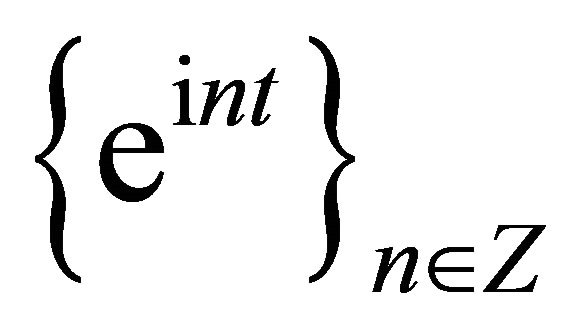 ;
;
5)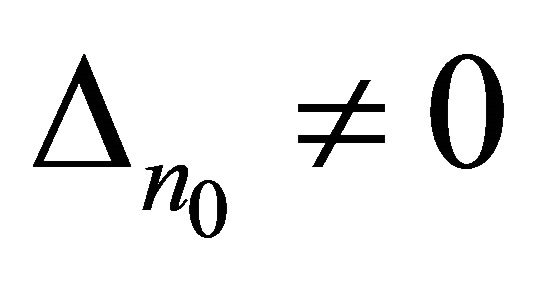 , where
, where 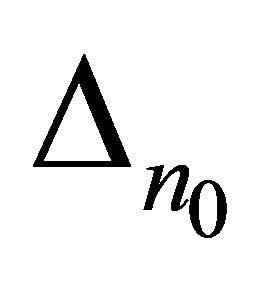 is determined by expression (14).
is determined by expression (14).
Indeed, equivalence of properties 1)-4) follows directly from Lemma 1. Equivalence of conditions 4) and 5) is proved.
4. Conclusions
Taking into account the obtained results, we can summarize this work as follows.
Perturbed system of exponents, the phase of which may has different asymptotic behavior in different parts of the basic interval , is studied in this work. It should be noted that it’s probably the first time the problem of basicity is considered for such a system. Under certain conditions on the functions defining the phase, we prove that this system may have a finite defect in Lp,
, is studied in this work. It should be noted that it’s probably the first time the problem of basicity is considered for such a system. Under certain conditions on the functions defining the phase, we prove that this system may have a finite defect in Lp, . Moreover, it either forms a basis for Lp, or it is not complete and not minimal in Lp.
. Moreover, it either forms a basis for Lp, or it is not complete and not minimal in Lp.
5. Acknowledgements
The authors express their deepest gratitude to Professor B. T. Bilalov, for his attention and valuable guidance to this article.
REFERENCES
- R. Paley and N. Wiener, “Fourier Transforms in the Complex Domain,” American Mathematical Society, Providence, 1934.
- N. Levinson, “Gap and Density Theorems,” American Mathematical Society, Providence, 1940.
- R. M. Young, “An Introduction to Non-Harmonic Fourier Series,” Springer, Berlin, 1980, p. 246.
- A. M. Sedletskii, “Classes of Analytic Fourier Transformations and Exponential Approximations,” Fizmatlit, Moscow, 2005.
- Ch. Heil, “A Basis Theory Primer,” Springer, Berlin, 2011, p. 534. doi:10.1007/978-0-8176-4687-5
- O. Christensen, “An Introduction to Frames and Riesz bases,” Springer, Berlin, 2003, p. 440.
- D. L. Russell, “On Exponential Bases for the Sobolev Spaces Over an Interval,” Journal of Mathematical Analysis and Applications, Vol. 87, No. 2, 1982, pp. 528-550. doi:10.1016/0022-247X(82)90142-1
- X. He and H. Volkmer, “Riesz Bases of Solutions of Sturm-Lioville Equations,” Journal of Fourier Analysis and Applications, Vol. 7, No. 3, 2001, pp. 297-307. doi:10.1007/BF02511815
- H. Miklos, “Inverse Spectral Problems and Closed Exponential Systems,” Annals of Mathematics, Vol. 162, No. 2, 2005, pp. 885-918. doi:10.4007/annals.2005.162.885
- A. M. Sedletskii, “Nonharmonic Analysis,” Functional Analysis, Itogi Nauki i Tekhniki Seremennaya Matematika i ee Prilozheniya Tematicheskie Obzory, Vol. 96, 2006, pp. 106-211.
- L. H. Larsen, “Internal Waves Incident upon a Knife Edge Barrier,” Deep Sea Research, Vol. 16, No. 5, 1969, pp. 411-419.
- S. A. Gabov and P. A. Krutitskii, “On Larsen’s Nonstationary Problem,” Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, Vol. 27, No. 8, 1987, pp. 1184- 1194.
- P. A. Krutitskii, “Small Non-Stationary Vibrations of Vertical Plates in a Channel with a Stratified Fluid,” USSR Computational Mathematics and Mathematical Physics, Vol. 28, No. 6, 1988, pp. 166-176.
- E. I. Moiseev and N. Abbasi, “Basis Property of Eigenfunctions of the Generalized Gasedynamic Problem of Frankl with a Nonlocal Oddness Condition and with the Discontinuity of the Gradient of Solution,” Differential Equations, Vol. 45, No. 10, 2009, pp. 1452-1456.
- V. A. Ilin, “Mixed Problem Describing the Damping Process of a Bar Consisting of Two Sections of Different Density and Elasticity Provided that the Time of Wave’s Passage in Each of These Sections Coincide,” Trudi Instituta Matematiki i Mekhaniki Uro RAN, Vol. 269, 2010, pp. 132-141.
- I. S. Lomov, “Non-Smooth Eigenfunctions in Problems of Mathematical Physics,” Differential Equations, Vol. 47, No. 3, 2011, pp. 358-365.
- L. M. Lujina, “Regularity of Spectral Problems with Additional Conditions at the Inner Points,” Matematicheskie Zametki, Vol. 49, No. 3, 1991, pp. 151-153.
- B. T. Bilalov and S. M. Farahani, “On Perturbed Bases of Exponential Functions with Complex Coefficients,” Transactions of NAS of Azerbaijan, Vol. 56, No. 4, 2011, pp. 45-50.
- I. Singer, “Bases in Banach Spaces, I,” Springer, Berlin, 1970, p. 673. doi:10.1007/978-3-642-51633-7
- I. T. Hochberg and A. S. Markus, “On Stability of Bases of Banach and Hilbert Spaces,” Izvestiya Akademii Nauk Moldavskoj SSR, No. 5, 1962, pp. 17-35.
- B. T. Bilalov and T. R. Muradov, “On Equivalent Bases in Banach Spaces,” Ukrainian Mathematical Journal, Vol. 59, No. 4, 2007, pp. 551-554. doi:10.1007/s11253-007-0040-1
- B. T. Bilalov, “Bases from Exponents, Cosines and Sines Being Eigen Functions of Differential Operators,” Differential Equations, Vol. 39, No. 5, 2003, pp. 1-5.
- B. T. Bilalov, “Basicity of Some Systems of Exponents, Cosines and Sines,” Differential Equations, Vol. 20, No. 1, 1990, pp. 10-16.
- B. T. Bilalov, “On Isomorphism of Two Bases,” Fundamentalnaya i Prikladnaya Matematika, Vol. 1, No. 4, 1995, pp. 1091-1094.

