Applied Mathematics
Vol.4 No.2(2013), Article ID:28214,3 pages DOI:10.4236/am.2013.42055
A Generalization of the Input-Output Pollution Control Model and Product Selection
Department of Mathematics, University of Tennessee, Chattanooga, USA
Email: aniekan-ebiefung@utc.edu
Received December 5, 2012; revised January 5, 2013; accepted January 12, 2013
Keywords: Input-Output; Pollution; Environment; Technology; Leontief Production Model
ABSTRACT
The input-output pollution control model given in [1] is generalized. The generalization makes it easier for the model to handle many problem instances. A linear program is used to solve the new model. An example is given to show that the new model can handle classes of problems that the original model cannot handle.
1. Introduction
The Leontief input-output model has been used to address many environmental problems. Leontief [2,3] and Leontief and Daniel [4] extended the production model to address pollution related problems. Ebiefung [5] used input-output techniques to select environmentally friendly industrial technologies. The recent model by Ebiefung and Isaac [1] used input-output techniques to select an optimal combination of products that an economy should produce in order to satisfy demands and meet pollution emission requirements simultaneously. Other usage of the input-output techniques to address environmental concerns can be found in the monographs by Miller and Blair [6] and Raa [7].
The model by Ebiefung and Isaac [1] has equalities. This limits the usefulness of the model in the following ways. It makes it difficult to find a solution if the associated matrix is ill-conditioned. Moreover, if the model has many solutions, including negative solutions, the standard method for solving linear systems may pick up a negative solution, which will violate the non negativity assumptions of the model. The generalized model presented in this paper will avoid these problems and so enhances the ability of the pollution control model to handle more problem instances. An algorithm is provided for solving the generalized model.
The structure of the rest of the paper is as follows. In Section 2, the I-O pollution control model is presented. A generalization of the model, as well as an algorithm for solving it, is provided in Section 3. Concluding remarks are given in Section 4.
2. The Input-Output Pollution Control Model
We start with the following notation.
Constants:
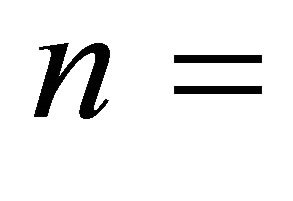 number of sectors in the economy
number of sectors in the economy
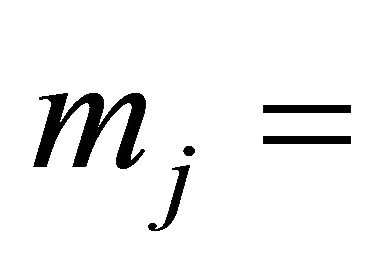 number of different types of products that sector j can produce,
number of different types of products that sector j can produce, 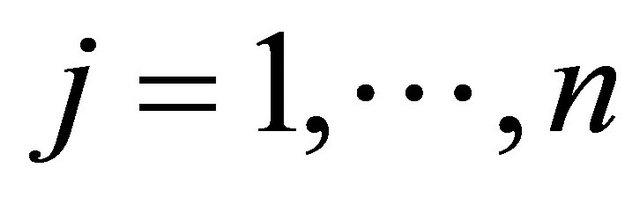
 amount of pollutants to be produced by sector j,
amount of pollutants to be produced by sector j, 
 amount of pollutants that sector j should produce in order to satisfy external demands,
amount of pollutants that sector j should produce in order to satisfy external demands, 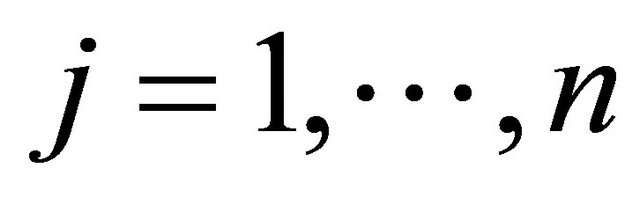
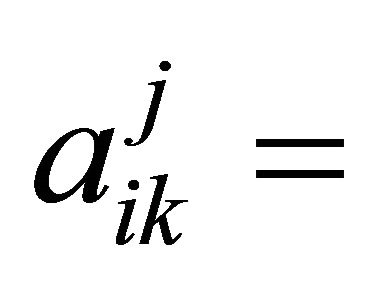 output of pollutants by product i in sector j needed by sector k to produce one unit of its pollutants,
output of pollutants by product i in sector j needed by sector k to produce one unit of its pollutants, 
Matrices:
For each j,  let
let
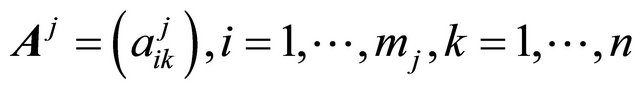
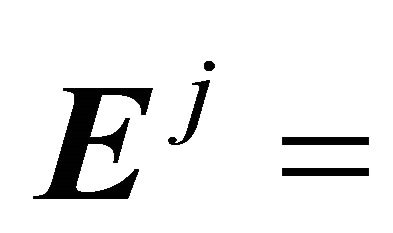 an
an  × n matrix with 1s in column j and zeros in all other columns
× n matrix with 1s in column j and zeros in all other columns
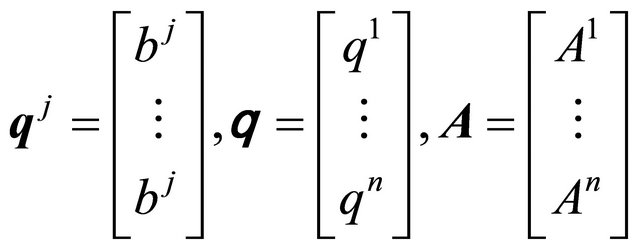 (1)
(1)
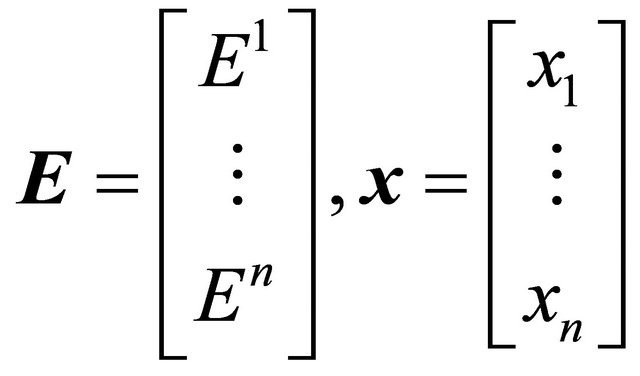 (2)
(2)
If we set , then
, then

and . The matrix Aj represents the pollution matrix for sector j, and A the pollution matrix for the whole economy.
. The matrix Aj represents the pollution matrix for sector j, and A the pollution matrix for the whole economy.
The I-O Pollution Control Model (IOPCM): Given the input-output pollution coefficient matrix  and the amount of pollutants
and the amount of pollutants  required by all sectors of the economy to meet external demands, find x, the amount of pollutants to be produced by all sectors of the economy so that IOPCM:
required by all sectors of the economy to meet external demands, find x, the amount of pollutants to be produced by all sectors of the economy so that IOPCM:![]() (3)
(3)
where .
.
The product chosen for production by sector j is one whose row satisfies Equation (3). If many rows from sector j satisfy Equation (3), then sector j can produce any of those products, the choice of which may depend on other considerations.
3. A Generalization of the IOPCM
The model given in Equation (3), as well as the Leontief model (1986), is not flexible due to strict equalities. To make sure the model can handle many realistic problems, we generalize it in this section and give an algorithm for solving the generalized version.
The Generalized Model (GIOPCM): Given the inputoutput pollution matrix A and the amount of pollutants q that all sectors require for external demands, find x, the amount of pollutants to be produced by all the sectors, so that GIOPCM:![]() (4)
(4)
where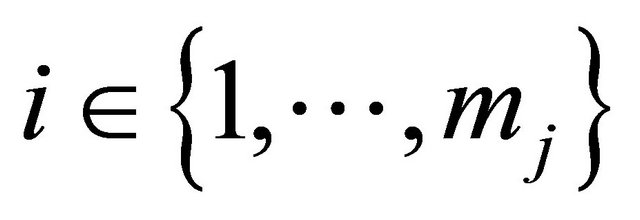 .
.
We assume that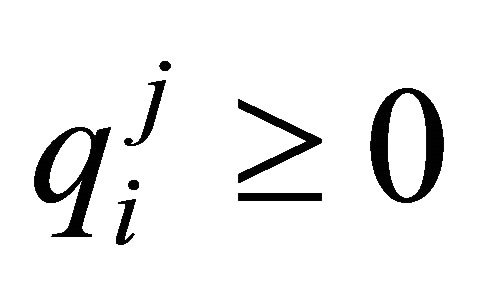 , if product i is to be produced during the period and will generate
, if product i is to be produced during the period and will generate 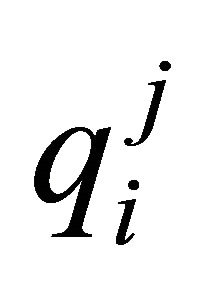 amount of pollutants; and
amount of pollutants; and , if product i is available in inventory but −
, if product i is available in inventory but − amount of pollutants were generated during production.
amount of pollutants were generated during production.
The linear programming problem below can be used to solve the generalized model. We need the following definitions.
Definition 1. An m × n matrix N, m ≥ n, is called a vertical block matrix of type 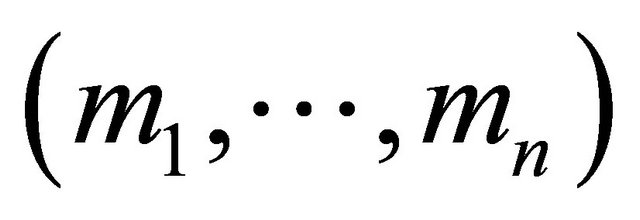 if it is partitioned row-wise into n blocks such that the jth block,
if it is partitioned row-wise into n blocks such that the jth block,  , is of dimension
, is of dimension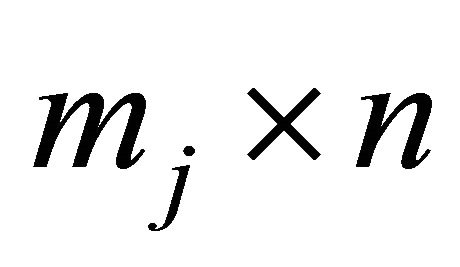 . The matrix E – A, associated with the pollution model, is a vertical block matrix. The jth block,
. The matrix E – A, associated with the pollution model, is a vertical block matrix. The jth block,  , is associated with the pollution matrix for sector j.
, is associated with the pollution matrix for sector j.
Definition 2. A matrix M is a representative sub-matrix of E – A if row j of M comes from block j of E – A. Since each block in E – A has dimension , the number of representtative sub-matrices is
, the number of representtative sub-matrices is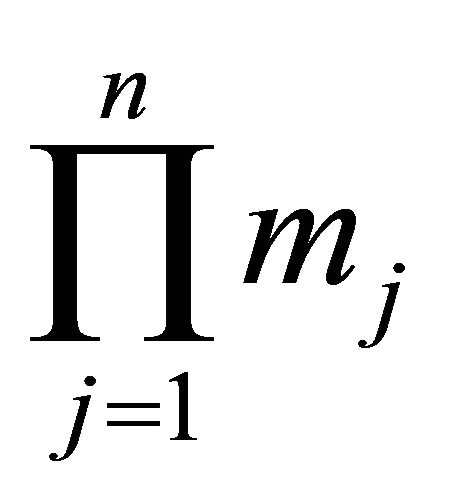 .
.
3.1. Algorithm
Step 1: Let  be the representative sub matrices of E – A, where
be the representative sub matrices of E – A, where .
.
Step 2: For each λ, solve the LP:
 (5)
(5)
where  and the rows in
and the rows in 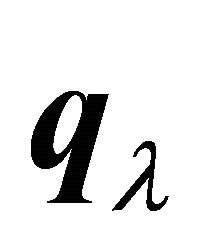 correspond to the rows in
correspond to the rows in .
.
Step 3: If the system in Step 2 has a solution for some index, 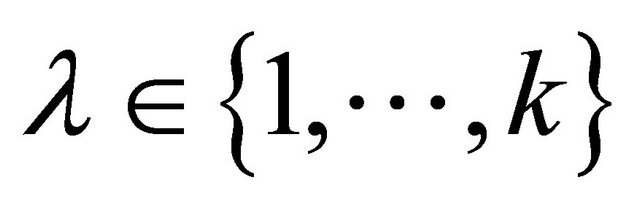 , with objective value less than or equal to the total allowable pollutant level for the economy, then the GIOPCM has a solution. The products chosen correspond to the rows in
, with objective value less than or equal to the total allowable pollutant level for the economy, then the GIOPCM has a solution. The products chosen correspond to the rows in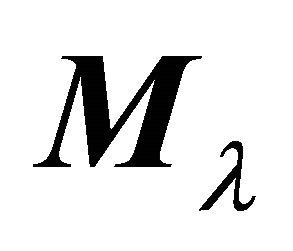 .
.
Otherwise, the system has no solution. Stop.
Proof: The proof of the Algorithm is straightforward and so is omitted.
3.2. Example 1
We use the generalized model to resolve Example 2 in [1]. Consider an economy consisting of two sectors: agriculture and manufacturing. Let the pollution technology matrix be as given in Table 1.
Suppose that these products have made all production criteria set by the sectors. We want to find the product that each sector should select for production in order to meet both internal and external demands as well as satisfy pollution emission requirement.
Using the notation of the Algorithm, we have

Solving the LPs in Step 2 of the Algorithm, we obtain the solutions in Table 2.
Table 1. Input-output pollution coefficients and demand quantities.

Table 2. Solutions to example 2.

From Table 2, we see that the solution in row 1 satisfies the allowed pollutant level. Thus the agricultural and manufacturing sectors should select wheat and cloth, respectively, for production. This correct solution in row 1 is the same as the solution in column 2 of Example 2 in [1], obtained by solving a linear system. However, solving the problem using a linear program has the advantage that sensitivity analysis can be performed when there are changes to the problem parameters.
The next example shows that the generalized model is capable of solving problem instances that the equality model cannot handle.
3.3. Example 2
Consider an economy that has two sectors in which the input-output pollution matrix A and the amount of pollutants q that all sectors require for external demands are given by:

The negative entry in q, the (2,1) entry, implies that goods that can emit 200 units of pollutants for external demands are in inventory and will not be actually produced. Solving the model by the linear system provided in [1, Step 2 of the Algorithm] using MATLAB 6.5, we obtained the solution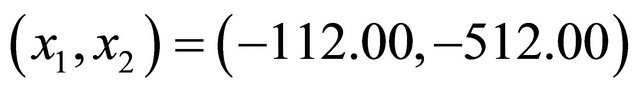 which does not satisfy the non-negativity conditions. However, solving the corresponding linear program in the generalized model using LINDO 6.1, we obtained the solution
which does not satisfy the non-negativity conditions. However, solving the corresponding linear program in the generalized model using LINDO 6.1, we obtained the solution . Appropriately,
. Appropriately,  , which shows that no pollutants are to be produced by Sector 2 since equivalent amount of goods are available in inventory, as was assumed in the model. Thus the generalized model is able to handle this problem instance, while the equality model cannot.
, which shows that no pollutants are to be produced by Sector 2 since equivalent amount of goods are available in inventory, as was assumed in the model. Thus the generalized model is able to handle this problem instance, while the equality model cannot.
4. Conclusion
A generalization of the input-output pollution control model formulated in [1] is provided. By means of an example, we show that the new model can handle problem instances that the old equality model cannot. An algorithm is presented for solving the generalized model. Apart from its flexibility in dealing with more variety of problems, solving the new model with a linear program allows for sensitivity analysis when problem parameters are changed.
REFERENCES
- A. A. Ebiefung and I. Isaac, “An Input-Output Pollution Control Model and Product Selection,” Journal of Mathematics Research, Vol. 4, No. 55, 2012, pp. 1-7.
- W. W. Leontief, “Environmental Repercussions and the Economic Structure: An Input-Output Approach,” The Review of Economics and Statistics, Vol. 52, No. 3, 1970, pp. 241-260. doi:10.2307/1926294
- W. W. Leontief, “Input-Output Economics,” 2nd Edition, Oxford University Press, New York, 1986.
- W. W. Leontief and F. Daniel, “Air Pollution and the Economic Structure: Empirical Results of Input-Output Computations,” In: A. Brody and A. P. Carter, Eds., Input-Output Techniques, North-Holland, Amsterdam, 1972, pp. 9-23.
- A. A. Ebiefung, “Choice of Technology, Industrial Pollution, and the Vertical Linear Complementarity Problem,” Global Journal of Mathematical Sciences, Vol. 9, No. 2, 2010, pp. 113-120.
- R. M. Miller and P. D. Blair, “Input-Output Analysis: Foundations and Extensions,” Prentice Hall, Upper Saddle River, 1985.
- T. T. Raa, “Linear Analysis of Competitive Economies,” LSE Handbook in Economics, Harvester Wheatsheaf, New York, 1995.

