ABSTRACT

In this paper we examine the large deviations principle (LDP) for sequences of classic Cramér-Lundberg risk processes under suitable time and scale modifications, and also for a wide class of claim distributions including (the non-superexponential) exponential claims. We prove two large deviations principles: first, we obtain the LDP for risk processes on 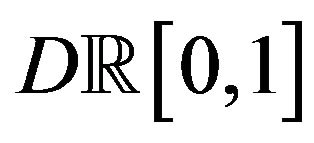with the Skorohod topology. In this case, we provide an explicit form for the rate function, in which the safety loading condition appears naturally. The second theorem allows us to obtain the LDP for Aggregate Claims processes on 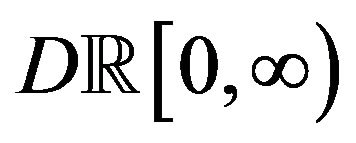with a different time-scale modification. As an application of the first result we estimate the ruin probability, and for the second result we work explicit calculations for the case of exponential claims.

1. Introduction

There is a wide literature on Large Deviation Techniques and Applications. Relevant to this paper are results by Mogulskii (1993), [1] who proved a Large Deviations result for independent, identically distributed (i.i.d.) random variables with generating functions finite on a neighborhood of the origin. In [2], Lynch and Sethuraman gave large deviations results for stochastic processes with independent and stationary increments. The analysis was done on the space of functions of bounded variation on endowed with the weak^*-topology. More general results were proved later, as Mogulskii and De Acosta did in [1,3,4] proving large deviations results for Lévy processes in very general settings.

For compound Poisson processes, Li and Pechersky [5], following results by Dobrushin and Pechersky [6], proved the LDP for multi-dimensional compound Poisson processes defined on 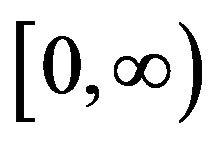with respect to the vague topology, and then strengthened it to the weakuniform topology introduced in [6].

The LDP for (reserve dependent premium with delayed claims) risk process was studied by Ganesh, Massi and Torrisi (2007) [7,8]. They proved the LDP with respect to the uniform topology in the case of superexponential claims i.e., claims for which the moment generating function is finite for every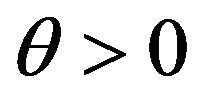. Later, in [7], they illustrated the connection between risk processes and queues. They applied their large deviations result (valid only in the case of super-exponential claims) to obtain an approximation for the probability of ruin and to propose an importance sampling parameter for simulation. The super-exponential claims are an interesting but very particular case, since distributions such as gamma (including exponential), Negative Binomial (including geometric) claims, are not of this type.

One way to deal with large deviations for risk processes is by proving the LDP for a sufficiently similar zero-mean Lévy process, and then using the Contraction Principle. That is the general approach we follow for Theorem 1: we examine the LDP for a sequence of risk processes with respect to the Skorohod topology under suitable time and scale modifications. We follow Mogulskii’s approach [1], whose results are based on Lynch and Sethuraman [2] to obtain an LDP for risk processes on 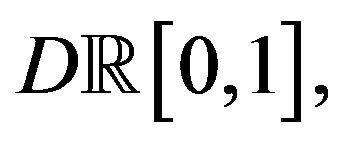and give quite explicit forms for the rate function.

Another way to prove Large Deviations results is by first analyzing the compound Poisson component, via working with random walks 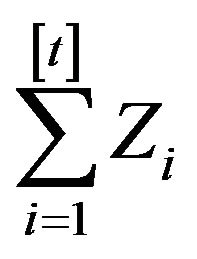or their linearized counterpart, proving the LDP, and then dealing with the random time via exponential equivalence of the times. In this direction there is work by Feng and Kurtz, [9] and our Theorem 2 for aggregate claims processes. The difficulty with this approach is that a Poisson process could hardly be exponentially equivalent to a continuous one, and it becomes necessary to use a cumbersome change in time-space scale. We prove Large Deviation results for a wide class of claim distributions including the non-super-exponential case of exponential claims.

We get the LDP for aggregate claims processes on 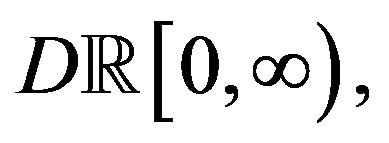with a suitable time-scale modification. Both results are LDP’s with respect to the Skorohod topology induced by the Skorohod distance, but the first one is in and the second is in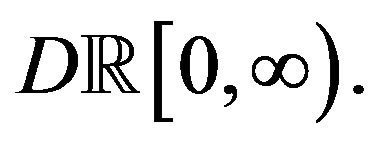

Although the vague topology is coarser than Skorohod’s, Li and Pechersky’s large deviations results do not imply ours (Theorem 1 below) because the space 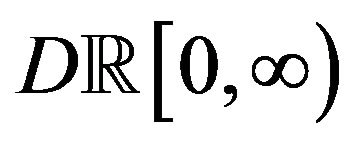is not reflexive, and non-trivial exponential tightness should be proved first. On the other hand, we do not work with super exponential claims: we only need the moment generating function to exist on an open neighborhood of the origin, and for this reason our result is more general.

Large Deviations techniques have been used to study ruin probabilities for risk process. A standard reference here is the book by Asmussen [10], references therein, and subsequent work by the author.

On a generalization of the model, Asmussen, Klüppelberg, and Mikosch, in [11,12], studied asymptotic results for the compound Poisson process when the size of the jumps has a heavy tail (the moment generating function of the claims is on the positive real numbers). In this case, the large deviations theory does not apply, the results are quite different, and that is not the subject of this paper.

The organization of the paper is as follows: First, we have one Section to state the basic notation, to describe previous results, and at the end we have a small discussion about the precise shape of the rate function: that is Section 2. In Section 3, we state the basic Hypotheses that are needed all along the work.

The main results, LDP Theorems 1 and 2, are stated in Sections 4 and 5, respectively. Both are proved in the same Section they are stated. Section 6 is devoted to the explicit calculations for the case of exponential claims. These calculations are combined in Corollary 1, and later used in Section 7 to estimate the probability of ruin for exponential claims, and also for more general claims.

2. Notation, Previous Results, and the Rate Function

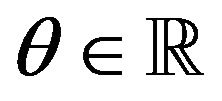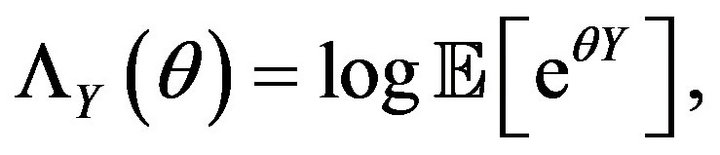For a random variable and, we denote by the moment generating function for Y, whenever it exists; its logarithmic generating function is and

shall denote the FenchelLegendre transform of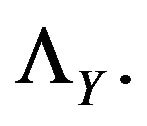

Let 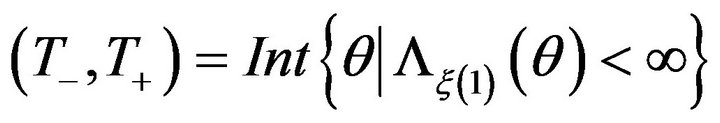denote the interior of the essential domain for the Laplace transform (and its log-generating function) of 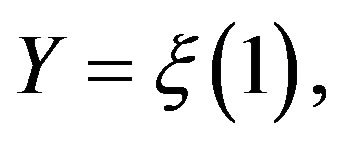where is a process to be specified.

Clearly,

The classical risk process is given by

(1)

and the following will be our assumptions regarding this process1) is a Poisson process, , that models the number of claims received at time.

2) 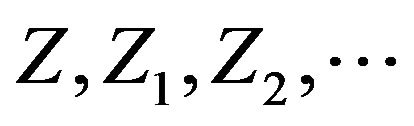are non negative i.i.d. random variables with mean 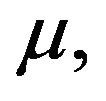independent of the process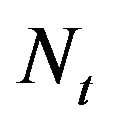. We shall always assume the moment generating function of, is finite for some (not necessarily for all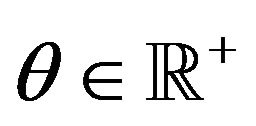). These variables represent the size of the claims. The compound Poisson term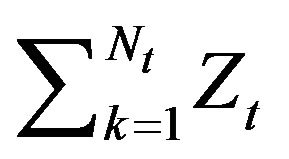

accounts for the aggregate claims.

3) 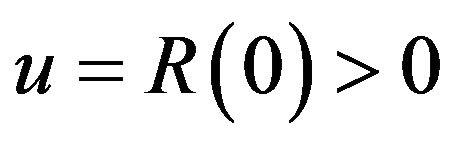is the initial capital or reserve.

4) is positive. The term represents the (non random and linear) premiums the company charges.

It is usually required to have a safety loading condition 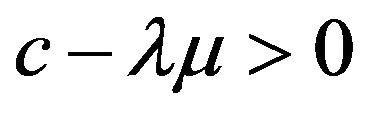to assure ruin does not occur almost surely. We do not need that condition for the moment; however, it shall appear when we give the explicit form of the large deviations rate function.

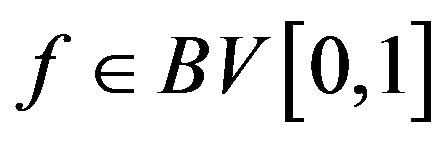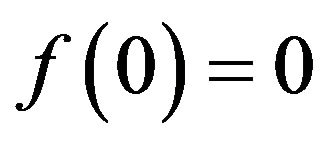For each bounded variation with and, let 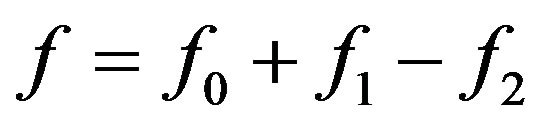be its standard decomposition such that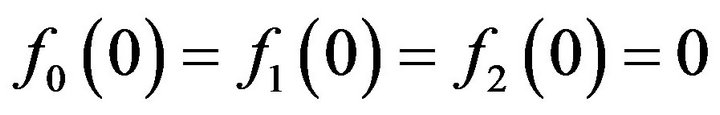, 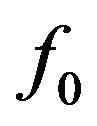is absolutely continuous with respect to the Lebesgue measure (here denoted as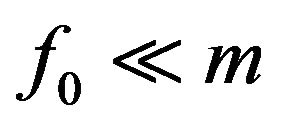), is the Hahn-Jordan decomposition for the singular part of f with respect to the Lebesgue measure. Recall that 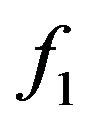and 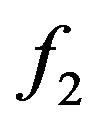are hence non-decreasing, and each one is singular with respect to (which shall be denoted).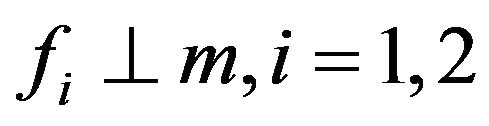

A standard representation for the characteristic function of a stationary process with independent increment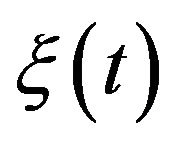s is

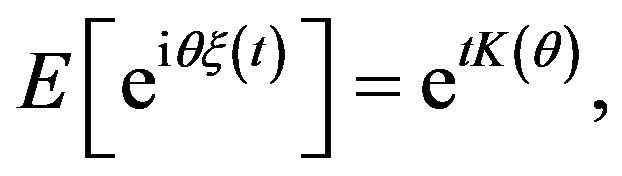
with

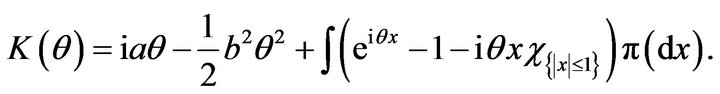
A regularity condition on the measure defined by the expression above, which will be needed in the main result (Theorem 1), is:

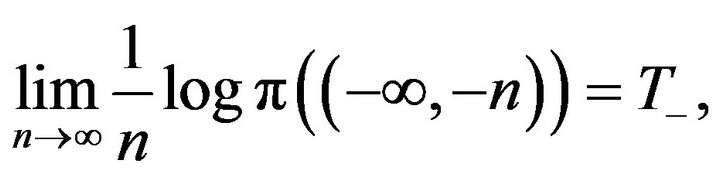(2)

and

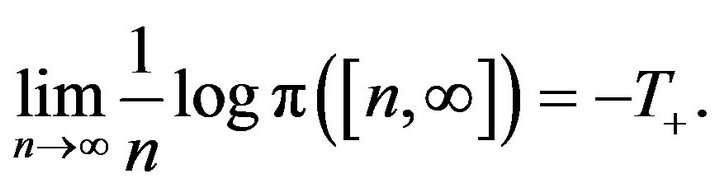
We shall apply Theorems 2.5 and 2.7 by Mogulskii [1] (see also [2]). We shall write here together all the results we apply, specialized to our settings, and use the notation defined above:

Proposition 1. (Mogulskii) Let 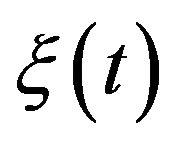be a stochastic process defined on 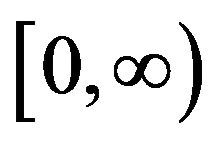with values in Assume it has stationary independent increments, and also suppose

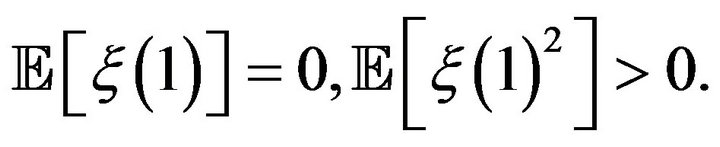
If 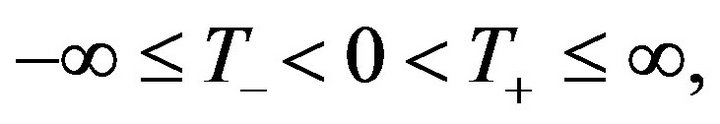then ULDP: 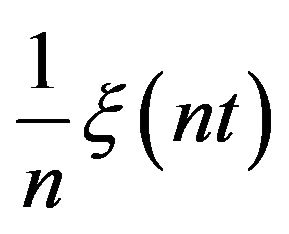satisfies the upper large deviations principle with respect to the completed Skorohod topology, with good rate function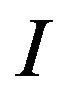. LLDP: If, additionally, the regularity condition

(2) is satisfied, then the same sequence 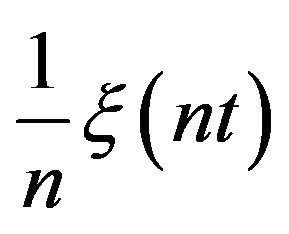satisfies the lower large deviations principle with respect to the completed Skorohod topology, with the same rate function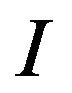. The rate function 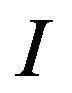is

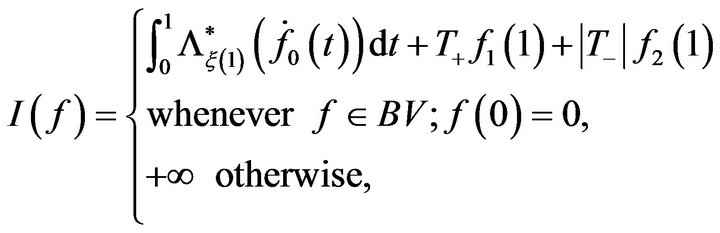(3)

where

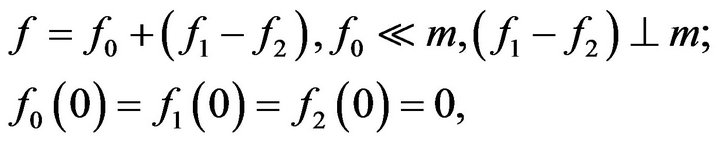
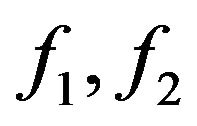are non-decreasing, and with the understanding that If then the ULDP holds also with the uniform topology.

A Remark on the Rate Function

Remark 1. The rate function I that appears in Mogulskii [1] has two misprints. This can be verified in [2]. It says

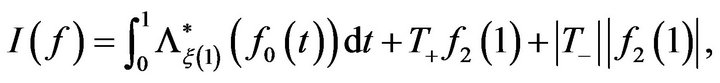
whereas it should say

Indeed, for this rate function, Mogulskii refers to the paper by Lynch and Sethuraman ([2]), and according to the latter, the value for is

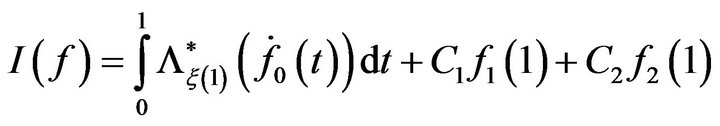
where 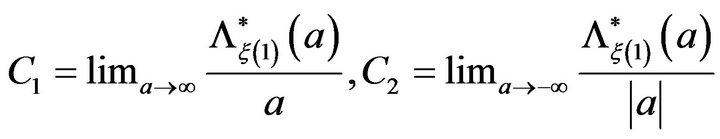and 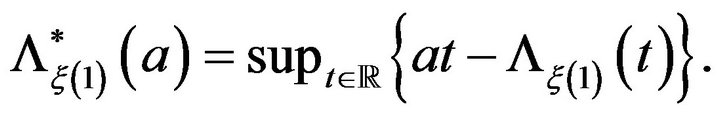Without loss of generality, suppose that 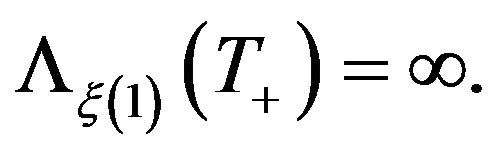Note that for

hence

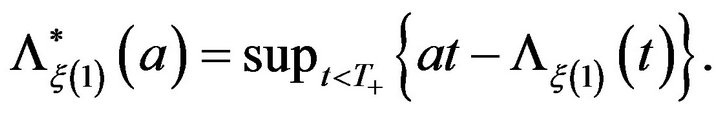
If 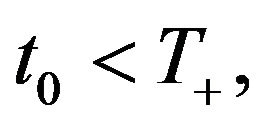then 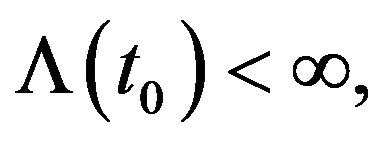and since

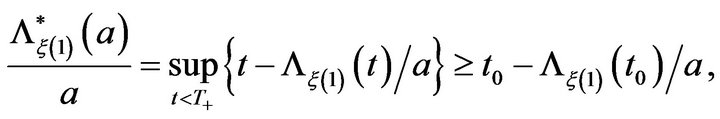
making tend to 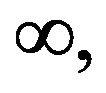we obtain

Now, if we let we conclude

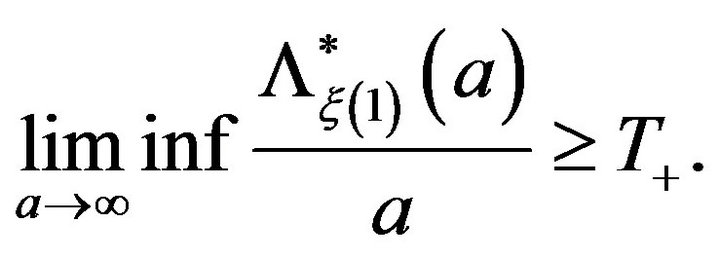(4)

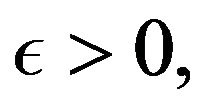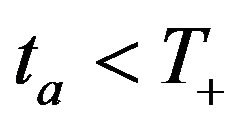On the other hand, for every and there is such that

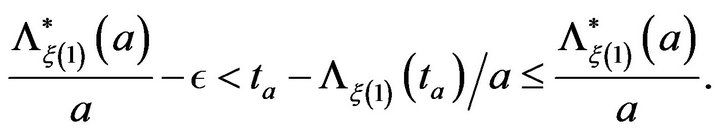
taking limits as, we conclude

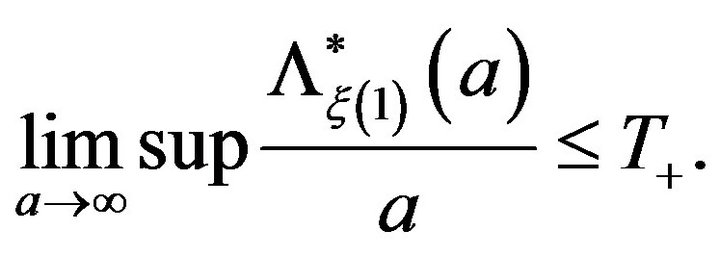(5)

In view of formulas (4) and (5) we conclude

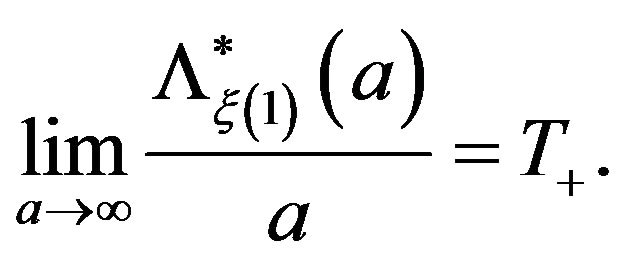
With a similar argument we obtain

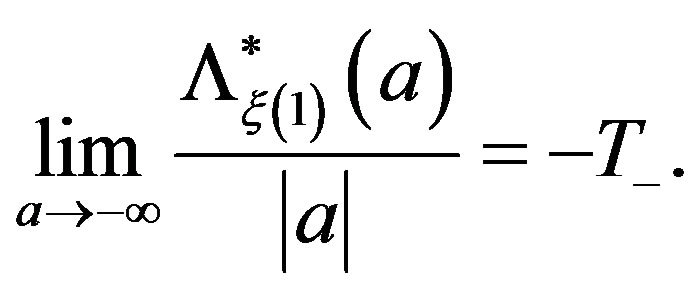
Finally, since 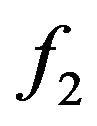is non-decreasing and

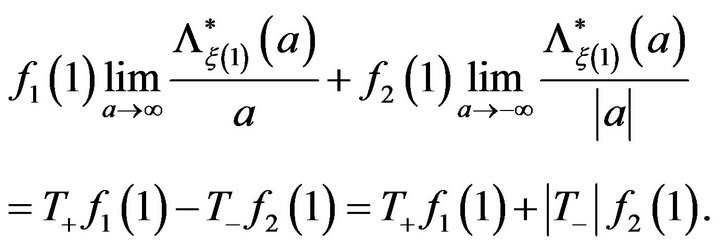
In the next Section we shall state the hypotheses we need.

3. Statement of Hypotheses

Let 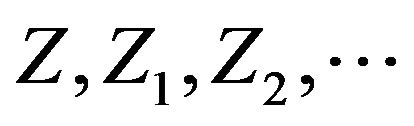be nonnegative independent and identically distributed random variables with mean and second moment (i.e. Z is non-degenerated).

Let 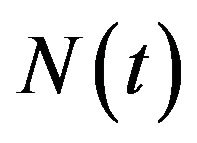be a Poisson process with parameter defined on the same probability space and independent of the 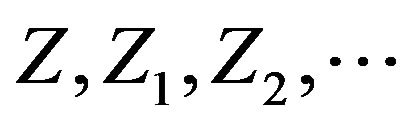All our random variables Z, and Poisson processes 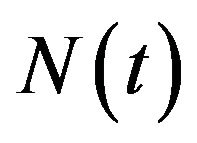will be as just stated, unless otherwise noted.

If is finite in a neighborhood of the origin, we say Condition 1 is satisfied:

Condition 1. There is 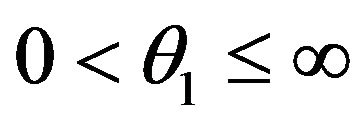such that

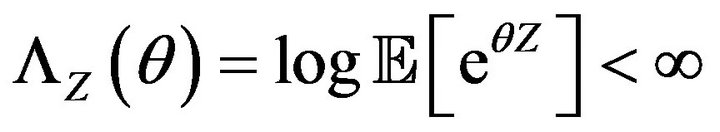for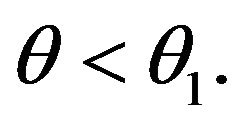

Remark 2. Finiteness of the function 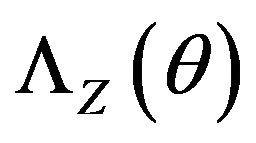is equivalent to that of the moment generating function 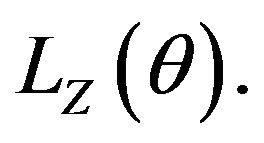Condition 1 is satisfied if 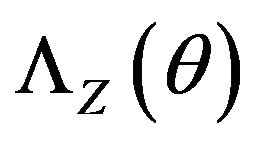is finite for some 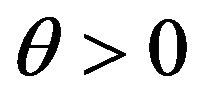(the negative part works due to Z being nonnegative).

Notice also that this condition implies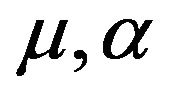, and every moment of the variables 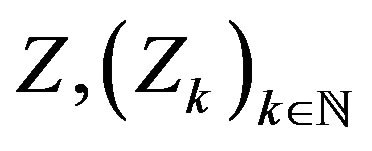are finite.

We shall fix 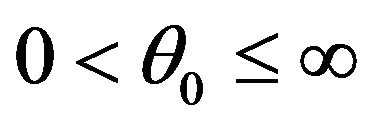to be the maximum possible by letting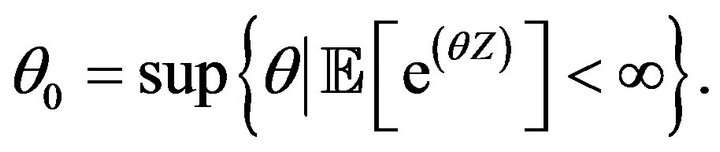

To have the LLDP in the topology we want, we require to ask an additional regularity condition:

Condition 2.

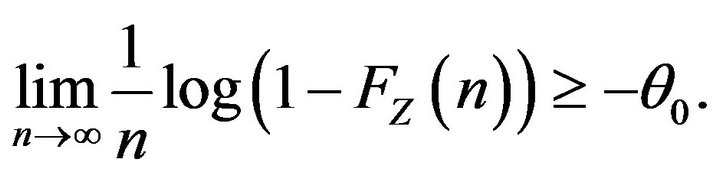
Remark 3. All the conditions on Z are satisfied if Z is, for example, exponentially distributed. This important case, for which many calculations can be made explicit, is discussed in Sections 6 and 7.

4. Large Deviations for the Risk Process on

Now we are ready to state the LDP in the space 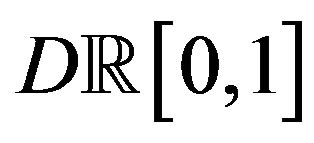with the Skorohod topology:

Theorem 1. Let 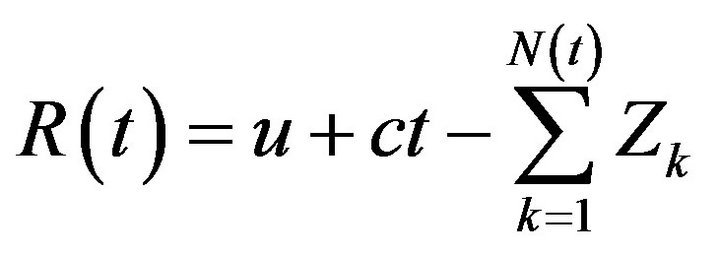be a risk process as defined in (1). Under conditions 1 and 2, the sequence of processes

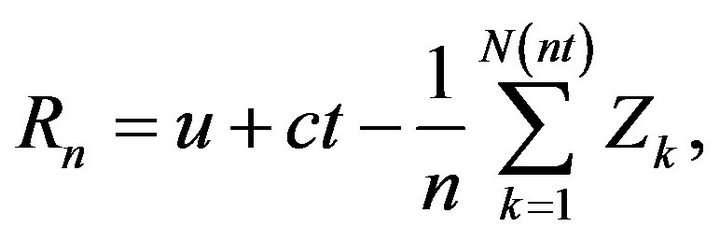(6)

satisfies the large deviations principle in the space 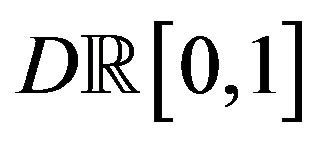with the completed topology induced by the Skorohod distance, and rate function 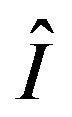defined as

(7)

where is decomposed as

and are non-decreasing.

Remark 4. The form of the rate function is given by

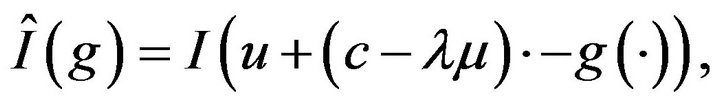(8)

with 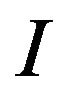as in expression (3). We also notice that, in this case,

Proof of Theorem 1.

Let 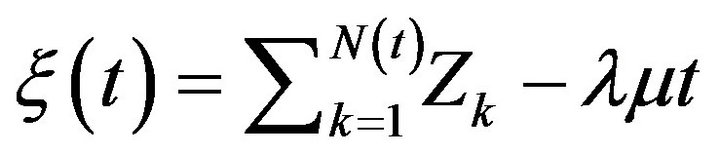be the compound Poisson process. Using the assumptions about 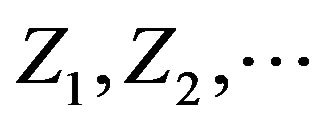and N we conclude that 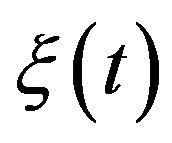has stationary and independent increments, 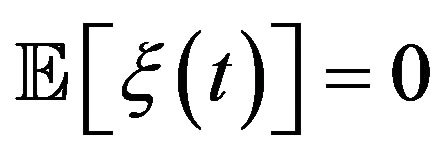and that

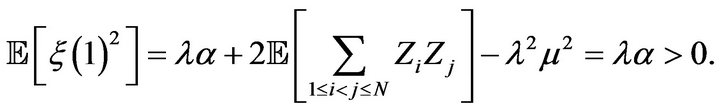
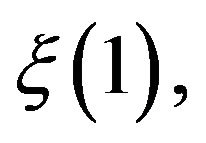The Laplace transform of is

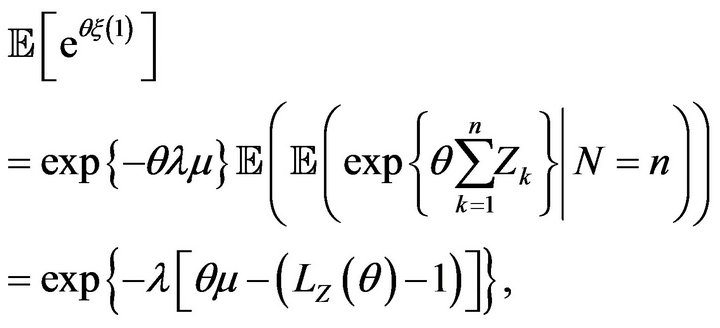
We notice that the log-Laplace

is finite as long as

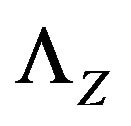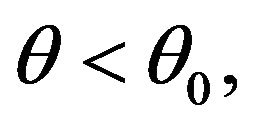is finite. By Condition 1, we can guarantee that is finite for in fact both, 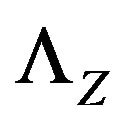and 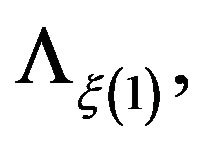have the same support. By similar calculations,

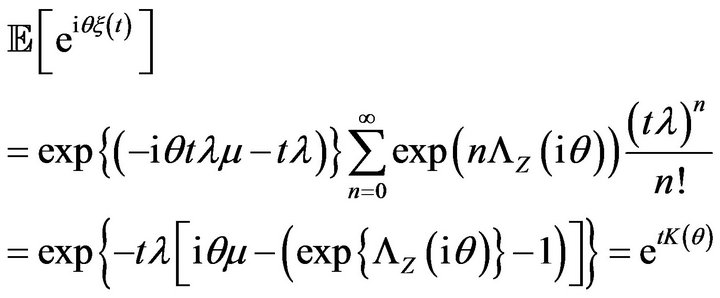
where

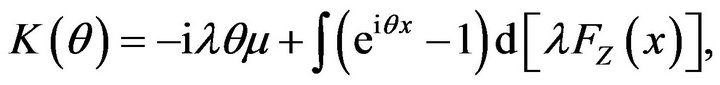
which means that the Lévy measure of this process is times the distribution of the claims. We notice that if is a sequence of sets, then

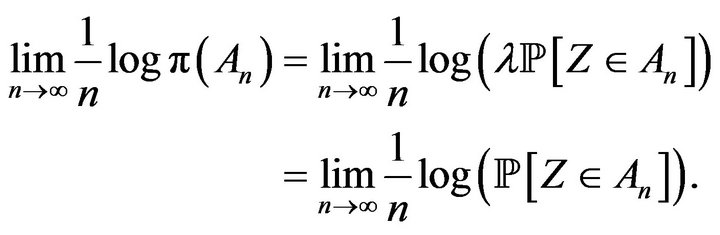
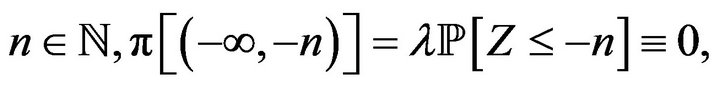Regarding the Lévy measure we see that for each therefore

and if, by the Markov inequality,

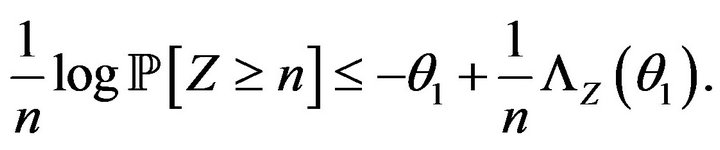
Taking the limit in the previous inequality as n approaches to, and using 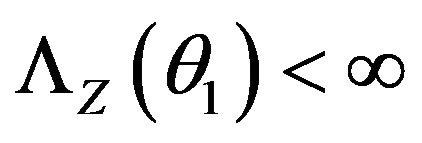gives us

and since this assertion is valid for each 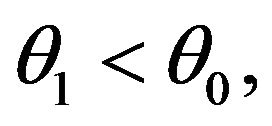we obtain

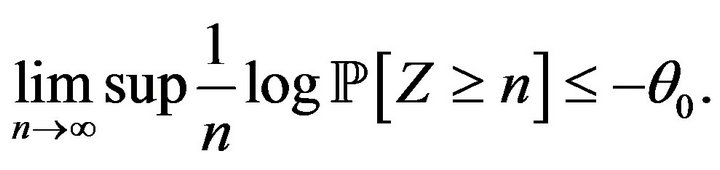
We observe that by Condition 2,

Since 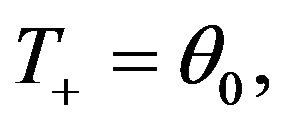we conclude that

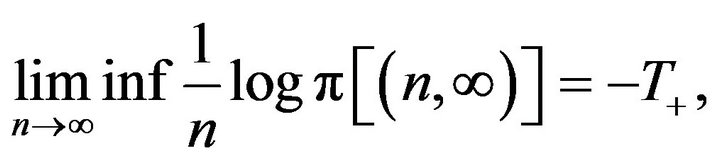
which is the regularity Condition 2. In summary, the process 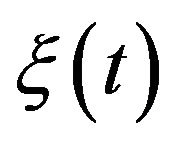satisfies the hypotheses of Proposition 1, therefore the process

satisfies the LDP with respect to the Skorohod topology with rate function provided by 3.

We now consider the metric space endowed with the completed topology induced by the Skorohod distance and we also consider the functional 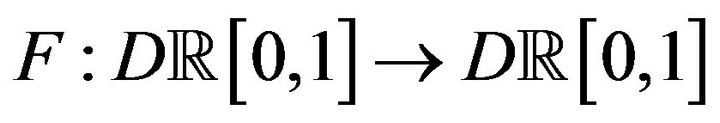defined by

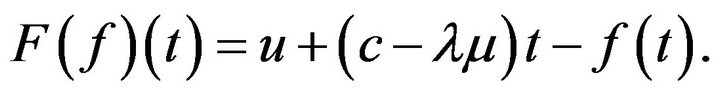
To verify continuity of F on this specific topology, take and with 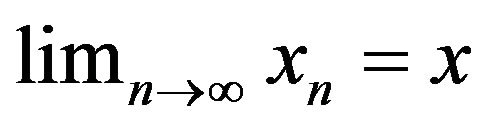in the Skorohod topology. Recall that the Skorohod distance in 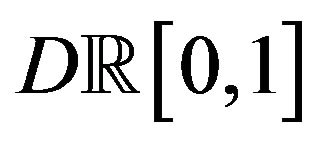is given by

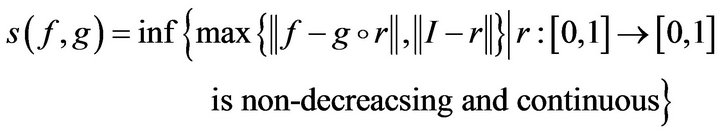
Then, there is 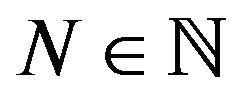so that for each we can find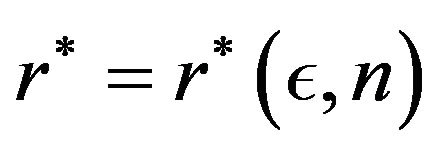, where 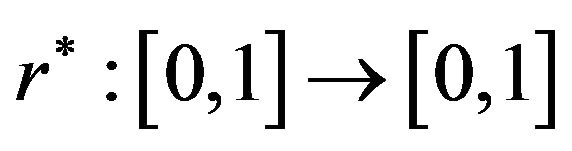is an non-decreasing continuous function for which

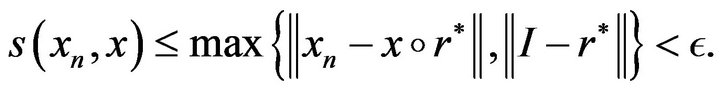
Now,

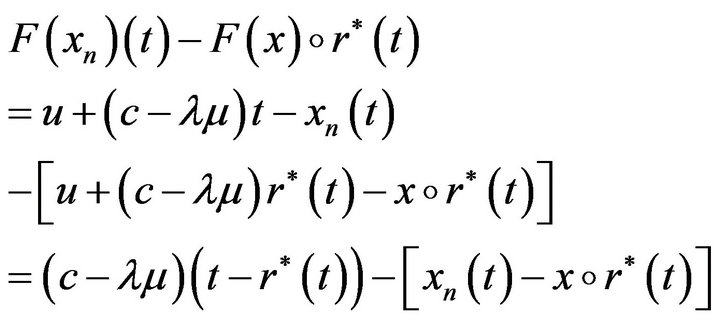
therefore

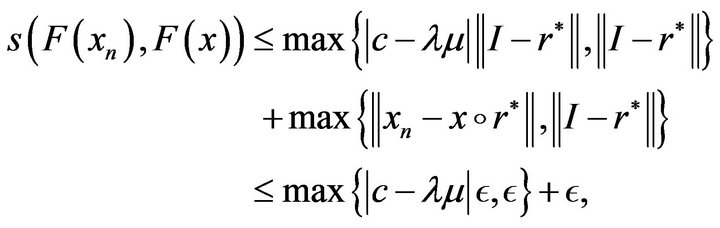
hence 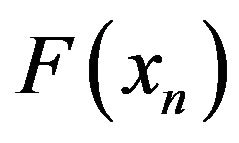tends to 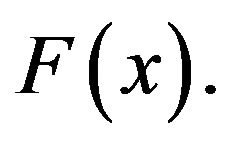Therefore F is continuous with respect to the Skorohod topology. By the Contraction Principle,

satisfies the LDP with rate function given by

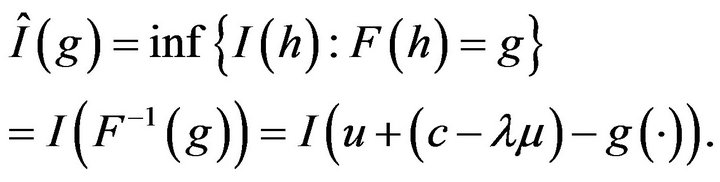
If we consider the Hahn-Jordan decomposition for 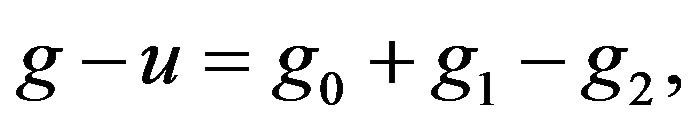and we observe that 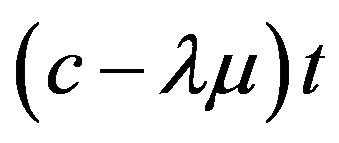is absolutely continuous with respect to the Lebesgue measure m, we conclude that the Hahn-Jordan decomposition 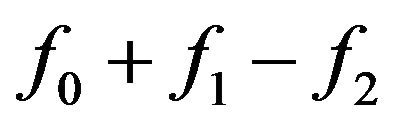for the function 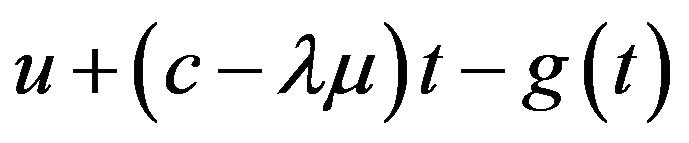is

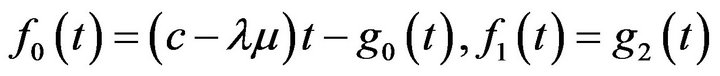, and

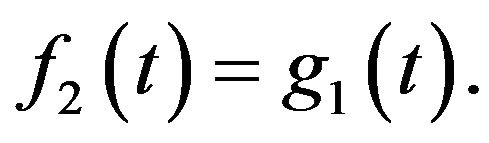Evaluating and using (3), we obtain formula (7), this concludes the proof of Theorem 1. □

5. Large Deviations for the Aggregate

Claims Process on

In this Section we prove the LDP for the process of aggregate claims, on a different space, with another time-scale parametrization, and using very different results.

Theorem 2. Assume Condition 1, but now let us denote the Poisson process as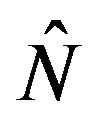, with parameter 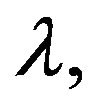defined on the same probability space and independent of the

Let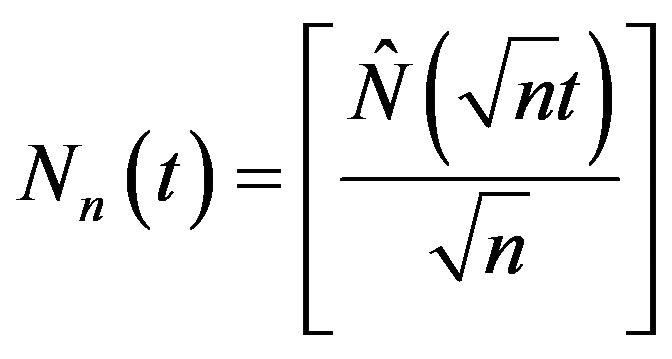. Then, the sequence of processes

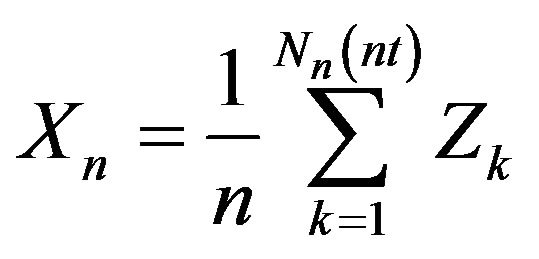
satisfies the large deviations principle in the space 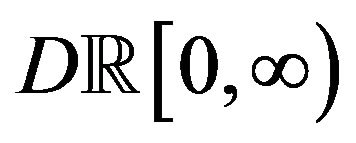with the topology induced by the Skorohod distance.

We will use results from Feng and Kurtz [9], Lemma 4.9 and Theorem 10.1, that we compile in next two Propositions:

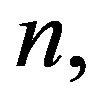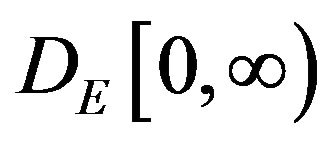Proposition 2. For each let be a process in. Let 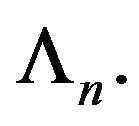be a nonnegative, nondecreasing process 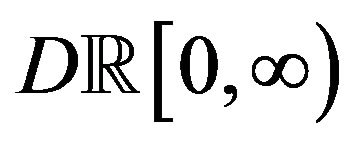valued, independent of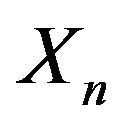. Define

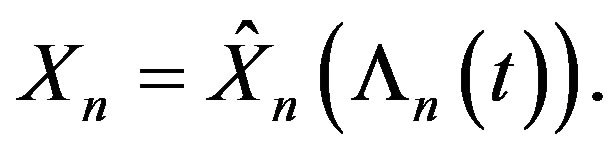
Suppose that for each 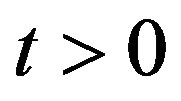and

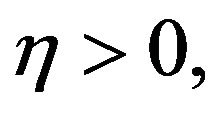
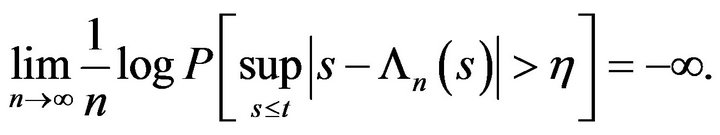(9)

If is exponentially tight, then the LDP holds for 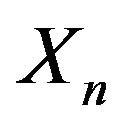if and only if it holds for.

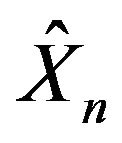Proposition 3. Let 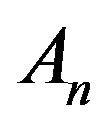be given by

for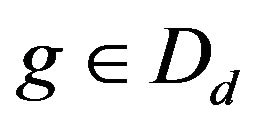. Suppose that 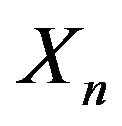is a solution of the martingale problem for 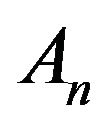and that the LDP holds for 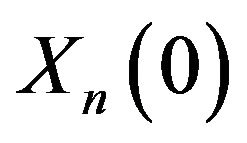in 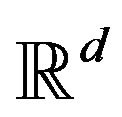with a good rate function 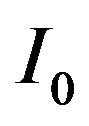and rate transform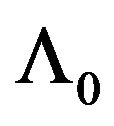. Then the LDP holds for in 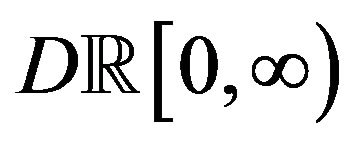with good rate function:

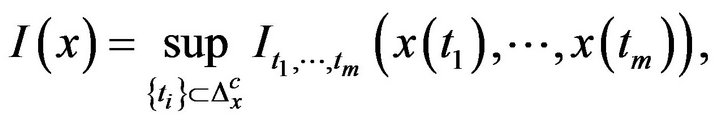(10)

where

And if 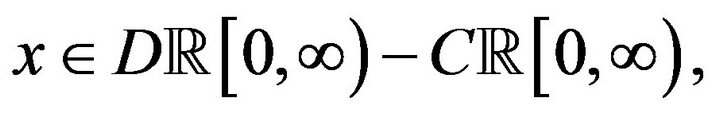then.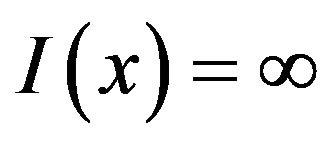

Proof of Theorem 2.

Let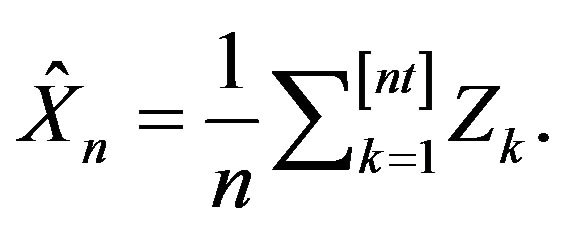

Due to the fact that 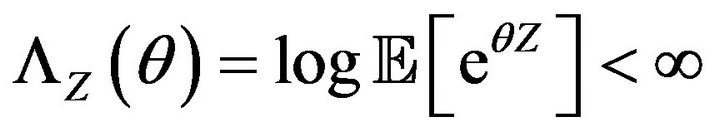for some Proposition 3 can be applied to sequences of processes with independent increments such as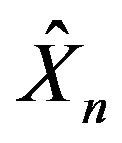—as discussed in Section 10.2 of Feng and Kurtz [9]. Therefore 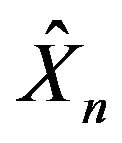satisfies the LDP with a good rate function defined as in (10). Since this rate function is good, and our space is Polish, then the sequence 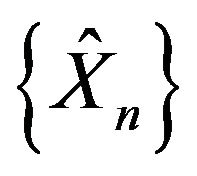is exponentially tight in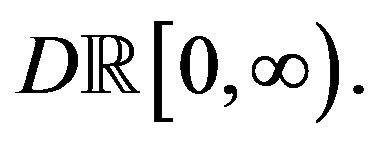

Now, let 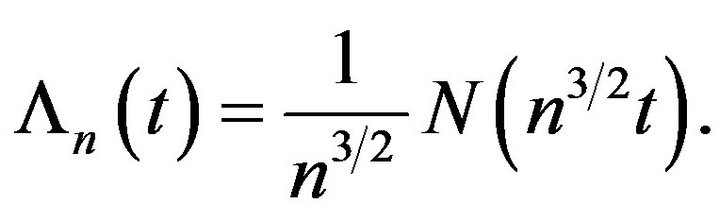By the MasonShorack, Wellner inequality [13] (p. 545) we have,

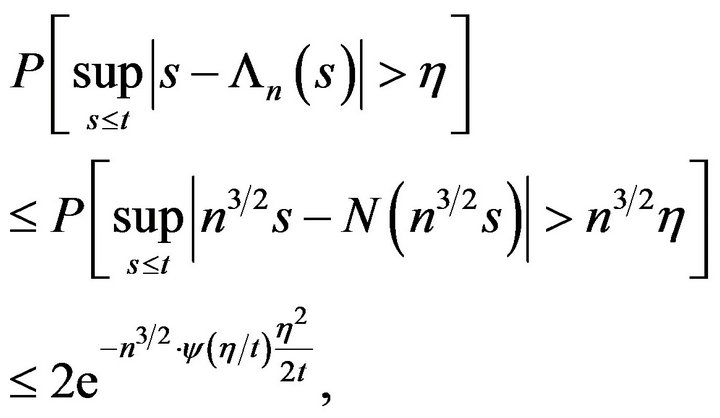
where hence

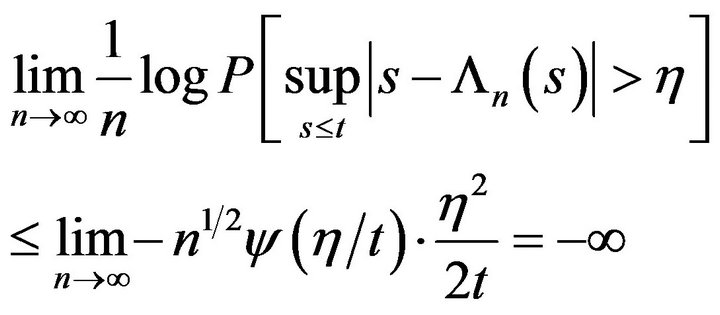
which is (9). Applying Proposition 2 we conclude that

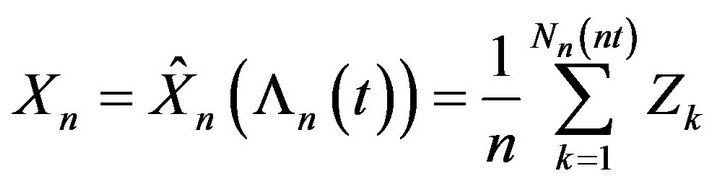
satisfies the LDP with a good rate function. □

6. Exponential Claims

In this Section we give the explicit calculations when the law of the claims is exponential, and we also find the particular shape for the rate function. We have the following Corollary to Theorem 1:

Corollary 1. Consider a classical risk process as defined in (1) with exponentially distributed claims:

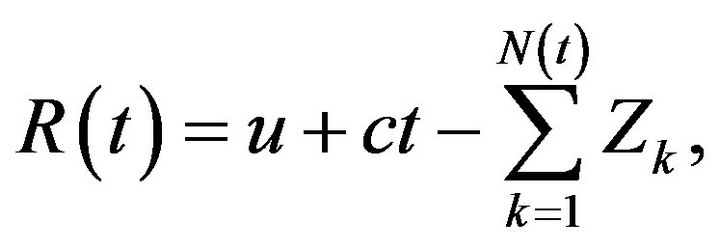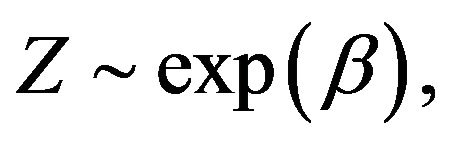with and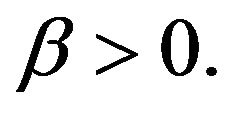

The sequence of processes

(11)

satisfies the LDP in the space 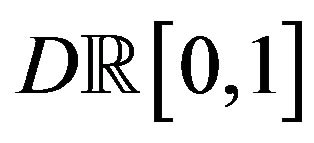with the completed topology induced by the Skorohod distance, and rate function given by

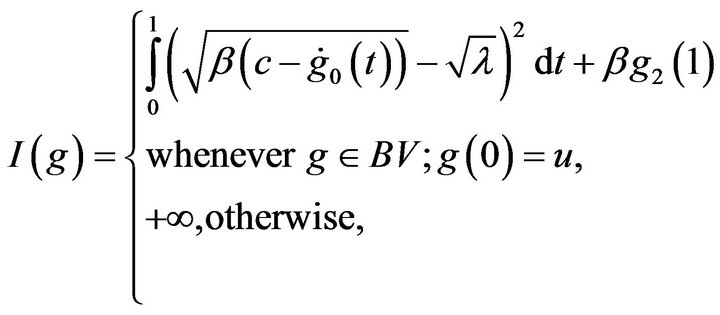(12)

with

non-decreasing, and.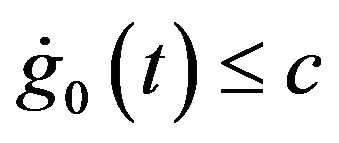

Proof. The Moment Generating function in this case is

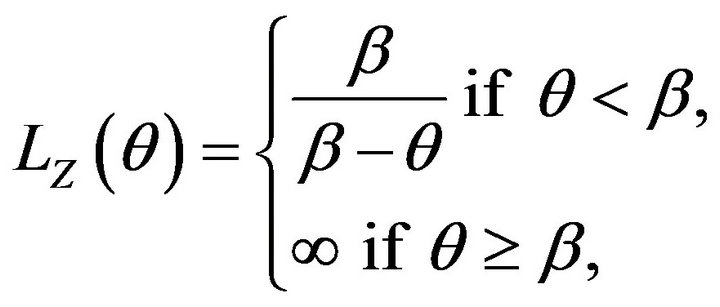
hence 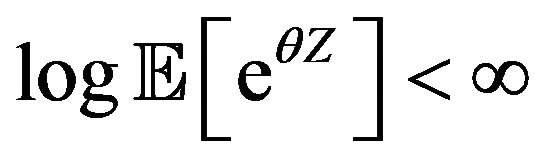if and only if 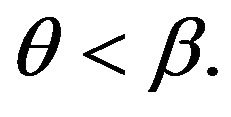Therefore, Condition 1 holds. In this case

Also,

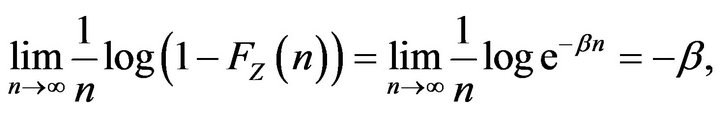
so Condition 2 also holds.

Applying Theorem 1, we conclude that satisfies the LDP with rate function given by (7). It remains to show that the rate function has the explicit form (12). Let us calculate, for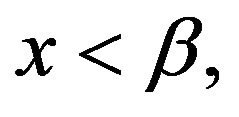

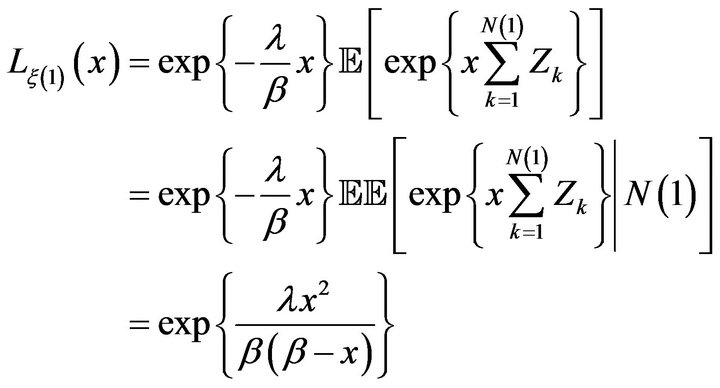
Now

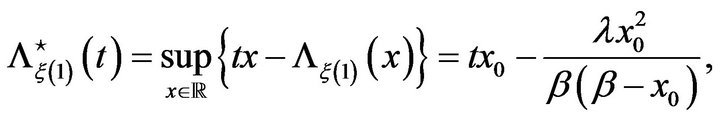
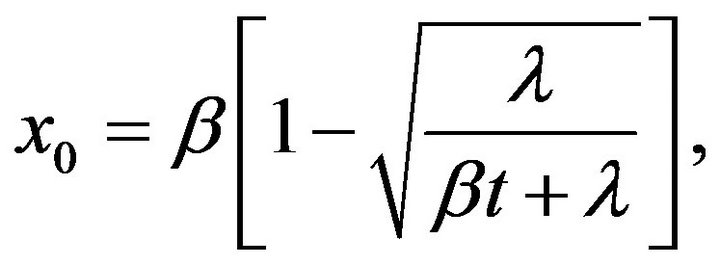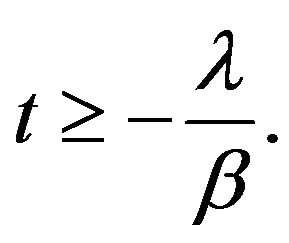with if Therefore,

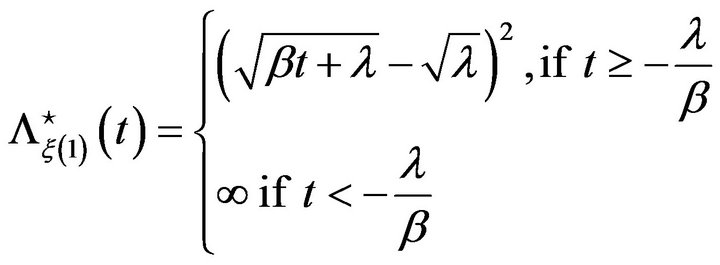(13)

Here, again the Hahn-Jordan decomposition

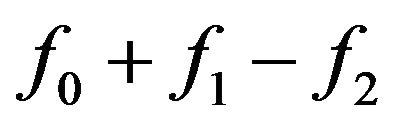for the function is

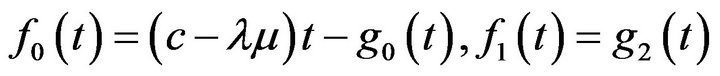, and

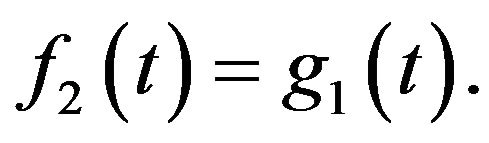Therefore,

provided 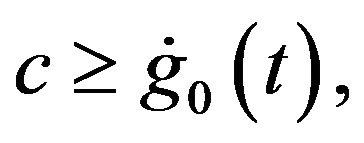(otherwise).

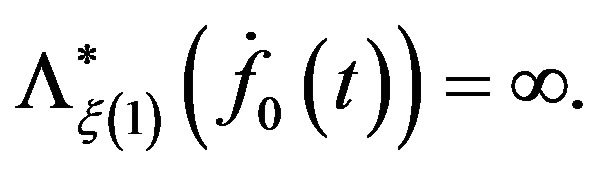Since 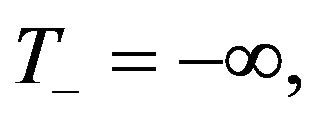the value

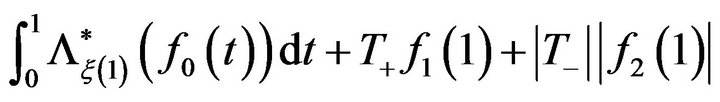in the rate function (7) provides us information only when 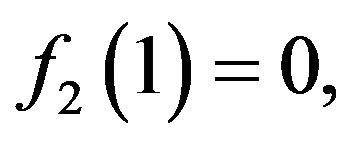and since 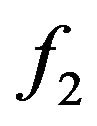is non-decreasing and 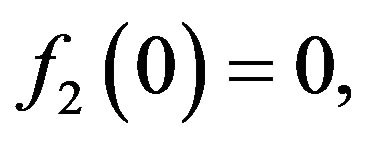this implies that 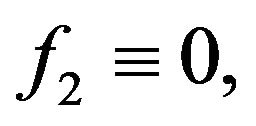in our case Finally, 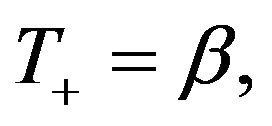hence the rate function 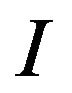takes the form (12). This proves Corollary 1. □

7. Estimating the Ruin Probability of the Process R_n

In this section we give an upper bound for the Probability of Ruin for the process as studied in Section 6 and in Corollary 1; i.e. when the claims are exponentially distributed with parameter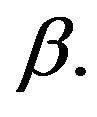

Theorem 3. For the process 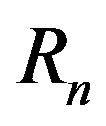defined in Corollary 1, we have that

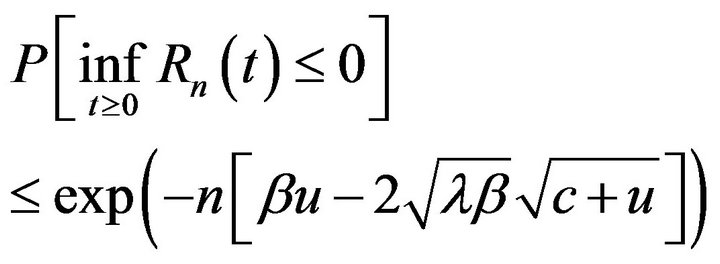(14)

for sufficiently large n. The estimate is meaningful when

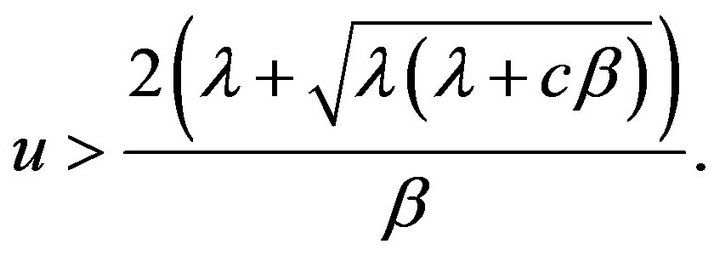(15)

Proof of Theorem 3.

By Corollary 1, satisfies the LDP with good rate function given by (12), therefore

for some function 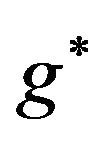in the essential domain of 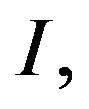hence 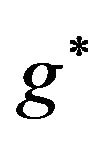satisfies:

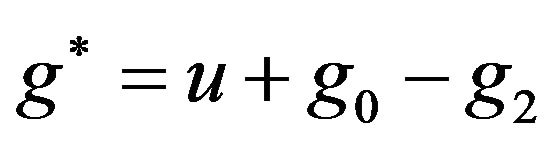where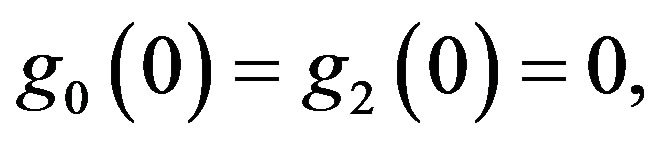

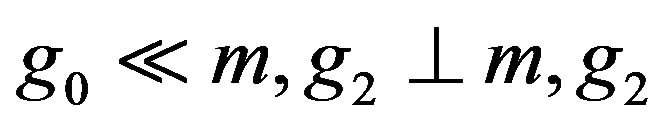non-decreasing, there is a first time when

By definition of we have

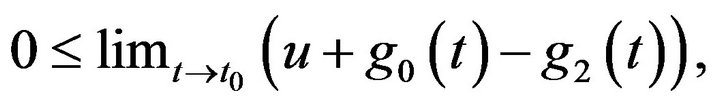since 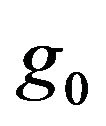is continuous and 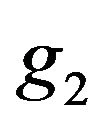is non-decreasing, we conclude that

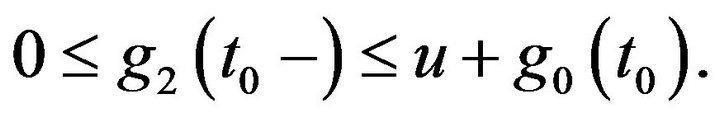
Therefore

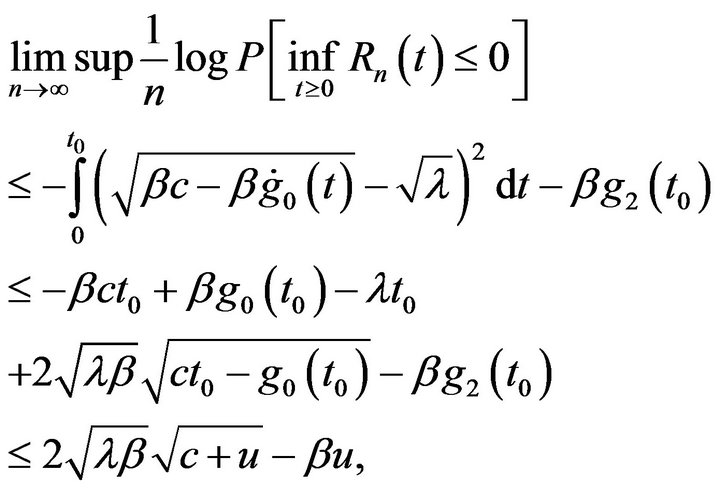
the second inequality is due to Jensen’s inequality. Note that 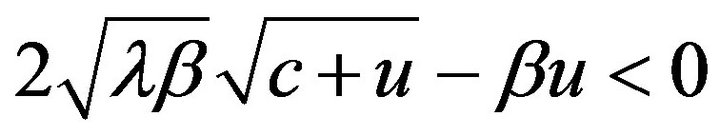if and only if is above the largest root of the polynomial 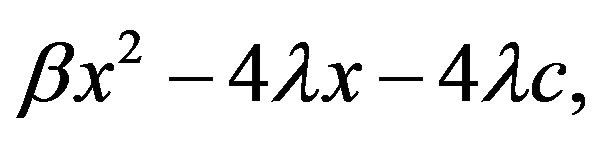such root is precisely the right hand side of inequality (15). This proves Theorem 3. □

Remark 5. The estimate of the probability ruin provided here for the process 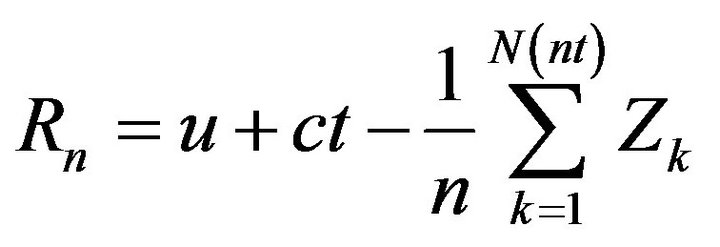is, whereas the exact probability of ruin for the process (seefor instance, Section 1.2 of [14]) is

  Note that the exponent in our estimation also behaves as a polynomial on of first degree when is large.

If the claims are not exponentially distributed, we can still make the following observation regarding the probability of ruin.

Corollary 2. Consider the rate function for the process in Theorem 1, 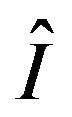, and let be the dominating point of

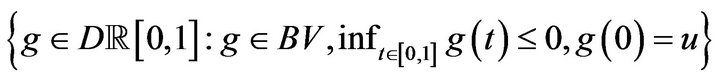with respect to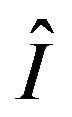. Consider also the decomposition

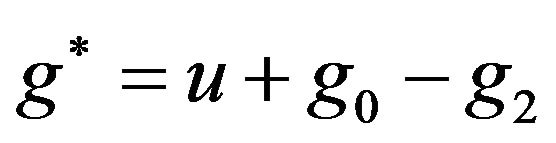, where

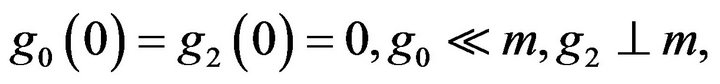and with 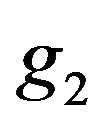nondecreasing.

If 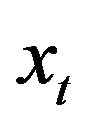is a solution of

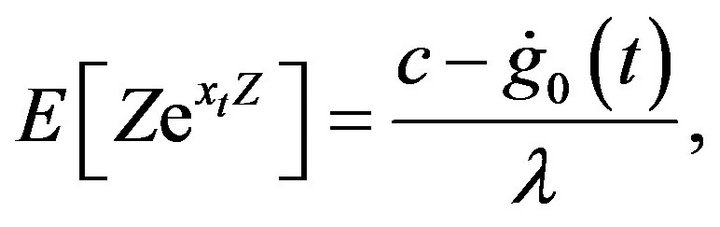(16)

then, for the process 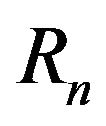defined in (6), we have

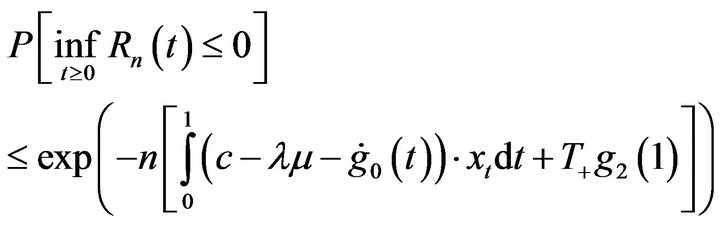(17)

for sufficiently large n.

Recall that the LDP proved in Theorem 1 holds for claims with moment generating functions much less restrictive than the super-exponential case.

Proof of Corollary 2. By Corollary 1, 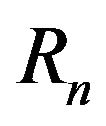satisfies the LDP with good rate function 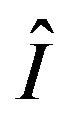given by (7), therefore

where the function is as in the statement above.

Since

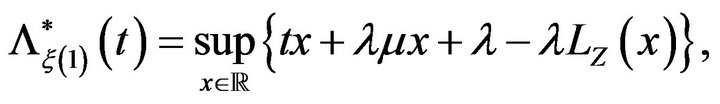
and since 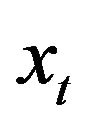is as in (16), then

Finally,

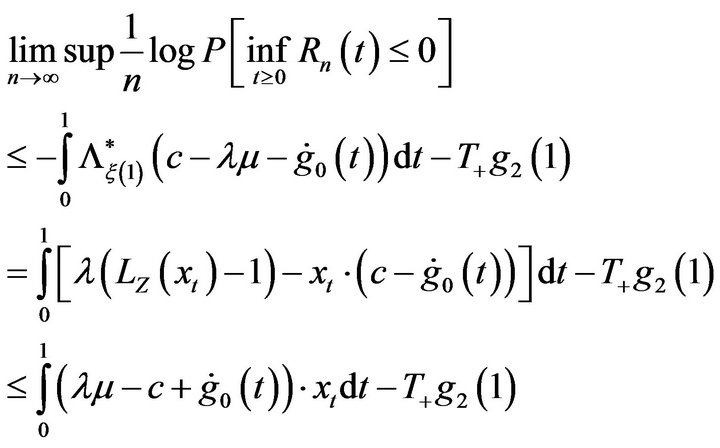
For the second inequality we used the fact that □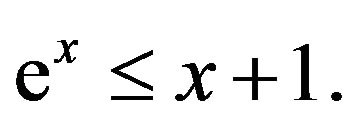

8. Acknowledgements

We would like to thank both our universities CSUCI and UNAM, for their hospitality while doing this joint work.

REFERENCES

NOTES

^*This work was partially supported by Projects PAPIIT—IN103606, IN117109 DGAPA—UNAM, and PAEP—2008, 2009—UNAM.