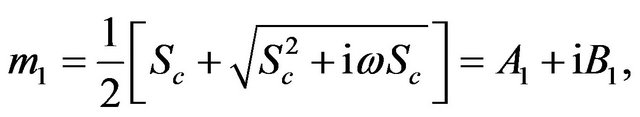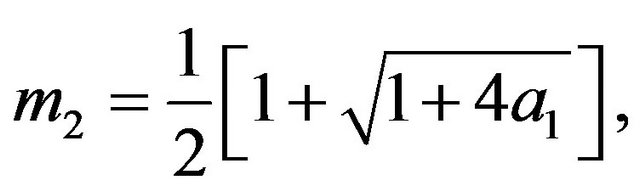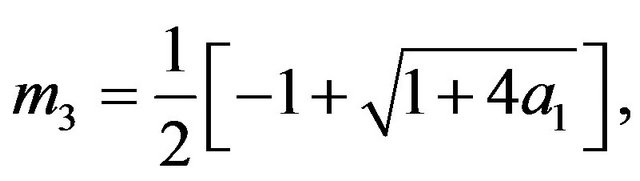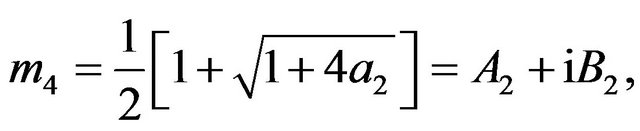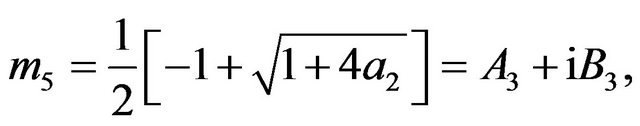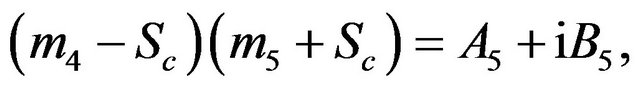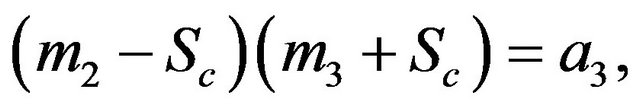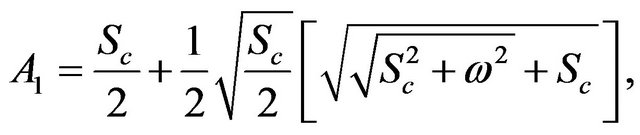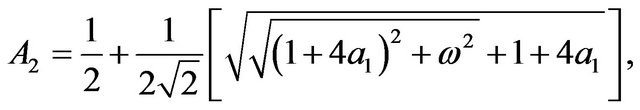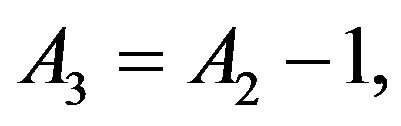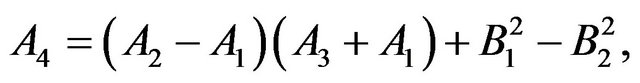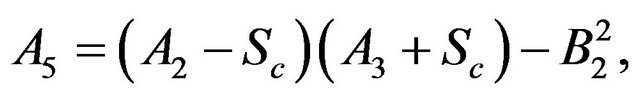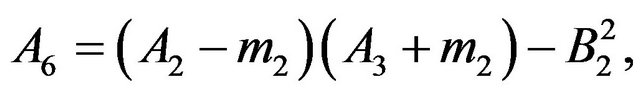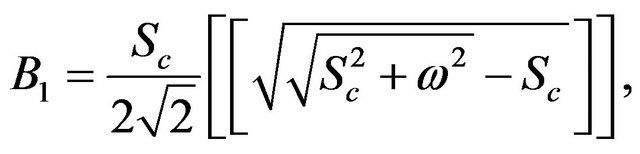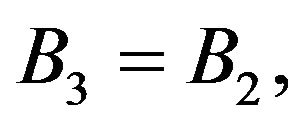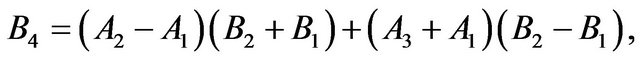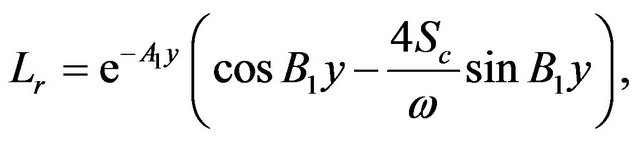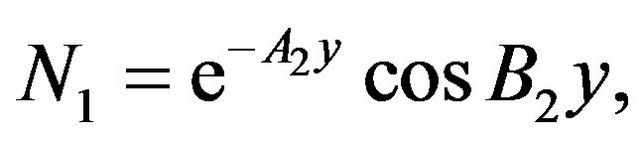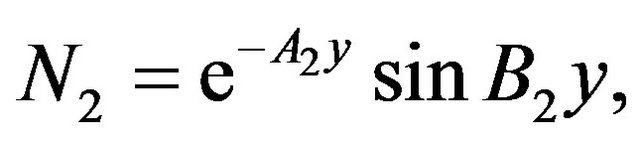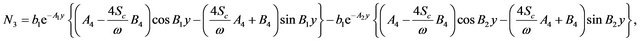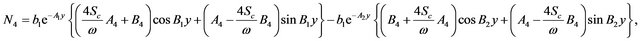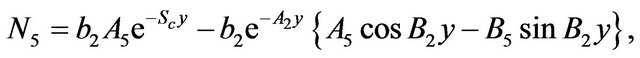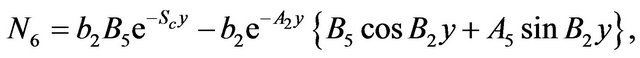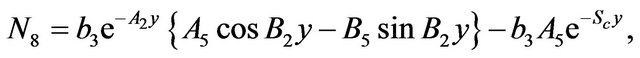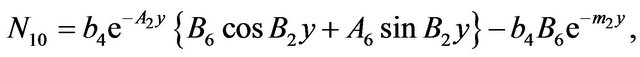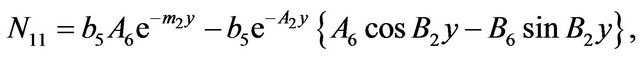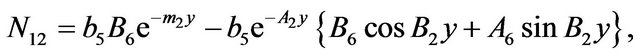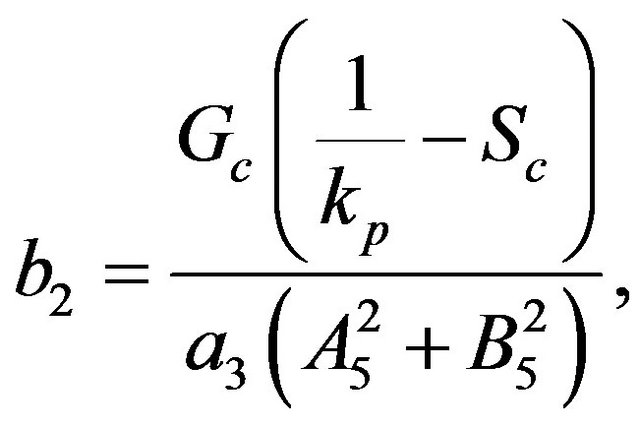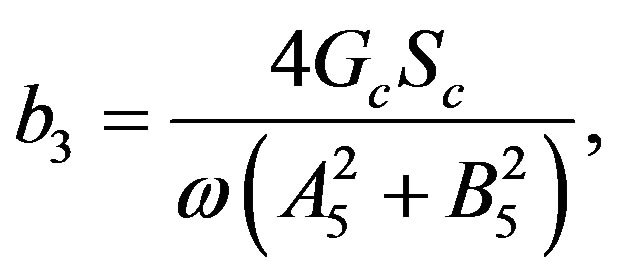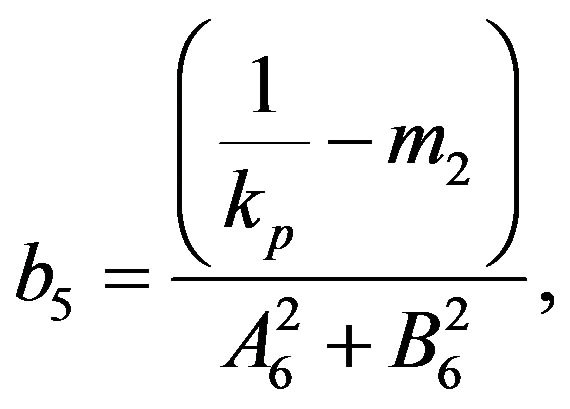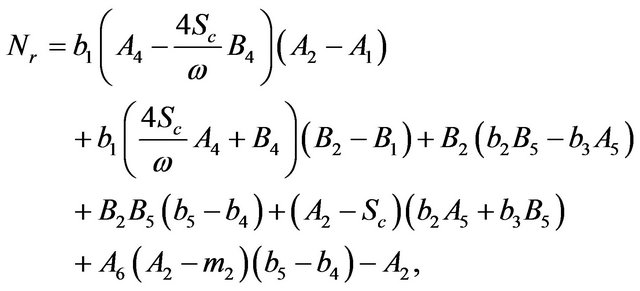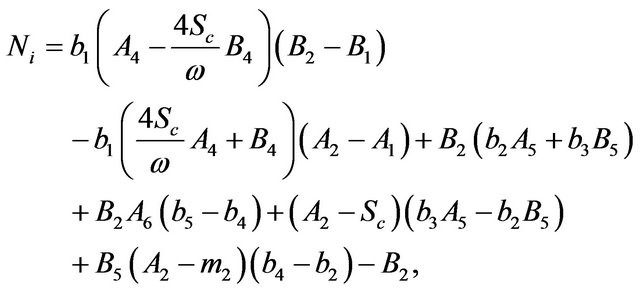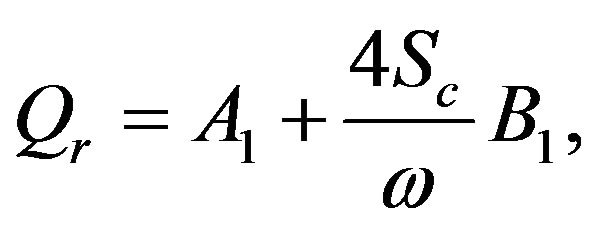Applied Mathematics
Vol.4 No.4(2013), Article ID:30741,9 pages DOI:10.4236/am.2013.44096
Solution of MHD Flow past a Vertical Porous Plate through a Porous Medium under Oscillatory Suction
1University College in Al-Jamoum, Umm Al-Qura University, Mecca, KSA
2Akhbar El-Yom Academy, Giza, Egypt
Email: a_saltah@hotmail.com, ha_ssanin@yahoo.co
Copyright © 2013 Ashraf A. Moniem, W. S. Hassanin. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 22, 2012; revised February 21, 2013; accepted February 28, 2013
Keywords: MHD Flow; Mass Transfer; Porosity; Oscillation Suction
ABSTRACT
The model of mass transfer on free convective flow of a viscous incompressible electrically conducting fluid past vertically porous plate through a porous medium with time dependant permeability and oscillatory suction in presence of a transverse magnetic field is considered. Perturbation technique is obtained the solution for velocity field and concentration distribution analytically. The effects of the flow parameters on the velocity field and concentration distribution are presented with the aid of figures. Also, the skin friction and the rate of mass transfer are calculated with the aid of tables.
1. Introduction
The phenomena of MHD flow with unsteady oscillatory free convective flows play an important role in aerospace technology and in chemical engineering turbo-machinery. Such flow arise either due to unsteady motion of boundary or due to oscillatory free system velocity. Several authors have studied the free convection and mass transfer flow of a viscous fluid through porous medium. They considered that, the permeability of the porous medium is assumed to be constant, while the porosity of the medium may be not necessary constant because the porous material containing the fluid is non-homogenous medium. Then, the permeability of the porous medium may be not necessary constant. The effect of mass transfer on free convective hydromagnetic oscillatory flow past an infinite vertical unsteady flow of non-Newtonian fluid has been estimated by Koullias et al. [1]. Ashgar et al. [2] have reported the periodic unsteady flows of non-Newtonian fluid. The flow of non-Newtonian fluid induced due to the oscillations of a porous plate has studied by Hayat et al. [3]. Singh and Gupta [4] have investigated the MHD free convective flow of a viscous fluid through a porous medium bounded by an oscillating porous plate in the slip flow regime with mass transfer. Das et al. [5] analyzed the mass transfer effects on unsteady flow past an accelerated vertical porous plate with suction employing numerical methods. Raptis [6] analyzed the unsteady free convection flow through a porous medium. Hossain and Begum [7] discussed the effect of mass transfer and free convection on the flow past a vertical plate. Unsteady hydromagnetic convective flow past an infinite vertical porous flat plate in a porous medium has been discussed by Das and his coworkers [8]. The objective of the present study is to analyzed the effects of permeability variation and oscillatory suction velocity in free convective and mass transfer flow of a viscous incompressible fluid past an infinite vertical porous plate through a porous medium when the plate is subjected to a time dependent suction velocity normal to the plate in the presence of a uniform transverse magnetic field. The solutions for velocity field and concentration distribution are obtained by perturbation technique analytically. The effects of the flow parameters on the velocity field and concentration distribution are presented with the aid of figures. Also, the skin friction and the rate of mass transfer are calculated with the aid of tables.
2. Mathematical Analysis
The unsteady free convective flow of a viscous incompressible electrically conducting fluid past an infinite vertical porous plate through a porous medium with time dependant permeability and oscillatory suction in presence of a transverse magnetic field is considered. The y-axis is taken along the infinite vertical porous plate and x-axis is perpendicular to it and the velocity in this direction is u. In view of these, the analysis of the problem is based on the following assumptions:
• All the fluid properties are constant;
• The plate as well as the fluid is assumed to be at the same temperature and the concentration of the species is raised or lowered;
• The magnetic Reynolds number is small so that the induced magnetic field can be neglected in comparison to the applied magnetic field;
• The permeability of the porous medium is assumed to be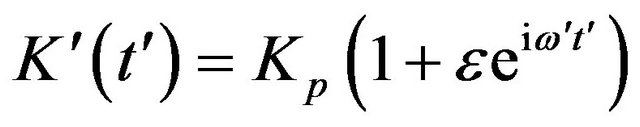 ;
;
• The suction velocity is assumed to be 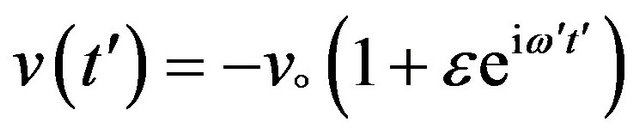 .
.
With foregoing assumptions and taking the usual Boussinesq’s approximation into account as well as following non-dimensional quantities:
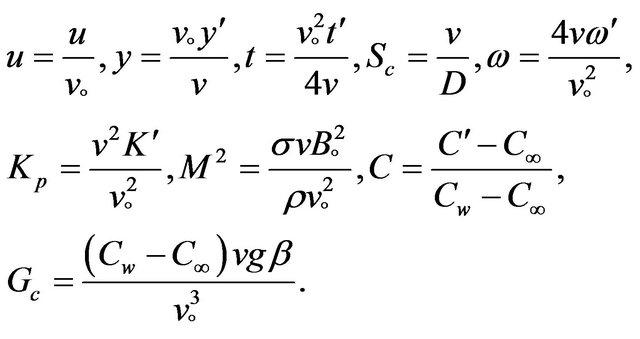 (1)
(1)
Therefore, the non-dimensional form of the governing equations for momentum and concentration are:
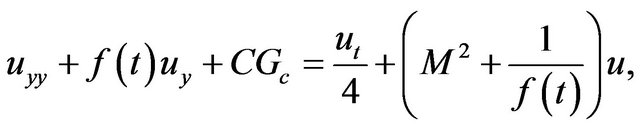 (2)
(2)
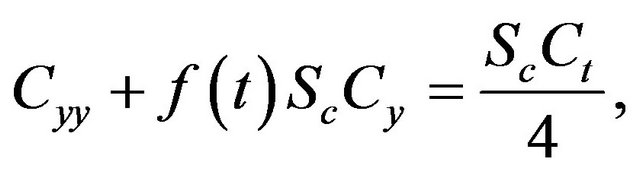 (3)
(3)
where 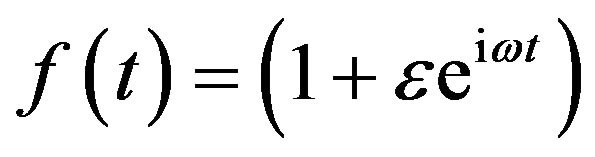 Subjected to the following boundary conditions:
Subjected to the following boundary conditions:
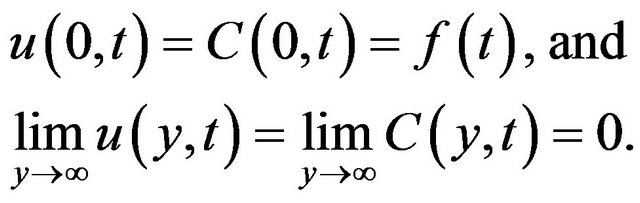 (4)
(4)
3. Solutions of the Problem
In order to solve the problem, we assume the solutions of the following form because the amplitude 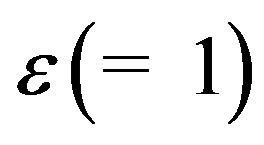 of the permeability variation is very small:
of the permeability variation is very small:
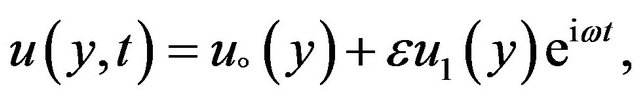 (5)
(5)
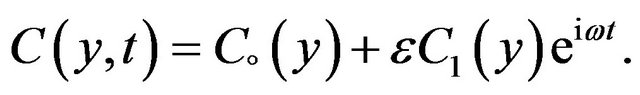 (6)
(6)
Substitute Equations (5) and (6) into Equations (2) and (3) and equate the harmonic and non-harmonic terms to obtain the following non-dimensional ordinary differential equations:
 (7)
(7)
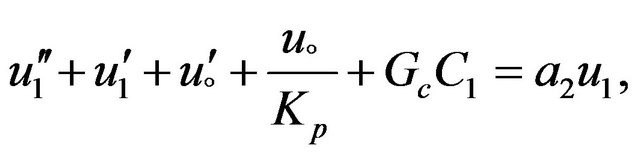 (8)
(8)
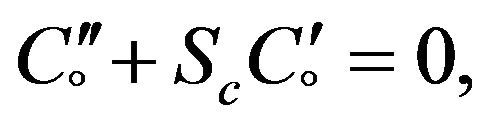 (9)
(9)
 (10)
(10)
where 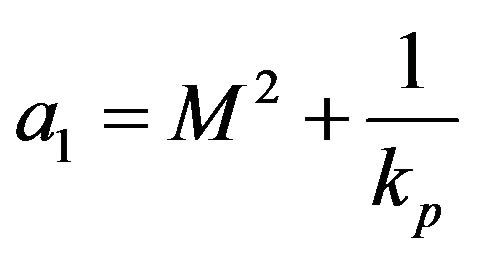 and
and .
.
Furthermore, the boundary conditions are reduced to
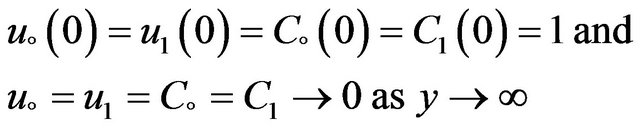 (11)
(11)
By solving Equations (7)-(10) under boundary conditions (11), we obtain
 (12)
(12)
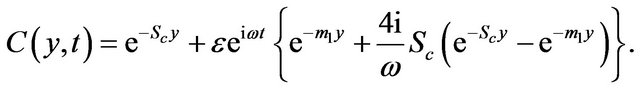 (13)
(13)
The real and imaginary parts are separated from Equations (12) and (13). The physical significance is the real parts which are given as follow:
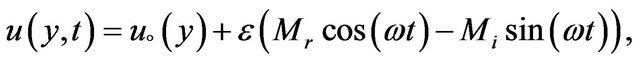 (14)
(14)
 (15)
(15)
For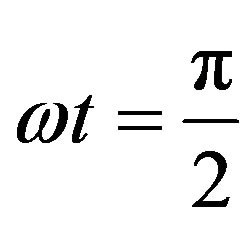 , the transient velocity and concentration distribution are given by
, the transient velocity and concentration distribution are given by
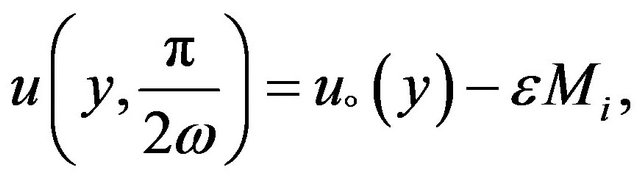 (16)
(16)
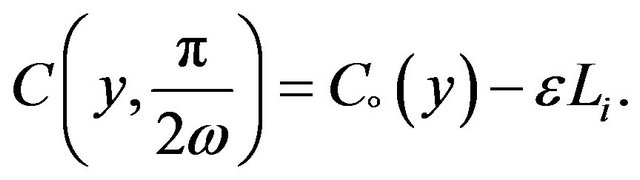 (17)
(17)
The skin friction at the plate in terms of amplitude and phase is given by
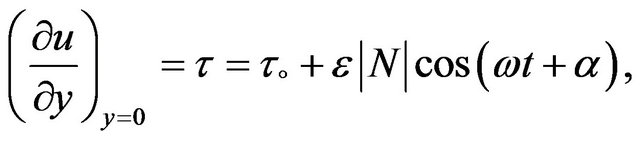 (18)
(18)
where
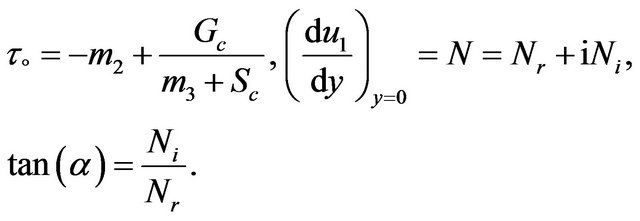 (19)
(19)
The Sherwood number (the mass transfer coefficient) at the plate terms of amplitude and phase is given by
 (20)
(20)
where
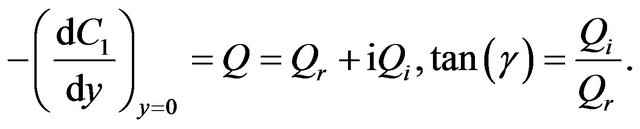 (21)
(21)
The constants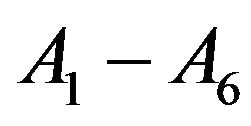 ,
,  ,
, 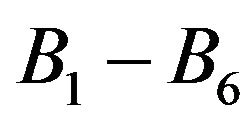 ,
, 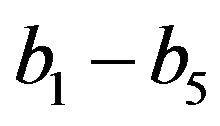 ,
, 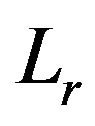 ,
, 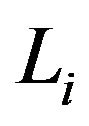 ,
, 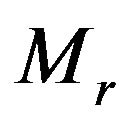 ,
, 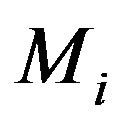 ,
, 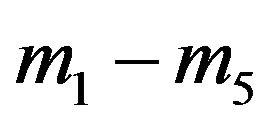 ,
, 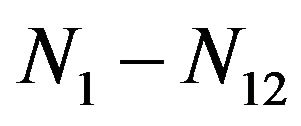 ,
, 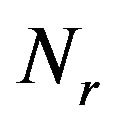 ,
,  ,
, 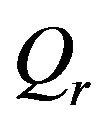 ,
, 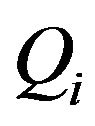 ,
, 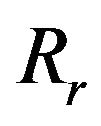 and
and 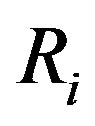 are defined in appendix section.
are defined in appendix section.
4. Numerical Simulation and Discussion
The problem of free convective and mass transfer flow of a viscous incompressible electrically conducting fluid past an infinite vertical porous plate through a porous medium when with time dependent permeability and oscillatory suction in presence of a uniform transverse magnetic field has been considered. Perturbation technique is obtained the solution for velocity field and concentration distribution analytically. The effects of the flow parameters such as magnetic parameter M, Grashof number for mass transfer Gc porosity parameter Kp and Schmidt number Sc have been studied analytically and presented with the help of Figures 1-4, respectively. The effects of Schmidt number Sc on the concentration distribution have been showed in Figure 5. Furthermore, the effects of the flow parameters on skin friction and the rate of mass transfer have been reported with the help of Tables 1-7.
The effect of magnetic field parameter M on the velocity profiles of the flow field keeping other parameters of the flow field constant is showed in Figure 1. The magnetic field parameter is taken in increasing order and it is found to slow down the velocity of the flow field to a considerable amount due to the magnetic pull of the Lorentz force acting on the flow field. This parameter shows overturn effect.
The effect of Schmidt number Sc on the velocity profiles of the flow field keeping other parameters of the flow field constant is showed in Figure 2. The Schmidt number is taken in increasing order and it is reveal that the presence of heavier diffusion species has a delaying effect on velocity of the flow field. This parameter shows reverse effect.
The effect of Grashof number for mass transfer Gc on the velocity profiles of the flow field keeping other parameters of the flow field constant is showed in Figure 3. It is noted that the Grashof number for mass transfer is accelerated the velocity of the flow field at all points.
The effect of porosity parameter Kp on the velocity
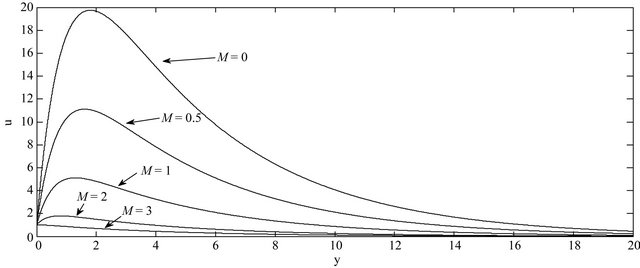
Figure 1. Effect of M on velocity profiles with ,
, 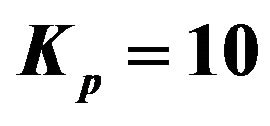 ,
, 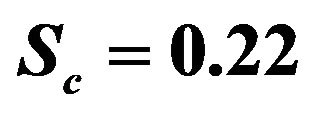 ,
, 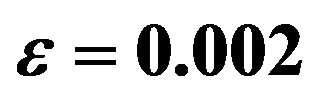 ,
, 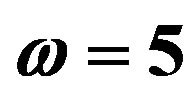 and
and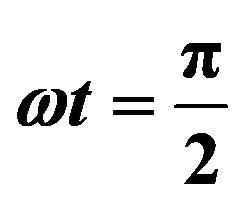 .
.
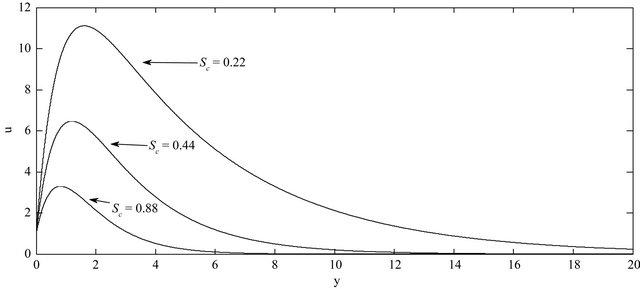
Figure 2. Effect of Sc on velocity profiles with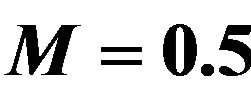 ,
, 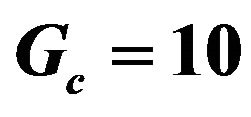 ,
, 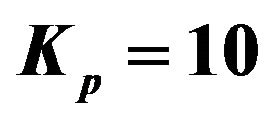 ,
, 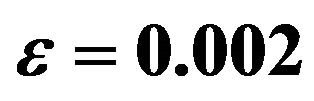 ,
, 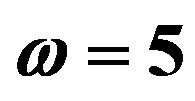 and
and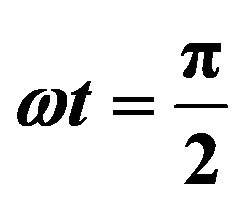 .
.
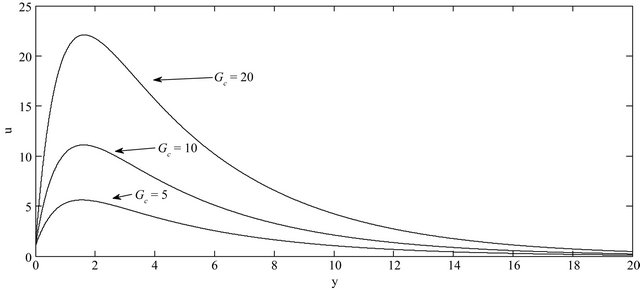
Figure 3. Effect of Gc on velocity profiles with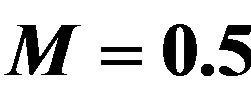 ,
, 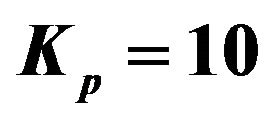 ,
, 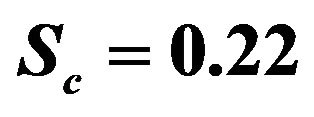 ,
, 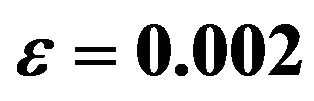 ,
,  and
and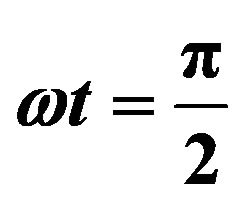 .
.
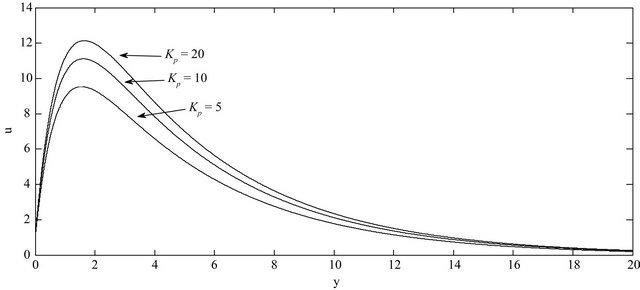
Figure 4. Effect of Kp on velocity profiles with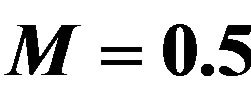 ,
, 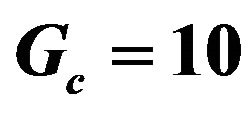 ,
, 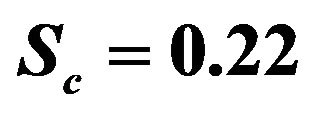 ,
, 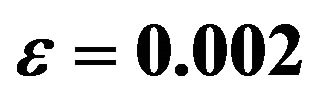 ,
, 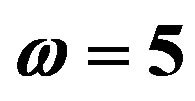 and
and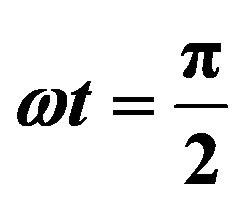 .
.
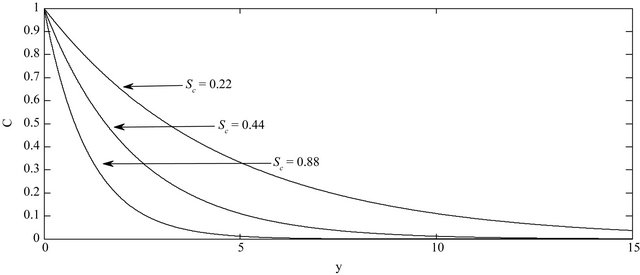
Figure 5. Effect of Sc on concentration distribution with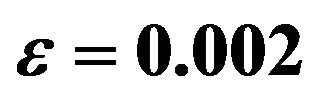 ,
, 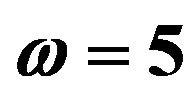 and
and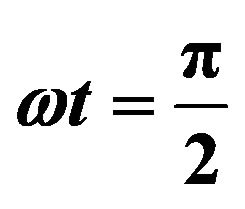 .
.
Table 1. Values of amplitude, phase and the skin friction coefficients for different values of M with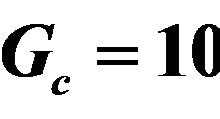 ,
, 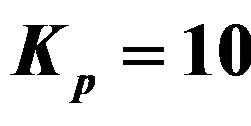 ,
, 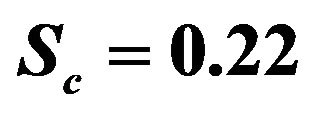 ,
, 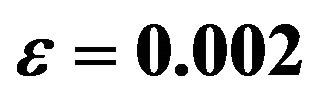 ,
, 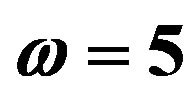 and
and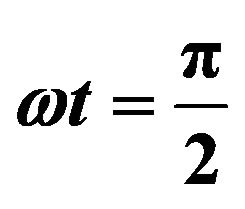 .
.
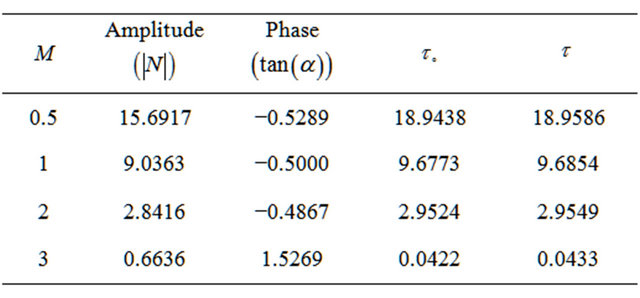
Table 2. Values of amplitude, phase and the skin friction coefficients for different values of Sc with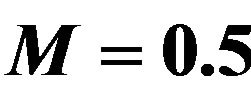 ,
,  ,
,  ,
,  ,
, 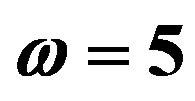 and
and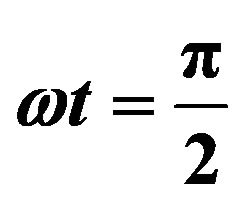 .
.

profiles of the flow field keeping other parameters of the flow field constant is showed in Figure 4. It is observed that the porosity parameter is enhanced the velocity of the flow field at all points.
The concentration distribution decreases at all points of the flow field with the increase of the Schmidt number Sc. Singh et al. [9] have applied this result into some foreign mass such as hydrogen (Sc = 0.22) helium (Sc = 0.30) and ammonia (Sc = 0.78).
Table 3. Values of amplitude, phase and the skin friction coefficients for different values of Gc with ,
, 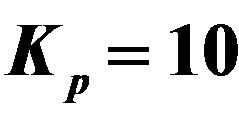 ,
, 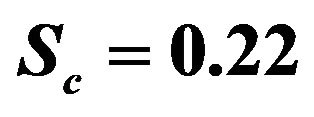 ,
, 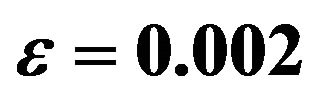 ,
, 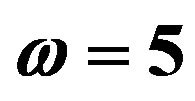 and
and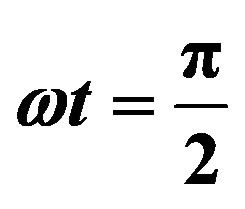 .
.
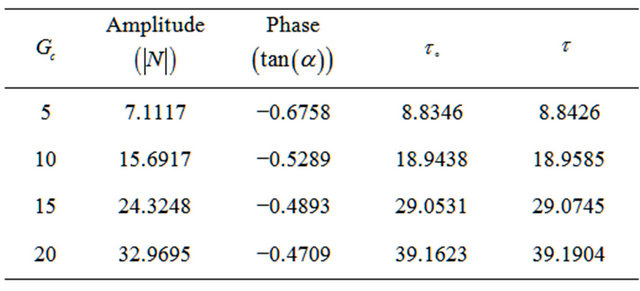
Table 4. Values of amplitude, phase and the skin friction coefficients for different values of Kp with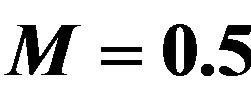 ,
, 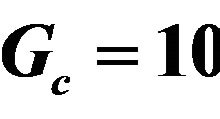 ,
, 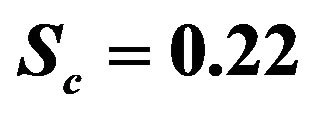 ,
, 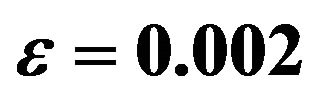 ,
, 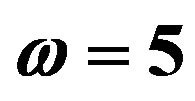 and
and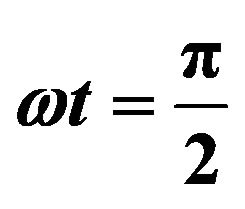 .
.

In Tables 1-5, the numerical values of skin friction coefficients 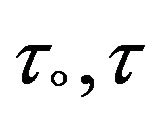 in terms of amplitude
in terms of amplitude 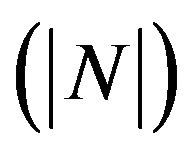 and phase
and phase  for different values of M, Sc, Gc, Kp and
for different values of M, Sc, Gc, Kp and  are entered, respectively. It is noted that the value of the phase
are entered, respectively. It is noted that the value of the phase 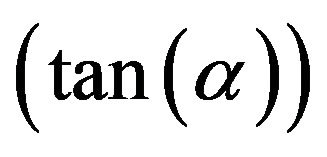 increases due to decrease in
increases due to decrease in  while increases due to increase in M, Sc, Gc and Kp. Also, It is observed that an increasing in Gc and Kp leads to an increasing in the value of amplitude
while increases due to increase in M, Sc, Gc and Kp. Also, It is observed that an increasing in Gc and Kp leads to an increasing in the value of amplitude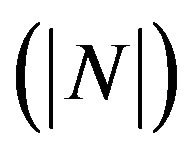 while an increase of M, Sc and
while an increase of M, Sc and  leads to a decrease in the value of
leads to a decrease in the value of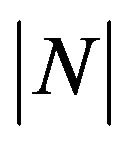 . Further, it is showed that the skin friction coefficients
. Further, it is showed that the skin friction coefficients 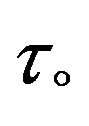 and
and 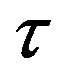 increase due to increase in Gc, Kp while decrease due to increase in M, Sc and
increase due to increase in Gc, Kp while decrease due to increase in M, Sc and  with note that
with note that 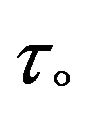 is not function on
is not function on .
.
In Tables 6 and 7, present the numerical values of amplitude , phase
, phase 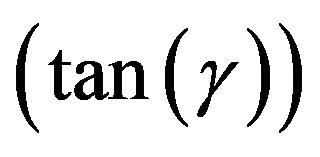 and the rate of mass transfer in term of Sherwood number Sh due to the variations in the values of Sc and
and the rate of mass transfer in term of Sherwood number Sh due to the variations in the values of Sc and , respectively. It is watched that an increase in Sc results in an increase in
, respectively. It is watched that an increase in Sc results in an increase in
Table 5. Values of amplitude, phase and the skin friction coefficients for different values of 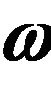 with
with ,
, 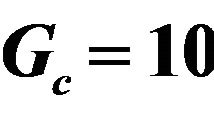 ,
,  ,
,  ,
, 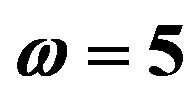 and
and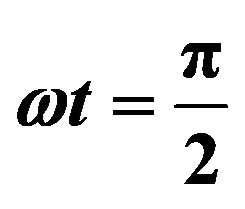 .
.

Table 6. Values of amplitude, phase and the rate of mass transfer for different values of Sc with 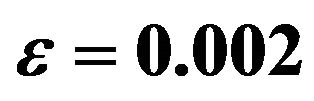 and
and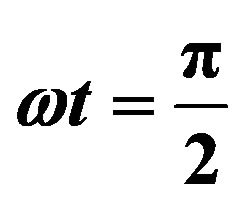 .
.
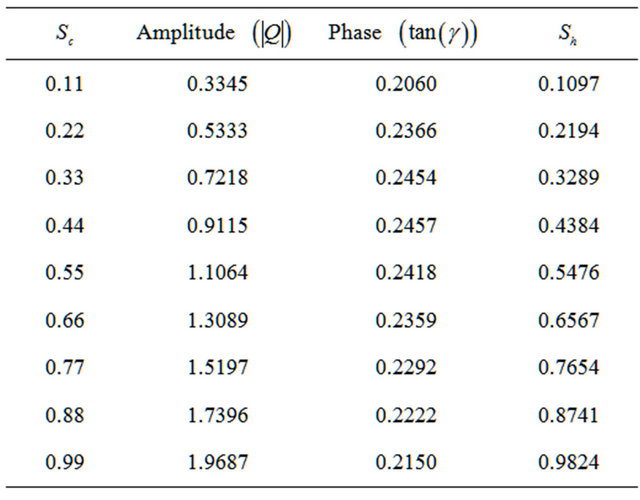
Table 7. Values of amplitude, phase and the rate of mass transfer for different values of  with
with 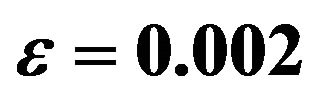 and
and .
.
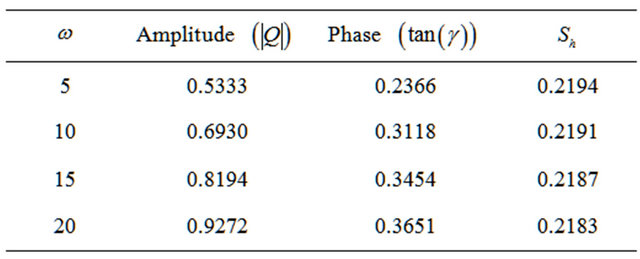
 and Sh but the phase
and Sh but the phase  increases at 0.11 ≤ Sc ≤ 0.44 while it decreases at
increases at 0.11 ≤ Sc ≤ 0.44 while it decreases at . An increase in
. An increase in results in an increase in
results in an increase in  and
and 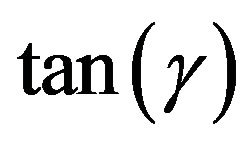 and a decrease in Sh.
and a decrease in Sh.
5. Conclusions
The above study shows up the following results of physical interest on the velocity and concentration distribution of the flow field.
• The magnetic field parameter M slows down the velocity of the flow field at all points due to the magnetic pull of the Lorentz force acting on the flow field.
• The Schmidt number Sc reveals that the presence of heavier diffusion species has a delaying effect on velocity of the flow field.
• The Grashof number for mass transfer Gc is accelerated the velocity of the flow field at all points.
• The effect of porosity parameter Kp is enhanced the velocity of the flow field at all points.
• The concentration distribution decreases at all points of the flow field with the increase of the Schmidt number Sc. It means that a greater delaying effect on the concentration distribution is due to the heavier diffusing species of the flow field.
• The value of the phase  increases due to decrease in
increases due to decrease in  while increases due to increase in M, Sc, Gc and Kp.
while increases due to increase in M, Sc, Gc and Kp.
• An increasing in Gc and Kp leads to an increasing in the value of amplitude 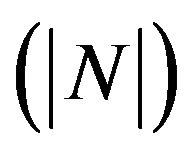 while an increase of M, Sc and
while an increase of M, Sc and  leads to a decrease in the value of
leads to a decrease in the value of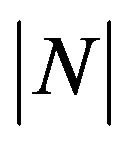 .
.
• The skin friction coefficients  and
and  increase due to increase in Gc, Kp while decrease due to increase in M, Sc and
increase due to increase in Gc, Kp while decrease due to increase in M, Sc and  with note that
with note that 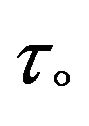 is not function on
is not function on .
.
• An increase in Sc results in an increase in  and Sh but the phase
and Sh but the phase 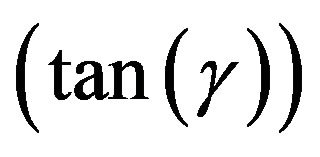 increases at 0.11 ≤ Sc ≤ 0.44 while it decreases at Sc ≥ 0.55.
increases at 0.11 ≤ Sc ≤ 0.44 while it decreases at Sc ≥ 0.55.
• An increase in  results in an increase in
results in an increase in  and
and 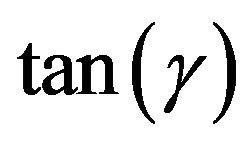 and a decrease in Sh.
and a decrease in Sh.
REFERENCES
- G. A. Georgantopoulos, J. Koullias, C. L. Goudas and C. Courogenis, “Free Convection and Mass Transfer Effects on the Hydro-Magnetic Oscillatory Flow past an Infinite Vertical Porous Plate,” Astrophysics and Space Science, Vol. 74, No. 2, 1981, pp. 357-389. doi:10.1007/BF00656444
- T. Hayat, S. Ashgar and A. M. Siddiqui, “Periodic Unsteady Flows of a Non-Newtonian Fluid,” Acta Mechanica, Vol. 131, No. 3-4, 1998, pp. 169-175.
- S. Ashgar, M. R. Mohyuddin, T. Hayat and A. M. Siddiqui, “The Flow of Non-Newtonian Fluid Induced Due to the Oscillations of a Porous Plate,” Mathematical Problems in Engineering, Vol. 2, 2003, pp. 133-143.
- P. Singh and C. B. Gupta, “MHD Free Convective Flow of a Viscous Fluid through a Porous Medium Bounded by an Oscillating Porous Plate in Slip Flow Regime with Mass Transfer,” Indian Journal of Theoretical Physics, Vol. 53, No. 2, 2005, pp. 111-120.
- S. S. Das, S. K. Sahoo and G. C. Dash, “Numerical Solution of Mass Transfer Effects on Unsteady Flow past an Accelerated Vertical Porous Plate with Suction,” Bulletin of the Malaysian Mathematical Sciences Society, Vol. 29, No. 1, 2006, pp. 33-42.
- A. Raptis, “Unsteady Free Convection Flow through Porous Medium,” International Journal of Engineering Science, Vol. 21, No. 4, 1983, pp. 345-349. doi:10.1016/0020-7225(83)90118-0
- M. A. Hossain and R. A. Begum, “Effect of Mass Transfer and Free Convection on the Flow past a Vertical Plate,” Journal of Heat Transfer, Vol. 106, 1984, pp. 664-668. doi:10.1115/1.3246735
- S. S. Das, M. Maity and J. K. Das, “Unsteady Hydromagnetic Convective Flow past an Infinite Vertical Porous Flat Plate in a Porous Medium,” International Journal of Energy and Environment, Vol. 1, No. 3, 2012, pp. 109-118.
- A. K. Singh, A. K. Singh and N. P. Singh, “Heat and Mass Transfer in MHD Flow of a Viscous Fluid past a Vertical Plate under Oscillatory Suction Velocity,” Indian Journal of Pure and Applied Mathematics, Vol. 34, No. 3, 2003, pp. 429-442.
Nomenclatures
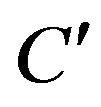 Species concentration;
Species concentration;
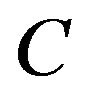 Non-dimension species concentration;
Non-dimension species concentration;
 Molecular diffusivity;
Molecular diffusivity;
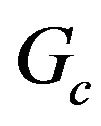 Grashof number for mass transfer;
Grashof number for mass transfer;
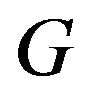 Acceleration due to gravity;
Acceleration due to gravity;
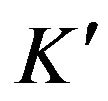 Permeability of the medium;
Permeability of the medium;
 Permeability/porosity parameter;
Permeability/porosity parameter;
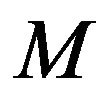 Magnetic parameter;
Magnetic parameter;
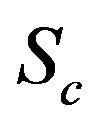 Schmidt number;
Schmidt number;
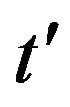 Time;
Time;
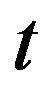 Non-dimension time;
Non-dimension time;
 Velocity component along x-axis;
Velocity component along x-axis;
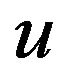 Non-dimension velocity component along x-axis;
Non-dimension velocity component along x-axis;
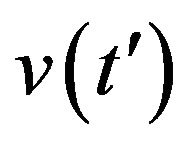 Suction velocity;
Suction velocity;
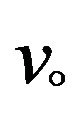 Positive constant suction velocity;
Positive constant suction velocity;
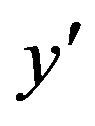 Distance along y-axis;
Distance along y-axis;
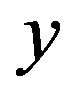 Non-dimension distance along y-axis;
Non-dimension distance along y-axis;
 Volumetric coefficient of expansion with species concentration;
Volumetric coefficient of expansion with species concentration;
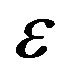 A small positive constant
A small positive constant 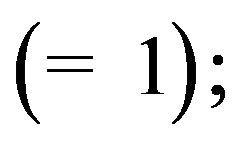
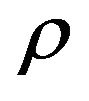 Density of fluid;
Density of fluid;
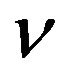 Kinematic coefficient of viscosity;
Kinematic coefficient of viscosity;
 Frequency of oscillation;
Frequency of oscillation;
 Non-dimension frequency of oscillation;
Non-dimension frequency of oscillation;
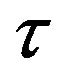 Skin friction;
Skin friction;
 Electrical conductivity;
Electrical conductivity;
 Subscript condition far away from the plate;
Subscript condition far away from the plate;
 Superscript means
Superscript means  (used in Equations (7)- (10));
(used in Equations (7)- (10));
 Sherwood number.
Sherwood number.
Appendix