Applied Mathematics
Vol. 3 No. 11 (2012) , Article ID: 24516 , 6 pages DOI:10.4236/am.2012.311232
Integral Inequalities of Hermite-Hadamard Type for Functions Whose 3rd Derivatives Are s-Convex
1College of Mathematics, Inner Mongolia University for Nationalities, Tongliao, China
2Department of Mathematics, School of Science, Tianjin Polytechnic University, Tianjin, China
Email: chunling1980@qq.com, qifeng618@gmail.com
Received September 2, 2012; revised October 2, 2012; accepted October 10, 2012
Keywords: Integral Inequality; Hermite-Hadamard’s Integral Inequality; s-Convex Function; Derivative; Mean
ABSTRACT
In the paper, the authors find some new inequalities of Hermite-Hadamard type for functions whose third derivatives are s-convex and apply these inequalities to discover inequalities for special means.
1. Introduction
The following definition is well known in the literature.
Definition 1.1. A function 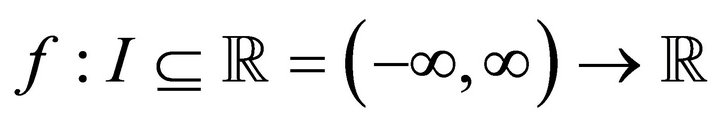 is said to be convex if
is said to be convex if

holds for all 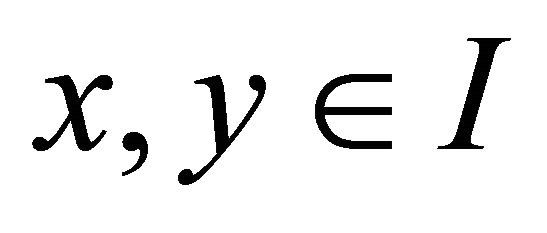 and
and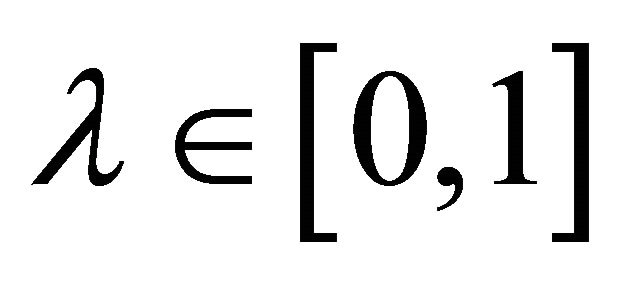 .
.
In [1,2], among others, the concepts of so-called quasiconvex and s-convex functions in the second sense was introduced as follows.
Definition 1.2 ([1]). A function 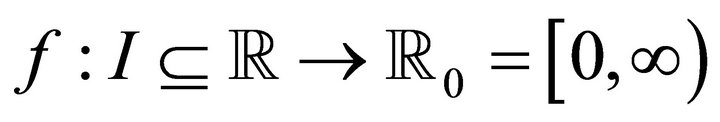 is said to be quasi-convex if
is said to be quasi-convex if
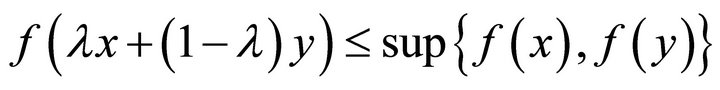
holds for all 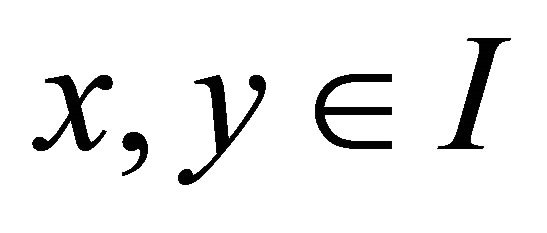 and
and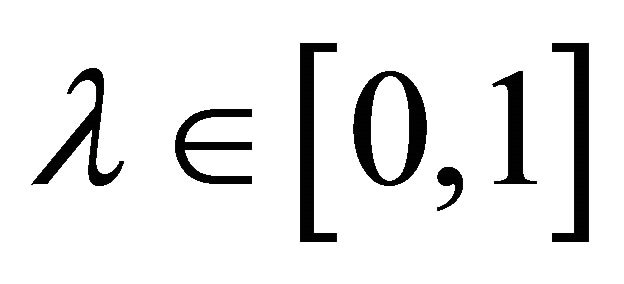 .
.
Definition 1.3 ([2]). Let A function
A function 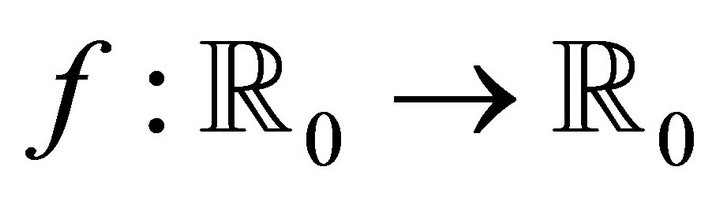 is said to be s-convex in the second sense if
is said to be s-convex in the second sense if
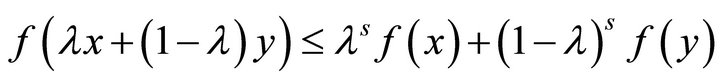
for all 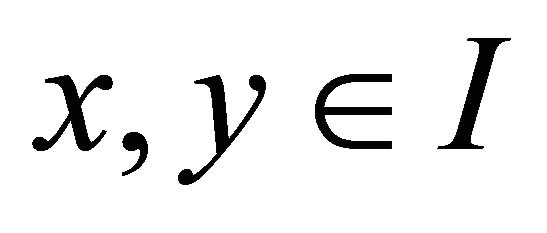 and
and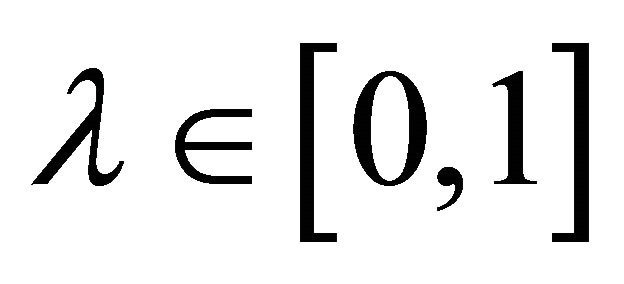 .
.
If  is a convex function on
is a convex function on 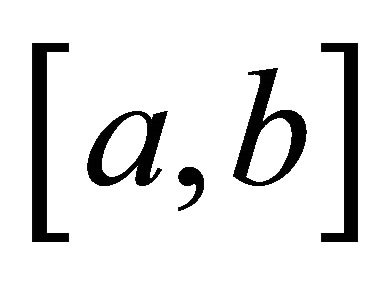 with
with 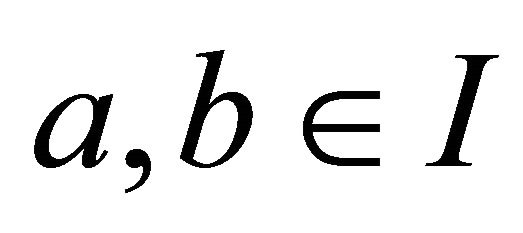 and
and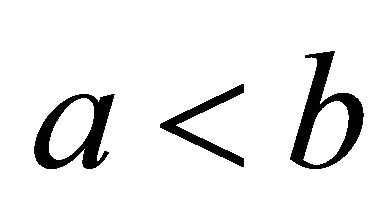 , Then we have Hermite-Hardamard’s inequality
, Then we have Hermite-Hardamard’s inequality
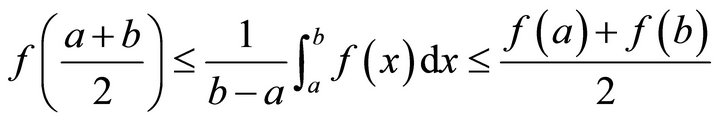 . (1.1)
. (1.1)
Hermite-Hadamard inequality (1.1) has been refined or generalized for convex, s-convex, and quasi-convex functions by a number of mathematicians. Some of them can be reformulated as follows.
Theorem 1.1 ([3, Theorems 2.2 and 2.3]). Let 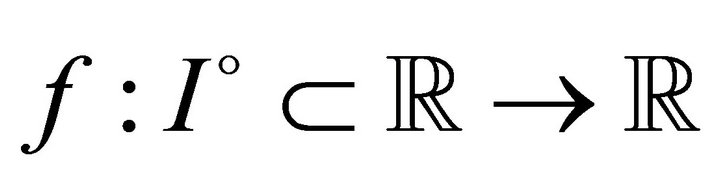 be a differentiable mapping on
be a differentiable mapping on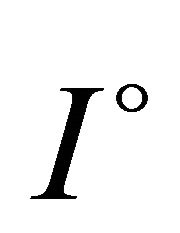 ,
,  with
with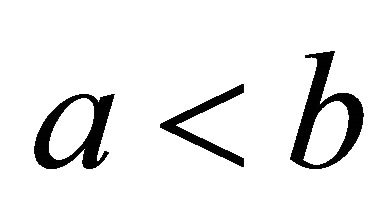 .
.
(1) If  is convex on
is convex on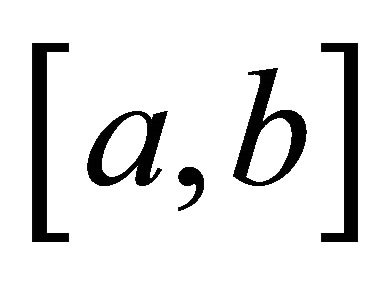 , then
, then
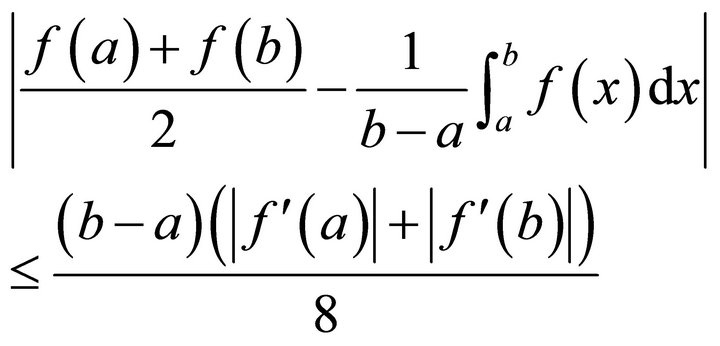 . (1.2)
. (1.2)
(2) If the new mapping 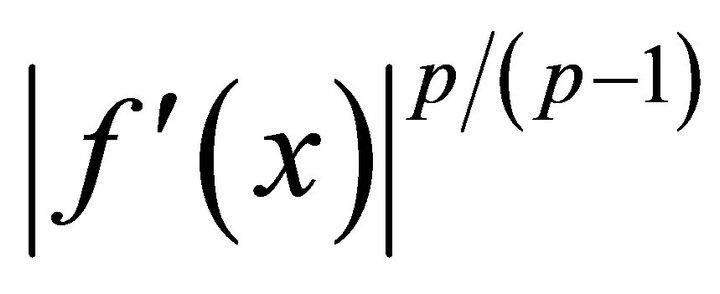 is convex on
is convex on
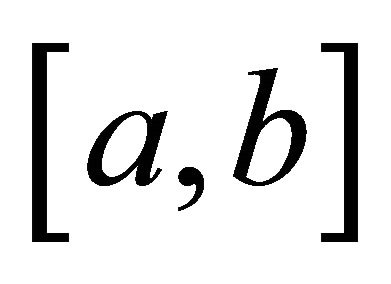 for
for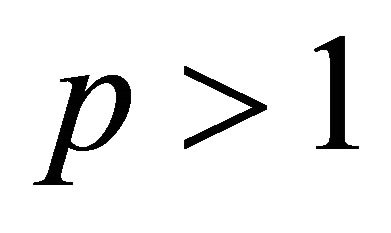 , then
, then

Theorem 1.2 ([4, Theorems 1 and 2]). Let 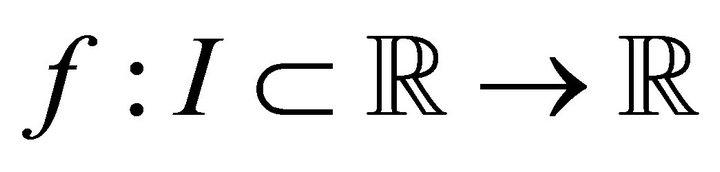 be a differentiable function on
be a differentiable function on 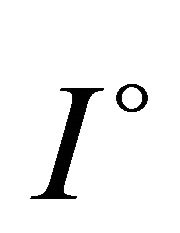 and
and  with
with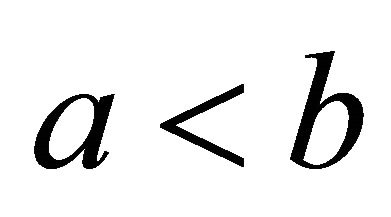 , and let
, and let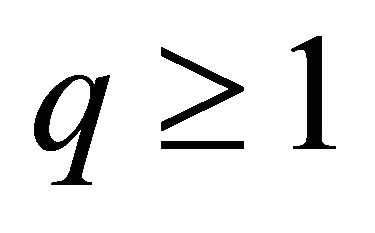 . If
. If 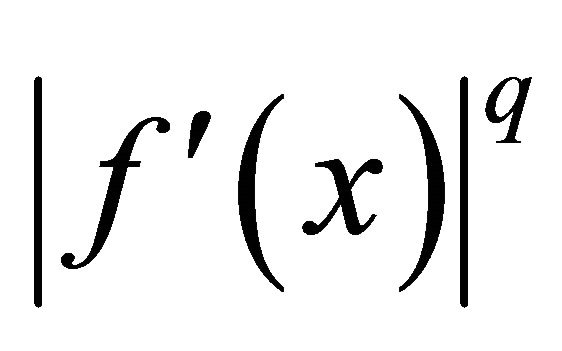 is convex on
is convex on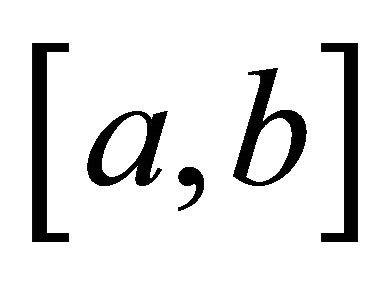 , then
, then
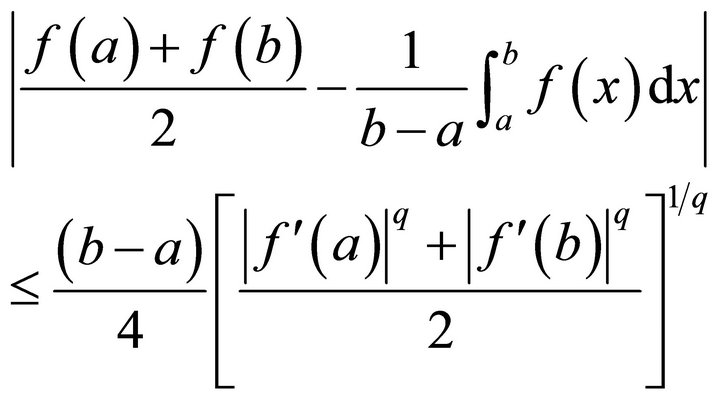 (1.3)
(1.3)
and
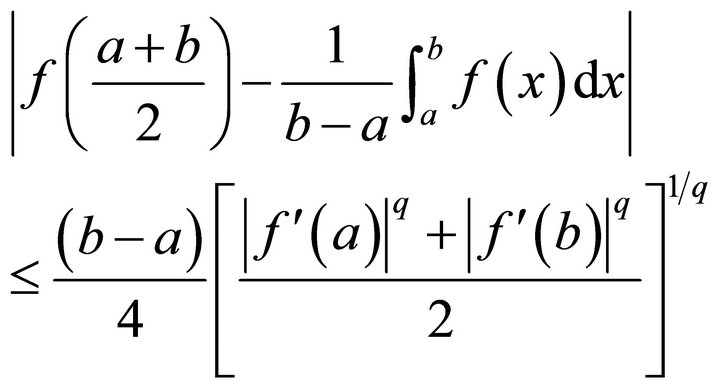 (1.4)
(1.4)
Theorem 1.3 ([5, Theorems 2.3 and 2.4]). Let 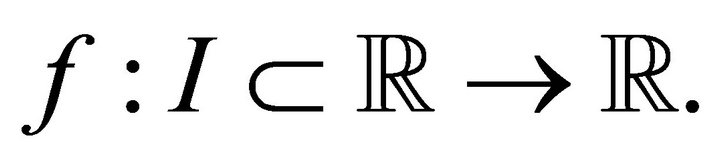 be differentiable on
be differentiable on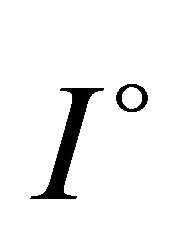 ,
, 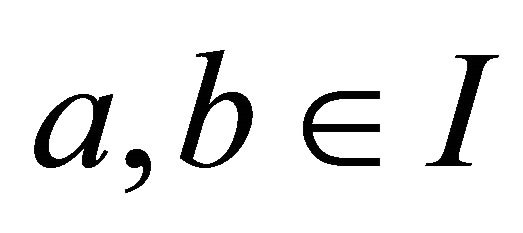 with
with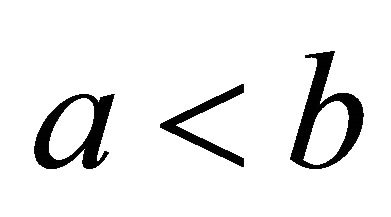 , and let
, and let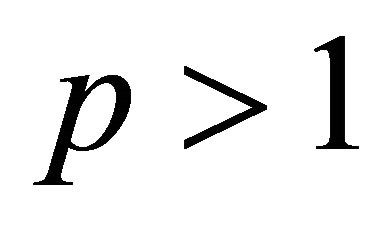 . If
. If 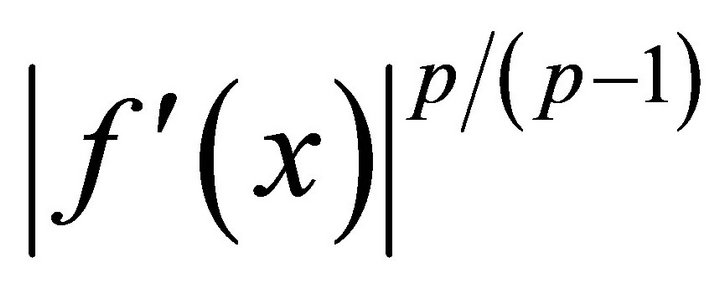 is convex on
is convex on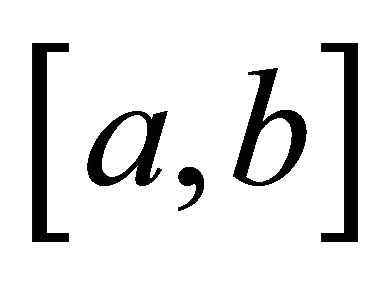 , then
, then
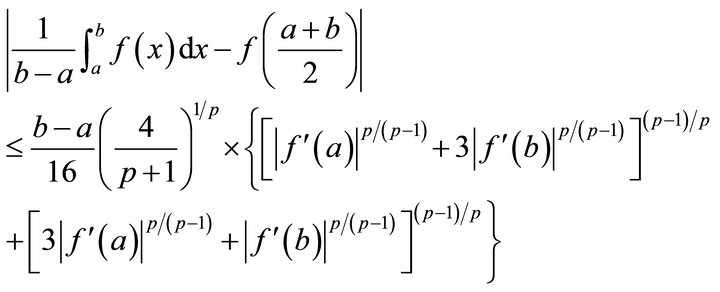
and
 (1.5)
(1.5)
Theorem 1.4 ([6, Theorems 1 and 3]). Let 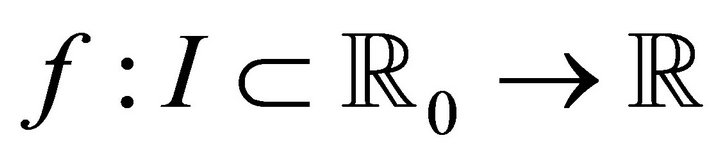 be differentiable on
be differentiable on 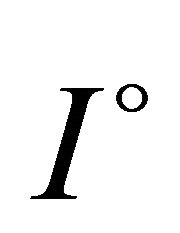 and
and 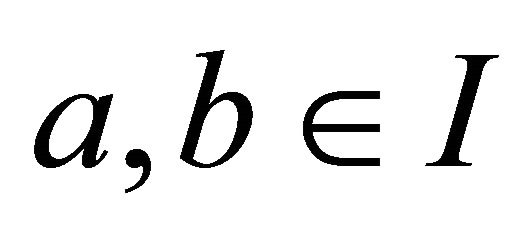 with
with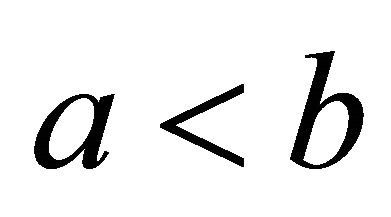 .
.
(1) If 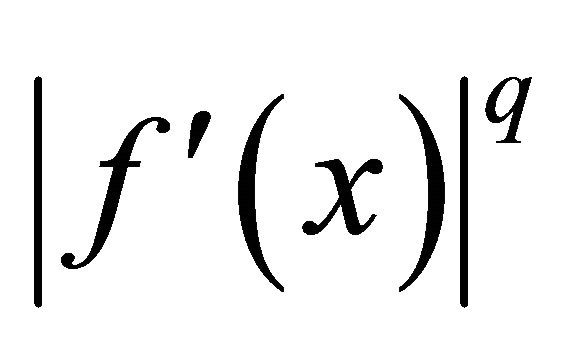 is s-convex on
is s-convex on 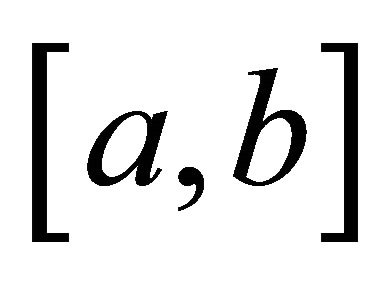 for some fixed
for some fixed 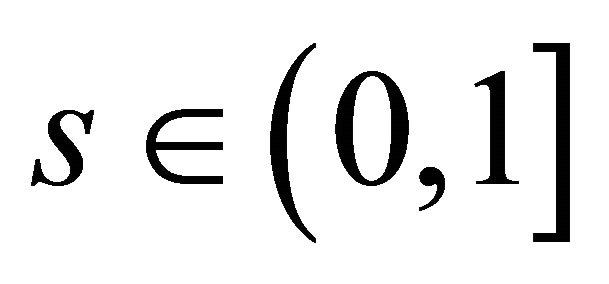 and
and , then
, then
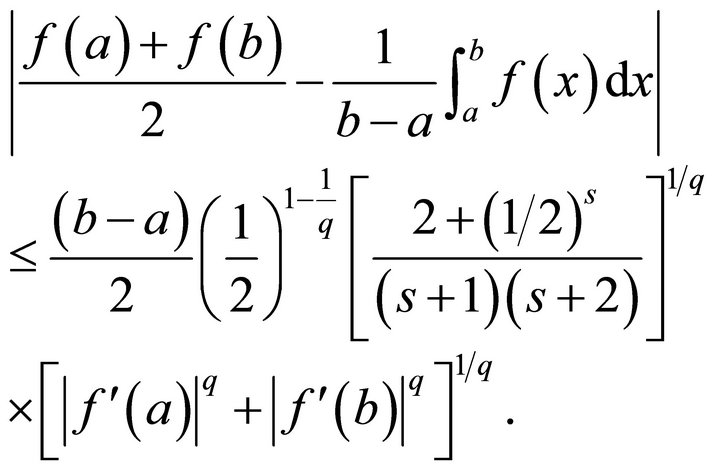 (1.6)
(1.6)
(2) If 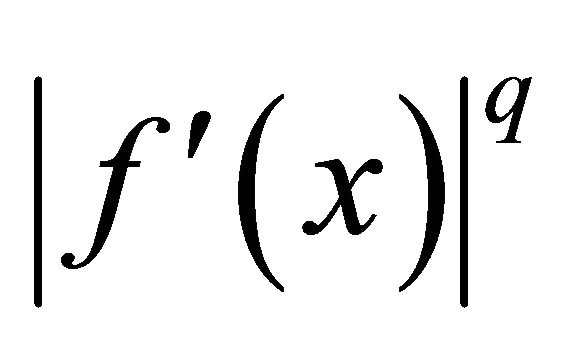 is s-convex on
is s-convex on 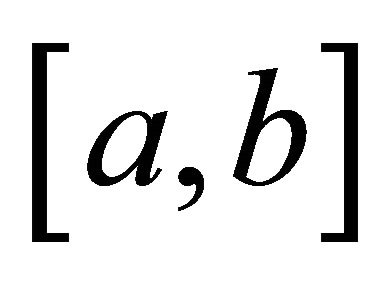 for some fixed
for some fixed 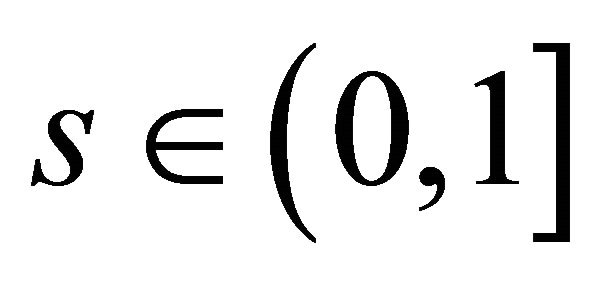 and
and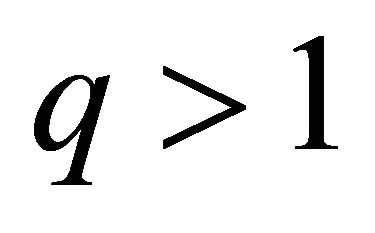 , then
, then
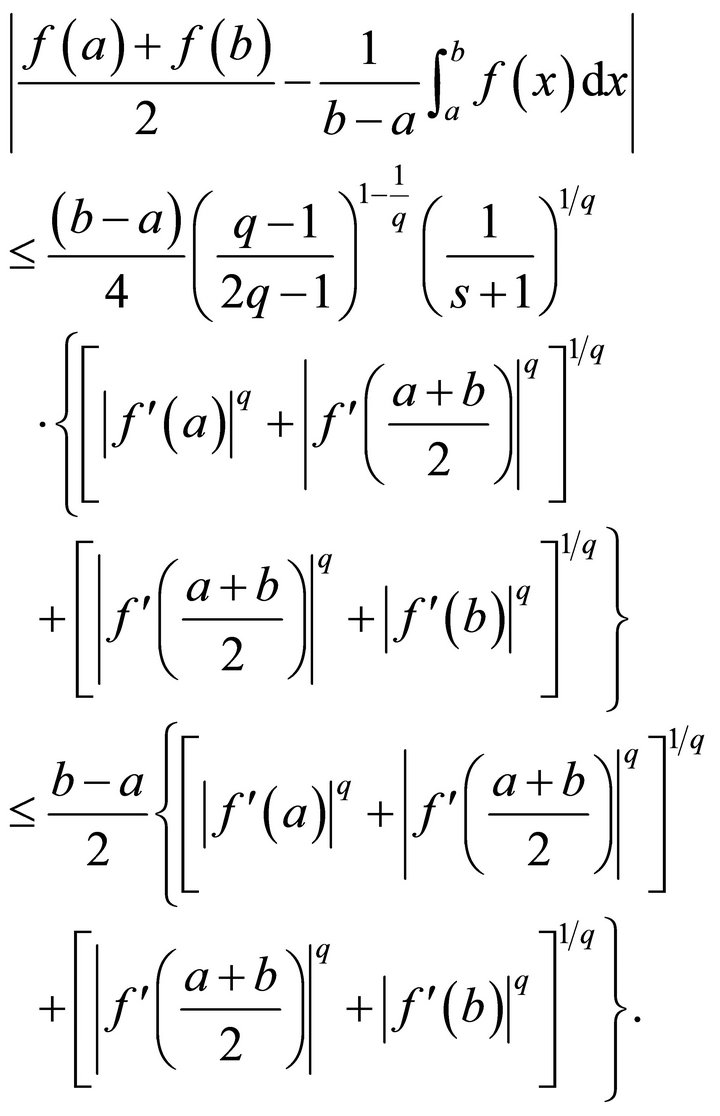 (1.7)
(1.7)
Theorem 1.5 ([7, Theorem 2]). Let 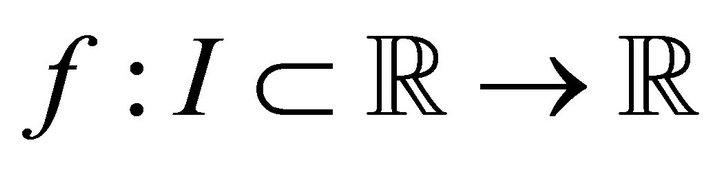 be an absolutely continuous function on
be an absolutely continuous function on 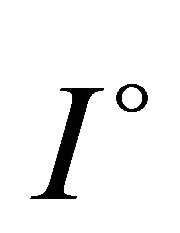 such that
such that 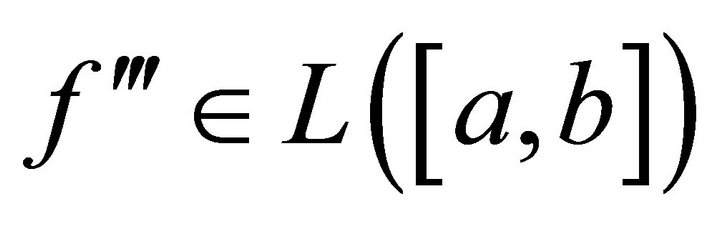 for
for 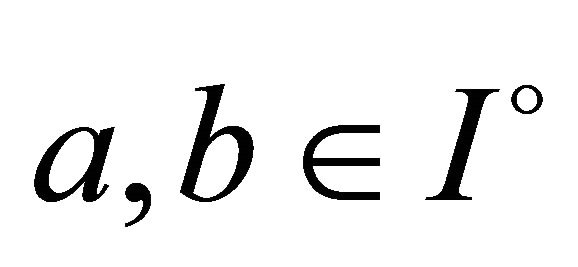 with
with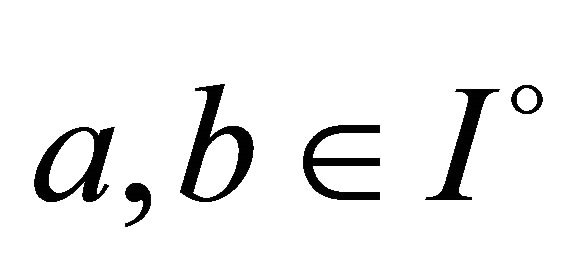 . If
. If  is quasi-convex on
is quasi-convex on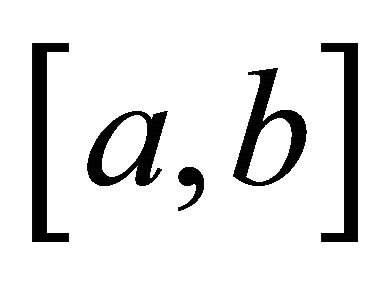 , then
, then
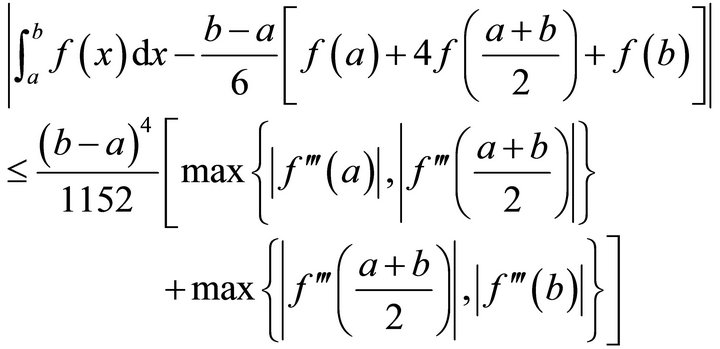
In recent years, some other kinds of Hermite-Hadamard type inequalities were created in, for example, [8-17], especially the monographs [18,19], and related references therein.
In this paper, we will find some new inequalities of Hermite-Hadamard type for functions whose third derivatives are s-convex and apply these inequalities to discover inequalities for special means.
2. A Lemma
For finding some new inequalities of Hermite-Hadamard type for functions whose third derivatives are 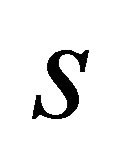 -convex, we need a simple lemma below.
-convex, we need a simple lemma below.
Lemma 2.1. Let 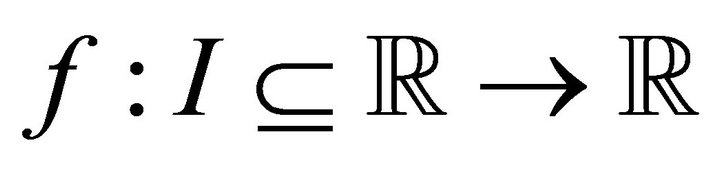 be a three times differentiable function on
be a three times differentiable function on 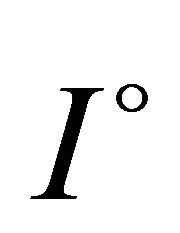 with
with 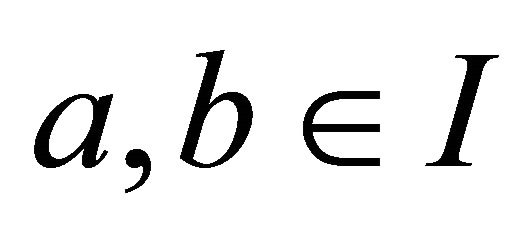 and
and . If
. If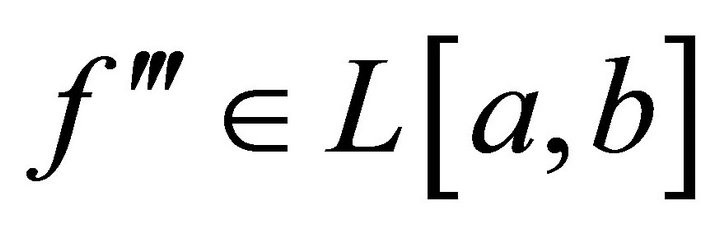 , then
, then
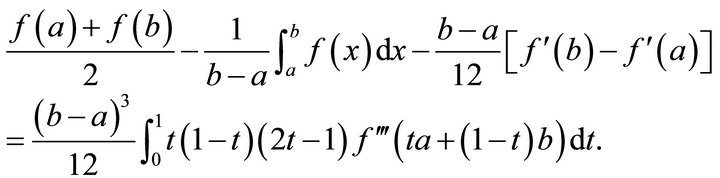 (2.1)
(2.1)
Proof. By integrating by part, we have
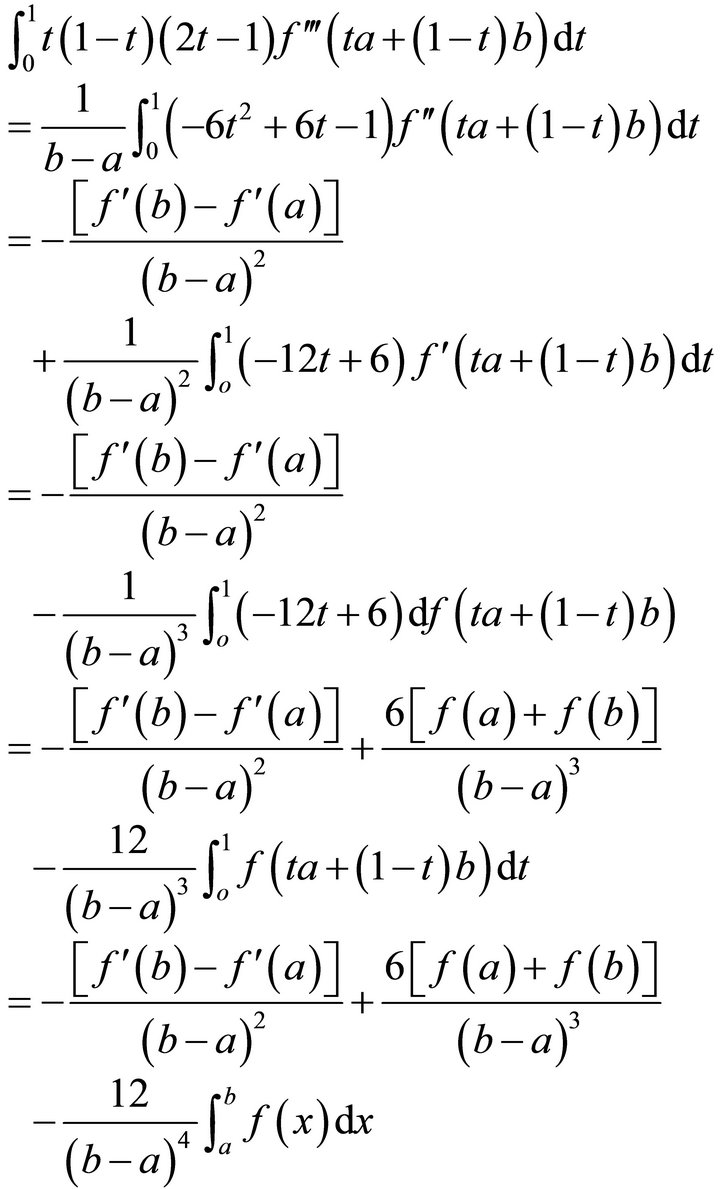
The proof of Lemma 2.1 is complete.
3. Some New Hermite-Hadamard Type Inequalities
We now utilize Lemma 2.1, Hölder’s inequality, and others to find some new inequalities of Hermite-Hadamard type for functions whose third derivatives are s-convex.
Theorem 3.1. Let 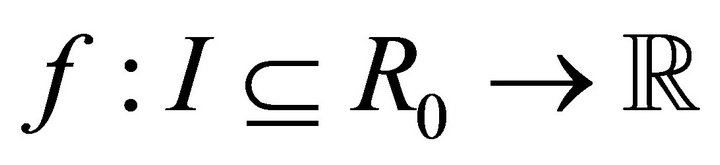 be a three times differentiable function on
be a three times differentiable function on 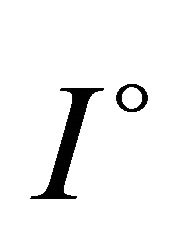 such that
such that 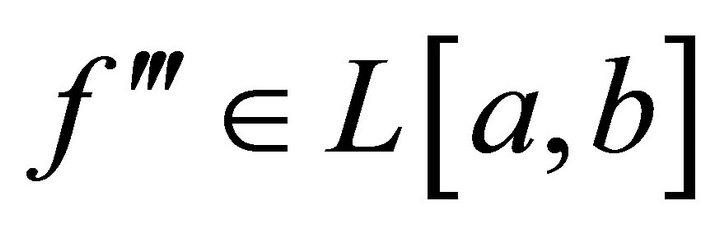 for
for 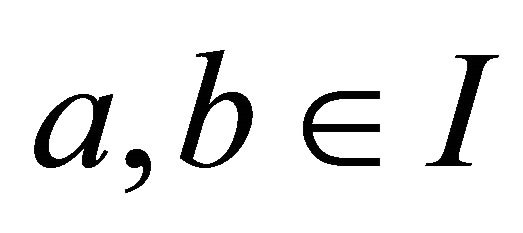 with
with . If
. If 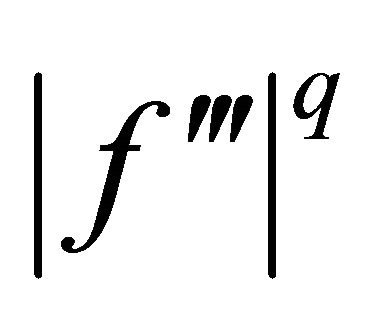 is s-convex on
is s-convex on  for some fixed
for some fixed 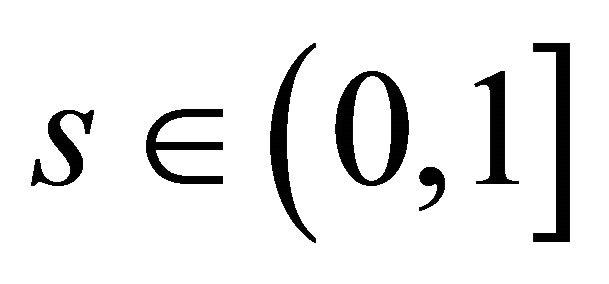 and
and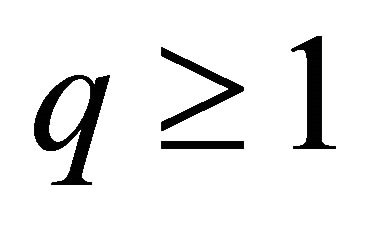 , then
, then
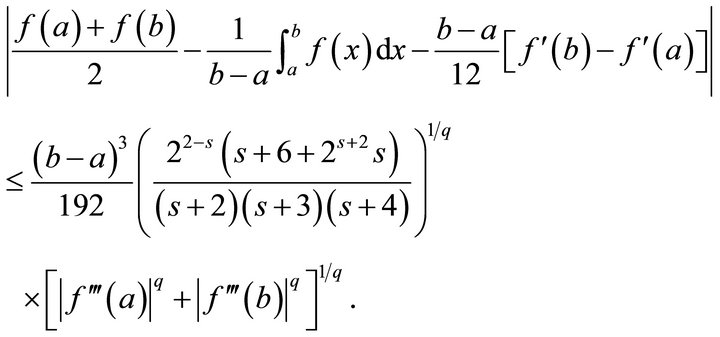 (3.1)
(3.1)
Proof. Since 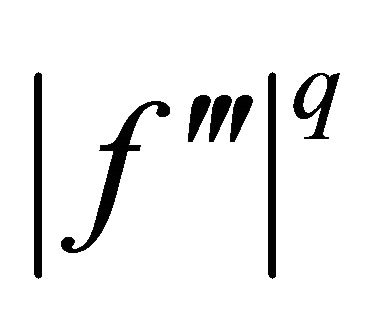 is s-convex on
is s-convex on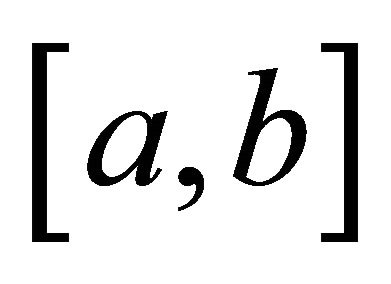 , by Lemma 2.1 and Hölder’s inequality, we have
, by Lemma 2.1 and Hölder’s inequality, we have
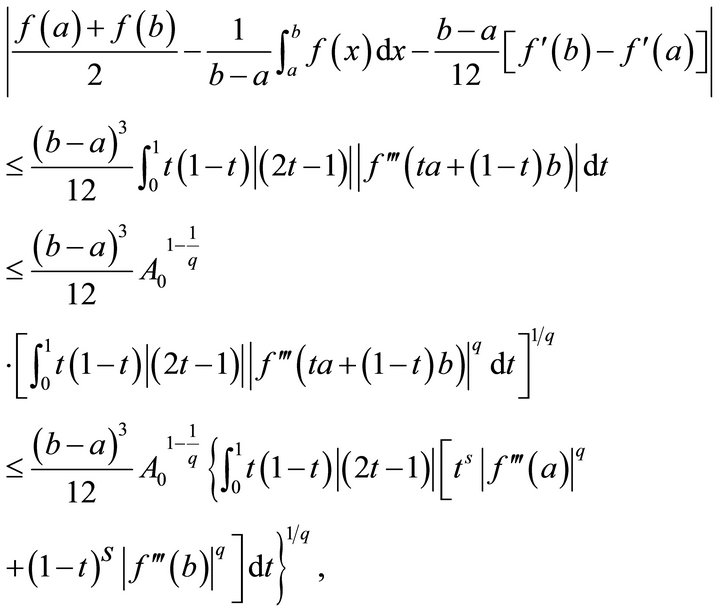
where
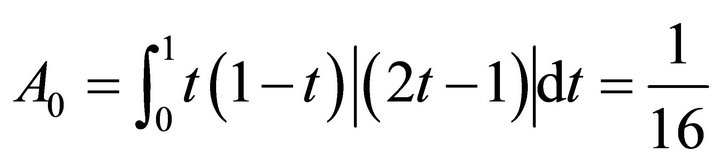
and
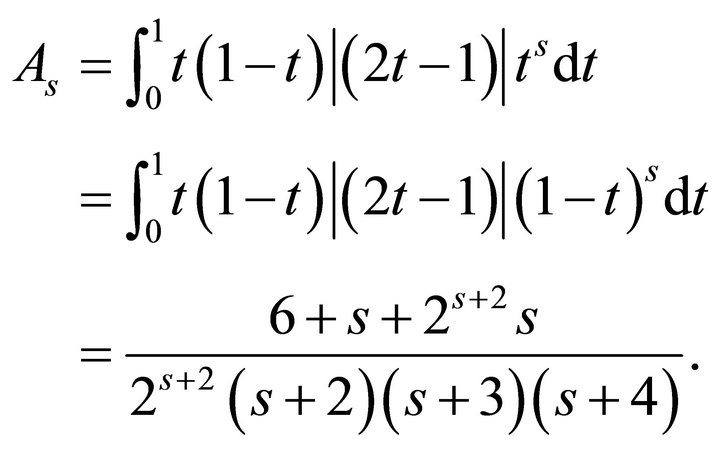
Thus, we have
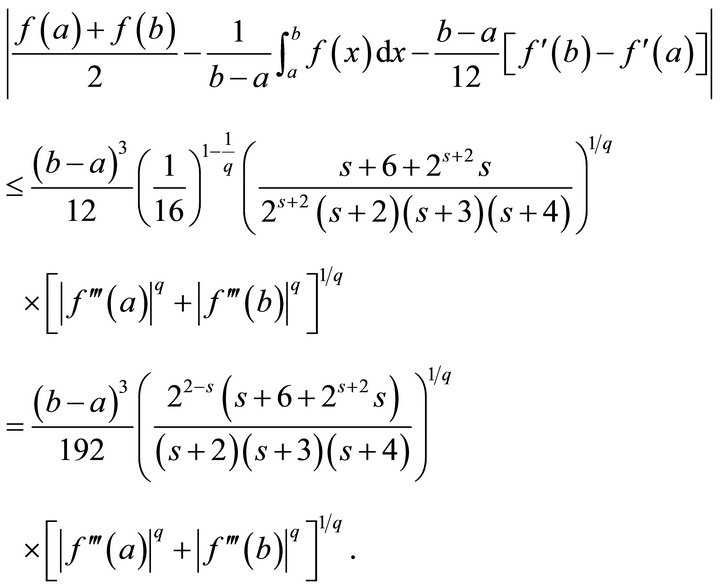
The proof of Theorem 3.1 is complete.
Corollary 3.1.1. Under conditions of Theorem 3.11) if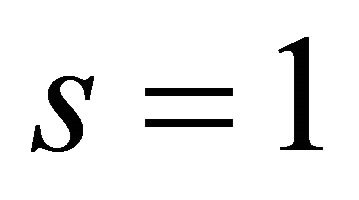 , then
, then
 (3.2)
(3.2)
2) if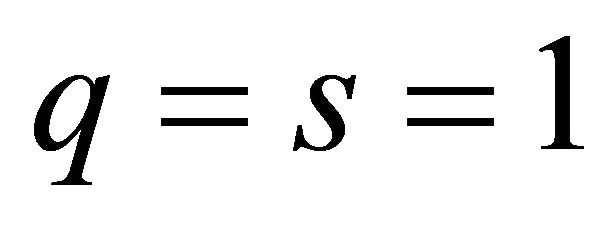 , then
, then
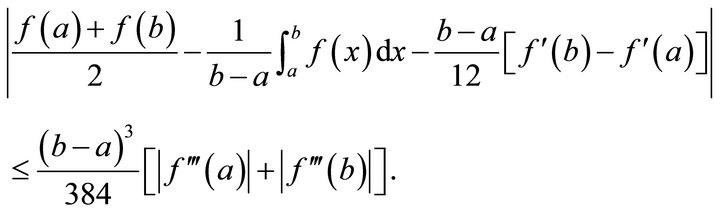
Theorem 3.2. Let  be a three times differentiable function on
be a three times differentiable function on  such that
such that 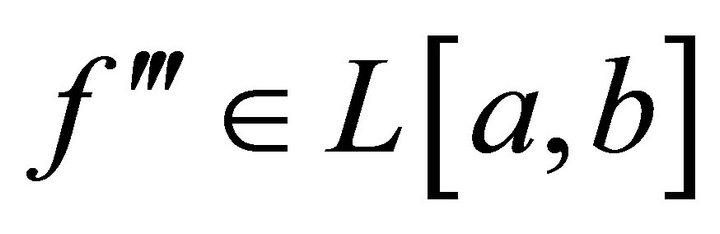 for
for 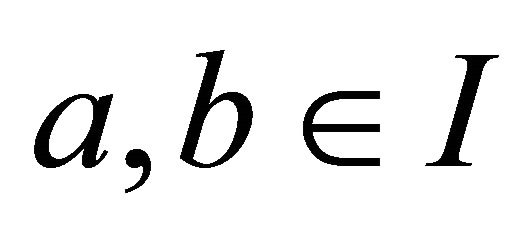 with
with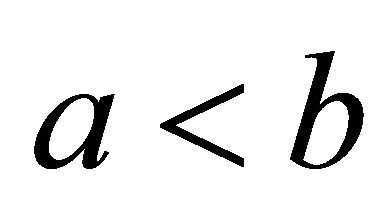 . If
. If 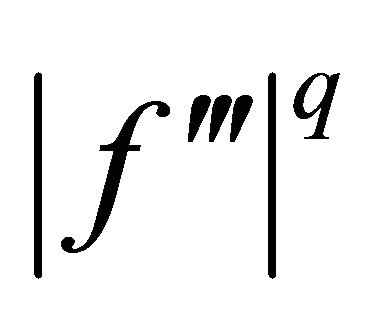 is s-convex on
is s-convex on 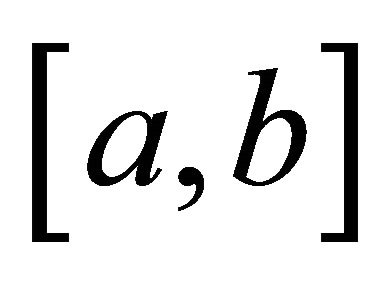 for some fixed
for some fixed 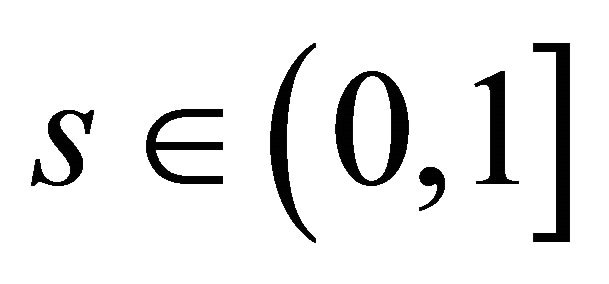 and
and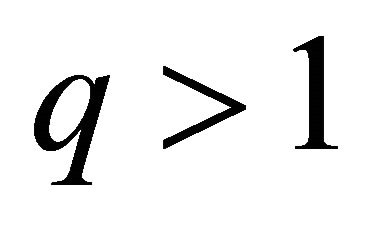 , then
, then
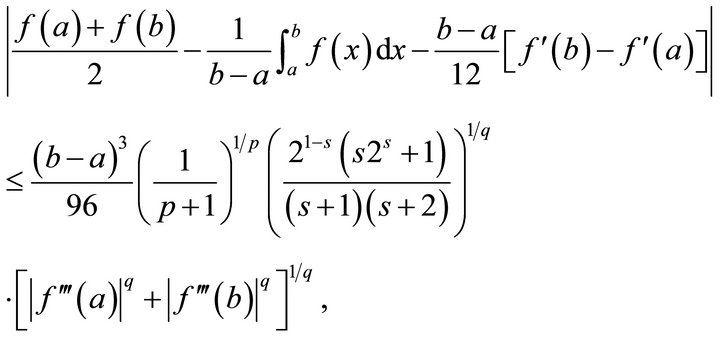 (3.3)
(3.3)
where 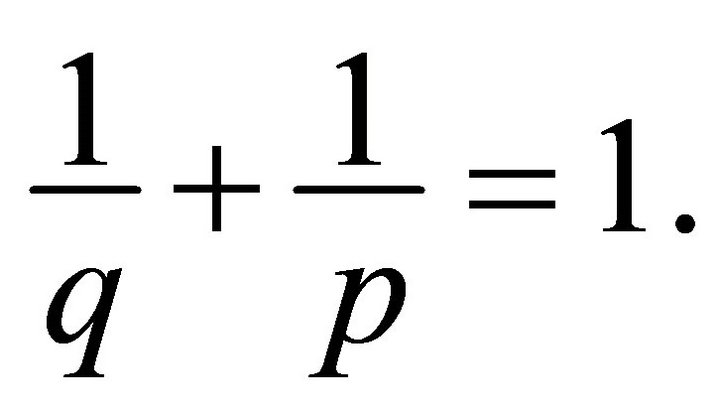
Proof. Using Lemma 2.1, the s-convexity of 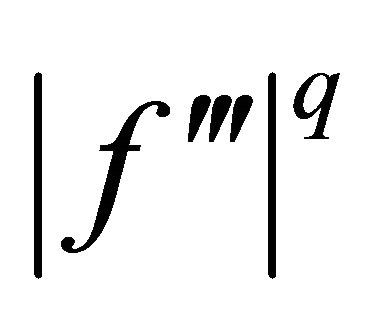 on
on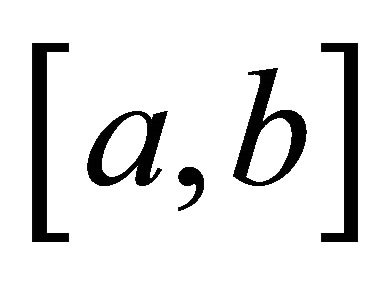 , and Hölder’s integral inequality yields
, and Hölder’s integral inequality yields
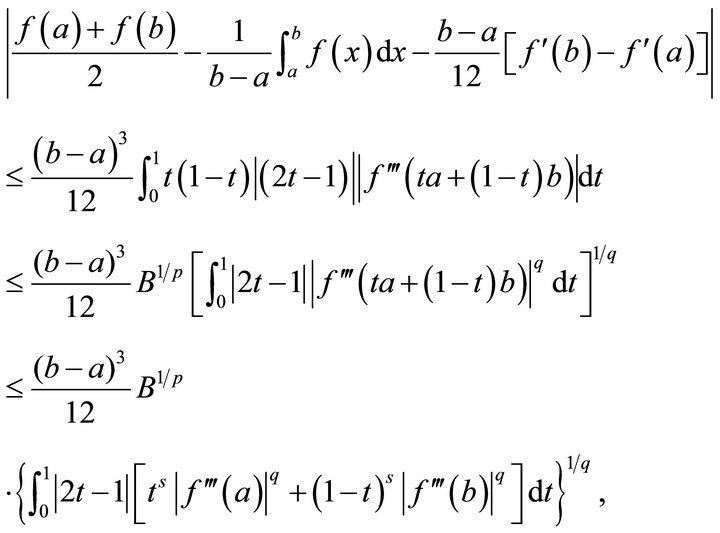
where an easy calculation gives
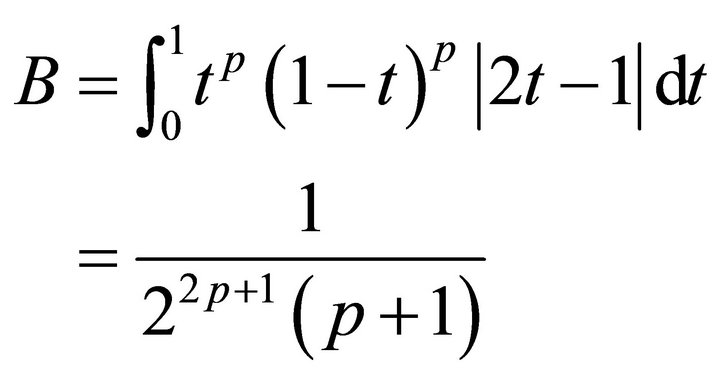 (3.4)
(3.4)
and
 (3.5)
(3.5)
Substituting Equations (3.4) and (3.5) into the above inequality results in the inequality (3.3). The proof of Theorem 3.2 is complete.
Corollary 3.2.1. Under conditions of Theorem 3.2, if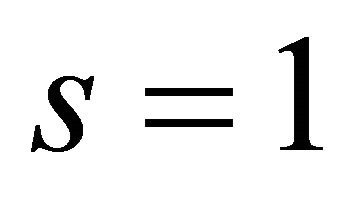 , then
, then

Theorem 3.3. Under conditions of Theorem 3.2, we have
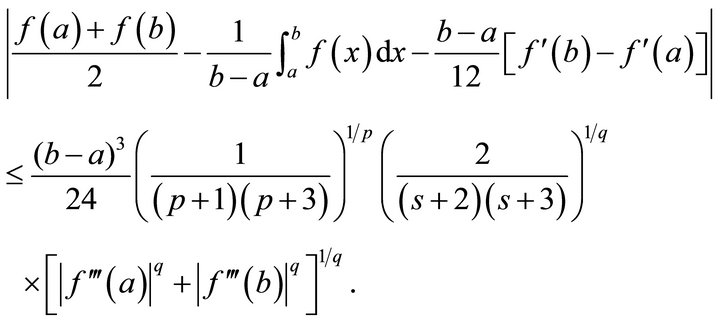 (3.6)
(3.6)
Proof. Making use of Lemma 2.1, the s-convexity of 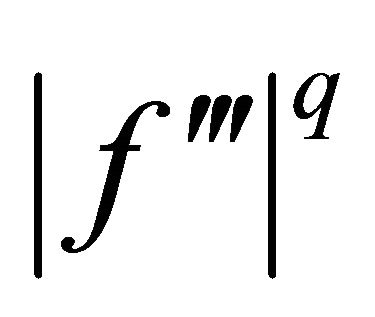 on
on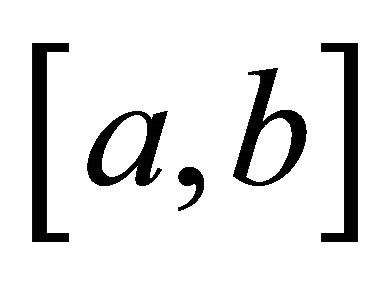 , and Hölder’s integral inequality leads to
, and Hölder’s integral inequality leads to
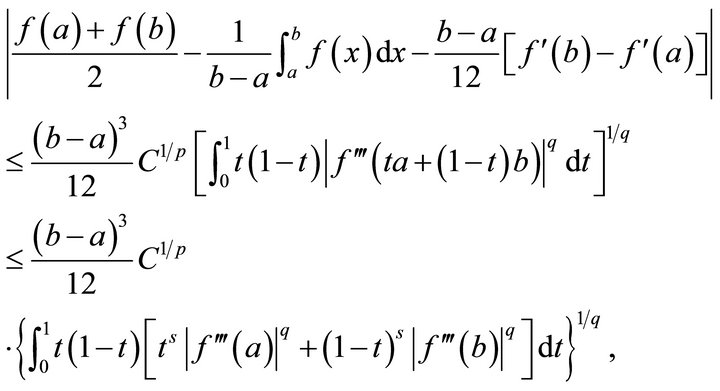
where
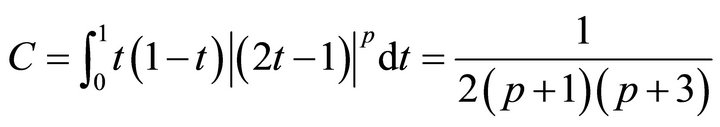 (3.7)
(3.7)
and
 (3.8)
(3.8)
Substituting Equations (3.7) and (3.8) into the above inequality derives the inequality (3.6). The proof of Theorem 3.3 is complete.
Corollary 3.3.1. Under conditions of Theorem 3.3, if s = 1, then
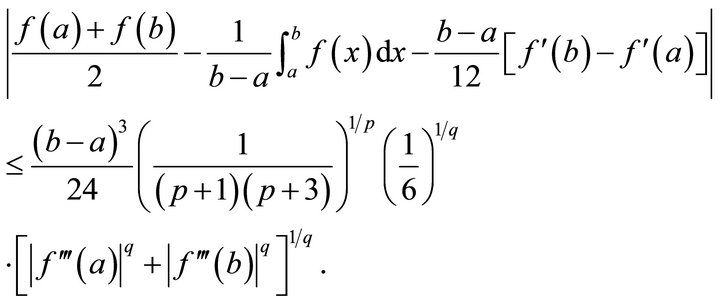
Theorem 3.4. Under conditions of Theorem 3.2, we have
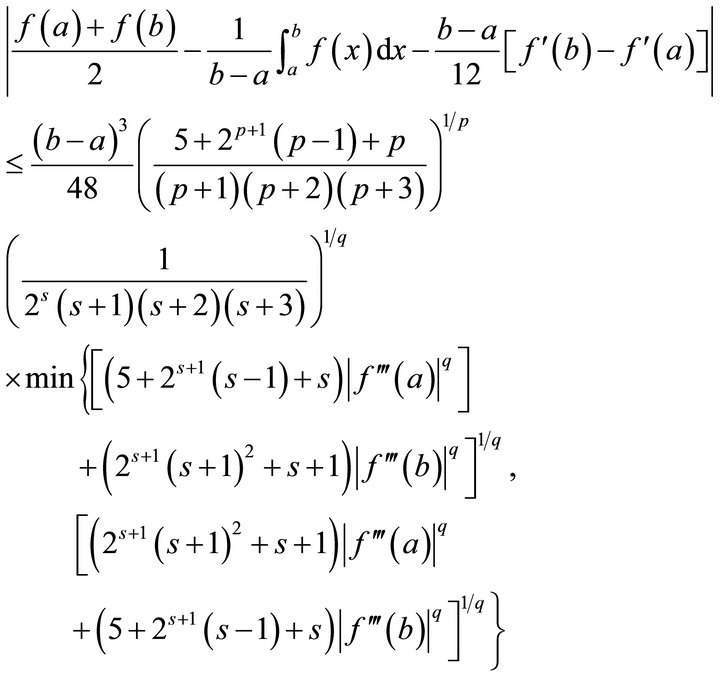
Proof. Since 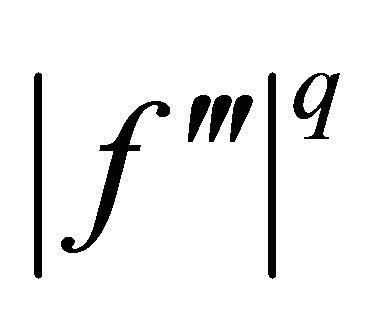 is s-convex on
is s-convex on , by Lemma 2.1 and Hölder’s inequality, we have
, by Lemma 2.1 and Hölder’s inequality, we have
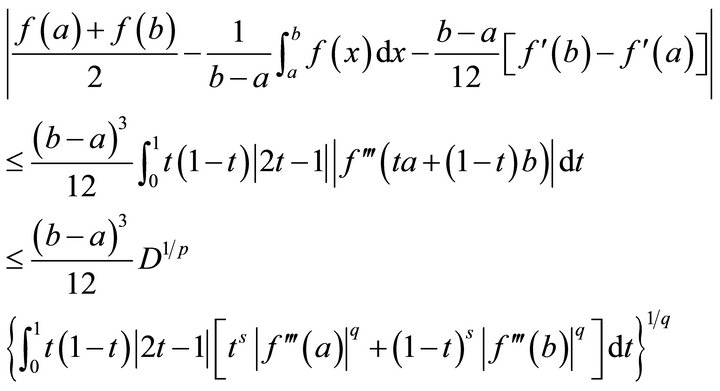
and
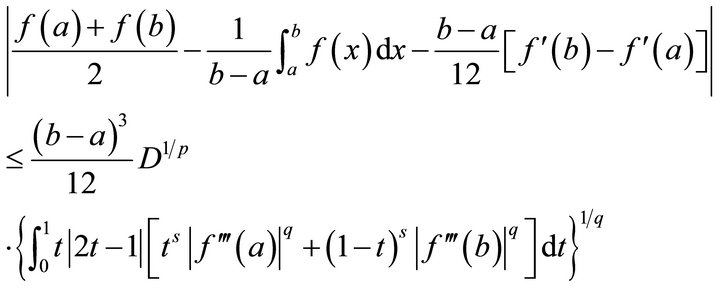
where a straightforward computation gives
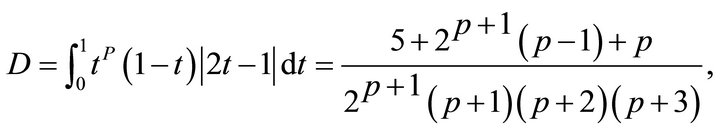
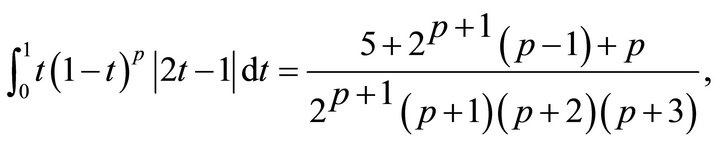
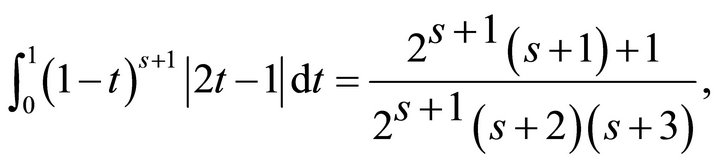
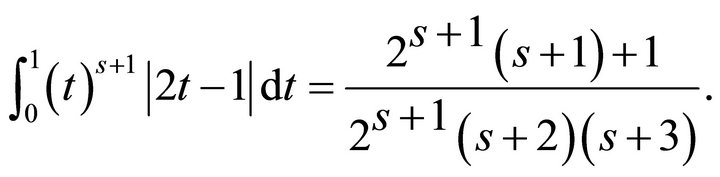
Substituting these equalities into the above inequality brings out the inequality (3.10). The proof of Theorem 3.4 is complete.
Corollary 3.4.1. Under conditions of Theorem 3.4, if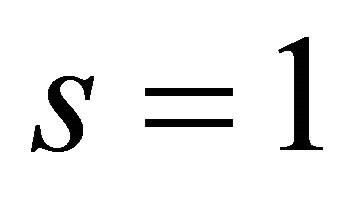 , then
, then
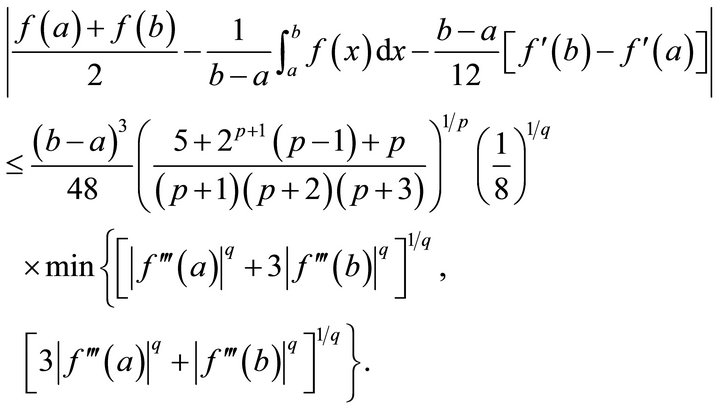
4. Applications to Special Means
For positive numbers 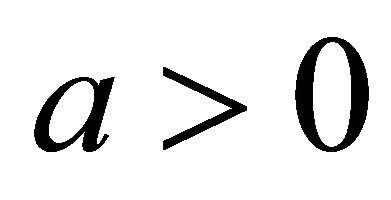 and
and , define
, define
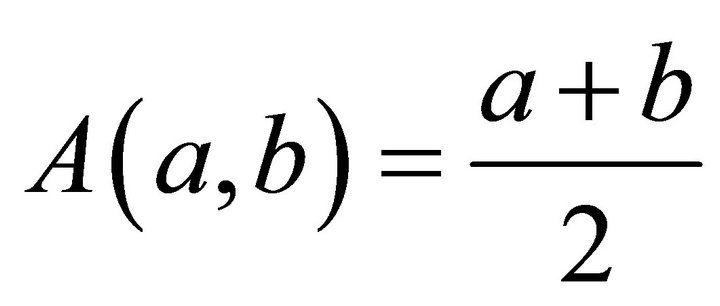 (4.1)
(4.1)
and
 (4.2)
(4.2)
It is well known that A and 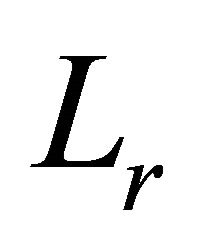 are respectively called the arithmetic and generalized logarithmic means of two positive number
are respectively called the arithmetic and generalized logarithmic means of two positive number  and
and .
.
Now we are in a position to construct some inequalities for special means A and 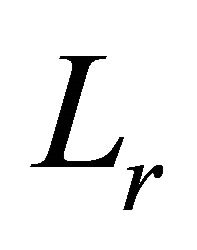 by applying the above established inequalities of Hermite-Hadamard type.
by applying the above established inequalities of Hermite-Hadamard type.
Let
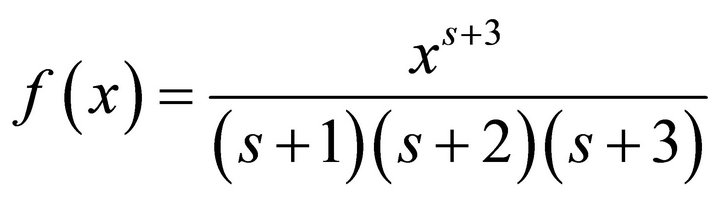 (4.3)
(4.3)
for 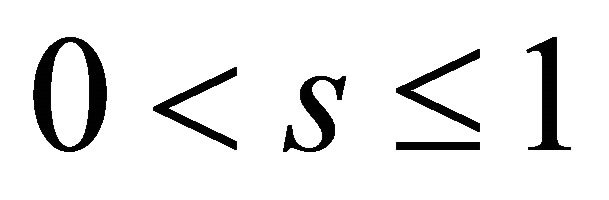 and
and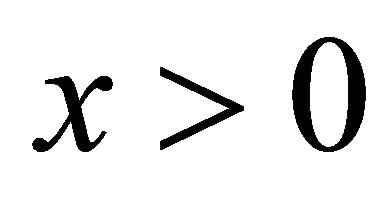 . Since
. Since 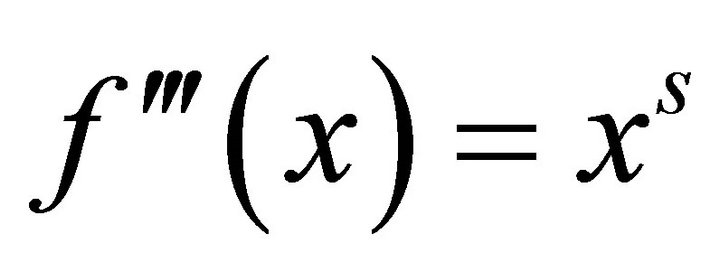 and
and
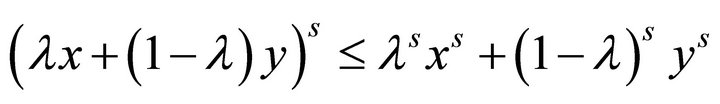
for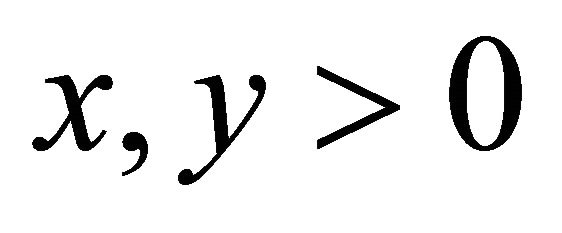 and
and 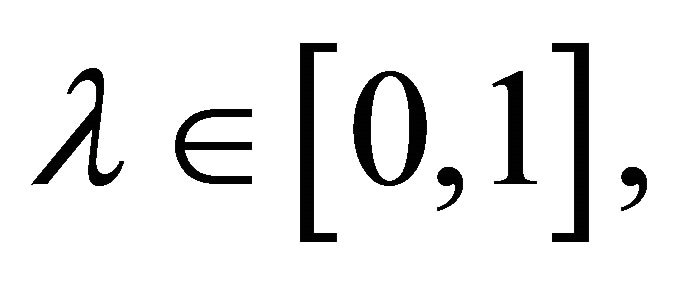 then
then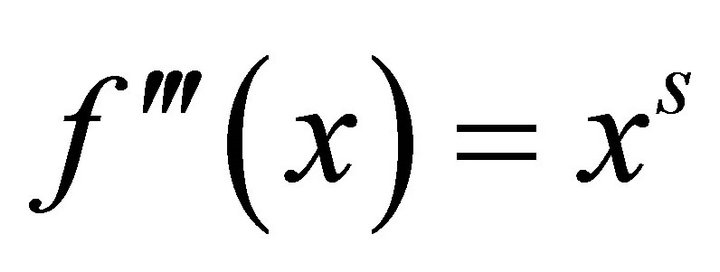 is s-convex function on
is s-convex function on 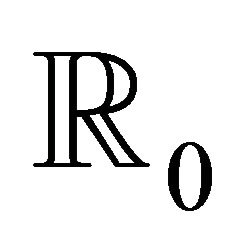 and
and
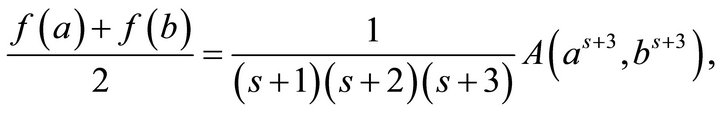
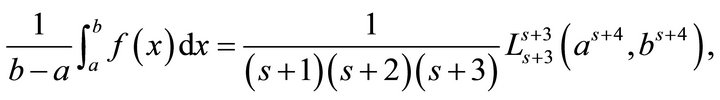
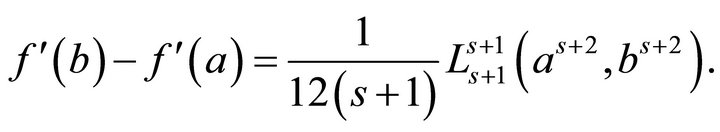
Applying the function (4.3) to Theorems 3.1 to 3.3 immediately leads to the following inequalities involving special means  and
and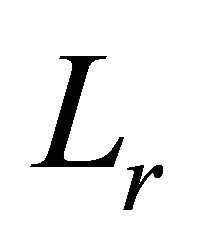 .
.
Theorem 4.1. Let 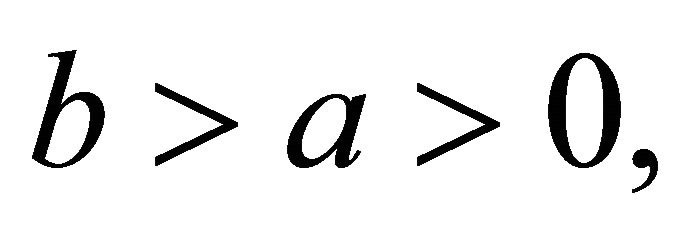
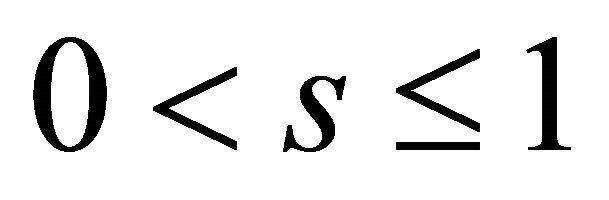 , and
, and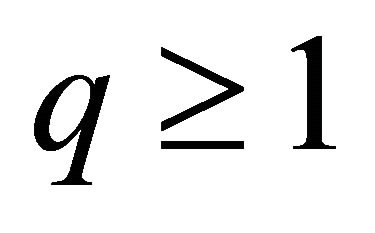 . Then
. Then
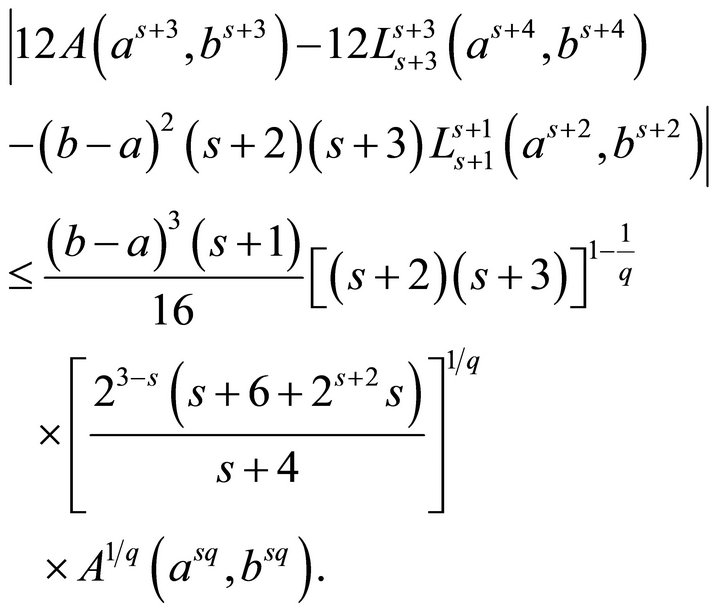
Theorem 4.2. For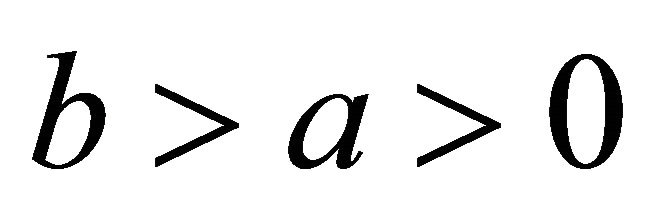 ,
, 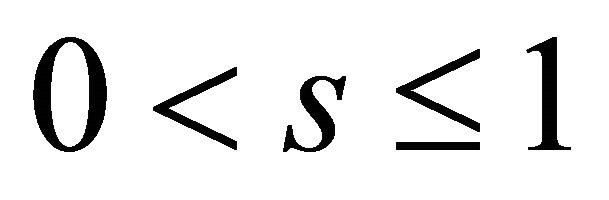 , and
, and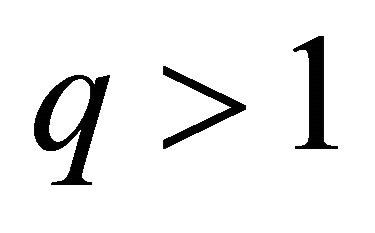 , we have
, we have
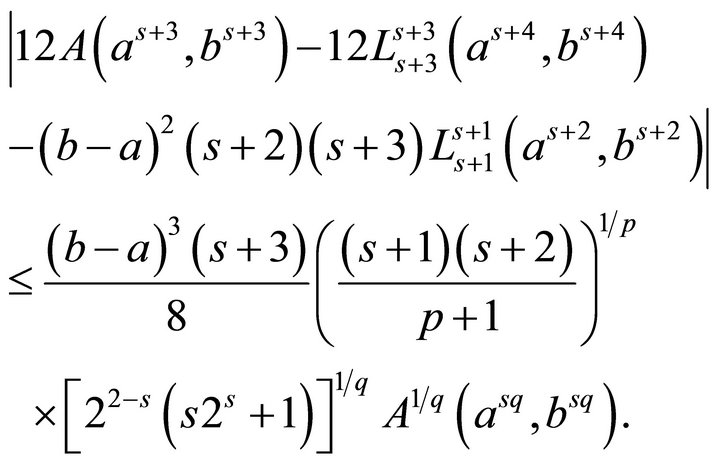 (4.4)
(4.4)
Theorem 4.3. For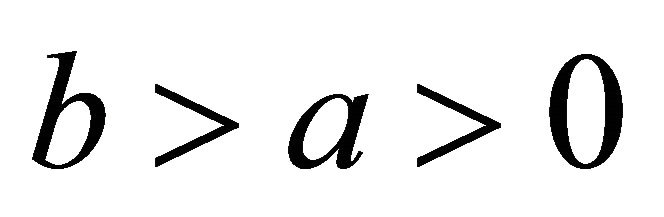 ,
, 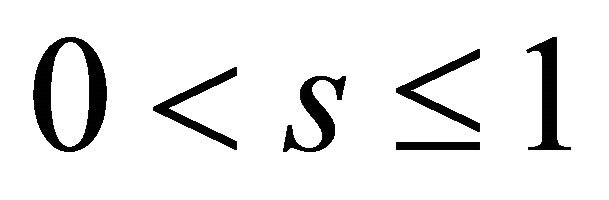 , and
, and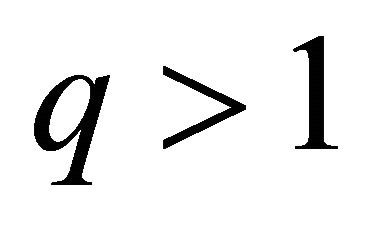 , we have
, we have

5. Acknowledgements
The first author was supported by Science Research Funding of Inner Mongolia University for Nationalities under Grant No. NMD1103.
REFERENCES
- S. S. Dragomir, J. Pecaric and L.-E. Persson, “Some Inequalities of Hadamard Type,” Soochow Journal of Mathematics, Vol. 21, No. 3, 1995, pp. 335-341.
- H. Hudzik and L. Maligranda, “Some Remarks on s-Convex Functions,” Aequationes Mathematicae, Vol. 48, No. 1, 1994, pp. 100-111.
- S. S. Dragomir and R. P. Agarwal, “Two Inequalities for Differentiable Mappings and Applications to Special Means of Real Numbers and to Trapezoidal Formula,” Applied Mathematics Letters, Vol. 11, No. 5, 1998, pp. 91-95. doi:10.1016/S0893-9659(98)00086-X
- C. E. M. Pearce and J. Pečarić, “Inequalities for Differentiable Mappings with Application to Special Means and Quadrature Formulae,” Applied Mathematics Letters, Vol. 13, No. 2, 2000, pp. 51-55. doi:10.1016/S0893-9659(99)00164-0
- U. S. Kirmaci, “Inequalities for Differentiable Mappings and Applications to Special Means of Real Numbers and to Midpoint Formula,” Applied Mathematics and Computation, Vol. 147, No. 1, 2004, pp. 137-146. doi:10.1016/S0096-3003(02)00657-4
- U. S. Kirmaci, M. K. Bakula, M. E. Ozdemir and J. Pecaric, “Hadamard-Type Inequalities for s-Convex Functions,” Applied Mathematics and Computation, Vol. 193, No. 1, 2007, pp. 26-35. doi:10.1016/j.amc.2007.03.030
- M. Alomari and S. Hussain, “Two Inequalities of Simpson Type for Quasi-Convex Functions and Applications,” Applied Mathematics E-Notes, Vol. 11, 2011, pp. 110- 117.
- R.-F. Bai, F. Qi and B.-Y. Xi, “Hermite-Hadamard Type Inequalities for the mand (α, m)-Logarithmically Convex Functions,” Filomat, Vol. 27, No. 1, 2013, 1-7.
- S.-P. Bai, S.-H. Wang and F. Qi, “Some Hermite-Hadamard Type Inequalities for n-Time Differentiable (α, m)-Convex Functions,” Journal of Inequalities and Applications, 2013, in Press.
- W.-D. Jiang, D.-W. Niu, Y. Hua and F. Qi, “Generalizations of Hermite-Hadamard Inequality to n-Time Differentiable Functions Which Are s-Convex in the Second Sense,” Analysis (Munich), Vol. 32, No. 3, 2012, pp. 209- 220. doi:10.1524/anly.2012.1161
- F. Qi, Z.-L. Wei and Q. Yang, “Generalizations and Refinements of Hermite-Hadamard’s Inequality,” The Rocky Mountain Journal of Mathematics, Vol. 35, No. 1, 2005, pp. 235-251. doi:10.1216/rmjm/1181069779
- S.-H. Wang, B.-Y. Xi and F. Qi, “On Hermite-Hadamard Type Inequalities for (α, m)-Convex Functions,” International Journal of Open Problems in Computer Science and Mathematics, Vol. 5, No. 4, 2012, in Press.
- S.-H. Wang, B.-Y. Xi and F. Qi, “Some New Inequalities of Hermite-Hadamard Type for n-Time Differentiable Functions Which Are m-Convex,” Analysis (Munich), Vol. 32, No. 3, 2012, pp. 247-262. doi:10.1524/anly.2012.1167
- B.-Y. Xi, R.-F. Bai and F. Qi, “Hermite-Hadamard Type Inequalities for the mand (α; m)-Geometrically Convex Functions,” Aequationes Mathematicae, 2012, in Press. doi:10.1007/s00010-011-0114-x
- B.-Y. Xi and F. Qi, “Some Hermite-Hadamard Type Inequalities for Differentiable Convex Functions and Applications,” Hacettepe Journal of Mathematics and Statistics, Vol. 42, 2013, in Press.
- B.-Y. Xi and F. Qi, “Some Integral Inequalities of Hermite-Hadamard Type for Convex Functions with Applications to Means,” Journal of Function Spaces and Applications, Vol. 2012, 2012, 14 pp. doi:10.1155/2012/980438
- T.-Y. Zhang, A.-P. Ji and F. Qi, “On Integral Inequalities of Hermite-Hadamard Type for s-Geometrically Convex Functions,” Abstract and Applied Analysis, Vol. 2012, 2012, 15 pp. doi:10.1155/2012/560586
- S. S. Dragomir and C. E. M. Pearce, “Selected Topics on Hermite-Hadamard Type Inequalities and Applications,” RGMIA Monographs, Victoria University, Melbourne, 2000.
- C. P. Niculescu and L.-E. Persson, “Convex Functions and Their Applications: A Contemporary Approach (CMS Books in Mathematics),” Springer-Verlag, New York, 2005.

