Applied Mathematics
Vol.3 No.10A(2012), Article ID:24112,6 pages DOI:10.4236/am.2012.330191
Analysis of Ringing and Noise in FE and FDTD Calculated Acoustic Pulse Profiles
1School of Physics, University of the Witwatersrand, Johannesburg, South Africa
2Department of Mechanical and Process Engineering, ETH, Zurich, Switzerland
Email: arthur.every@wits.ac.za
Received July 3, 2012; revised August 6, 2012; accepted August 13, 2012
Keywords: Numerical Dispersion; Wave Field Modelling; FE; FDTD Calculations
ABSTRACT
Ringing, i.e. the emergence of an oscillatory tail behind a wave pulse as it propagates through a medium, is a pervasive artefact in FE and FDTD calculated waveforms. It is known to be a consequence of numerical dispersion arising from the discretization of the equations of motion. The use of an irregular mesh in a FE code has the further consequence of rendering the displacement field increasingly noisy with distance behind the wave front. In this paper these effects are illustrated using the commercial FE package ABAQUS with square and irregular triangular meshes to calculate the progress of a longitudinally polarized Ricker pulse along the axis of a cylindrically shaped aluminium specimen. We are able to give a precise analytical account of the evolution of ringing on the basis of a low order approximation for the dispersion relation of the discretized equations of motion. A qualitative account is provided of the generation of noise in the use of an irregular triangular mesh.
1. Introduction
Ringing, i.e. the emergence of an oscillatory tail behind a wave pulse as it propagates through a medium, is a pervasive artefact in finite element (FE) and finite difference time domain (FDTD) calculated waveforms. It is known to be a consequence of numerical dispersion arising from the discretization of the equations of motion [1]. Considerable effort has been devoted by many investigators over the years to developing strategies for reducing numerical dispersion in FE codes, see e.g. Refs. [2-5], although ringing in itself has not featured as a central issue in most of these works. The presence of noise in wave forms obtained with irregular meshes has also been noted previously [1]. Our attention has been drawn to these effects through our analysis of elastic wave propagation in a scanning probe tip [6,7], and the present paper sets out to examine these effects and explore their underlying mechanisms.
In this paper these effects are illustrated using the commercial FE package ABAQUS with square and irregular triangular meshes to calculate the progress of a longitudinally polarized Ricker pulse along the axis of a cylindrically shaped aluminium specimen. We are able to give a precise analytical account of the evolution of ringing on the basis of a low order approximation for the dispersion relation of the discretized equations of motion. A clear understanding of ringing may suggest action for mitigating its effects, or provide a useful metric for assessing dispersion.
In FE calculated waveforms based on irregular spatial meshes another pervasive artefact is the build up of noise. In a 2D (x, t) or (x, y) colour or gray scale plot, this noise to some extent resembles laser speckle, and can obscure less prominent mode conversions and other wave arrivals trailing the main pulse. The build up of noise is a cumulative effect from the quasi-random-phase scattering by the irregularly sized and shaped elements.
2. FE Calculations
To illustrate the emergence of ringing and noise in FE calculated pulse shapes we use the commercial FE package ABAQUS/Explicit [8] to obtain the time dependent velocity field in an aluminium cylinder, of length and radius both 1mm, resulting from the application of a pressure pulse 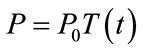 distributed uniformly over the upper surface of the cylinder, and having time dependence
distributed uniformly over the upper surface of the cylinder, and having time dependence 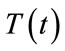 in the form of a Ricker pulse
in the form of a Ricker pulse
 (1)
(1)
where 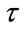 is the time constant. The Ricker pulse and its Fourier transform
is the time constant. The Ricker pulse and its Fourier transform
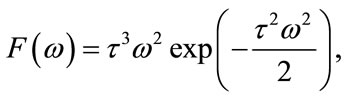 (2)
(2)
are depicted in Figure 1.
Because of the axial symmetry of the physical situation, in cylindrical coordinates the displacement field has only radial (r) and axial (z) components, and is independent of the azimuthal angle (θ). The calculations have accordingly been performed in cylindrical coordinates requiring only 2D meshing [9].
The rz domain has been meshed in two ways, by a 1000 × 1000 square mesh (spatial step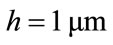 ) and by an irregular triangular mesh of approximately the same number, 106, of linear elements of area on average
) and by an irregular triangular mesh of approximately the same number, 106, of linear elements of area on average
 (a)
(a)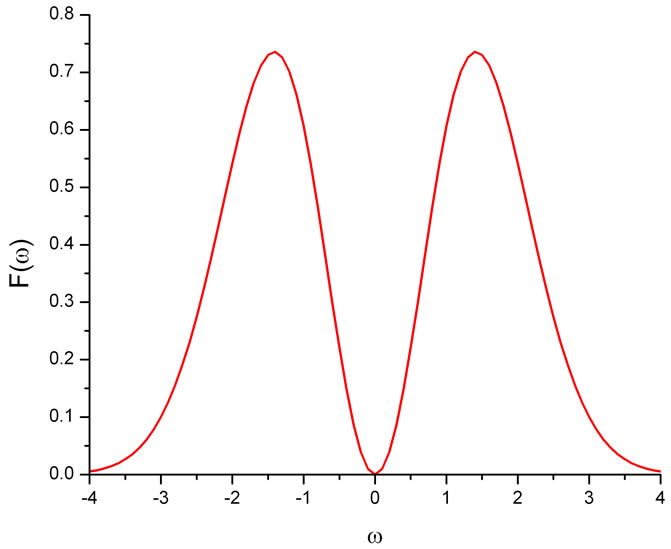 (b)
(b)
Figure 1. (a) The Ricker pulse for  = 1,
= 1, 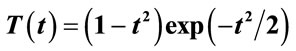 and (b) its Fourier transform
and (b) its Fourier transform  . The Ricker pressure pulse, integrated over time is zero and so delivers no net impulse.
. The Ricker pressure pulse, integrated over time is zero and so delivers no net impulse.
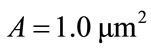 . In the second case the nodes on the boundary of the integration domain were specified, but no further control was exerted over ABAQUS regarding the meshing within the domain. Examination of the meshing that was generated showed it to contain a fairly large proportion of triangles of similar size, and more or less equilateral in shape, but there are also a significant number of triangles of other shapes and sizes. These features are illustrated in Figure 2, which depicts part of a square domain meshed into irregular triangular elements. It is not obvious what the effective value of
. In the second case the nodes on the boundary of the integration domain were specified, but no further control was exerted over ABAQUS regarding the meshing within the domain. Examination of the meshing that was generated showed it to contain a fairly large proportion of triangles of similar size, and more or less equilateral in shape, but there are also a significant number of triangles of other shapes and sizes. These features are illustrated in Figure 2, which depicts part of a square domain meshed into irregular triangular elements. It is not obvious what the effective value of 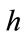 is for such a mesh, although it must scale as
is for such a mesh, although it must scale as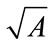 , and so we have treated h as a parameter to be determined by fitting analytic to FE calculated waveforms. A lower limit for h can reasonably be supposed to be
, and so we have treated h as a parameter to be determined by fitting analytic to FE calculated waveforms. A lower limit for h can reasonably be supposed to be 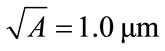 and a reasonable upper limit is the side of the average equilateral triangle,
and a reasonable upper limit is the side of the average equilateral triangle,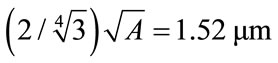 . The time step δ has been taken as 0.05 ns in the simulations with both meshes.
. The time step δ has been taken as 0.05 ns in the simulations with both meshes.
The density and Lamé elastic constants of aluminium have been taken as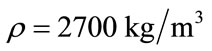 ,
, 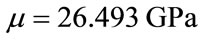 and
and , yielding longitudinal and transverse velocities
, yielding longitudinal and transverse velocities  and
and  respectively. We have taken the time constant in the Ricker pulse to be
respectively. We have taken the time constant in the Ricker pulse to be . The dominant angular frequency
. The dominant angular frequency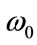 , as given by the position of the maximum in
, as given by the position of the maximum in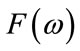 , and period
, and period 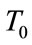 of the Ricker are related to
of the Ricker are related to 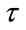 by
by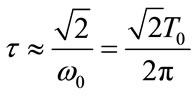 , yielding
, yielding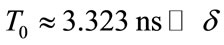 . The dominant wavelength of the longitudinal pulse launched into the specimen is
. The dominant wavelength of the longitudinal pulse launched into the specimen is 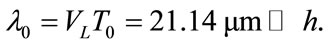 The numerical wave speed
The numerical wave speed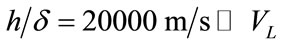 , as required for stability of the FE calculation [10].
, as required for stability of the FE calculation [10].
Figure 3 depicts the FE calculated velocity field  at
at 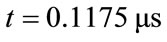 in the cylinder, resulting from the Ricker pressure pulse applied to upper surface. The calculation for (a) pertains to the square mesh, and that for (b) to the irregular triangular mesh. In addition to the main L pulse, there are circular L and T edge waves
in the cylinder, resulting from the Ricker pressure pulse applied to upper surface. The calculation for (a) pertains to the square mesh, and that for (b) to the irregular triangular mesh. In addition to the main L pulse, there are circular L and T edge waves

Figure 2. Part of a square domain meshed into irregular triangular elements.
(LEW, TEW) spreading out from the top right hand corner, the straight Head wave (HW) trailing the main L pulse and tangential to the TEW, and the Rayleigh surface wave (RW) on the upper surface following closely on the TEW. All these waves display various degrees of ringing, i.e. multiple ripples trailing the main pulse. These ripples diminish in amplitude and wavelength with distance from the main pulse. Ringing is the consequence of numerical dispersion arising from the discretization of the equations of motion in the FE code. In simple terms the higher spatial frequency Fourier components of the waveform travel slower than the lower frequency ones, and so lag behind the main arrival. Although there is no specific cut-off to the ringing, there are a finite number of ripple periods that can be discerned for each wave in Figure 3 before the signal merges into the background. This number is greater, the greater the degree of dispersion, which depends on the ratios 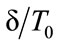 and
and , where
, where  is the characteristic period of the pressure pulse. The second ratio is smallest for the L pulse in (a). It is larger for the L pulse in (b) because of the larger effective value of h for the triangular mesh, and it is larger for the TEW because of the smaller value of the transverse wave velocity V as compared with the longitudinal velocity.
is the characteristic period of the pressure pulse. The second ratio is smallest for the L pulse in (a). It is larger for the L pulse in (b) because of the larger effective value of h for the triangular mesh, and it is larger for the TEW because of the smaller value of the transverse wave velocity V as compared with the longitudinal velocity.
The results for the irregular mesh calculation in (b) show the marked presence of noise, which builds up steadily in intensity with distance behind the wave front. Noise has an obscuring effect on the finer ripples in the wave form. A quantitative account of ringing follows in the next section, and a brief discussion of noise is provided in the last section.
3. Quantitative Account of the Ringing in FE Calculated Waveforms
We show here that ringing in FE calculated wave forms can be quantitatively accounted for very precisely on the basis of the non-linear dispersion relation resulting from the discretization of the wave equation.
A simple uniform discretization of the one-dimensional wave equation or a 2D or 3D staggered grid FD scheme such as described in Fellinger et al. [10] yields a dispersion relation of the form
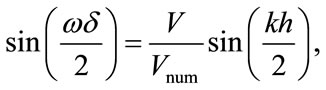 (3)
(3)
where δ and h are the time and space discretization intervals respectively, V is the physical wave speed, which we will take to be the longitudinal wave speed, 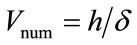 is called the numerical wave speed, ω is the angular frequency,
is called the numerical wave speed, ω is the angular frequency, 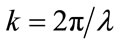 is the wave vector and λ is the wavelength. Stability of the solution of the discretized wave equation, indeed merely the ability to reproduce a signal travelling at velocity V, requires that
is the wave vector and λ is the wavelength. Stability of the solution of the discretized wave equation, indeed merely the ability to reproduce a signal travelling at velocity V, requires that
 (a)
(a)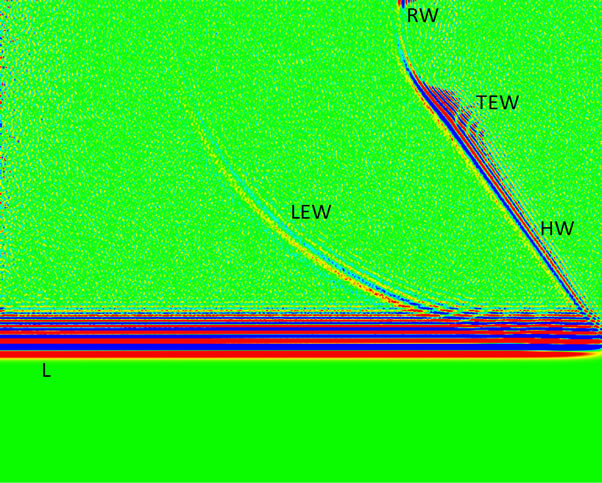 (b)
(b)
Figure 3. Colour scale representation of a “snapshot” of the velocity field vz(r, z) in the cylinder at t = 0.1175 μs resulting from the Ricker pressure pulse applied to upper surface, (a) calculation based on square mesh; (b) calculation based on irregular triangular mesh. The axis of cylinder is on the left. In addition to the main L pulse travelling vertically downwards, there are the circular L and T edge waves (LEW, TEW) spreading outwards from the top right hand corner, the straight Head wave (HW) trailing the main L pulse, and the Rayleigh surface wave (RW) on the upper surface following closely on the TEW. All of these waves exhibit oscillatory tails, and there are interesting interference effects between several of them. The irregular mesh calculation (b) shows the marked presence of noise.
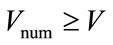 and hence
and hence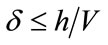 . [11] For 2D and 3D rectangular grids the constraints are
. [11] For 2D and 3D rectangular grids the constraints are
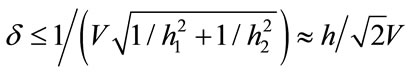
and 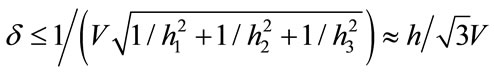 respectively, where
respectively, where ,
, 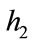 and
and 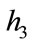 are the spatial discretization intervals in the three orthogonal directions [11], which when equal, yield the simplified results shown. In the striving for numerical accuracy at minimal computational cost it is common practice to take the shortest wavelength in the signal to be discretized by at least eight points[11] but not much more. If the highest frequency in the signal is
are the spatial discretization intervals in the three orthogonal directions [11], which when equal, yield the simplified results shown. In the striving for numerical accuracy at minimal computational cost it is common practice to take the shortest wavelength in the signal to be discretized by at least eight points[11] but not much more. If the highest frequency in the signal is , this requires taking
, this requires taking  , where
, where 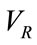 and
and 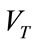 are the Rayleigh and transverse wave speeds respectively. Taking
are the Rayleigh and transverse wave speeds respectively. Taking 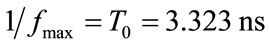 and
and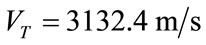 , it follows that
, it follows that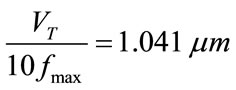 .If we consider just the L pulsethen
.If we consider just the L pulsethen .
.
Expanding the sine functions in Equation (3) to third order in their arguments, one obtains after some manipulation, the dispersion relation in the form
 (4)
(4)
The phase and group velocities derived from Equation (4) taking 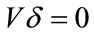 are respectively
are respectively
 (5)
(5)
Their variation with N is depicted in Figure 4.
As can be seen from Equation (4), the dispersive effects associated with δ and h are opposite in sign and tend to partially cancel. In 1D, by choosing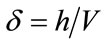 , the so-called magic time step at the limit of stability, dispersion is cancelled totally, while in 2D and 3D there can only be partial cancellation, and less so for the slower longer wavelength T modes than for the L mode.
, the so-called magic time step at the limit of stability, dispersion is cancelled totally, while in 2D and 3D there can only be partial cancellation, and less so for the slower longer wavelength T modes than for the L mode.
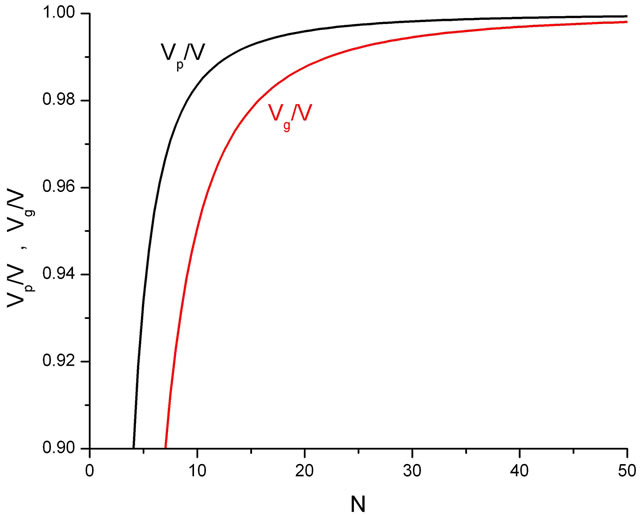
Figure 4. Variation of Vphase/V (upper curve) and Vgroup/V (lower curve) with N =λ/h.
We compare below FE simulations and analytical calculations we have done in parallel that demonstrate that ringing is a deterministic and precisely predictable effect that depends on the original pulse shape and distance travelled, and on the time and spatial intervals δ and h.
In treating the effects of dispersion on the pulse shape analytically, we consider the medium to be infinite in extent and the velocity field of the longitudinally polarized pulse launched in the specimen at 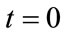 and travelling in the positive z direction to be
and travelling in the positive z direction to be
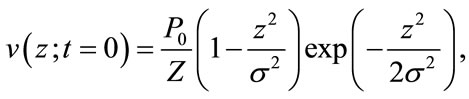 (6)
(6)
where 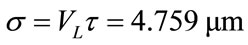
and 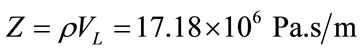
is the L wave acoustic impedance of aluminium. In our FE and analytic calculations we have set the value of .
.
The evolution of the pulse shape is determined as follows. The velocity field for the pulse launched into the solid can at time  be expressed in terms of its spatial Fourier transform
be expressed in terms of its spatial Fourier transform
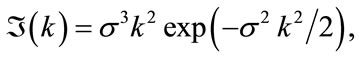 (7)
(7)
as follows
 (8)
(8)
After time t has elapsed, the pulse will have evolved to
 (9)
(9)
With change of integration variable to 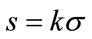 and introducing a position dependent time origin
and introducing a position dependent time origin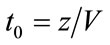 , and shifted time
, and shifted time 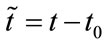 the time dependent field at point z is given by
the time dependent field at point z is given by
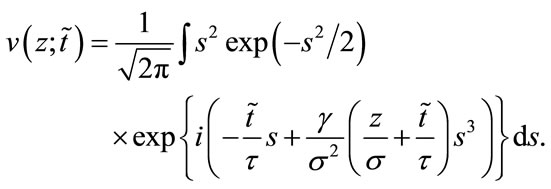 (10)
(10)
For the square mesh the values of the constants in (10) are
 ,
, 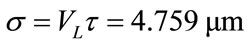
and  .
.
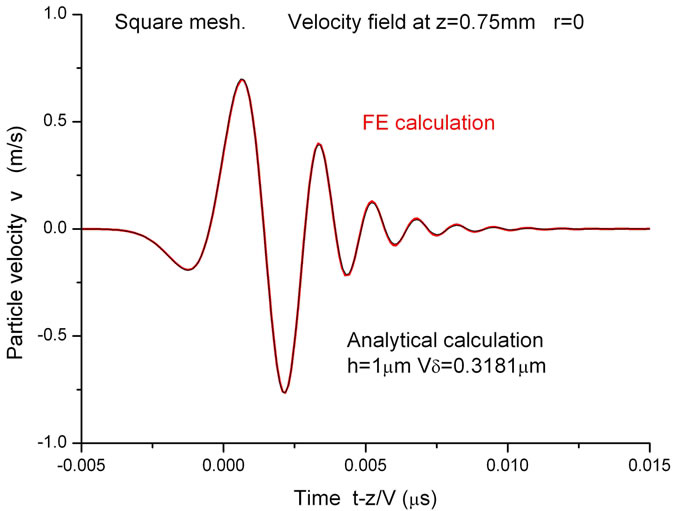
Figure 5(a) compares the regular square mesh FE calculated time dependent velocity field at a point z = 0.75 mm with the analytically calculated field, taking  and
and . As can be seen, the analytically calculated wave form is virtually indistinguishable from the FE calculated waveform.
. As can be seen, the analytically calculated wave form is virtually indistinguishable from the FE calculated waveform.
Figure 5(b) compares the linear element irregular triangular mesh FE calculated time dependent velocity field at the off-axis point z = 0.50 mm, r = 0.20 mm with the analytically calculated field for  and the adjusted value
and the adjusted value , which gives the best fit to the FE waveform for
, which gives the best fit to the FE waveform for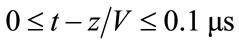 . This corresponds fairly closely to
. This corresponds fairly closely to , where A is the average area of the triangular elements, while taking
, where A is the average area of the triangular elements, while taking 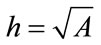 yields a waveform that does not match the FE wave form at all well.
yields a waveform that does not match the FE wave form at all well.
 (a)
(a) (b)
(b)
Figure 5. Comparison between FE calculated Ricker wave form and analytic wave forms (a) for a 1000 × 1000 regular square mesh and (b) for an irregular triangular mesh of approximately 106 linear elements, Vδ = 0.3181 μm. For (a) h = 1.0 μm, the actual spatial interval and there is no free parameter in the fit. For (b) h = 1.428 μm ≈ gives the best fit.
gives the best fit.
These results demonstrates how ringing in FE waveforms can be precisely accounted for analytically, and provides a quantitative measure, the effective value of h, for comparing the dispersive effects of different FE meshes. Table 1" target="_self"> Table 1 lists the values of h and  for the two simulations. Clearly the square grid comes out as superior to the irregular grid both in measure of dispersion.
for the two simulations. Clearly the square grid comes out as superior to the irregular grid both in measure of dispersion.
4. Noise and Attenuation in FE Waveforms
As can be seen in Figure 5(b), the fit between FE and analytic waveforms for the irregular triangular mesh calculations taking , while close initially, deteriorates markedly for
, while close initially, deteriorates markedly for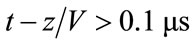 . This is because of the steady build up of noise behind the main wave arrival, which is displayed over a longer time scale in Figure 6, which is a plot of the time dependence of the difference between the FE and analytic calculated waveforms,
. This is because of the steady build up of noise behind the main wave arrival, which is displayed over a longer time scale in Figure 6, which is a plot of the time dependence of the difference between the FE and analytic calculated waveforms, 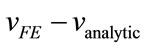 , at the point z = 0.50 mm; r = 0.20 mm. This noise, which in Figure 3(b) to some extent resembles laser speckle, tends to obscure finer features in that image. The build up of the noise is a cumulative effect from the quasi-random-phase scattering by the individual elements. The noise level is essentially zero in front of the leading Ricker pulse, and then builds up steadily in intensity with distance behind this arrival. If one excludes the region between t = 0 and
, at the point z = 0.50 mm; r = 0.20 mm. This noise, which in Figure 3(b) to some extent resembles laser speckle, tends to obscure finer features in that image. The build up of the noise is a cumulative effect from the quasi-random-phase scattering by the individual elements. The noise level is essentially zero in front of the leading Ricker pulse, and then builds up steadily in intensity with distance behind this arrival. If one excludes the region between t = 0 and ,
,
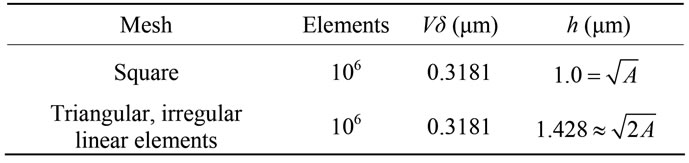
Table 1. Mesh comparisons.
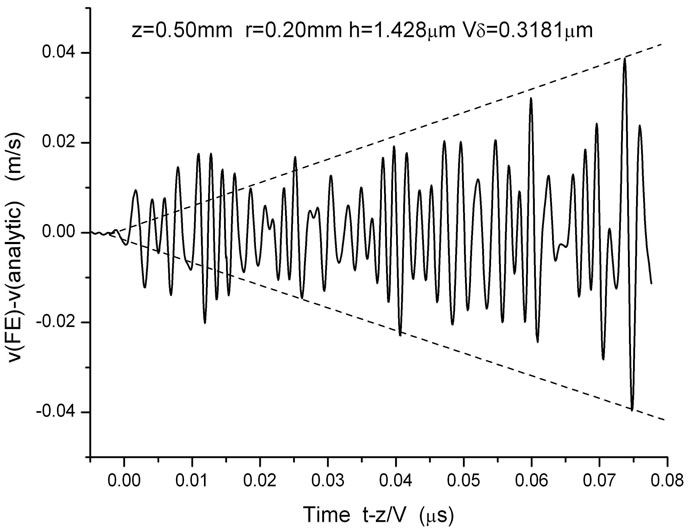
Figure 6. Time dependence of the difference between the FE and analytic calculated waveforms at the point z = 0.50 mm; r = 0.20 mm for an irregular triangular mesh of approximately 106 linear elements, taking Vδ = 0.3181 μm and h = 1.428 μm, which gives the best fit.
where the signal amplitude is large and even the small fractional difference between  and
and 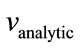 results in a fairly large value of their difference, the value of
results in a fairly large value of their difference, the value of 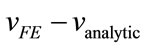 increases approximately linearly with time after the arrival
increases approximately linearly with time after the arrival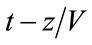 , as indicated by the dashed lines in Figure 6. This is because the space-time domain from which scattering can contribute to the noise intensity at any point and time is greater, the further that point is from the leading edge of the Ricker arrival. In the case of the regular square mesh the scattering by the individual elements is coherent and does not generate noise, and noise is absent from Figures 3(a) and 5(a). In both cases the dispersion of the pulse can be interpreted as due to the coherent component of the scattering. Similar conclusions have been reached by Huthwaite et al. [1] regarding the generation of noise in irregular mesh FE simulations. The energy routed into noise subtracts from that in the coherent field, and this will result in attenuation of the Ricker pulse. In our calculations the effect is, however, rather small, and we have not as yet established a quantitative correlation between noise and attenuation in this study.
, as indicated by the dashed lines in Figure 6. This is because the space-time domain from which scattering can contribute to the noise intensity at any point and time is greater, the further that point is from the leading edge of the Ricker arrival. In the case of the regular square mesh the scattering by the individual elements is coherent and does not generate noise, and noise is absent from Figures 3(a) and 5(a). In both cases the dispersion of the pulse can be interpreted as due to the coherent component of the scattering. Similar conclusions have been reached by Huthwaite et al. [1] regarding the generation of noise in irregular mesh FE simulations. The energy routed into noise subtracts from that in the coherent field, and this will result in attenuation of the Ricker pulse. In our calculations the effect is, however, rather small, and we have not as yet established a quantitative correlation between noise and attenuation in this study.
REFERENCES
- P. Huthwaite, F. Simonetti and M. J. S. Lowe, “On the Convergence of Finite Element Scattering Simulations,” In: D. O. Thompson and D. E. Chimenti, Eds., Review of Quantitative Nondestructive Evaluation, Melville, New York, Vol. 29, 2010, pp. 65-72.
- M. N. Guddati and B. Yue, “Modified Integration Rules for Reducing Dispersion Error in Finite Element Methods,” Computer Methods in Applied Mechanics and Engineering, Vol. 193, No. 3-5, 2004, pp. 275-287. doi:10.1016/j.cma.2003.09.010
- J. D. De Basabe and M. K. Sen, “Stability of the HighOrder Finite Elements for Acoustic or Elastic Wave Propagation with High-Order Time Stepping,” Geophysical Journal Internationa, Vol. 181, No. 1, 2010, pp. 577-590. doi:10.1111/j.1365-246X.2010.04536.x
- R. Mullen and T Belytschko, “Dispersion Analysis of Finite Element Semidiscretizations of the Two-Dimensional Wave Equation,” International Journal for Numerical Methods in Engineering, Vol. 18, No. 1, 1982, pp. 11-29. doi:10.1002/nme.1620180103
- J. Juntunen and T. D. Tsiboukis, “Reduction of Numerical Dispersion in FDTD Method through Artificial Anisotropy,” IEEE Transactions on Microwave Theory and Techniques, Vol. 48, No. 4, 2000, pp. 582-588. doi:10.1109/22.842030
- A. G. Every, I. Wenke, L. Aebi and J. Dual, “Acoustic Field Radiated into a Transversely Isotropic Solid from a Small Aperture Spherical Surface,” Ultrasonics, Vol. 51, No. 7, 2011, pp. 824-830. doi:10.1016/j.ultras.2011.04.001
- J. Bryner, J. Vollmann, L. Aebi and J. Dual, “Wave Propagation in Pyramidal Tip-Like Structures with Cubic Material Properties,” Wave Motion, Vol. 47, No. 1, 2010, pp. 33-44. doi:10.1016/j.wavemoti.2009.07.003
- ABAQUS, “A Simulia Product of Dassault Systemes,” 2002-2012. http://www.3ds.com/products/simulia/overview/
- D. Gsell, T. Leutenegger and J. Dual, “Modelling ThreeDimensional Elastic Wave Propagation in Circular Cylindrical Structures Using a Finite-Difference Approach,” Journal of the Acoustical Society of America, Vol. 116, No. 6, 2004, pp. 3284-3293. doi:10.1121/1.1625934
- P. Fellinger, R. Marklein, K. J. Langenberg and S. Klaholz, “Numerical Modelling of Elastic Wave Propagation and Scattering with EFIT—Elastodynamic Finite Integration Technique,” Wave Motion, Vol. 21, No. 1, 1995, pp. 47-66. doi:10.1016/0165-2125(94)00040-C
- F. Schubert, A. Peiffer, B. Kohler and T. Sanderson, “The Elastodynamic Finite Integration Technique for Waves in Cylindrical Geometries,” Journal of the Acoustical Society of America, Vol. 104, No. 5, 1998, pp. 2604-2614. doi:10.1121/1.423844

