Received 1 July 2015; accepted 21 July 2015; published 24 July 2015

ABSTRACT

We develop in this text a probabilistic approach to deterministic nonlinear systems. By studying the spectral properties of the Frobenius-Perron operator of a Duffing oscillator, relevant dynamic properties of the system are identified. Using the characteristics of the Dirac operator, the evolution of the probability density function is obtained for the Duffing oscillator, allowing important aspects of this system to be investigated analytically. A comparison with numerical simulation is carried out in order to validate the results obtained by the analytical approach as well as to verify the nonsymmetric features of the oscillator response.

Keywords:

Perron-Frobenius, Duffing Oscillator

1. Introduction

It is well known that nonlinear dynamic systems operating under certain conditions can display unstable be- havior and, in some cases, present bifurcations and deterministic chaos [1] . Bifurcations are associated to points of structural instability of the system in parameter space and can imply, for example, in the presence of new branches of solutions as one varies a system parameter, or in the loss of stability of some of the branches. Deterministic chaos can be characterized as a continual instability of the trajectories, whereby the system tends to explore whole areas of the phase space.

These characteristics are sometimes difficult to analyze through time histories generated by means of numeric simulations from specific initial conditions. More efficient numerical methods are required for this task de- pending on the nonlinear behavior of the system, and even then it may be very time consuming to inspect all possible combinations of different control parameters along with different initial conditions. In this scenario, a probabilistic approach can simplify the system analysis, since it can give an overview of all possible occurrences for the whole phase space at once, and for every possible initial condition [2] . This is achieved here through the use of the Frobenius-Perron operator, which describes the evolution of the probability density function (PDF) of the system, citeandrzej [3] . The PDF can be interpreted as condensing information of the likelihood of finding the system in the vicinity of any particular point of the phase space, and through the identification of how the PDF changes as a control parameter is varied, the system dynamics can be mapped in an efficient way.

In Section 2, we develop the main theory of the Frobenius-Perron operator, emphasizing the physical inter- pretation of the PDF evolution, and obtaining the evolution equation for a dynamic system described by a sys- tem of ordinary differential equations.

In Section 3, we apply the method to a classical non-linear dynamic system: a Duffing oscillator. Through the use of the Dirac operator, we obtain analytical functions for the PDF evolutions and the resulting expression for the Duffing oscillator is shown in that section.

Finally, in Section 4, other results are shown and comparisons with numerical results are carried out.

2. Probabilistic Approach to Deterministic Systems

The probabilistic approach to the investigation of dynamic systems of the form 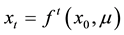begins with the construction of a probability density function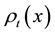, which can be interpreted as the probability at time t of finding the system near a point x of its phase space, [4] . The approach can be illustrated by the example of a system defined by the following logistic map:

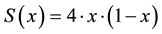
It is well known [5] that the dynamic evolution for such a system is given by:

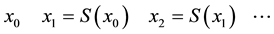
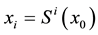
The evolution of the above map depends, therefore, on its initial condition. For example, for 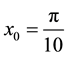the

trajectories can be seen in Figure 1.

For a small change in the initial condition 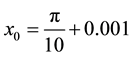the trajectories change substantially, as can be

seen in Figure 2.

In other words, this map exhibits high sensitivity to the initial conditions; as we know, this feature is a signature of chaotic behavior.

For a map like this, just looking at individual trajectories yields little information about the global dynamics of the system. The trajectories behave so erratically that no pattern can be easily identified. However, it is

possible to take the phase space and divide it into n partitions, allowing us to count the number of times the system passes through each partition.

The result of this counting procedure can be shown in a histogram. One example can be seen in Figure 3 for the same system mentioned before and for the same two different initial conditions.

These plots do not appear to be as highly sensitive to the initial conditions as the times histories presented before. In other words, this form of presenting the dynamic properties of a system seems to show a more well defined pattern, even though the system behaves in a chaotic way.

The use of probability density functions to study the dynamics of a system relies on properties of the Frobenius-Perron operator, [3] [6] [7] . This operator can be defined by means of the mathematical description of the histograms mentioned. We consider the above mentioned transformation 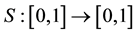and for every initial condition we make:

Considering the initial and final density states [2] one can define a characteristic function in a given interval: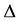

One may define 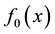as the density function for the initial states if for each interval one has:

(1)

So that for another initial condition one has:

(2)

The main goal here is to define the relation between and or, equivalently, the evolution from to.

The counter image of an interval is the set of points that will be in after the application of S, see Figure 4:

Since if and only if. Thus, in terms of the characteristic function, one has:

And therefore:

(3)

Since up to this point both and are arbitrary, and the right hand side of Equations (1) and (3) are the same, we can take, and therefore:

This is the relation between and, describing how f evolves. We now take the interval:

And differentiate with respect to x, giving:

This equation can be recast in terms of an operator as:

(4)

The equation above describes the so-called Frobenius-Perron operator.

Making use of properties of the Markov operator, as well as infinitesimal operator properties, [2] [8] , it is possible to show that the evolution of the PDF for an n dimensional system of ordinary differential equations given by:

can be described by:

(5)

where is the infinitesimal operator of the Frobenius-Perron operator, which is defined as:

(6)

3. Application to a Duffing Oscillator

The Duffing oscillator is a well known nonlinear system having as its main feature the presence of a nonlinear restoring force, [1] . This oscillator can take the form:

Rewriting the above equation in terms of phase space equations:

One has:

Now, using the Frobenius-Perron infinitesimal operator one can write the above system in terms of its pro- bability density function:.

(7)

Equation (7) represents the PDF evolution with respect to the state variables and. As presented before for the logistic map, we are here looking for a probability density function that carries information about the likelihood of finding the system near a given point in state space. In principle, we would expect that this pro- bability would be a function of and of. However, since is nothing more than the time derivative of (i.e. the rate of change of with time), a relation must exist between and the probability of finding the system near. In particular, we would expect that it is more likely to find the system in the vicinity of when is small than when it is large. But this is precisely the kind of information encapsulated by the PDF, so that we can expect to be possible to remove its explicit dependance on (since its influence must somehow be already included in the PDF).

Let us then assume that a solution for the PDF equation can be given in the following form:

(8)

where is given by:

The function represents a 3-dimensional Dirac distribution shifted by, and from the origin. Let, and be arbitrary. Choosing as a function of one removes the dependence of on, so that the idea of having the probability density function only dependent on is now inserted. Substituting Equation (8) into Equation (7) one has:

Taking yields:

For the above equation to hold the terms multiplied by must cancel each other out:

(9)

And therefore the sum of the other terms on the same side of the equation must also be zero:

(10)

Using the above equation along with Equation (9) one has:

(11)

This procedure has therefore yielded a system of two uncoupled partial differential equations defined by Equations (9) and (11). One possible solution for these equations can be formed by two exponential terms, one dependent on, and the other one coming from the term between brackets in Equation (11). Let the latter be denoted by; the following equation must then be solved in order to find:

Additionally, we note that the solution must obey appropriate boundary conditions, which might narrow down the search for a solution, and are also typical conditions imposed upon probability density functions. One of them is:

In other words, the function must be normalized in order to be visualized in a proper scale. Another boundary condition for this specific dynamical system is that for a large x, the probability must tend to zero, since it is quite unlikely to find the system in these regions of phase space (see its potential wells in Figures 5-7):

Therefore, one may choose a function, only dependent on such as so that the function takes the form:

Considering this equation, the PDF (r) takes the form:

And with and, one has the solution:

(12)

Equation (12) represents the PDF evolution for the Duffing oscillator.

4. Results for the Duffing Oscillator

Observing the behavior of the PDF over a large set of system parameters gives much information about the oscillator, and since we have a closed-form expression for the PDF evolution over time, the behavior of the Duffing oscillator can be easily mapped out. However, in order to analyze the behavior of a system in terms of its PDF we must familiarize ourselves with a new form of presenting results. These results are better understood if contrasted with classical views, such as those granted by potential well analysis or by numerical simulation.

Firstly, we vary the shape of the potential well through the changing of the parameter. In Figures 5-7 one can observe the potential wells for three different values of: 0.2, 0.5 and 1.2.

Figure 5 exhibits two well-defined valleys around. The system will therefore tend to oscillate around these two stable equilibrium points (of the unforced system).

In Figure 6 the two valleys are still present, although less pronounced than before. It can be expected that the system will still have orbits around these points, although this time one can envisage that those orbits may wander more widely in phase space than before.

In the third case (Figure 7), the two points have coalesced onto the origin, creating just one basin of attraction. It is expected that the system will oscillate around this whole region.

Using Equation (12), the PDFs for the three cases listed above were plotted in Figures 8-10. Since the value of the PDF oscillates in time (according to Equation (12)), one can chose t to be arbitrary when plotting the function. Moreover, the PDF must be normalized by its integral, making the choice of any specific time t to be irrelevant.

Figure 8 shows the PDF for. Two different areas with higher likelihood of finding the system can be seen around. These two areas are the same areas observed in the potential wells. The PDF behaves here as expected: a low, but not zero, probability distribution at the origin, since it represents an unstable equilibrium point for, and two peaks around the two stable equilibria. However, an asymmetry was identified here, which the potential well analysis did not suggest. This feature will be better investigated by numerical simu- lation, but it is also related to the phase of the excitation force which, for an initial period of time after, always forces the oscillator towards the positive side of the phase space.

In Figure 9, one can see the two areas around now presenting lower values for the PDF. However, there is still some area under the curve in these regions, as well as the asymmetry observed before. In Figure 10, the PDF is seen to be more uniformly distributed around the origin, and with boundaries defined by, exactly the same area observed in the potential well.

As mentioned above, the results for the PDF can also be compared with those obtained by numerical simu- lation. Here have we solved the equations of motion numerically for a finite number of initial conditions. The phase space was divided into n partitions, and a histogram was built based on the number of times that the time- sampled system state fell into each of the n partitions. The results as displayed in Figures 11-13.

It is clear that the same shapes noted before for the PDF curve reappear here. For, the same asymmetry between the two attractors can be observed.

Figure 12 and Figure 13 display progressive uniformity of the occurrences around the origin, a feature that was also identified in the PDF curve and in the potential wells.

Although the solution does not show a straightforward relation between the PDF and the system phase velocity, such relation can be observed in the PDF plots. This can be interpreted as the fact that the lower the phase velocity of the system at a specific phase space area, the higher the likelihood of finding the system there. The system will spend a relatively short period of time over an area where it presents a higher phase velocity. That was the reasoning behind the simplification adopted in the solution, and it has turned out to be in good agreement with the numerical results. Another example of that can be shown by observing the occurrences histogram obtained by numeric simulation in a three-dimensional graph, including also the velocity as another axis. Such a plot can be seen in Figure 14 for, for one set of initial conditions. It can be seen that the histogram remains largely unchanged, preserving the two areas with high probability, and relative small values for other areas. The asymmetry previously noticed is still present in the plot. In other words, it seems that the PDF can indeed be constructed without an explicit relation with the system phase velocity.

5. Conclusions

A probabilistic approach for the analysis of the well-known deterministic Duffing oscillator was described. Application of the Frobenius-Perron operator, and the use of suitable properties of the Dirac operator, yielded an analytical expression for the evolution of the system probability density function (PDF). The results of such approach were compared with conventional numerical simulations as well as potential well analysis.

The probabilistic approach described in this work turned out to be a very expedient method of analysis. Because it furnished an analytical expression for the PDF, different scenarios of parameters could be addressed easily, and the system could be mapped out as a whole in a very robust way. Another advantage of the method is that one single PDF represents the likelihood of finding the system for all initial conditions in the chosen phase

space domain. In this way, the PDF evolution can be seen as a simple way of producing a first overall picture of the behavior of a dynamic system in one single graph.

The area of applicability of this method in dynamic analysis seems to be extensive, especially for non-linear systems. As it was showed, even for systems which present high instability in their time trajectories (and in some cases, even chaos) this approach offers an efficient way of analysis, something that would not be so easily achieved by simple numerical simulation.

Cite this paper

Jessé Rebello de SouzaJunior,Claudio GomesFernandes, (2015) Probabilistic Approach in the Investigation of the Dynamics of a Duffing Oscillator. Applied Mathematics,06,1282-1293. doi: 10.4236/am.2015.68122

References