Applied Mathematics
Vol. 3 No. 5 (2012) , Article ID: 19065 , 9 pages DOI:10.4236/am.2012.35075
Uncertainty Weight Generation Approach Based on Uncertainty Comparison Matrices*
College of Science, Guilin University of Technology, Guilin, China
Email: wangchao244@163.com
Received March 8, 2012; revised April 8, 2012; accepted April 15, 2012
Keywords: AHP; Uncertainty Theory; Uncertain Variable; Uncertainty Distribution; Uncertainty Comparison Matrix; Uncertain Variable Method
ABSTRACT
In practical application of AHP, non-deterministic factors are frequently encountered. This paper employs uncertainty theory to deal with non-deterministic factors in problems of ranking alternatives. The concepts of uncertainty comparison matrix and uncertainty weights are proposed in this paper. It also gives the uncertain variable method to calculate uncertainty weights from uncertainty comparison matrices, which can be either consistent or inconsistent. The proposed uncertain variable method (UVM) is also applicable to interval comparison matrices and fuzzy comparison matrices when they are transformed into uncertainty comparison matrices using linear uncertainty distribution or zigzag uncertainty distribution. The proposed approach is computationally efficient as it consists of solving only inverse uncertainty distribution. At the end of this paper, five numerical examples are given to illustrate the method.
1. Introduction
The Analytic Hierarchy Process (AHP) is a multicriteria decision making (MCDM) technique founded by Saaty (1977, 1980), that integrates pairwise comparison ratios into a ratio scale. In classical AHP, the decision maker is asked to supply exactly pairwise comparison ratios for each attribute in each level of the hierarchy. The comparison matrix is formed by these comparison ratios and its principal eigenvector gives the relative weights of the sub-attributes. However, due to the complexity and uncertain factors involved in real-world decision problems and the inherent subjective nature of human preference judgments, it is unrealistic and infeasible to obtain exact judgments. So there is a necessary literature which addresses the situation where the comparison ratios are imprecise judgments. A number of techniques have been developed to use such a fuzzy or interval comparison matrix to generate weights.
Many works considered such imprecise judgments as uncertainty in the stochastic or statistical context where the judgment ratio was viewed as a random variable (Vargas, 1982; Saaty and Vargas, 1987; Zahir, 1991; Stam and Duarte Silva, 1997). The earliest work in fuzzy AHP appeared in Van Laarhoven and Pedrycz (1983) [1] which compared fuzzy ratios described by triangular membership functions; Lootsma [2] employed the logarithmic least-squares method and the geometric mean method to generate fuzzy weights. Buckley [3] determined fuzzy priorities of comparison ratios whose membership functions were trapezoidal. Modifying Van Laarhoven and Pedrycz’s method (1983), Boender et al. [4] found a fallacy in the normalization procedure for generating fuzzy weights. Leung and Cao [5] proposed a fuzzy consistency definition by considering a tolerance deviation and determined fuzzy local and global weights using the extension principle. Saaty and Vargas [6] firstly presented interval judgments for the AHP method as a way to model subjective uncertainty and used a Monte Carlo simulation approach to find out weight intervals from interval comparison matrices. Wang, Yang and Xu [7] proposed a two-stage logarithmic goal programming method (TLGP) for generating weights from interval comparison matrices and it was also applied to fuzzy comparison matrices when they were transformed into interval comparison matrices using 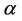 -level sets and the extension principle. Uncertainty in the preference judgments gave rise to uncertainty in the ranking of alternatives as well as difficulty in determining consistency of preferences.
-level sets and the extension principle. Uncertainty in the preference judgments gave rise to uncertainty in the ranking of alternatives as well as difficulty in determining consistency of preferences.
The imprecise comparison ratios are caused by decision makers’ subjective judgment. Unfortunately, it is not suitable to regard every non-deterministic phenomenon as random phenomenon, especially when the non-deterministic phenomenon is caused by subjective judgment. On the one hand, a lot of surveys showed that the subjective uncertainty cannot be modeled by fuzziness. On the other hand, in some works, fuzzy parameters are assumed to have known membership functions and credibility distributions. However, Atanu Sengupta and Tapan Kumar Pal [8] considered that in real-world to a decision maker (DM) it is difficult to specify the membership function or probability distribution in an ambiguous environment [8]. So some scholars point out the use of interval comparison matrices may serve the purpose better in some of the cases. But the method how to derive weights from the inconsistency of the interval comparison matrices is still subject to further investigation and the interval weights may cause the ranking reversal in the sense of definition of the degree of preference. In a word, the method of interval judgments is likely to be flawed.
Uncertainty theory, proposed by Liu [9] in 2007 and refined by Liu [10] in 2010, provides a new approach to deal with non-deterministic factors. Nowadays, based on normality, self-duality, countable subadditivity, and product measure axioms, it has become a branch of mathematics. This provides a motivation to introduce uncertainty theory into AHP. Chao Wang et al. [11] gave an uncertain decision making model. In that paper, the comparison ratios in AHP can be viewed as uncertain variable and described with uncertainty distribution. We call this decision problem model uncertain AHP when uncertain variable is brought in.
The paper is organized as follows. In Section 2, uncertainty theory is first introduced in simple word and some basic concepts and properties are given. Then, conventional-AHP ranking method is introduced. Section 3 is the main part of this paper, uncertainty comparison matrix and uncertainty weights are investigated. Section 4 presents two numerical studies to show the applications of the proposed methods. Section 5 discusses the extension of uncertain variable method to interval comparison matrices and fuzzy matrices, which are transformed into uncertainty comparison matrices using linear uncertainty distribution and zigzag uncertainty distribution respectively. Section 6 concludes this paper with a brief summary.
2. Preliminaries
2.1. Uncertainty Theory
Here, we introduce main development of uncertainty theory in different fields in simple words. Liu [12] proposed an uncertain process and addressed the definition of uncertain differential equation. In addition, uncertain programming was founded by Liu [13] in 2009 and re- fined by Liu [10]. Gao [14] proposed the Delphi method for estimating uncertainty distribution. Liu [15] introduced an uncertain statistics and gave the leastsquares method for estimating uncertainty distribution. Gao et al. [16] discussed Liu’s inference rule with multiple antecedents and with multiple if-then rules in 2010. To explore the recent developments of uncertainty theory, readers may consult Liu [10,15].
Now we introduce some concepts and theorems of uncertainty theory used throughout of this paper.
Definition 2.1 (Liu [9]) The set function 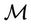 is called an uncertain measure if it satisfies the normality, selfduality, and countable subadditivity axioms.
is called an uncertain measure if it satisfies the normality, selfduality, and countable subadditivity axioms.
Axiom 1. (Normality Axiom) 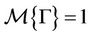 for the universal set
for the universal set 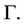
Axiom 2. (Self-Duality Axiom) 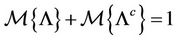 for any event
for any event 
Axiom 3. (Countable Subadditivity Axiom) For every countable sequence of events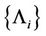 , we have
, we have
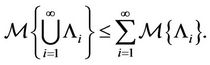
Definition 2.2 (Liu [9]) An uncertain variable is a measurable function  from an uncertainty space
from an uncertainty space  to the set of real numbers, i.e., for any Borel set of real numbers, the set
to the set of real numbers, i.e., for any Borel set of real numbers, the set
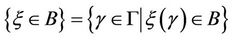
is an event (see Figure 1).
Definition 2.3 (Liu [9]) Suppose 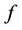 is a measurable function, and
is a measurable function, and 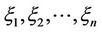 are uncertain variables on
are uncertain variables on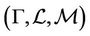 . Then
. Then 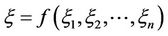 is an uncertain variable defined as
is an uncertain variable defined as
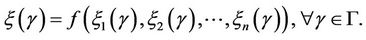
Definition 2.4 (Liu [9]) The uncertainty distribution 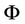 of an uncertain variable
of an uncertain variable 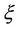 is defined by
is defined by
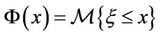
for any real number  (see Figures 2, 3).
(see Figures 2, 3).
Some special uncertainty distributions are widely used.
Linear uncertainty distribution  is given by
is given by
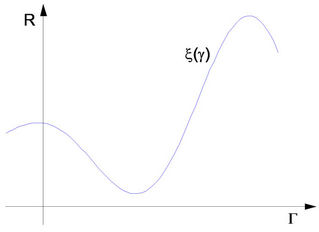
Figure 1. An uncertain variable.
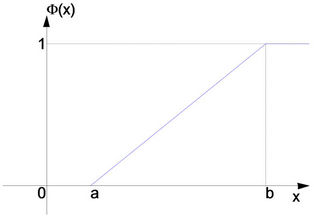
Figure 2. A linear uncertainty distribution.
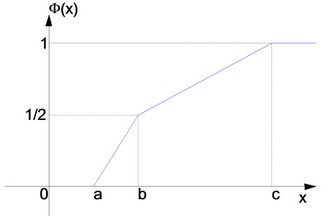
Figure 3. A zigzag uncertainty distribution.
where  and
and 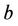 are real numbers with
are real numbers with  (see Figure 2).
(see Figure 2).
Zigzag uncertainty distribution 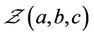 is given by
is given by
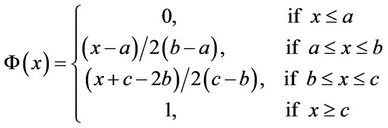
where 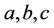 are real numbers with
are real numbers with 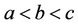 (see Figure 3).
(see Figure 3).
Definition 2.5 (Liu [15]) An uncertainty distribution 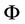 is said to be regular if its inverse function
is said to be regular if its inverse function  exists and is unique for each
exists and is unique for each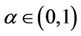 .
.
Definition 2.6 (Liu [15]) Let  be an uncertain variable with regular uncertainly distribution
be an uncertain variable with regular uncertainly distribution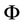 . Then the inverse function
. Then the inverse function  is called the inverse uncertainty distribution of
is called the inverse uncertainty distribution of .
.
Note that the inverse uncertainty distribution 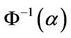 is well defined on the open interval
is well defined on the open interval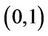 . If needed, we may extend the domain via
. If needed, we may extend the domain via
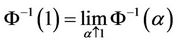 . It is easy to verify that an inverse uncertainty distribution is a monotone increasing function on
. It is easy to verify that an inverse uncertainty distribution is a monotone increasing function on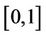 .
.
Theorem 2.1 (Liu [10]) Let 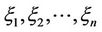 be independent uncertain variables with regular uncertainty distribution
be independent uncertain variables with regular uncertainty distribution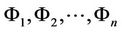 , respectively. If
, respectively. If  is a strictly increasing function, then
is a strictly increasing function, then
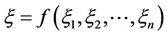
is an uncertain variable with inverse uncertainty distribution
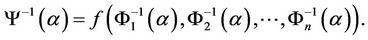
2.2. Conventional-AHP
There are many methods to obtain the weights of the alternatives, such as sum method, root method, eigenvalue method, least-squares method and logarithm least-squares method and so on. Saaty suggested that the inconsistency in Conventional-AHP, where the Right Eigenvector Method (EVM, such as (1)) is used as priorization procedure
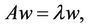 (1)
(1)
where 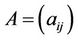 is the positive pairwise comparison matrix whose entries are chosen in the set of values
is the positive pairwise comparison matrix whose entries are chosen in the set of values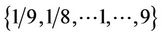 .
.  is used to test the consistency of
is used to test the consistency of , and
, and 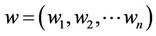 is the vector of weights of the attributes we need when it is normalized.
is the vector of weights of the attributes we need when it is normalized.
Crawford and Williams [17] suggested for the Row Geometric Mean Method (RGMM), one of the most extended AHP’s priorization procedure, a measure of the inconsistency based on stochastic properties of a subjacent model. Crawford and Williams considered the priorization procedure known as the RGMM, where the priorities (without the normalization factor) are given by
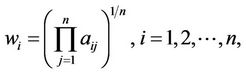 (2)
(2)
where 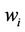 is the weight of the
is the weight of the 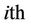 attribute.
attribute.
Suppose weights for upper-level and lower-level alternatives have all been obtained, then 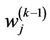 (
(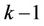 is the
is the  level of hierarchy) is the weight of criterion
level of hierarchy) is the weight of criterion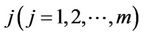 , and
, and  is the weight of alternative
is the weight of alternative 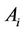 with respect to the criterion
with respect to the criterion
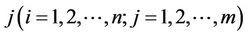 .
.
The global weight for each alternative can be generated by repeating the above synthesis processes until reaching the top level, which represents the goal of decision analysis.
3. Uncertain AHP
3.1. Basic Concepts
In some applications, different kinds of uncertainties are frequently encountered and must be taken into account. In order to determine the uncertain AHP, we give the following fundamental concepts.
Definition 3.1 An uncertainty ratio  is an inexact number representing the ratio for the relative importance of the
is an inexact number representing the ratio for the relative importance of the  subelement over the
subelement over the 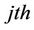 subelement, and its value takes from the interval
subelement, and its value takes from the interval  with an uncertainty distribution
with an uncertainty distribution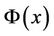 , e.g.,
, e.g.,

Definition 3.2 An 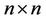 uncertain matrix is a measurable function from an uncertainty space
uncertain matrix is a measurable function from an uncertainty space 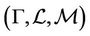 to the set of
to the set of 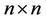 real matrix.
real matrix.
Definition 3.3 Let 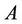 be an uncertainty comparison matrix of order
be an uncertainty comparison matrix of order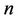 , whose entries are uncertainty distributions
, whose entries are uncertainty distributions  of uncertainty ratios
of uncertainty ratios , then the uncertainty comparison is denoted by
, then the uncertainty comparison is denoted by
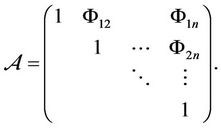
Since uncertainty distributions 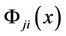
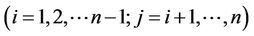 of inverse uncertainty ratios
of inverse uncertainty ratios 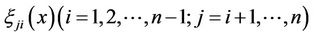 cannot be easily determined in the sense of Definition 2.4. So, in this paper, we just need to obtain the uncertainty distributions of upper triangular uncertainty ratios, the lower triangular uncertainty ratios can be obtained by
cannot be easily determined in the sense of Definition 2.4. So, in this paper, we just need to obtain the uncertainty distributions of upper triangular uncertainty ratios, the lower triangular uncertainty ratios can be obtained by
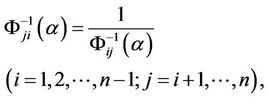 (3)
(3)
where  is the uncertain measure (confidence level) with
is the uncertain measure (confidence level) with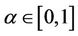 .
.
Definition 3.4 We call 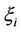 an uncertainty weight if it is an uncertain variable given by
an uncertainty weight if it is an uncertain variable given by , representing the weight of sub-attribute
, representing the weight of sub-attribute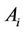 .
.
3.2. Algorithm
Essentially, the uncertainty in the human judgments gives rise to uncertainty in the ranking of alternatives as well as difficulty in determining consistency of preferences. Here in our paper we assume that the human preference judgments are not contradictory, and before proposing a new consistency measure, we focus on deriving weights from uncertainty comparison matrices. The critical procedure is that how to transform the uncertain variables into crisp numbers. Hence inverse uncertainty distribution plays an important role in this paper.
Let 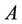 be an uncertainty comparison matrix of order
be an uncertainty comparison matrix of order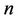 , whose entry
, whose entry 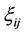 has an uncertainty distribution
has an uncertainty distribution . Liu [15] proposed the concept of strictly increasing function of uncertain variables. A real-valued function
. Liu [15] proposed the concept of strictly increasing function of uncertain variables. A real-valued function 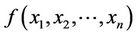 is said to be strictly increasing if
is said to be strictly increasing if
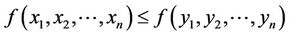
whenever 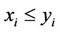 for
for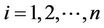 , and
, and

whenever 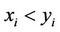 for
for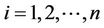 .
.
We express Equation (2) as
 (4)
(4)
then 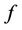 is a strictly increasing function.
is a strictly increasing function.
Proof. Apparently,
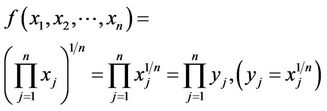
where 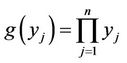 is a strictly increasing function and
is a strictly increasing function and 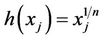 is a strictly increasing function, so the composite function
is a strictly increasing function, so the composite function  is a strictly increasing function of uncertain variables
is a strictly increasing function of uncertain variables .
.
By the Theorem 2.1, we know that
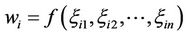
is an uncertain variable with inverse uncertainty distribution
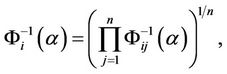 (5)
(5)
where 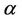 is the uncertain measure (confidence level with
is the uncertain measure (confidence level with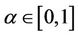 ).
).
The synthesis of weights is analogous to that proposed by Saaty in conventional-AHP, especially in this paper, the procedure of synthesis is carried out with a certain confidence level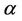 . We consider the weights acceptable when the ranking order does not alter if
. We consider the weights acceptable when the ranking order does not alter if . Otherwise the uncertainty comparison matrices will be modified.
. Otherwise the uncertainty comparison matrices will be modified.
4. Numerical Examples
In this section, we offer two numerical examples that are solved using the proposed uncertain variable method. The uncertainty distributions are obtained by Delphi method. Comparison with other existing procedures will also be made whenever possible.
Example 1 The problem is about a government agency’s goal (G) to rank chemicals A1, A2, A3 in terms of their level of harm to the environment. The goal is affected by three criteria with criterion C1: Air, C2: Water, and C3: Soil, see Figure 4.
For the above problem, we get the uncertainty distribution by Delphi method following the steps:
Q1: What do you think is the minimum ratio criterion 1 (Air) over criterion 2 (Water)?
A1: 1. (an expert’s experimental data 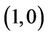 is acquired ).
is acquired ).
Q2: What do you think is the maximum ratio criterion 1 (Air) over criterion 2 (Water)?
A2: 2. (an expert’s experimental data 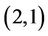 is acquired).
is acquired).
Where 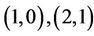 represents
represents 
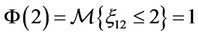 respectively. So the uncertainty ratio
respectively. So the uncertainty ratio 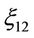 has an uncertainty distribution
has an uncertainty distribution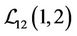 , and the uncertainty comparison matrices for the three criteria as well and for the three alternatives are obtained by Delphi and summarized in Table 1. The proposed uncertain variable method was used to generate both local and global priorities. By the Equations (3) and (5), the results are reported in Table 2, where the global weights are obtained by the procedure showed in Section 2.2.2 and expressed in Figure 5. To yield a complete ranking to help the government agency control the chemicals. From the Table 2 and Figure 5, it is clear that A1 is the most harmful chemicals because the three chemicals are ranked as
, and the uncertainty comparison matrices for the three criteria as well and for the three alternatives are obtained by Delphi and summarized in Table 1. The proposed uncertain variable method was used to generate both local and global priorities. By the Equations (3) and (5), the results are reported in Table 2, where the global weights are obtained by the procedure showed in Section 2.2.2 and expressed in Figure 5. To yield a complete ranking to help the government agency control the chemicals. From the Table 2 and Figure 5, it is clear that A1 is the most harmful chemicals because the three chemicals are ranked as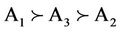 . The ranking is credible with confidence level
. The ranking is credible with confidence level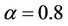 .
.
Example 2 Consider a problem about a supermarket to rank the criteria in terms of customer requirements. The goal is impacted by five criteria with criterion C1—Corporate Image, C2—Customer Except, C3—Goods, C4— Shopping Environment, and C5—Service Quality. Figure 6 shows the example of a two-level hierarchy for customer requirements.

Figure 4. Hierarchy structure in Example 1.

Table 1. Uncertainty comparison matrices in Example 1.

Table 2. Local and global priorities with confidence level. α = 0.8 in Example 1.

Figure 5. Preference relations in Example 1.
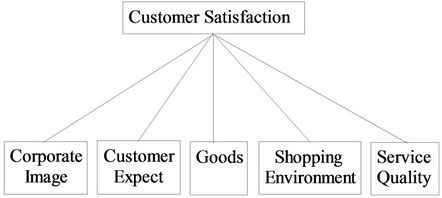
Figure 6. Hierarchy structure in Example 2.
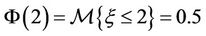 , respectively. Assume that uncertain ratio
, respectively. Assume that uncertain ratio 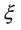 has a zigzag uncertainty distribution
has a zigzag uncertainty distribution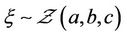 , so
, so  has an uncertainty distribution
has an uncertainty distribution . By using the questionnaire survey, the uncertainty comparison matrices are expressed as A1: 1/2. (an expert’s experimental data
. By using the questionnaire survey, the uncertainty comparison matrices are expressed as A1: 1/2. (an expert’s experimental data 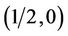 is acquired).
is acquired).
Q2: What do you think is the maximum ratio criterion 1 over criterion 2?
A2: 4. (an expert’s experimental data 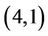 is acquired).
is acquired).
Q3: What do you think is the most possible ratio criterion 1 over criterion 2?
A3: 2. (an expert’s experimental data 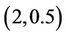 is acquired).
is acquired).
where 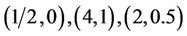 represents
represents
 ,
,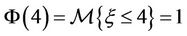 ,
,
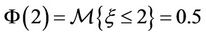 , respectively. Assume that uncertain ratio
, respectively. Assume that uncertain ratio 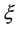 has a zigzag uncertainty distribution
has a zigzag uncertainty distribution , so
, so 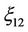 has an uncertainty distribution
has an uncertainty distribution . By using the questionnaire survey, the uncertainty comparison matrices are expressed as
. By using the questionnaire survey, the uncertainty comparison matrices are expressed as
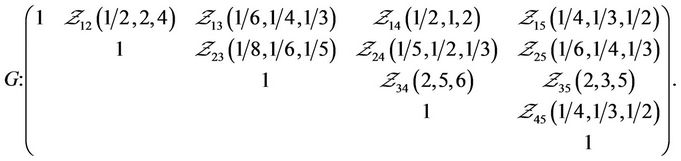
By the Equations (3) and (5), uncertainty weights are showed in Table 3 and a directed diagram is depicted in Figure 7. With the uncertain measure 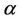 (confidence level), the ranking is deterministic rather than to a degree of preference in Wang, Yang and Xu [7]. It is clear that uncertain variable method is easier than other existing
(confidence level), the ranking is deterministic rather than to a degree of preference in Wang, Yang and Xu [7]. It is clear that uncertain variable method is easier than other existing
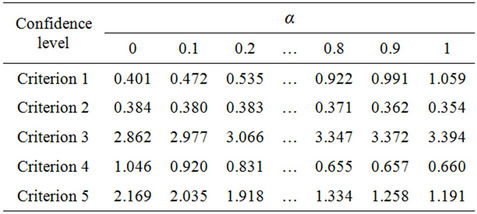
Table 3. Uncertainty weights in example 2.

Figure 7. Preference relations in Example 2.
procedures to derive priorities. The final ranking is therefore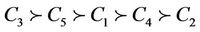 , if confidence level
, if confidence level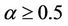 . Certainly we consider the ranking acceptable.
. Certainly we consider the ranking acceptable.
5. Extension of the Uncertain Variable Method to Interval and Fuzzy Comparison Matrices
We deal with in this section interval comparison matrices and fuzzy comparison matrices using the proposed uncertain variable method. The ranking approach for uncertainty comparison matrices discussed in Section 3 will also be extended to handle interval ranking.
Here we also introduce a method how to transform an interval into an uncertain variable has an uncertainty distribution.
Assume 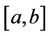 be an upper triangular interval judgment, then the corresponding uncertain variable
be an upper triangular interval judgment, then the corresponding uncertain variable 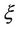 with a linear uncertainty distribution
with a linear uncertainty distribution , the lower triangular judgments can be obtained by Equation (3).
, the lower triangular judgments can be obtained by Equation (3).
Example 3 Consider the examples given by Wang, Yang and Xu [18], 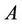 is an interval comparison matrix,
is an interval comparison matrix,
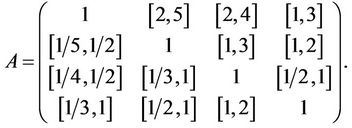
So an uncertainty comparison matrix can be expressed as

It has been known that 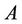 is a consistent interval comparison matrix (given by [18]), so we can directly use the Equations (3) and (5). Table 4 shows the weights with different confidence levels, from which it is clear that criterion 1 is the most important because its weight is greater than weights of all the other criteria with
is a consistent interval comparison matrix (given by [18]), so we can directly use the Equations (3) and (5). Table 4 shows the weights with different confidence levels, from which it is clear that criterion 1 is the most important because its weight is greater than weights of all the other criteria with . To provide a complete ranking order for the four uncertainty weights, a directed diagram is depicted in Figure 8, from which it is quite clear that the ranking order is
. To provide a complete ranking order for the four uncertainty weights, a directed diagram is depicted in Figure 8, from which it is quite clear that the ranking order is , which is same as rankings (
, which is same as rankings ( ) given by WangYang and Xu [18] using TLGP, but our ranking order provides the information about confidence level of preference, which reflects uncertain nature of the ranking. We can say that the ranking order
) given by WangYang and Xu [18] using TLGP, but our ranking order provides the information about confidence level of preference, which reflects uncertain nature of the ranking. We can say that the ranking order  is credible.
is credible.
Example 4 Consider the following interval compareson matrix, which was investigated by Kress [19],

The corresponding uncertainty comparison matrix is
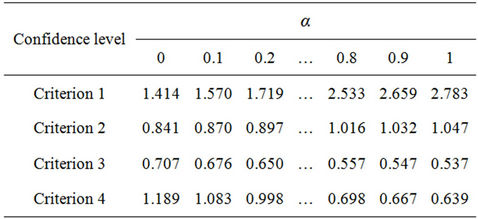
Table 4. Uncertainty weights in Example 3.
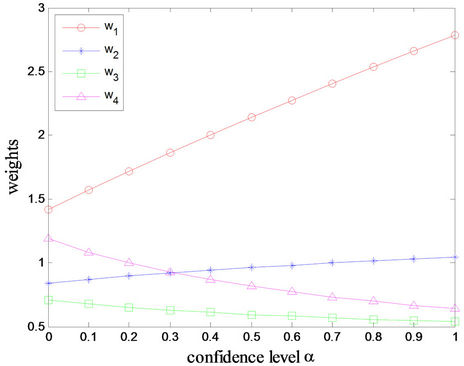
Figure 8. Preference relations in Example 3.

Kress showed that this interval comparison matrix 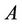 is inconsistent and many methods to derive the priorities failed. The TLGP [7] method proposed that
is inconsistent and many methods to derive the priorities failed. The TLGP [7] method proposed that  is preferred over
is preferred over  and
and  to a degree of 76.07% and 100%, respectively,
to a degree of 76.07% and 100%, respectively, 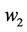 over
over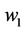 ,
, 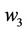 and
and 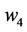 to a degree of 74.75%, 94.96% and 100%, respectively, and
to a degree of 74.75%, 94.96% and 100%, respectively, and 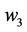 is absolutely preferred to
is absolutely preferred to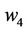 , and the final ranking is
, and the final ranking is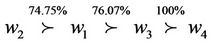 . Table 5 shows the uncertainty weights generated from the inconsistent interval comparison matrix
. Table 5 shows the uncertainty weights generated from the inconsistent interval comparison matrix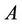 , and the corresponding confidence level, from which it can be seen that
, and the corresponding confidence level, from which it can be seen that  with all
with all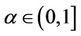 . It is same as rankings given by Wang, Yang and Xu [7] using TLGP, but our ranking provides information about the uncertain nature of the priorities, and the preference relations are much more credible. The corresponding directed diagram is depicted in Figure 9.
. It is same as rankings given by Wang, Yang and Xu [7] using TLGP, but our ranking provides information about the uncertain nature of the priorities, and the preference relations are much more credible. The corresponding directed diagram is depicted in Figure 9.
In real-world the uncertainties can also be modeled by using fuzzy numbers, we deal with fuzzy comparison matrices using the proposed uncertain variable method.

Table 5. Uncertainty weights in Example 4.
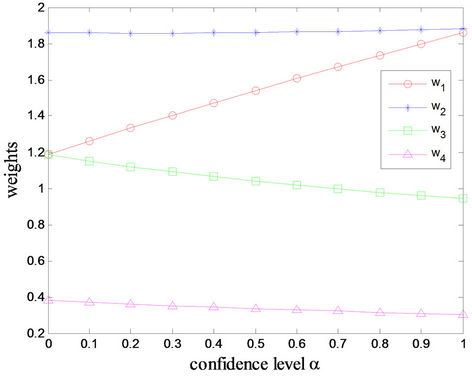
Figure 9. Preference relations in Example 4.
Let 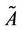 be an upper triangular fuzzy comparison matrix denoted by
be an upper triangular fuzzy comparison matrix denoted by
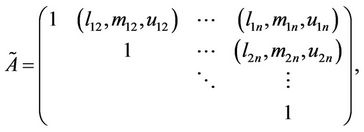
where 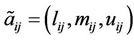
 are triangular fuzzy numbers. Here we assume uncertainty ratio
are triangular fuzzy numbers. Here we assume uncertainty ratio  has an uncertainty distribution
has an uncertainty distribution , then the fuzzy comparison matrix can be transformed into uncertainty comparison matrix
, then the fuzzy comparison matrix can be transformed into uncertainty comparison matrix

To illustrate the application of the proposed uncertain variable method to fuzzy comparison matrices, we examine the following example.
Example 5 Consider the following fuzzy comparison matrix [7]

Then the corresponding uncertainty comparison matrix is expressed by

By using the Equations (3) and (5), the uncertainty weights are derived from the above uncertainty comparison and plotted in Figure 10. It is clear that  with
with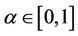 . It is same as rankings given by Wang, Yang and Xu [7] using TLGP,
. It is same as rankings given by Wang, Yang and Xu [7] using TLGP,
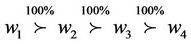 , which is the final ranking. For the other fuzzy matrices, they can be dealt with in the same method. Definitely, it is more convenient to solve the decision problems by using uncertain variable method than fuzzy comparison matrices method and interval comparison matrices method.
, which is the final ranking. For the other fuzzy matrices, they can be dealt with in the same method. Definitely, it is more convenient to solve the decision problems by using uncertain variable method than fuzzy comparison matrices method and interval comparison matrices method.
We make a summary of the methods above simply. Wang, Yang and Xu [7] pointed out the interval weights can lead to greater complexity and difficulty in compareson and ranking. They considered the judgments discrete random variables taking values from the set
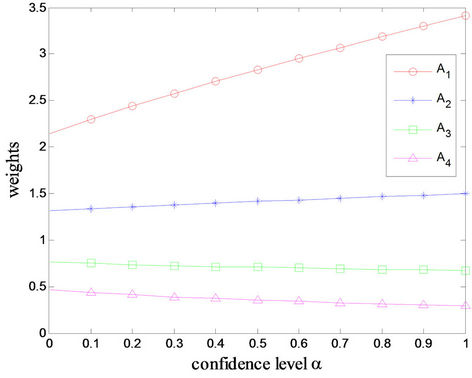
Figure 10. Preference relations in Example 5.
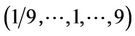 . There would be a large number of matrices being composited. For the interval matrix in Example 3, there were 432 probable combinations. And the number of matrices would be rapidly grater with the increase of order
. There would be a large number of matrices being composited. For the interval matrix in Example 3, there were 432 probable combinations. And the number of matrices would be rapidly grater with the increase of order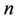 . It is a very time-consuming and laborious work to calculate all the weight vectors and find the deviation
. It is a very time-consuming and laborious work to calculate all the weight vectors and find the deviation  in [7]. MoreoverIshibuchi and Tanaka [20] used the comparison rule for interval numbers to define order relationships. Probably, this approach is prominent in analysis and comparison of interval numbers. However it fails when one interval number is nested in another one, such as
in [7]. MoreoverIshibuchi and Tanaka [20] used the comparison rule for interval numbers to define order relationships. Probably, this approach is prominent in analysis and comparison of interval numbers. However it fails when one interval number is nested in another one, such as
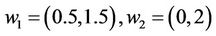 . Subsequently the degree of preference for ranks of interval weights was proposed by Wang et al. [7]. The using degree of preference may be in trouble when
. Subsequently the degree of preference for ranks of interval weights was proposed by Wang et al. [7]. The using degree of preference may be in trouble when 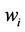 is preferred over
is preferred over 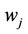 to a degree of 50% (i.e.
to a degree of 50% (i.e.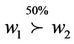 ). In that case, the ranking is still uncertain, and the ranking so obtained were likely to be flawed. However, it is difficult and unfounded to obtain the fuzzy membership function for the fuzzy method. On the contrary, the weights are precise and the ranking is deterministic with uncertain measure
). In that case, the ranking is still uncertain, and the ranking so obtained were likely to be flawed. However, it is difficult and unfounded to obtain the fuzzy membership function for the fuzzy method. On the contrary, the weights are precise and the ranking is deterministic with uncertain measure  in our paper. At the same time, uncertain measure reflects the uncertainty in ranking rather than the degree of preference.
in our paper. At the same time, uncertain measure reflects the uncertainty in ranking rather than the degree of preference.
6. Concluding Remarks
The use of pairwise comparisons to generate relative weights of criteria in multiple criteria decision analysis requires human judgments. Because of the complexity of real-world decision problems and the subjective nature of human, uncertain variable can provide a more realistic framework to deal with such uncertainty, typically, unknown constants. However, how to test the consistency of the uncertainty comparison matrices is still subject to further investigation.
In this paper, an uncertain variable method was proposed to generate weights from both consistent and inconsistent uncertainty comparison matrices. The uncertainty distributions were obtained by Delphi method or assumed to be linear distributions. The inverse distributions can transform uncertain variables into crisp numbers with a certain confidence level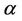 . Then generating uncertainty weights, aggregating local uncertainty weights into global uncertainty weights and ranking order can be solved easily like that in conventional-AHP. This uncertain variable method was extended to interval comparison matrices and fuzzy comparison matrices, which were transformed into uncertainty comparison matrices so that the proposed methods are also applicable to them. Five numerical examples including two hierarchical (AHP) decision problems, two interval decision problems using interval comparison matrices and one fuzzy decision problem using fuzzy comparison matrix were examined and showed the applications of the proposed method.
. Then generating uncertainty weights, aggregating local uncertainty weights into global uncertainty weights and ranking order can be solved easily like that in conventional-AHP. This uncertain variable method was extended to interval comparison matrices and fuzzy comparison matrices, which were transformed into uncertainty comparison matrices so that the proposed methods are also applicable to them. Five numerical examples including two hierarchical (AHP) decision problems, two interval decision problems using interval comparison matrices and one fuzzy decision problem using fuzzy comparison matrix were examined and showed the applications of the proposed method.
REFERENCES
- P. J. M. Van Laarhoven and W. Pedrycz, “A Fuzzy Extension of Saaty’s Priority Theory,” Fuzzy Sets and Systems, Vol. 11, 1983, pp. 229-241.
- J. Barzilai and F. A. Lootsma, “Power Relation and Group Aggregation in the Multiplicative AHP and SMART,” Journal of Multi-Criteria Decision Analysis, Vol. 6, No. 3, 1997, pp. 155-165. doi:10.1002/(SICI)1099-1360(199705)6:3<155::AID-MCDA131>3.0.CO;2-4
- J. J. Buckley, “Fuzzy Hierarchical Analysis,” Fuzzy Sets and Systems, Vol. 17, No. 3, 1985, pp. 233-247. doi:10.1016/0165-0114(85)90090-9
- C. G. E. Bonder, J. G. de Graan and F. A. Lootsma, “Multicretia Decision Analysis with Fuzzy Pairwise Comparisons,” Fuzzy Sets and Systems, Vol. 29, No. 2, 1989, pp. 133-143. doi:10.1016/0165-0114(89)90187-5
- L. C. Leung and D. Cao, “On Consistency and Ranking of Alternatives in Fuzzy AHP,” European Journal of Operational Research, Vol. 124, No. 1, 2000, pp. 102-113. doi:10.1016/S0377-2217(99)00118-6
- T. L. Saaty and L. G. Vargas, “Uncertainty and Rank Order in the Analytic Hierarchy Process,” European Journal of Operational Research, Vol. 32, No. 1, 1987, pp. 107-117. doi:10.1016/0377-2217(87)90275-X
- Y.-M. Wang, J.-B. Yang and D.-L. Xu, “A Two-Stage Logarithmic Goal Programming Method for Generating Weights from Interval Comparison Matrices,” Fuzzy Sets and Systems, Vol. 152, No. 3, 2005, pp. 475-498. doi:10.1016/j.fss.2004.10.020
- A. Sengupta and T. K. Pal, “On Comparing Interval Numbers,” European Journal of Operational Research, Vol. 127, No. 1, 2000, pp. 28-43. doi:10.1016/S0377-2217(99)00319-7
- B. Liu, “Uncertainty Theory,” 2nd Edition, SpringerVerlag, Berlin, 2007.
- B. Liu, “Uncertainty Theory: A Branch of Mathematics for Modeling Human Uncertainty,” Springer-Verlag, Berlin, 2010.
- C. Wang, L. Lin and S. Wu, “An Uncertain Decision Making Model: An Application to AHP,” International Journal of Advanced Research in Computer Science, Vol. 3, No. 2, 2012.
- B. Liu, “Fuzzy Process, Hybrid Process and Uncertain Process,” Journal of Uncertain Systems, Vol. 2, No. 1, 2008, pp. 3-16.
- B. Liu, “Theory and Practice of Uncertain Programming,” 2nd Edition, Springer-Verlag, Berlin, 2009. doi:10.1007/978-3-540-89484-1
- J. Gao, “Determine Uncertainty Distribution via Delphi Method,” The Proceedings of the First International Conference on Uncertainty Theory, Urumqi, 2010, pp. 291- 297.
- B. Liu, “Uncertainty Theory,” 4th Edition, SpringerVerlag, Berlin, 2010. doi:10.1007/978-3-642-13959-8
- X. Gao, Y. Gao and D. Ralescu, “On Liu’s Inference Rule for Uncertain Systems,” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, Vol. 18, 2010, pp. 1-11.
- G. Crawford and C. Williams, “A Note on the Analysis of Subjective Judgment Matrices,” European Journal of Operational Research, Vol. 29, 1985, pp. 387-405.
- Y.-M. Wang, J.-B. Yang and D.-L. Xu, “Interval Weight Generation Approaches Based on Consistency Test and Interval Comparison Matrices,” Applied Mathematics and Computation, Vol. 167, No. 1, 2005, pp. 252-273. doi:10.1016/j.amc.2004.06.080
- M. Kress, “Apporximate Articulation of Preference and Priority Derivation—A Comment,” European Journal of Operational Research, Vol. 52, No. 3, 1991, pp. 382-383. doi:10.1016/0377-2217(91)90174-T
- H. Ishibuchi and H. Tanaka, “Multiobjective Programming in Optimization of the Interval Objective Function,” European Journal of Operational Research, Vol. 48, No. 2, 1990, pp. 219-225. doi:10.1016/0377-2217(90)90375-L
NOTES
*This research was supported by the Guangxi Natural Science Foundation of China under the Grant No. 2011GXNSFA018149, Innovation Project of Guangxi Graduate Education under the Grant No. 2011105960202M31.

