Applied Mathematics
Vol.3 No.4(2012), Article ID:18894,6 pages DOI:10.4236/am.2012.34060
Dynamics of a Discrete Predator-Prey System with Beddington-DeAngelis Function Response
Science College, Hunan Agricultural University, Changsha, China
Email: *lxpiii168@yahoo.com.cn
Received February 7, 2012; revised March 9, 2012; accepted March 16, 2012
Keywords: Discrete; Beddington-DeAngelis Functional Response; Permanence; Global Attractivity
ABSTRACT
This paper discusses the dynamic behaviors of a discrete predator-prey system with Beddington-DeAngelis function response. We first show that under some suitable assumption, the system is permanent. Furthermore, by constructing a suitable Lyapunov function, a sufficient condition which guarantee the global attractivity of positive solutions of the system is established.
1. Introduction
Since the end of the 19th century, many biological models have been established to illustrate the evolutionary of species, among them, predator-prey models attracted more and more attention of biologists and mathematicians. There are many different kinds of predator-prey models in the literature. In 1975, Beddington [1] and DeAngelis [2] proposed the predator-prey system with the Beddington-DeAngelis functional response as follows
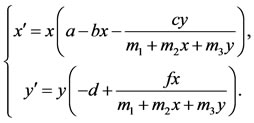 (1.1)
(1.1)
Recently, Li and Takeuchi [3] proposed the following model with both Beddington-DeAngelis functional response and density dependent predator
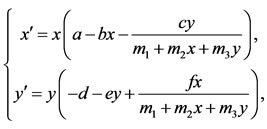 (1.2)
(1.2)
and discussed the dynamic behaviors of the model.
On the other hand, when the size of the population is rarely small or the population has non-overlaping generation, the discrete time models are more appropriate than the continuous ones. Discrete time models can also provide efficient computational models of continuous models for numerical simulations.
In [4], Qin and Liu studied the dynamic behavior of the following discrete time competitive system
 (1.3)
(1.3)
In [5], Wu and Li considered the following discrete time predator-prey system with hassell-varley type functional response
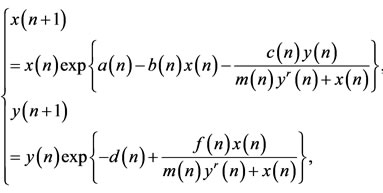 (1.4)
(1.4)
some sufficient conditions for the permanence and global attractivity of system (1.4) are obtained. For more work on this direction, one could refer to [6-14].
Based on the above discussion, in this paper, we consider the discrete analogous of (1.2), one can easily derive the discrete analogue of system (1.2), which takes the form of
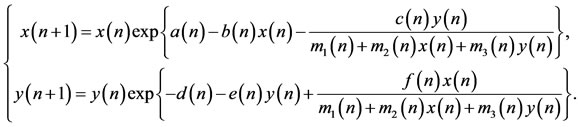 (1.5)
(1.5)
In this paper, we always assume that ,
, 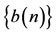 ,
,
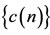 ,
, 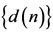 ,
, 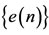 ,
, 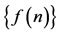 ,
, 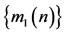 ,
,  ,
,
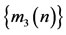 are all positive bounded sequences and
are all positive bounded sequences and
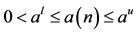 ,
, 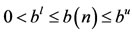 ,
,
 ,
, 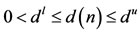 ,
,
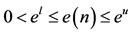 ,
,  ,
,
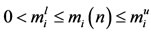 ,
, 
Here, for any bounded sequence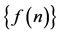 ,
,
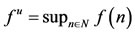 ,
, .
.
From the view point of biology, we will focus our discussion on the positive solutions of system (1.4). So it is assumed that the initial conditions of (1.4) are of the form
 . (1.6)
. (1.6)
It is easily to see that the solutions of (1.4) with the initial condition (1.5) are defined and remain positive for all .
.
2. Permanence
DEFINITION 2.1. System (1.5) is said to be permanent, if there are positive constants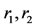 ,
, 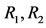 such that each positive solution
such that each positive solution 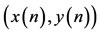 of system (1.5) satisfies
of system (1.5) satisfies
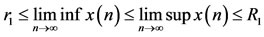 ,
,
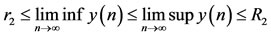 .
.
LEMMA 2.1. [6] Assume that 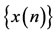 satisfies
satisfies 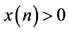 and
and
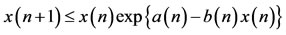
for all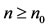 , where
, where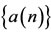 ,
, 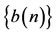 are positive sequences. Then
are positive sequences. Then
 .
.
LEMMA 2.2. [6] Assume that 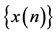 satisfies
satisfies
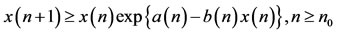
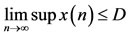 and
and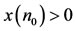 where
where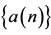 ,
, 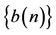 are positive sequences. Then
are positive sequences. Then
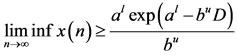 .
.
LEMMA 2.3. Assume that 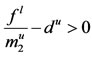 holds, then for any positive solution
holds, then for any positive solution 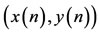 of system (1.4)one has
of system (1.4)one has
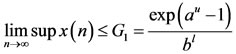
and
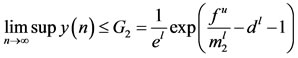 .
.
Proof. Let 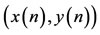 be any positive solution of system (1.5), from the first equation of (1.5), it follows that
be any positive solution of system (1.5), from the first equation of (1.5), it follows that
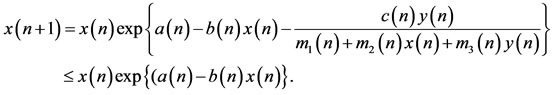
By Lemma 2.1, we obtain
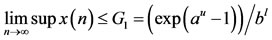 .
.
Similarly, from the second equation of (1.5), it follows that
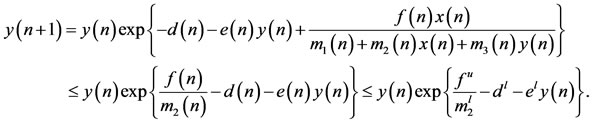
Under the assumption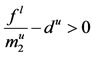 , by Lemma 2.1, we obtain
, by Lemma 2.1, we obtain
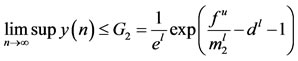 .
.
This completes the proof of Lemma 2.3.
LEMMA 2.4. Assume that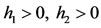 . Then for any positive solution
. Then for any positive solution 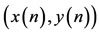 of system (1.5), one has
of system (1.5), one has
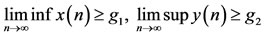 where
where
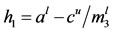 ,
,
 ,
,
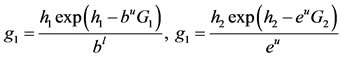 .
.
Proof. Let 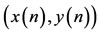 be any positive solution of system (1.5), from the first equation of (1.5), it follows that
be any positive solution of system (1.5), from the first equation of (1.5), it follows that
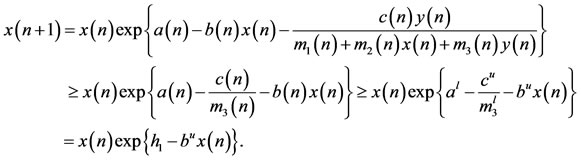
Under the assumption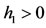 , By Lemma 2.2 and Lemma 2.3, we obtain
, By Lemma 2.2 and Lemma 2.3, we obtain
 .
.
Similarly, from the second equation of (1.5) and Lemma 2.3, it follows that

By Lemma 2.2 and Lemma 2.3, we have
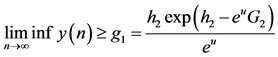 .
.
From Lemma 2.3 and Lemma 2.4, we obtain the following theorem.
THEOREM 2.1. Assume that
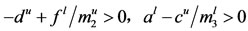 (2.1)
(2.1)
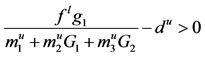 (2.2)
(2.2)
hold, then system (1.5) is permanent.
3. Global Attractivity
This section devotes to study the global attractivity of the positive solution of system (1.5).
DEFINITION 3.1. A positive solution 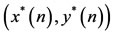 of system (1.5) is said to be globally attractive if each other positive solution
of system (1.5) is said to be globally attractive if each other positive solution 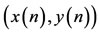 of (1.5) satisfies
of (1.5) satisfies
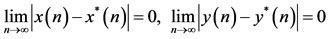 .
.
THEOREM 3.1. In addition to (2.1) and (2.2), assume further that there exist positive constants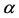 ,
, 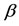 and
and  such that
such that
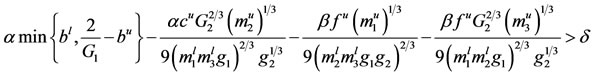 (3.1)
(3.1)
and
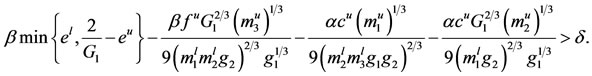 (3.2)
(3.2)
Then the positive solution of system (1.5)is globally attractive.
Proof. From (3.1) and (3.2), there exists an enough small positive constant 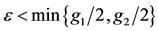 such that
such that
 (3.3)
(3.3)
and
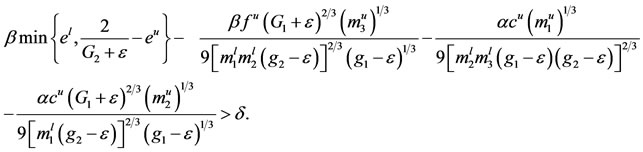 (3.4)
(3.4)
For any positive solutions  and
and  of system (1.4), it follows from Lemma 2.3 and Lemma 2.4 that
of system (1.4), it follows from Lemma 2.3 and Lemma 2.4 that
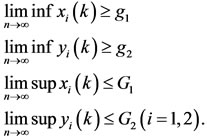 (3.5)
(3.5)
In view of (3.5), for above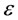 , there exists an integer
, there exists an integer 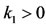 such that, for all
such that, for all ,
,
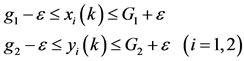 (3.6)
(3.6)
Let
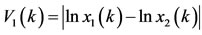 ,
,
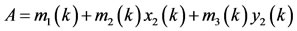 ,
,
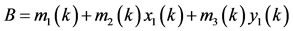 .
.
From the first equation of system (1.5), we have
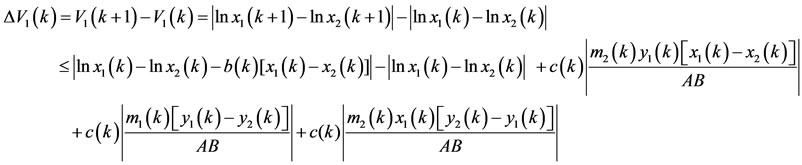
By the mean value theorem, we have
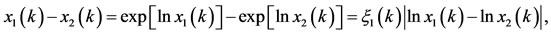 (3.7)
(3.7)
where 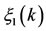 lies between
lies between 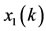 and
and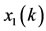 . It follows from (3.7) that
. It follows from (3.7) that
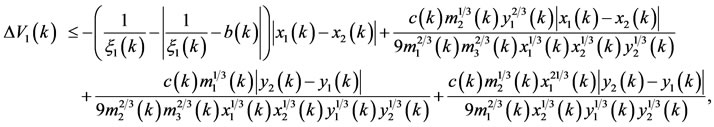
and so, for 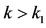
 (3.8)
(3.8)
Let
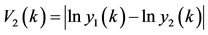 .
.
From the second equation of system (1.5), we have
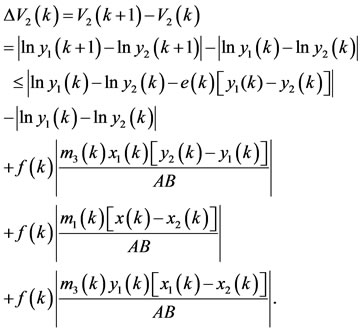
By the mean value theorem, we have
 (3.9)
(3.9)
where  lies between
lies between  and
and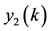 . It follows from (3.9) that
. It follows from (3.9) that
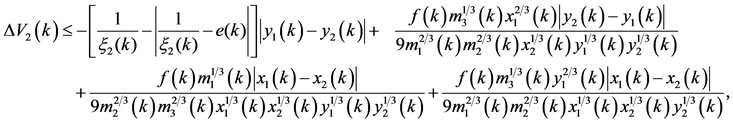
and so, for 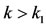
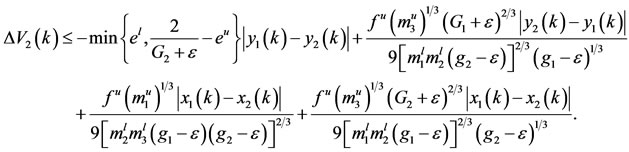 (3.10)
(3.10)
Now we define a Lyapunov function as follows:
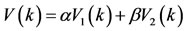 .
.
Calculating the difference of 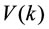 along the solution of system (1.5), for
along the solution of system (1.5), for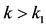 , it follows from (3.8) and (3.10) that
, it follows from (3.8) and (3.10) that
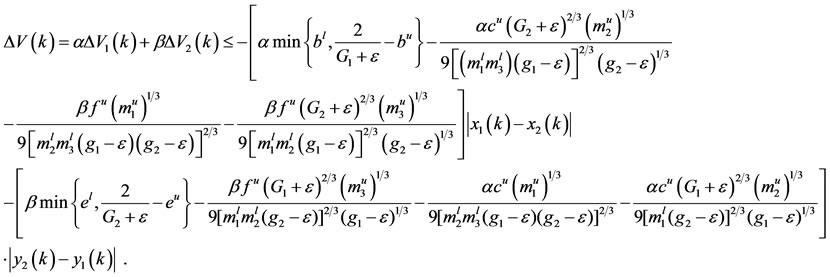
It follows from (3.3) and (3.4) that
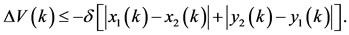
Summating both sides of the above inequalities from 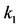 to
to , we have
, we have
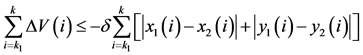 .
.
Which implies
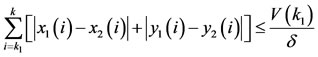 .
.
Then
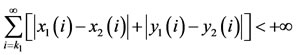 .
.
Therefore,
 .
.
That is
 .
.
This completes the proof of Theorem 3.1.
REFERENCES
- J. R. Beddington, “Mutual Interference between Parasites or Predators and Its Effect on Searching Efficiency,” Journal of Animal Ecology, Vol. 44, No. 3, 1975, pp. 331-340. doi:10.2307/3866
- D. L. DeAngelis, R. A. Goldstein and R. V. O’Neil, “A Model for Trophic Interaction,” Ecology, Vol. 56, No. 4, 1975, pp. 881-892. doi:10.2307/1936298
- H. Y. Li and Y. Takeuchi, “Dynamics of the Density Dependent Predator-Prey System with Beddington-DeAngelis Functional Response,” Journal of Mathematical Analysis and Application, Vol. 374, No. 4, 2011, pp. 644- 654. doi:10.1016/j.jmaa.2010.08.029
- W. J Qin, Z. J. Liu and Y. P. Chen, “Permanence and Global Stability of Positive Periodic Solutions of a Discrete Competitive System,” Discrete Dynamics in Nature and Society, 2009, Article ID 830537.
- R. X. Wu and Lin Li, “Permanence and Global Attractivity of Discrete Predator-Prey System with Hassell-Varley Type Functional Response,” Discrete Dynamics in Nature and Society, Applications, Vol. 299, No. 2, 2004, pp. 357- 374.
- F. Chen, “Permanence and Global Stability of Nonautonomous Lotka-Volterra System with Predator Prey and Deviating Arguments,” Applied Mathematics and Computation, Vol. 173, No. 2, 2006, pp. 1082-1100. doi:10.1016/j.amc.2005.04.035
- F. Chen, “Permanence and Global Attractivity of a Discrete Multispecies Lotka-Volterra Competition PredatorPrey Systems,” Applied Mathematics and Computation, Vol. 182, No. 1, 2006, pp. 3-12. doi:10.1016/j.amc.2006.03.026
- F. Chen, “Permanence of a Discrete n-Species Food-Chain System with Time Delays,” Applied Mathematics and Computation, Vol. 182, No. 1, 2007, pp. 719-726. doi:10.1016/j.amc.2006.07.079
- F. Chen, “Permanence for the Discrete Mutualism Model with Time Delays,” Mathematical and Computer Modelling, Vol. 47, No. 3-4, 2008, pp. 431-435. doi:10.1016/j.mcm.2007.02.023
- Y.H. Fan, W.T. Li, “Permanence for a Delayed Discrete Ratio-Dependent Predator-Prey System with Holling Type Functional Response,” Journal of Mathematical Analysis, 009, Article ID: 323065.
- L. Chen, J. Xu and Z. Li, “Permanence and Global Attractivity of a Delayed Discrete Predator-Prey System with General Holling-Type Functional Response and Feedback Controls,” Discrete Dynamics in Nature and Society, 2008, Article ID 629620.
- J. Yang, “Dynamics Behaviors of a Discrete Ratio-Dependent Predator-Prey System with Holling Type III Functional Response and Feedback Controls,” Discrete Dynamics in Nature and Society, Vol. 2008, Article ID: 186539.
- X. Li and W. Yang, “Permanence of a Discrete PredatorPrey Systems with Beddington-DeAngelis Functional Response and Feedback Controls,” 2008, Article ID 149267.
- M. Fan and K. Wang, “Periodic Solutions of a Discrete Time Nonautonomous Ratio-Dependent Predator-Prey System,” Mathematical Computer Modelling, Vol. 35, No. 9- 10, 2002, pp. 951-961. doi:10.1016/S0895-7177(02)00062-6
NOTES
*Corresponding author.

