Modern Economy
Vol.09 No.04(2018), Article ID:84092,6 pages
10.4236/me.2018.94052
Counter Cowbell Effect in a Stochastic Market: Does Subsidy Really Induce Foreign Direct Investment?
Yasunori Fujita
Keio University, Tokyo, Japan

Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 22, 2018; Accepted: April 24, 2018; Published: April 27, 2018
ABSTRACT
In the present paper, we examine if the “cowbell” attracts foreign direct investment, i.e., if the investment-attracting subsidy really induces foreign direct investment. The framework we construct is an international trade model where one firm intends a foreign direct investment under uncertainty that is expressed by geometric Brownian motion. It is revealed that contrary to the intention of the government of the host country, the cowbell does not work, that is, the investment-attracting subsidy postpones the optimal timing of foreign direct investment.
Keywords:
Counter Cowbell Effect, Foreign Direct Investment, Optimal Stopping Theory, Value of Waiting

1. Introduction
Studies on the timing of foreign direct investment, which progressed with seminal work being Buckley and Casson [1] , have entered a new phase where examination is carried out around investment-attracting measures such as tax reduction and investment subsidy, by making use of the real option theory (which is equivalent to the optimal stopping theory) that has been used to develop strategies on the timing in a stochastic economy since McDonald and Siegel [2] , Dixit [3] , Farzin, Huisman and Kort [4] etc. revealed the importance of the value of waiting. Among these studies on the foreign direct investment, notes to mention are Pennings [5] , Pennings [6] , Yu et al. [7] , Sarkar [8] , Tian [9] and so on. Pennings [5] , Pennings [6] and Yu et al. [7] showed that an investment subsidy is more efficient than a tax cut, while Sarkar [8] revealed it can be optimal to use both investment subsidy and tax cut. Tian [9] , on the other hand, demonstrated that the optimal policy for attracting investment depends on growth rate, profit’s volatility and discount rate.
In the above real-option-based models, however, prices and costs are exogenously given regardless of the amount of production, which is not necessarily sufficient framing of the problem. Thus, in the present paper, we combine the real option theory with the standard microeconomics as in Fujita [10] , Fujita [11] [12] [13] , Fujita [14] and so on. More precisely, by incorporating demand and cost functions explicitly into the real option international trade model, we examine if the “cowbell” attracts foreign direct investment, i.e., if the investment-attracting subsidy really induces foreign direct investment. The most related work is Fujita [13] that showed the backfiring effect, which means that imposing a tariff can increase exports. We can say that the counter cowbell effect shown in the present paper is a counterpart of the backfiring effect revealed in Fujita [13] .
Structure of this paper is as follows. In Section 2, we formulate the firm’s objective function after constructing a basic model to derive the equilibrium profit of the firm. Based on these analyses, Section 3 demonstrates that contrary to the intention of the government of the host country, the “cowbell” does not work, i.e., that the investment-attracting subsidy postpones the optimal timing of foreign direct investment. Concluding remarks are made in Section 4.
2. Basic Model
In this section, we construct a model that combines the real option theory with the standard microeconomics-based international trade theory. For this purpose, let us consider a firm that is planning to conduct a foreign direct investment in an intertemporal economy where time passes continuously with importance of the future diminishing with discount rate ρ. We also assume the firm takes price in each period as given, and letting x(t) denote the outputs of the firm in period t, we specify the price of the product p(t) in period t as , where A is a positive parameter that expresses market size while ε is a parameter that satisfies and expresses elasticity of demand.
Paying attention to the growing political uncertainty as in the United States of America, we assume that the variable costs increase stochastically with time, which the firm incurs after conducting the foreign direct investment with a fixed cost of K. In the following, we specify the variable costs when producing x(t)
units in period t as , where c, η and φ(t) are parameters that satisfy c > 0, η > 1 and with the following geometric Brownian motion,
, (1)
with initial value . We also assume that the foreign government provides the firm with S amount of investment-attracting subsidy when the firm conducts the foreign direct investment in period t*, while the firm, taking the investment-attracting subsidy S as given, optimizes the time of the foreign direct investment, t*, as well as the amount of the outputs in each period.
Since the firm’s profit in period t, π(t), is described as , we have its first order condition for the profit maximization in period t as , to yield the firm’s equilibrium outputs of in period t as . By combining this firm’s supply function with the above inverse demand function , we have the firm’s equilibrium output in period t as , to obtain the firm’s equilibrium profit in period t as
where . (2)
From Equation (2), we have its first derivative and second derivative with respect to φ(t) as and , respectively. Thus, by making use of Ito’s lemma, we can express the stochastic process of the firm’s profit as
, (3)
where and with initial value of .
By making use of this stochastic process of the firm’s profit, let us express the firm’s objective function to maximize in period 0, , as a function of φ*, which we define as the level of φ in period t*. For this purpose, if we let G(π(0)) denote the expected value of one unit of the firm’s profit in period t* (i.e., the expected value of ) as a function of its initial profit π(0), the general solution to G(π(0)) is expressed as
, (4)
where γ1<0 and γ2>0 are solutions to the characteristic equation . Since G(π(0)) satisfies and where π* is defined as the firm’s profit in period t*, it follows that α=0 and where for the simplification of notation, which combined with Equation (4) yields
. (5)
Thus, we can calculate the firm’s objective function to maximize in period 0 as , which is rewritten as
, (6)
by substituting and into .
3. Optimal Timing of the Foreign Direct Investment
Now, we are ready to determine the firm’s optimal timing of the foreign direct investment.
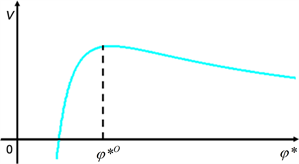
Since the model of the present paper is stochastic, the optimal timing of the foreign direct investment is expressed by the cut off level of φ*. Typical relationship between φ* and V is depicted as a one-peaked trajectory with the optimal value of φ* being φ*O on φ*-V space as in Figure 1, by assuming ε = 0.5, η = 2, γ =
2, φ(0) = 1, , K = 3 and S = 1. Thus, by differentiating Equation (6) with respect to φ* and setting it to zero, we have the firm’s optimal cut off level φ*O as
, (7)
Equation (7) implies that increase in S reduces φ*O, and since small (large) φ*O
Figure 1. Relationship between uncertainty and sum of present value of the profit.
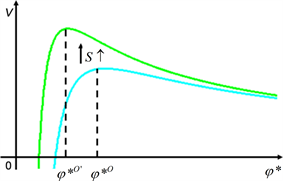
Figure 2. Effect of the subsidy on the optimal timing of FDI.
means postponement (acceleration) of the foreign direct investment, we have the following proposition.
Proposition: Investment-attracting subsidy for the foreign direct investment postpones the foreign direct investment.
This proposition shows that contrary to the intention of the government of the host country, the “cowbell” does not attract foreign direct investment, i.e., the investment-attracting subsidy does not induce foreign direct investment, since increase in the subsidy in the present model reduces the cost of foreign direct investment, to increase the value of waiting.
Graphically, Figure 2 shows that an increase in S shifts the one-peaked trajectory to the upper left, to make the optimal cut off level decrease from φ*O to φ*O'. In this figure, blue line is the same as in Figure 1, while green line is depicted by assuming S = 2 with other parameters being the same as in the blue line.
4. Conclusions
In the present paper, we examined if the “cowbell” attracts foreign direct investment, i.e., if the investment-attracting subsidy really induces foreign direct investment. The framework we invented was a model that combined the real option theory with the standard microeconomics-based international trade theory. It was revealed that contrary to the intention of the government of the host country, the “cowbell” does not work, i.e., the investment-attracting subsidy does not induce foreign direct investment. We can say that this counter cowbell effect is a counterpart of the backfiring effect Fujita [13] showed.
In order to derive explicit results, we made simplifying assumptions on demand function, cost function and stochastic motion. It is necessary to construct a general framework by relaxing those assumptions to examine the robustness of the results of the present paper. We also need to give an empirical testing of this model, in order to contribute to the progress of the international trade theory as well as the real option theory. We will take up such analyses in our next research.
Cite this paper
Fujita, Y. (2018) Counter Cowbell Effect in a Stochastic Market: Does Subsidy Really Induce Foreign Direct Investment? Modern Economy, 9, 790-795. https://doi.org/10.4236/me.2018.94052
References
- 1. Buckley, P.J. and Casson, M. (1981) The Optimal Timing of a Foreign Direct Investment. The Economic Journal, 91, 75-87. https://doi.org/10.2307/2231697
- 2. McDonald, R. and Siegel, D. (1986) The Value of Waiting to Invest. The Quarterly Journal of Economics, 101, 707-727. https://doi.org/10.2307/1884175
- 3. Dixit, A.K. (1989) Hysteresis, Import Penetration, and Exchange Rate Pass Through. Quarterly Journal of Economics, 104, 205-228. https://doi.org/10.2307/2937845
- 4. Farzin, Y.H., Huisman, K.J.M. and Kort, P.M. (1988) Optimal Timing of Technology Adoption. Journal of Economic Dynamics and Control, 22, 779-799. https://doi.org/10.1016/S0165-1889(97)00097-3
- 5. Pennings, E. (2000) Taxes and Stimuli of Investment under Uncertainty. European Economic Review, 44, 383-391. https://doi.org/10.1016/S0014-2921(98)00078-6
- 6. Pennings, E. (2005) How to Maximize Domestic Benefits from Foreign Investments: The Effect of Irreversibility and Uncertainty. Journal of Economic Dynamics and Control, 29, 873-889. https://doi.org/10.1016/j.jedc.2004.05.002
- 7. Sarkar, S. (2012) Attracting Private Investment: Tax Reduction, Investment Subsidy, or Both? Economic Modelling, 29, 1780-1785. https://doi.org/10.1016/j.econmod.2012.05.030
- 8. Yu, C.-F., Chang, T.-C. and Fan, C.-P. (2007) FDI Timing: Entry Cost Subsidy versus Tax Rate Reduction. Economic Modelling, 24, 262-271. https://doi.org/10.1016/j.econmod.2006.07.004
- 9. Tian, Y. (2018) Optimal Policy for Attracting FDI: Investment Cost Subsidy versus Tax Rate Reduction. International Review of Economics & Finance, 53, 151-159. https://doi.org/10.1016/j.iref.2017.10.018
- 10. Fujita, Y. (2007) Toward a New Modeling of International Economics: An Attempt to Reformulate an International Trade Model Based on Real Option Theory. Physica A: Statistical Mechanics and Its Applications, 383, 507-512. https://doi.org/10.1016/j.physa.2007.04.041
- 11. Fujita, Y. (2016) Optimal Amount and Timing of Investment in a Stochastic Dynamic Cournot Competition. Theoretical Economic Letters, 6, 1-6. https://doi.org/10.4236/tel.2016.61001
- 12. Fujita, Y. (2016) Value of Waiting and Excess Entry Theorem. Theoretical Economic Letters, 6, 208-213. https://doi.org/10.4236/tel.2016.62023
- 13. Fujita, Y. (2016) Backfiring Effect of Uncertain Trade Policy, Modern Economy, 7, 613-618. https://doi.org/10.4236/me.2016.75067
- 14. Fujita, Y. (2017) Does Immigration Promote the Investment of the Monopolistic Firm? Modern Economy, 8, 406-411. https://doi.org/10.4236/me.2017.83030