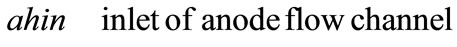Smart Grid and Renewable Energy
Vol.2 No.4(2011), Article ID:8282,7 pages DOI:10.4236/sgre.2011.24049
2D Analytical Model for Direct Ethanol Fuel Cell Performance Prediction
![]()
Fuel Cell Research Technology Group, Babol University of Technology, Babol, Iran.
Email: *s.heysiattalab@gmail.com
Received August 18th, 2011; revised October 6th, 2011; accepted October 13th, 2011.
Keywords: Analytical Model, Polarization Curve, Voltage, Current Density
ABSTRACT
Analytical models provide useful information for researchers to study fuel cell function. In this paper, it’s aimed to present a 2D analytical model for direct ethanol fuel cell (DEFC) performance. The model included equations inside diffusion layer, catalyst layer, and Ethanol cross-over through membrane, which all have been solved. Analytical model has been validated by some experimental trials. The results showed that there is proper agreement between experimental and analytical curves. Furthermore, by increasing current density, cathodic over potential will remain zero but anodic over potential will increase up to certain value. The model showed that Ethanol concentration changes almost linearly inside anode channel.
1. Introduction
Fuel cells are new power sources which produce electricity without any noise or environmental contamination. Fuel cells are used nowadays for rural, military portable and station applications [1]. Direct methanol fuel cells are one of prominent fuel cells which have high current density. Unfortunately direct methanol fuel cells have some technical problems such as methanol toxicness, expensive Pt-based catalysts, and high methanol cross over, thus, there are trends to substitute methanol with other fuels. Ethanol, acid acetic and acetaldehyde are proposed alternatives [2-5]. Recent ethanol fuel cell activities have been more experimental to date and only 1D analytical model has been proposed for DEFC so far. This model has been proposed by G. Andreadis and his colleagues by considering over potential changes inside catalyst layer [6-9]. In this paper, we try to present a 2D fully analytical model with simple consideration. With regard to Fuel cell coordinates, which have been illustrated in Figure 1, following assumptions have been made
1) Fluid flows in the steady state.
2) Fuel cell temperature is constant in the active area and chemical reaction takes place under constant temperature.
3) Reactants diffusion and transportation in catalyst layer along y direction is not considered.
4) Due to low diffusion layer thickness before its size long channel length, reactants concentration change across diffusion layer is ignored.
5) Reactants diffusion inside diffusion layer along y direction has been ignored because of low diffusion layer thickness before its length.
6) Because the thickness of membrane is so smaller than its thickness, reactants diffusion along y direction is ignored.
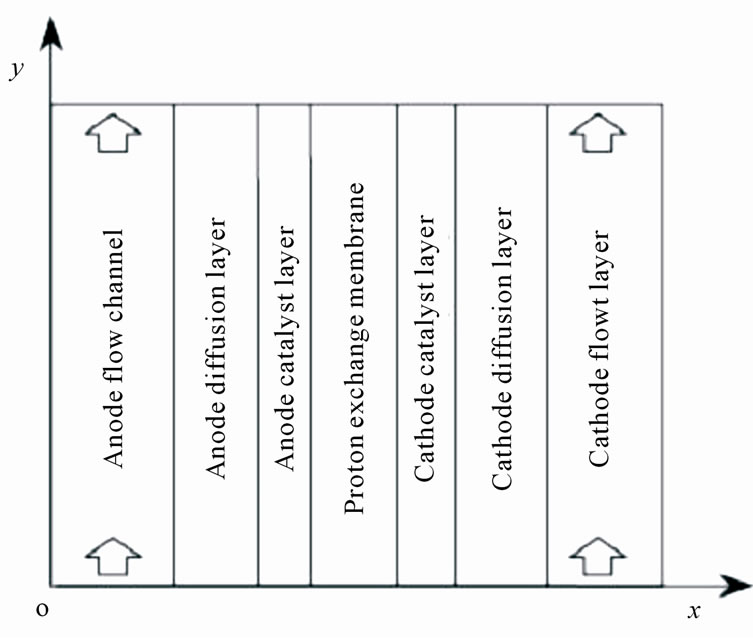
Figure 1. Coordinates of fuel cell for presented model.
7) Due to smaller depth of ethanol and water transporttation channel than its length, reactants concentration change along x direction inside the channel has been neglected.
8) Pressure drop inside channel is neglected.
9) Fluid flows at constant velocity inside the channels.
2. Basic Equations
Anode and cathode overall reaction is as follows
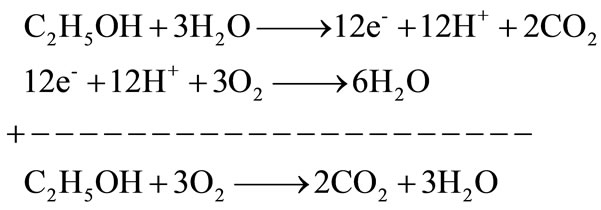 (1)
(1)
Ethanol concentration inside anodic channel, 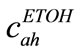 could be mentioned as below
could be mentioned as below
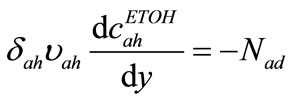 (2)
(2)
Whereas 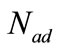 is mass flux from anodic channel through diffusion layer. Based on Fick’s law, we can write the following equation for mass flux, whereas
is mass flux from anodic channel through diffusion layer. Based on Fick’s law, we can write the following equation for mass flux, whereas  is diffusion coefficient of ethanol through diffusion layer
is diffusion coefficient of ethanol through diffusion layer
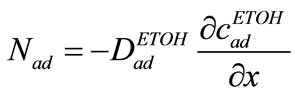 (3)
(3)
It can be noticed that for 12 M electron production, 1 M ethanol is consumed. Furthermore ethanol crossover lead to a part of ethanol permeate through membrane, so
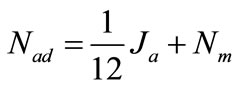 (4)
(4)
Current density can be written as below
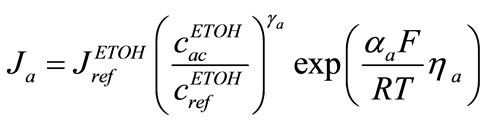 (5)
(5)
In which 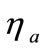 is anodic over potential and
is anodic over potential and 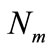 is crossover from membrane as below
is crossover from membrane as below
 (6)
(6)
The equations for cathode are similar to those for the anode, so
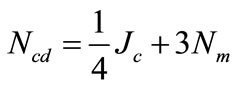 (7)
(7)
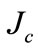 , current density is
, current density is
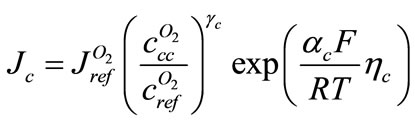 (8)
(8)
That 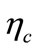 is cathodic over potential. Equations (2) and (3) can be written for cathode, thus
is cathodic over potential. Equations (2) and (3) can be written for cathode, thus
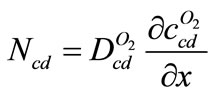 (9)
(9)
For oxygen concentration variation inside channel
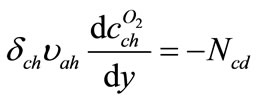 (10)
(10)
At last, for fuel cell voltage and current density, following equations is determined
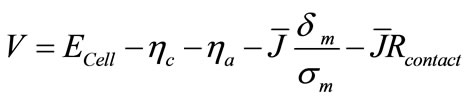 (11)
(11)
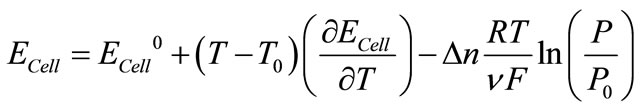 (12)
(12)
That ![]() is current density,
is current density, 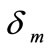 membrane thickness,
membrane thickness, 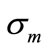 membrane conductivity,
membrane conductivity, 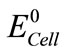 ideal electromotive force, and
ideal electromotive force, and 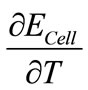 is electromotive difference rate.
is electromotive difference rate. 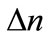 (Difference of exchanged gas moles between two sides of reaction in (1)) and
(Difference of exchanged gas moles between two sides of reaction in (1)) and ![]() (number of exchanged electrons) are constants which are –1 and 12 for (DEFC) respectively. Other symbols are listed in Table 1 or Nomenclature.
(number of exchanged electrons) are constants which are –1 and 12 for (DEFC) respectively. Other symbols are listed in Table 1 or Nomenclature.
3. Analytical Solution
In this solution, ethanol concentration in cathode layer in neglected (zero) and ethanol is linearly distributed, thus
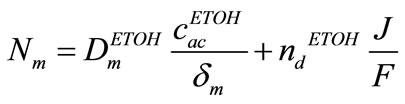 (13)
(13)
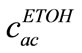 and
and ![]() are substituted with
are substituted with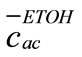 ,
, 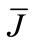 respectively, and then will be found
respectively, and then will be found
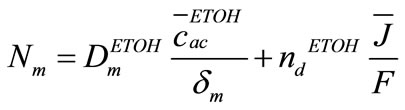 (14)
(14)
By substituting Equation (7) in Equation (9) and integrating from 0 to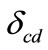 , oxygen concentration in catalyst layer is
, oxygen concentration in catalyst layer is
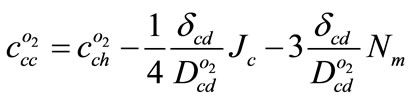 (15)
(15)
By assuming 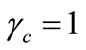 and substituting Equation (8) in Equation (15)
and substituting Equation (8) in Equation (15)
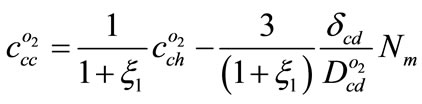 (16)
(16)
Whereas 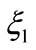 is defined as follows
is defined as follows

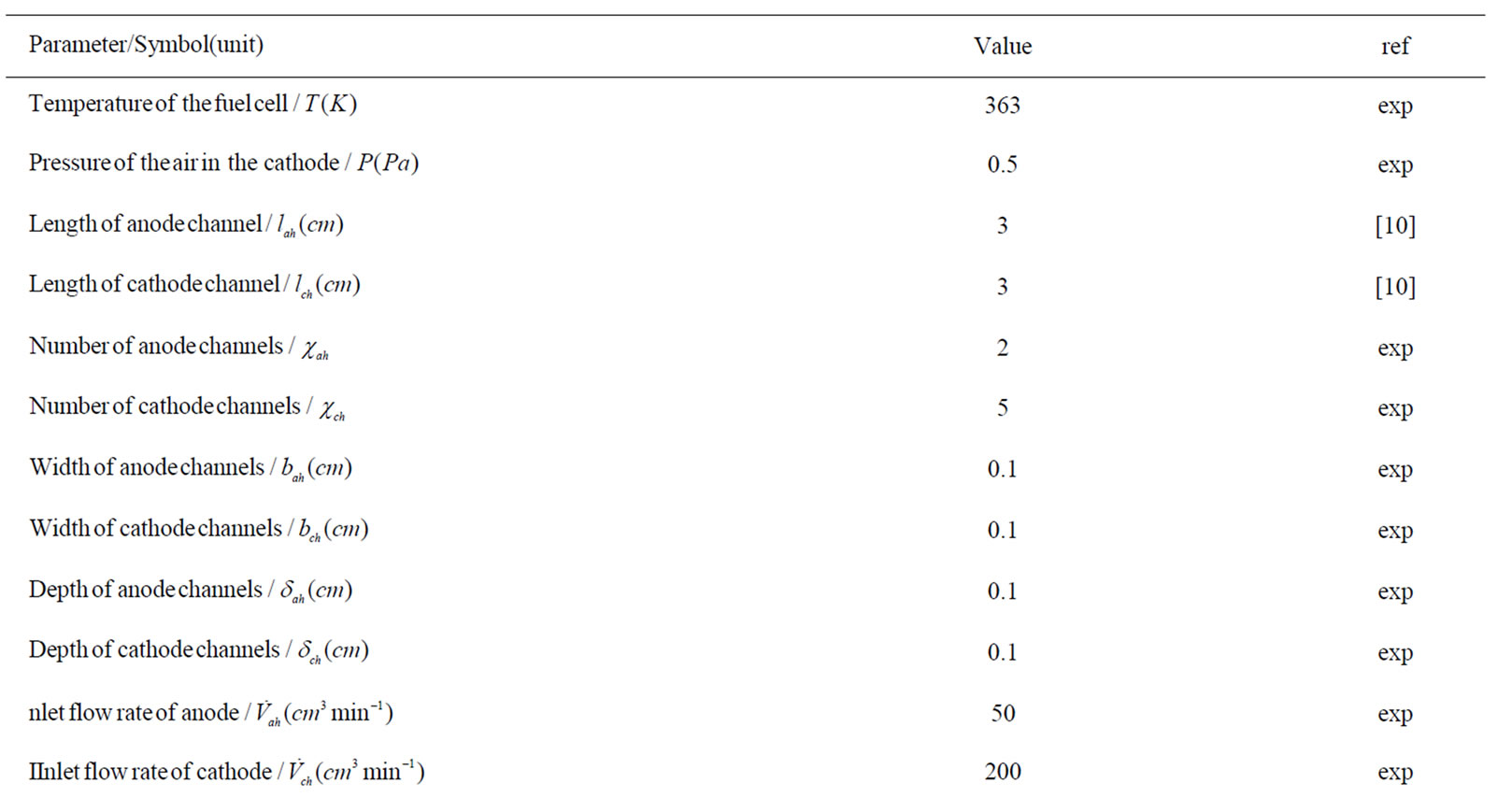
Table 1. Coefficients for analytical model.
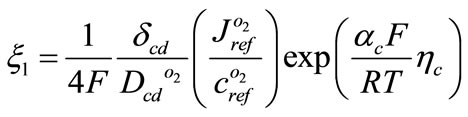 (17)
(17)
With regard to Equations (7), (8), (10) and (16) the below equation is acquired
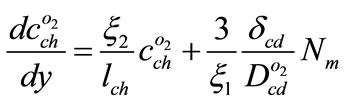 (18)
(18)
whereas 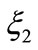 is
is
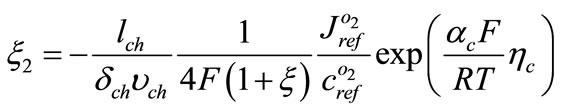 (19)
(19)
At last, by integrating Equation (18) and assuming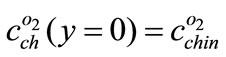 , oxygen concentration inside anode channel will be found
, oxygen concentration inside anode channel will be found
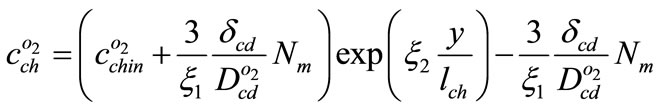 (20)
(20)
Concentration of oxygen in the catalyst layer can be determined by substituting (20) into (16)
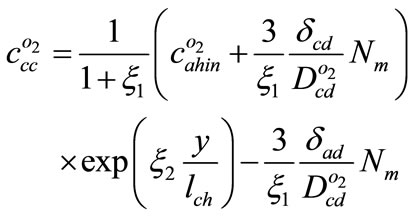 (21)
(21)
Substituting Equation (21) into (8) and integrating
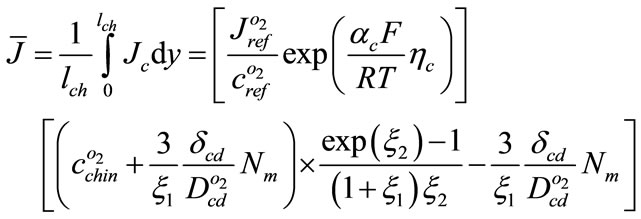 (22)
(22)
Such trend can be implemented for anode side, thus Ethanol concentration variation inside anode channel could be written as follows
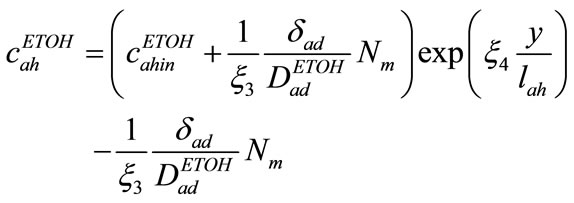 (23)
(23)
Ethanol concentration distribution in the catalyst layer is
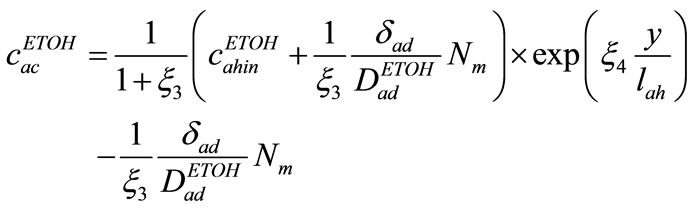 (24)
(24)
Ethanol concentration average in the catalyst layer, by integrating (24) through  to
to 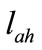 is
is
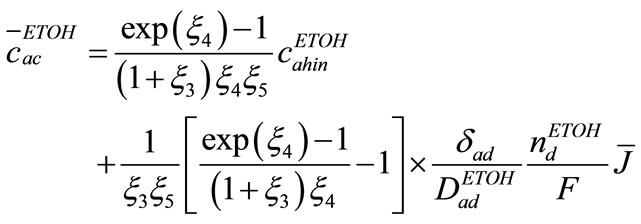 (25)
(25)
Average current density
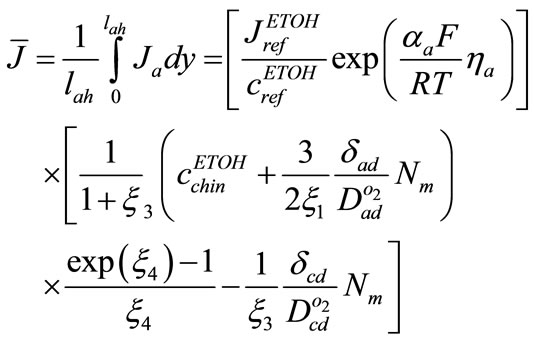 (26)
(26)
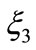 ,
, 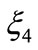 ,
, 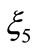 are variants as below
are variants as below
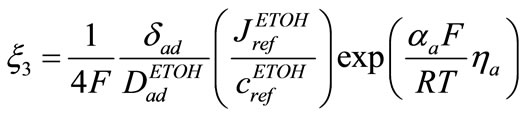 (27)
(27)
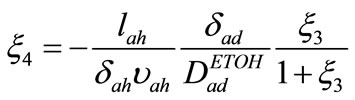 (28)
(28)
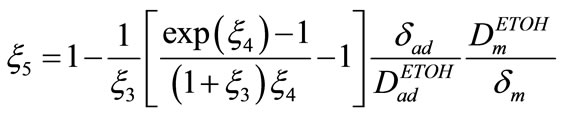 (29)
(29)
Finally, by using Equations (14), (25), and (26), following equations between anode over potential and cur rent density is attained
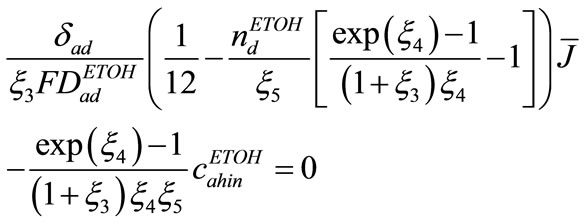 (30)
(30)
Using Equations (14), (22), (25), following equation between cathode over potential and current density could be presented
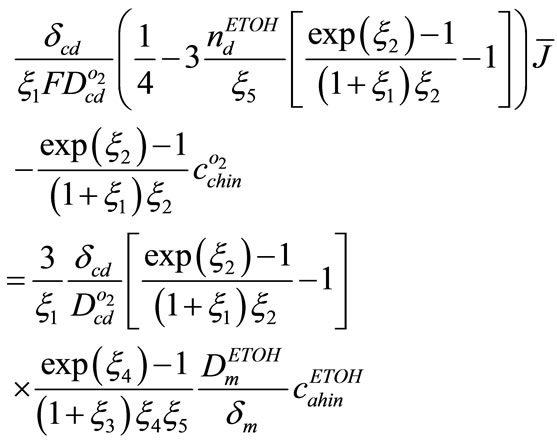 (31)
(31)
By using Equations (11) and (12) and combining them with Equations (30) and (31) polarization curves will be obtained. It should be mentioned that these two equations are solved by numerical methods
4. Results and Discussion
4.1. Comparison of Experimental and Analytical Results
After In this section analytical results will be compared with experiments. These experiments are performed under certain condition.
Pt/Ru/C catalyst was used for anode side and Pt/C black for cathode side. Catalyst loading on both sides was 4 mg/cm2. and Nafion 117 was used as membrane and flow channel wide and depth was 1mm. Cathode and anode flow channel pattern was 5 parallel and 2 parallel serpentine respectively. The cell was humidified by hot water for 2hours and activated by 1 M ethanol. Active area was 10 × 10 cm2 and back plates were made of aluminum.
For checking analytical model, because of some undefined coefficients, (assumed parameters in Table 1) first 0.125 M analytical curve is fitted to experimental curve then for other molarities analytical and experimental results will be compared (Figures 2-5). The results of comparison showed that at the first and second region of polarization curve, (Activation loss and Ohmic loss regions [18]) model predicts fuel cell performance well, but in the third zone (concentration loss region [18]) it seems that because of concentration loss negligence, and increase of molarity analytical somewhat model lost its accuracy.
Coefficients of analytical model are gathered in Table 1.
4.2. Ethanol Concentration Distribution Inside the Channel and over Potential Variation
Equation (23) foretells ethanol concentration variation inside anode channel exponentially, but based on Figure 6 ethanol concentration inside anodic channel can be considered almost linearly.
Over potential variation both for anode and for cath-
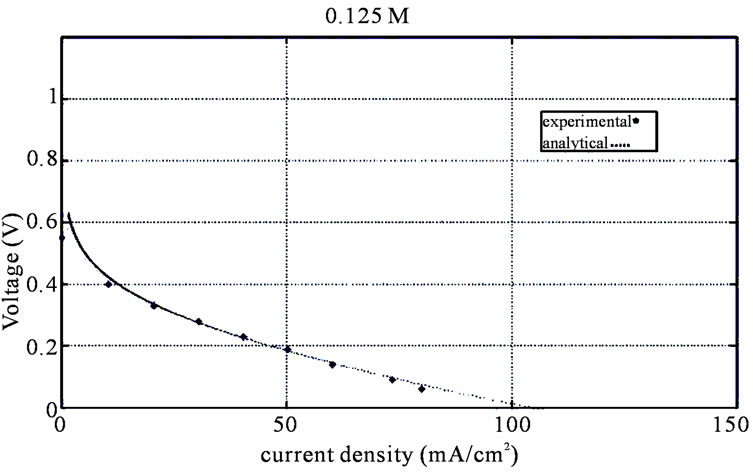
Figure 2. Comparison of experimental and analytical polarization curves for 0.125 M.
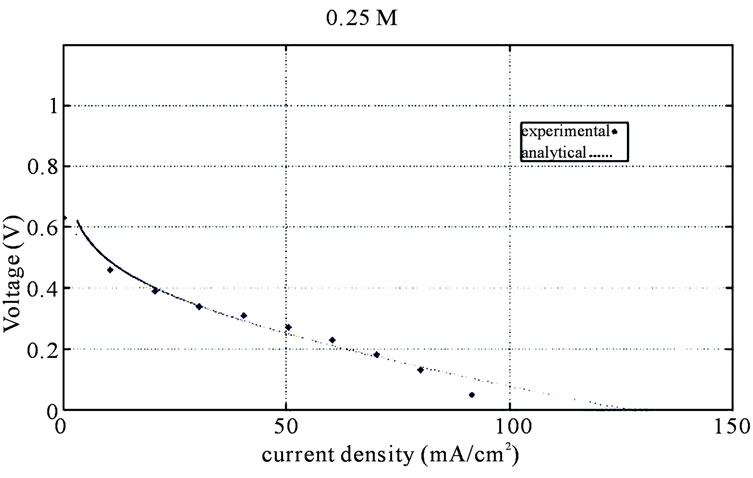
Figure 3. Comparison of experimental and analytical polarization curves for 0.25 M.
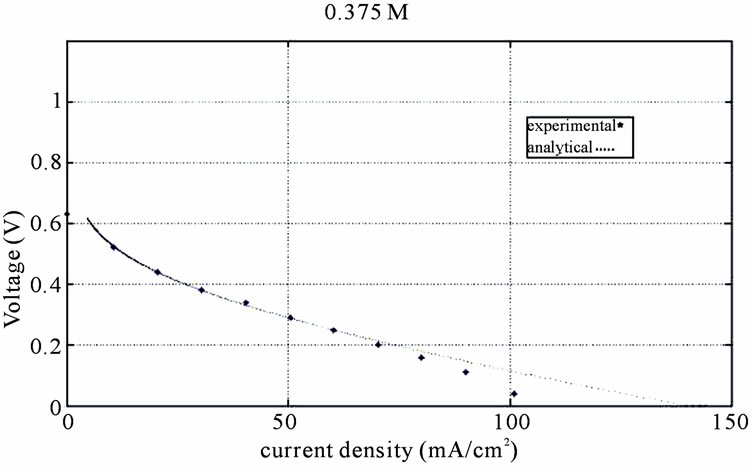
Figure 4. Comparison of experimental and analytical polarization curves for 0.375 M.
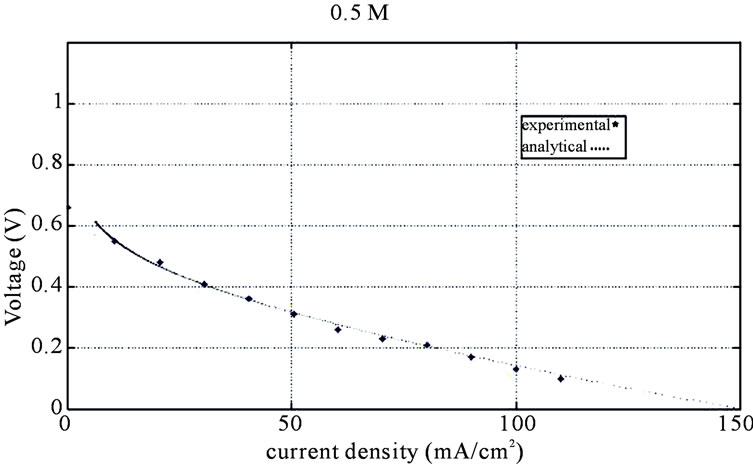
Figure 5. Comparison of experimental and analytical polarization curves for 0.5 M.
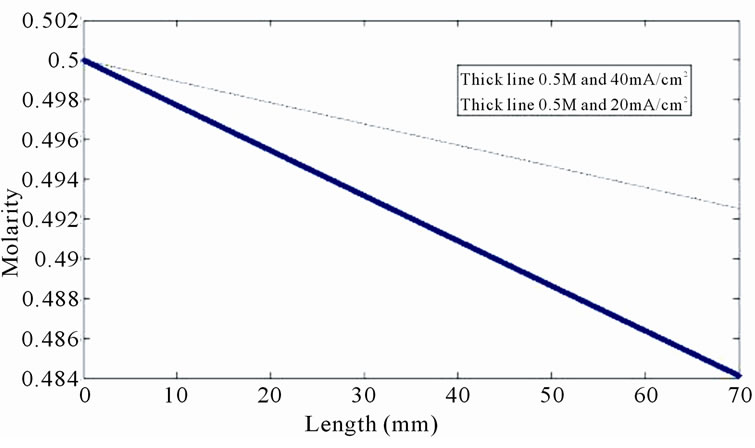
Figure 6. Ethanol concentration distribution inside anodic channel for 0.5 M; thick line 40 mA/cm2 and thin line 20 mA/cm2.
ode can be estimated Based on proposed analytical model. With regard to attained curve for anode over potential versus current density, by increasing current density, anodic over potential will increase, but for cathodic over potential, by increasing current density, cathodic over potential will remain approximately zero (Figures 7 and 8). These results are both for 0.5 M and for 0.25 M and match cathodic over potential results of G. Andreadis.
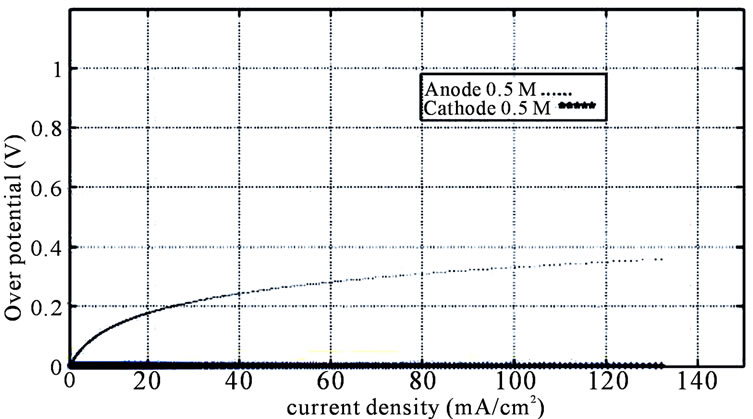
Figure 7. Anodic and cathodic over potential variation versus current density for 0.25 M.
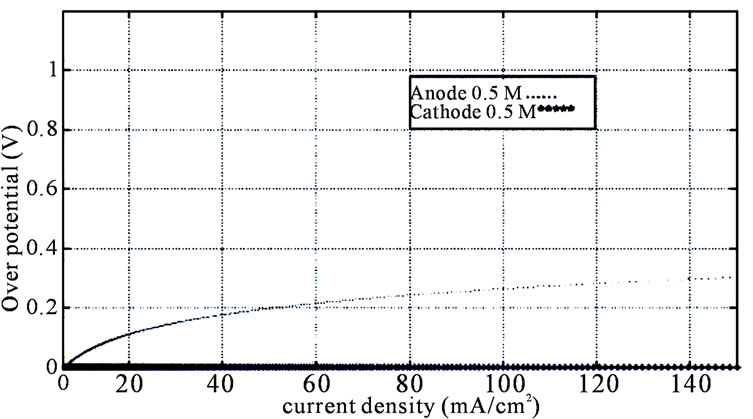
Figure 8. Anodic and cathodic over potential variation versus current density for 0.5 M.
5. Conclusions
In this paper by an analytical 2D model, (DEFC) performance was predicted. This model is capable of estimating polarization curves up to 0.5 M. This model is precise in the first and second zone (Activation and Ohmic loss region), but in the third zone (Concentration loss region) because of neglecting concentration loss and increasing inlet ethanol concentration, model error will increase and it will have more difference with experimental curves. Based on model, ethanol concentration varies almost linearly inside anodic channel. By increasing current density cathodic over potential remains zero but anodic over potential will increase up to certain value.
REFERENCES
- T. Pichonat and B. Gauthier-Manuel, “Recent Developments in MEMS-Based Miniature Fuel Cells,” Microsyst Technol, Vol. 13, No. 11-12, 2007, pp. 1671-1678. doi:10.1007/s00542-006-0342-5
- A. Casalegno and R. Marchesi, “DMFC Performance and Methanol Cross-Over: Experimental Analysis and Model Validation,” Journal of Power Source, Vol. 185, No. 1, 2008, pp. 318-330. doi:1016/j.jpowsour.2008.06.071
- N. Fujiwara, Sh. Yamazaki, Z. Siroma, T. Ioroi and K. Yasuda, “L-Ascorbic Acid as an Alternative Fuel for Direct Oxidation Fuel Cells,” Journal of Power Sources, Vol. 167, No. 1, 2007, pp. 32-38. doi:10.1016/j.jpowsour.2007.02.023
- N. Fujiwara, Z. Siroma, Sh. Yamazaki, T. Ioroi, H. Senoh and K. Yasuda, “Direct Ethanol Fuel Cells Using an Anion Exchange Membrane,” Journal of Power Sources. Vol. 185, No. 2, 2008, pp. 621-626. doi:10.1016/j.jpowsour.2008.09.024
- Sh. Song and P. Tsiakarasc, “Recent Progress in Direct Ethanol Proton Exchange Membrane Fuel Cells (DEPEMFCs),” Applied Catalysis B: Environmental, Vol. 63, No. 3-4, 2006. pp. 187-193. doi:10.1016/j.apcatb.2005.09.018
- E. Antolini, “Catalysts for Direct Ethanol Fuel Cells,” Journal of Power Sources, Vol. 170, No. 1, 2007, pp. 1-12. doi:10.1016/j.jpowsour.2007.04.009
- E. H. Hou, G. Suna, R. Heb, Zh. Wu and B. Sunb, “Alkali Doped Polybenzimidazole Membrane for High Performance Alkaline Direct Ethanol Fuel Cell,” International Journal of Hydrogen Energy, Vol. 33, No. 1, 2008, pp. 7172-7176. doi:10.1016/j.jpowsour.2008.04.010
- G. M. Andreadis, A. K. M. Podias and P. E. Tsiakaras, “The Effect of the Parasitic Current on the Direct Ethanol PEM Fuel Cell Operation,” Journal of Power Sources Vol. 181, No. 2, 2008, pp. 214-227. doi:10.1016/j.jpowsour.2008.01.060
- W. J. Zhou, S. Q. Song, W. Z. Li, Z. H. Zhou, G. Q. Sun, Q. Xin, S. Douvartzides and P. Tsiakaras, “Direct Ethanol Fuel Cells Based on Pt/Sn Anodes: The Effect of Sn Content on the Fuel Cell Performance,” Journal of Power Source, Vol. 140, No. 1, 2005, pp. 50-58. doi:10.1016/j.jpowsour.2004.08.003
- K. Scott, W. M. Taama, S. Kramer, P. Argyropoulos and K. Sundmacher, “Limiting Current Behaviour of the Direct Methanol Fuel Cell,” Electrochimica Acta, Vol. 45, No. 6, 1999, pp. 945-957. doi:10.1016/S0013-4686(99)00285-6
- K. Scott, W. Taama and J. Cruickshank, “Performance and Modelling of a Direct Methanol Solid Polymer Electrolyte Fuel Cell,” Journal of Power Sources, Vol. 65, No. 1-2, 1997, pp.159-171. doi:10.1016/S0378-7753(97)02485-3
- S. Kato, K. Nagahama and H. Asai, “Permeation Rates of Aqueous Alcohol Solutions in Pervaporation through Nafion Membranes,” Journal of Membrance Science, Vol. 72, No. 1, 1992, pp. 31-41. doi:10.1016/0376-7388(92)80054-N
- G. Andreadis and P. Tsiakaras, “Ethanol Crossover and Direct Ethanol PEM Fuel Cell Performance Modeling and Experimental Validation,” Chemical Engineering Science, Vol. 61, No. 22, 2006, pp. 7497-7508. doi:10.1016/j.ces.2006.08.028
- G. Andreadis, S. Song and P. Tsiakaras, “Direct Ethanol Fuel Cell Anode Simulation Model,” Journal of Power Sources, Vol. 157, No. 2-3, 2006, pp. 657-665. doi:10.1016/j.jpowsour.2005.12.040
- F. Vigier, C. Coutanceau, A. Perrard, E. M. Belgsir and C. Lamy, “Developments of Anode Catalysts for a Direct Ethanol Fuel Cell,” Journal of Applied Electrochemistry, Vol. 34, No. 4, 2004, pp. 439-446. doi:10.1023/B:JACH.0000016629.98535.ad
- X. Ren, W. Henderson and S. Gottesfeld, “Electro-Osmotic Drag of Water in Ionomeric Membranes,” Jouranl of Electrochemical Science, Vol. 144, No. 9, 1997, pp. L267- L270. doi:10.1149/1.1837940
- Z. H. Wang and C. Y. Wang, “Mathematical Modeling of Liquid-Feed Direct Methanol Fuel Cells,” Journal of Electrochemical Socience, Vol. 150, No. 4, 2003, pp. A508- A519. doi:10.1149/1.1559061
- R. O’Hayre, S. Cha, Wh. Colella and F. B. Prinz, “Fuel Cell Fundamentals,” Wiley, New York, 2005.
Nomenclature
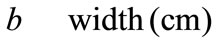

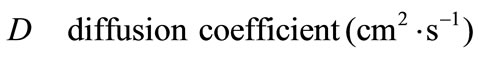
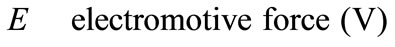
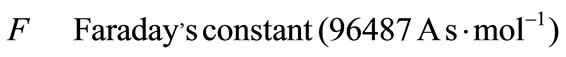
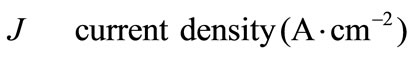
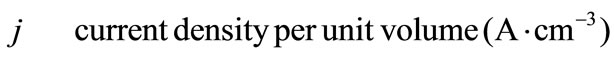
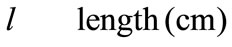

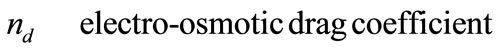

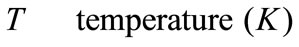
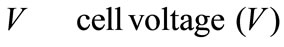
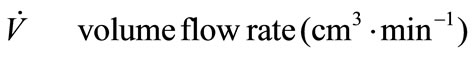
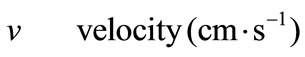

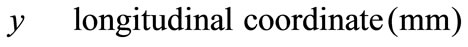
Greek Symble
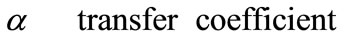
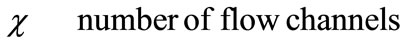
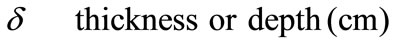
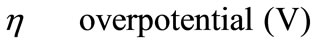
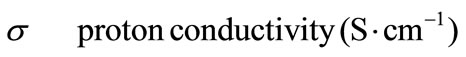
Superscript
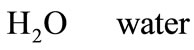
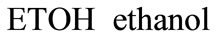
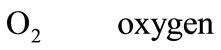
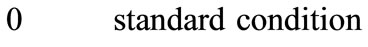
Subscript