ABSTRACT

Let be a fixed pythagorean angle. We study the abelian group 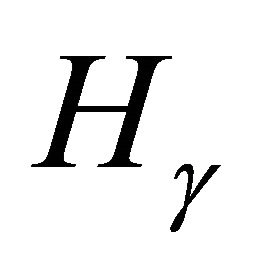of primitive integral triangles 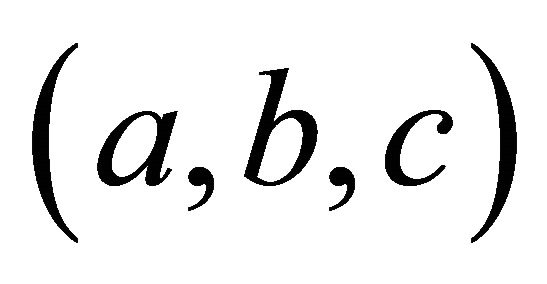for which the angle opposite side c is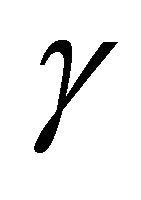. Addition in 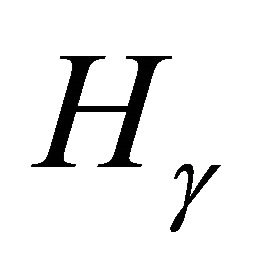is defined by adding the angles opposite side b and modding out by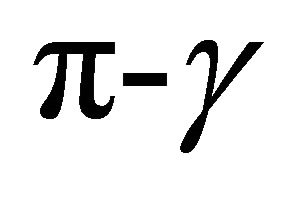. The only 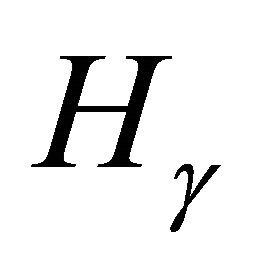for which the structure is known is, which is free abelian. We prove that for general, has an element of order two iff 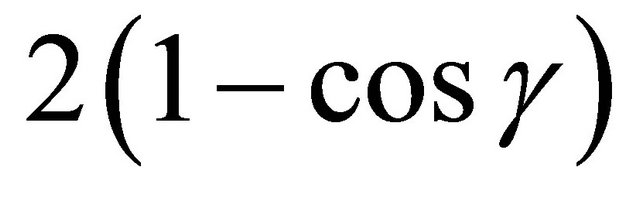is a rational square, and it has elements of order three iff the cubic 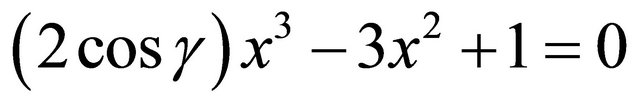has a rational solution. This shows that the set of values of 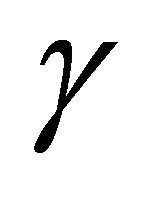for which 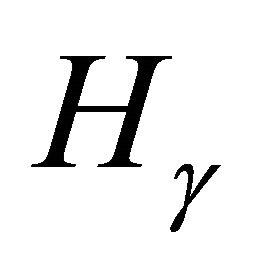has two-torsion is dense in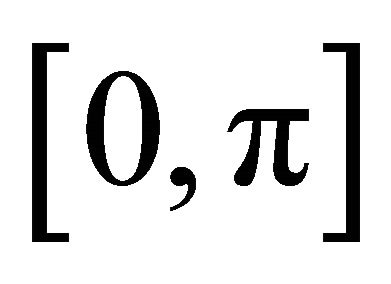, and similarly for three-torsion. We also show that there is at most one copy of either 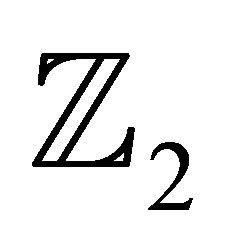or in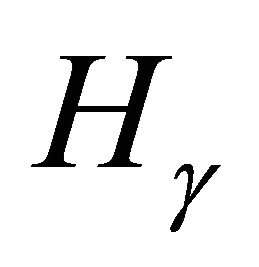. Finally, we give some examples of higher order torsion elements in.

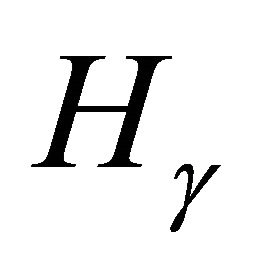1. Introduction

In [1], Olga Taussky introduces a group operation on the set of primitive pythagorean triples

that is, the set of primitive integral triangles 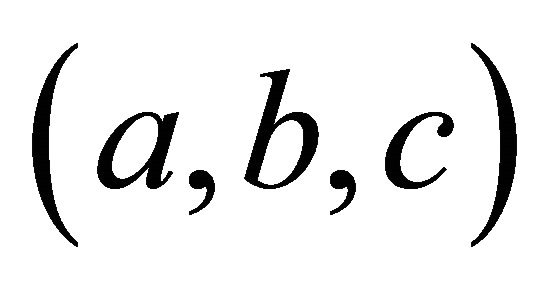in which the angle 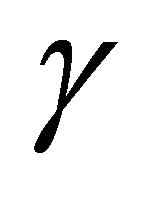opposite side c is a right angle. Ernest J. Eckert spells out the details of the group operation in [2]:

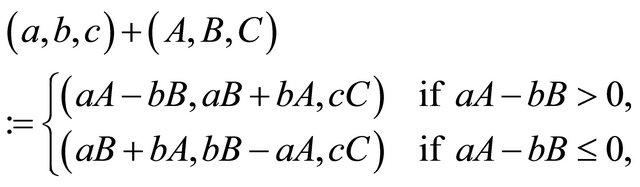
where we reduce the answer by a common factor if necessary to obtain a primitive triple. The group has identity; the inverse of is.

The construction arises from the famous identity on sums of squares:

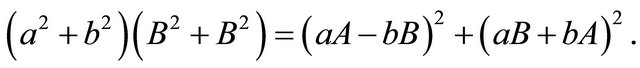
This identity, of course, corresponds to the rule 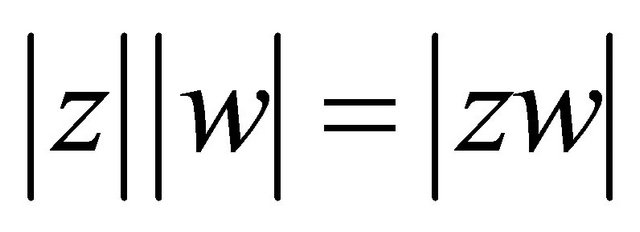for complex numbers, and the group law on pythagorean triples has a similar geometric motivation: we identify the triangle with the complex number, and the group operation is then just complex multiplication.

The argument of 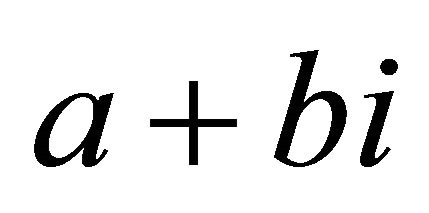is the angle opposite side b of the triangle. Since we add the arguments of complex numbers when we multiply the numbers, we can interpret the group operation as addition of the angles and 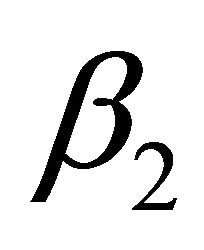to find a primitive triple whose corresponding angle is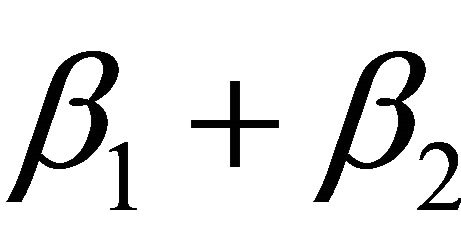. A problem arises when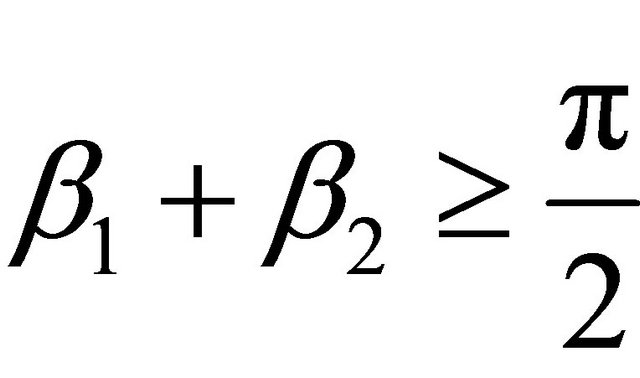i.e. when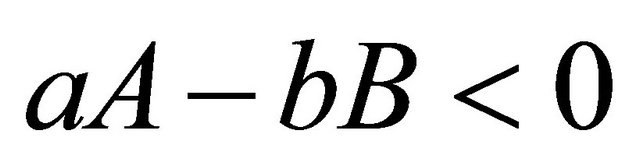, since this no longer corresponds to a pythagorean triple with positive coordinates. To fix this, we mod out the angle by; this is why we have the two cases in the definition of the group operation above.

This group has been the subject of much interest over the years. In [3], Jean Mariani studies the group of homogeneous linear transformations with integral coefficients that preserve the triangles above as a set. In [4], Barbara Margolius uses a sequence of pythagorean triples derived from the group law above to prove that Plouffe’s constant is transcendental, a special case of Hilbert’s seventh problem.

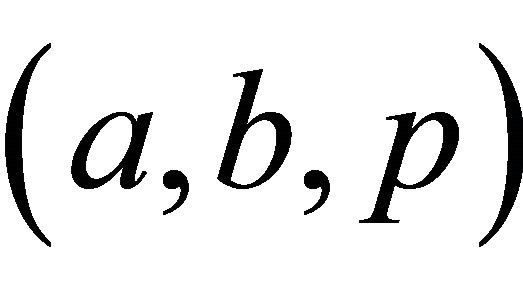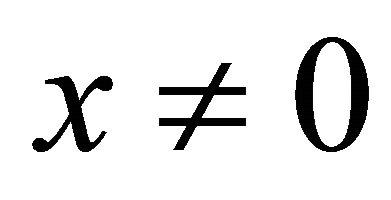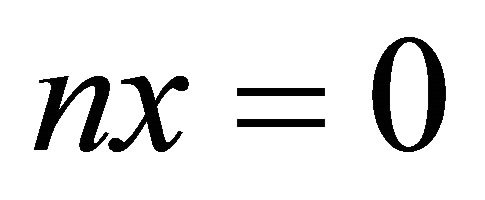Eckert’s main result in [2] is that this group is free abelian, that is, isomorphic to a direct sum of copies of the integers. The sum is indexed by the triangles, where and p is prime with. In particular, the group is torsion-free, that is, there do not exist any nontrivial elements with for.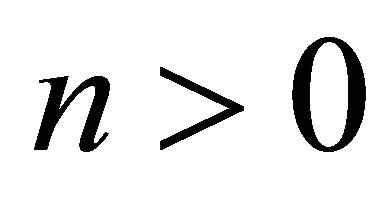

In [5], Eckert and Preben Dahl Vestergaard generalize the construction above to the case when 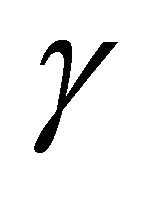is no longer a right angle. We define an angle to be pythagorean if or 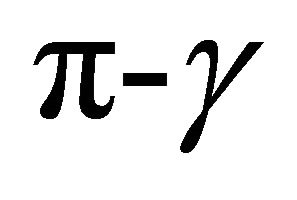is an angle in a pythagorean triangle, or, equivalently, if and are both rational. For a fixed pythagorean angle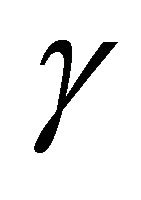, we define 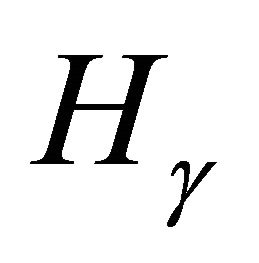to be the set of primitive integral triangles 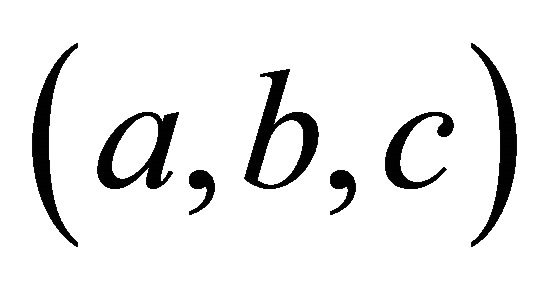for which the angle opposite side c is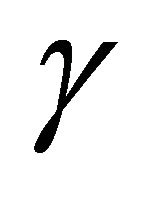. We can add two triangles by adding their values for, modulo: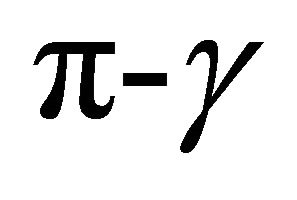

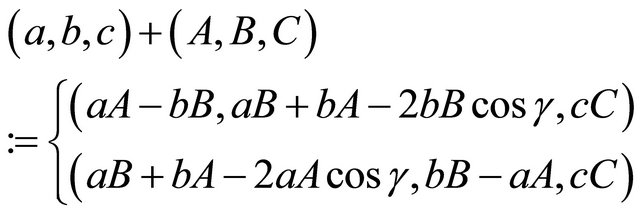
We use the first formula above in the case when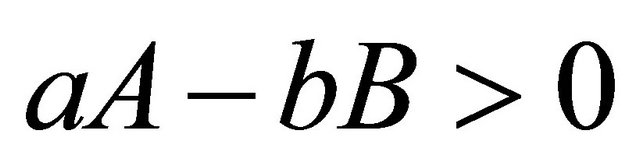, which corresponds to, and the second when, which corresponds to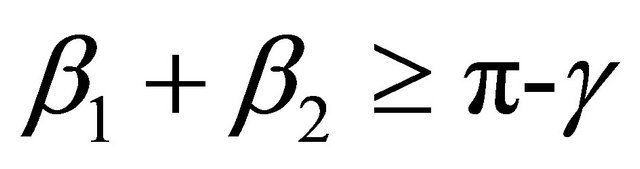. As before, we stipulate that we will scale the answer by a common factor if necessary to obtain a primitive integral triangle. Eckert and Vestergaard prove that this construction again gives us a group, still with identity 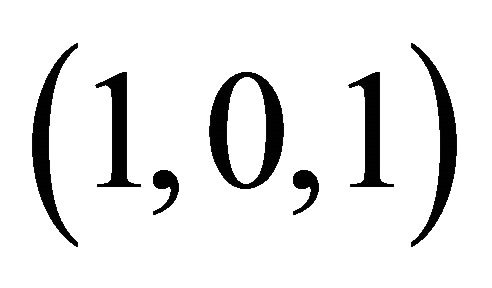and with the inverse of 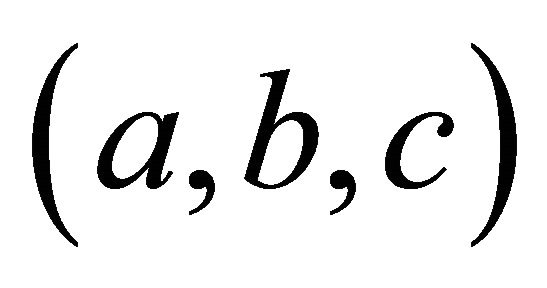being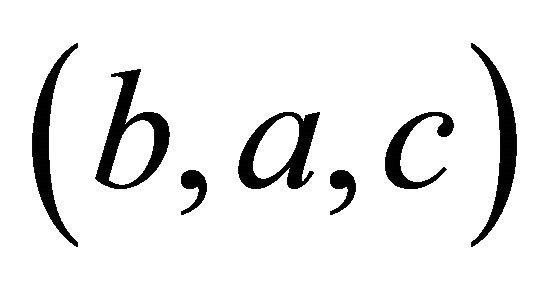. Note that the original group considered in [2] is just the special case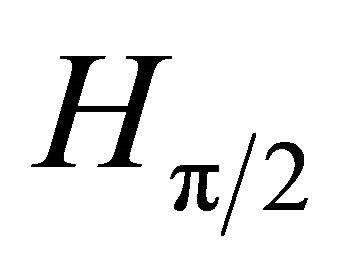, whose structure we know completely.

Eckert and Vestergaard ask a number of interesting questions about the structure of in general. They mention that when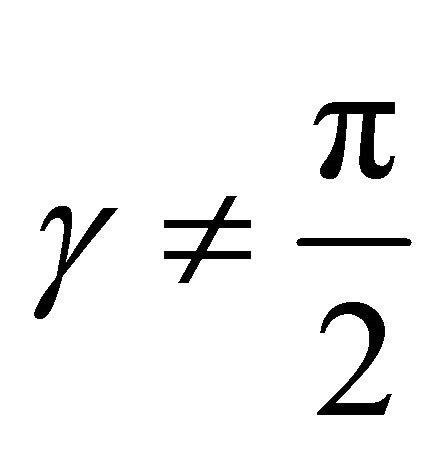, 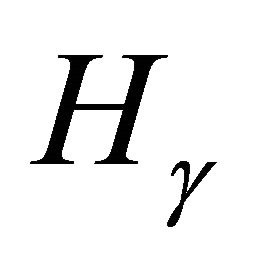can have nontrivial torsion elements, that is, elements 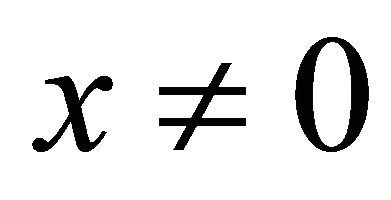such that 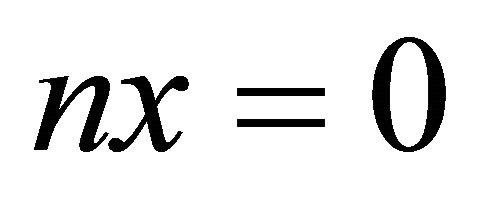for some, but they do not give details. In this paper, we pursue the study of torsion elements in. Our main results give necessary and sufficient conditions on for to have two-torsion and threetorsion. From these theorems, it will be easy to see that the set of values of for which 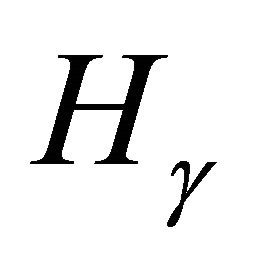has two-torsion is dense in the interval, and similarly for threetorsion. 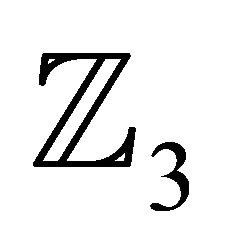We will also show that there is at most one copy of either or in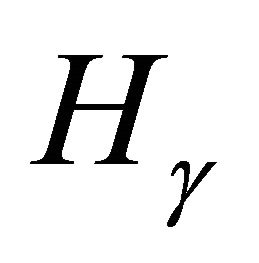. Finally, we will give some examples of higher-order torsion elements in.

2. Two-Torsion

Our results on two-torsion and three-torsion are similar in flavor, but the theorem on two-torsion is simpler and significantly easier to prove, so we will start there.

Theorem 1. 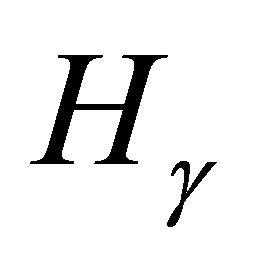has a point of order two iff is a rational square. When this is true, the point of order two is unique.

Proof of Theorem 1. Since the inverse of 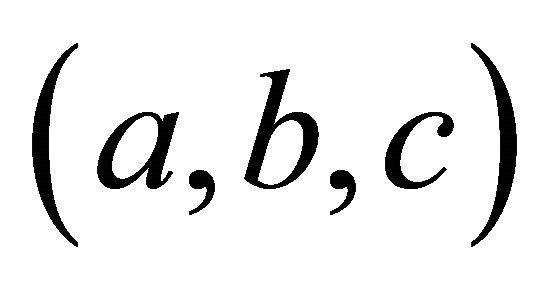is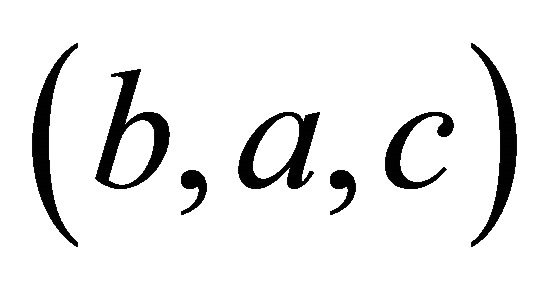, a point has order two iff it has the form.

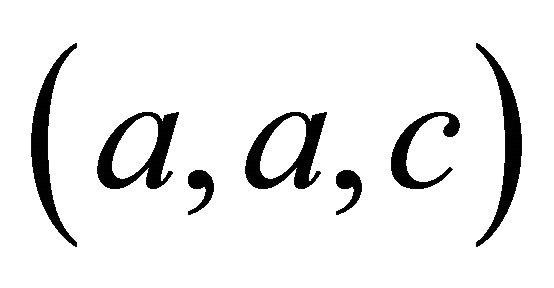Suppose first that is a point of order two. We invoke the Law of Cosines:

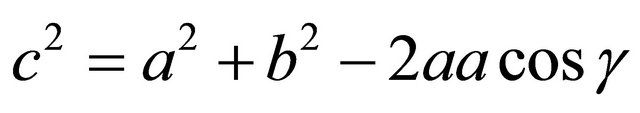
So 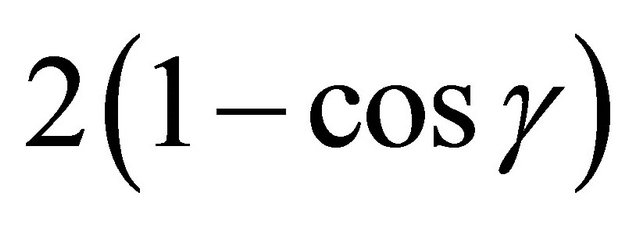is a rational square, as desired.

Conversely, suppose that, where a,

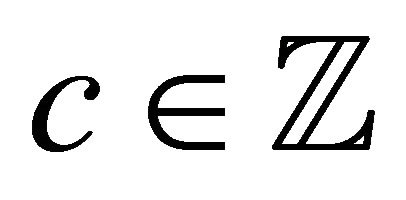are relatively prime. Note that 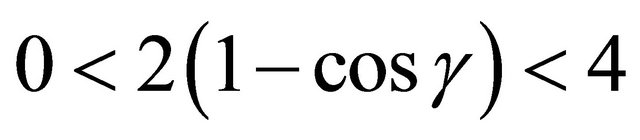, so, so 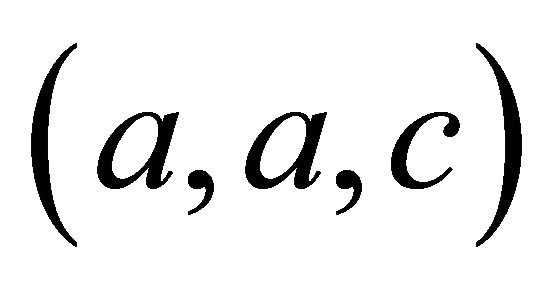is a triangle, and the computation above shows that by the Law of Cosines, the angle opposite side c is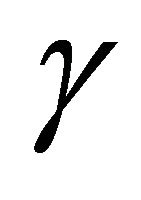. Hence is a point of order two.

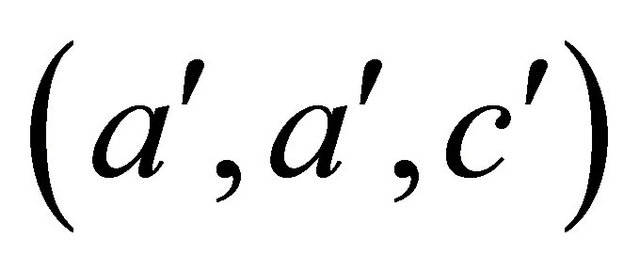To show that only one point of order two can exist, we note that any two triangles and in 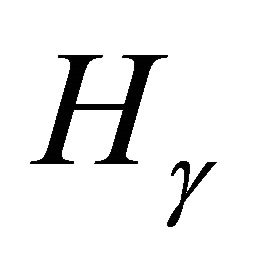would have to be scalar multiples of each other, and would therefore be represented by a single primitive integral triangle. ∎

We illustrate Theorem 1 with some quick examples:

1) For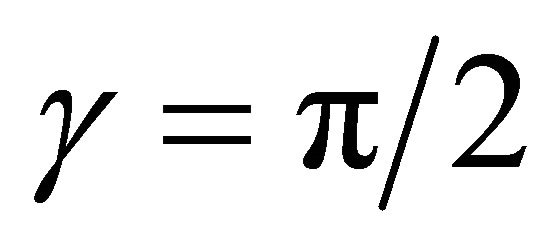, we have, and as shown in [2], has no point of order two.

2) For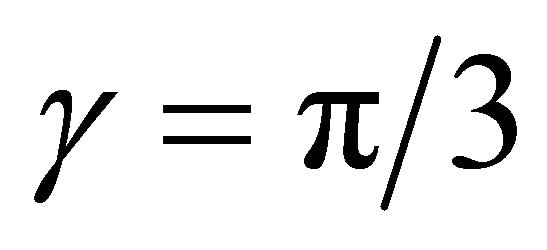, we have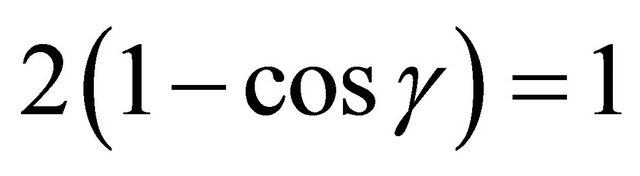, and 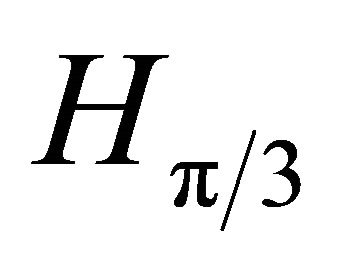contains the point (1, 1, 1) of order two.

3) For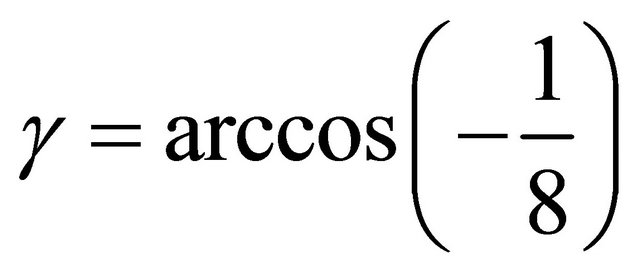, we have, and contains the point (2, 2, 3) of order two.

Corollary 2. The set of 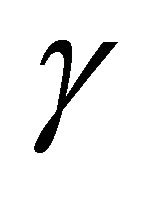for which contains a point of order two is dense in.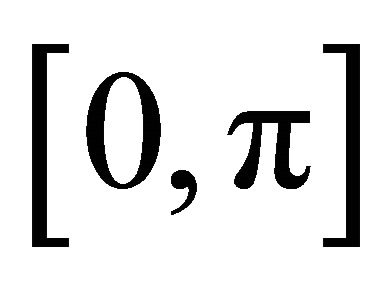

Proof. This follows from the fact that 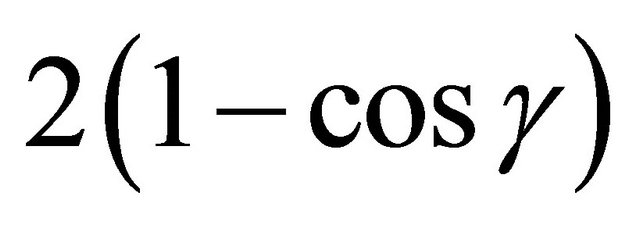is a continuous function from onto 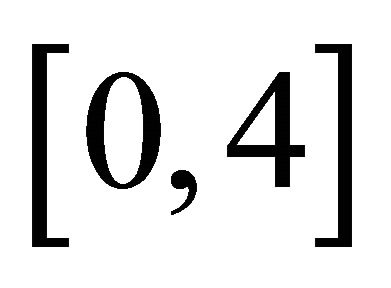and the rational squares are dense in. ∎

3. Three-Torsion

Our result for three-torsion follows the same general spirit as that for two-torsion, but is significantly harder. We first prove the easy result that 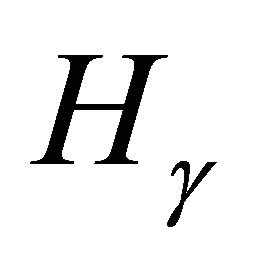contains at most one copy of; this proof will help set the stage for the proof of our main theorem.

Theorem 3. contains at most two points of order three.

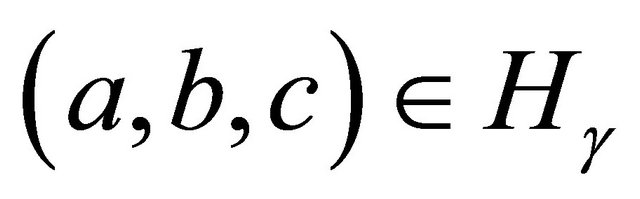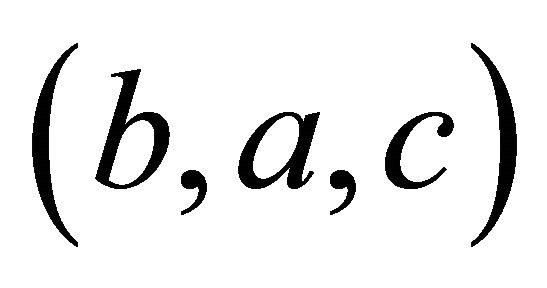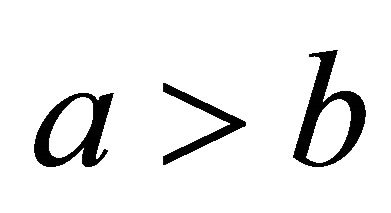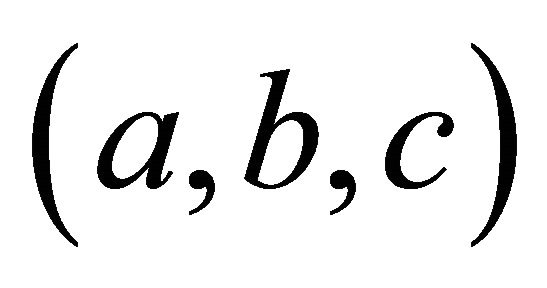Proof of Theorem 3: Suppose has order three. Note that its inverse also has order three, so we may assume without loss of generality that. (If, then as we saw above, has order two, so it cannot have order three). Let 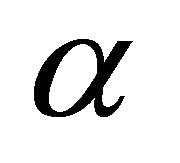and be the angles opposite sides a and b respectively. Since, we have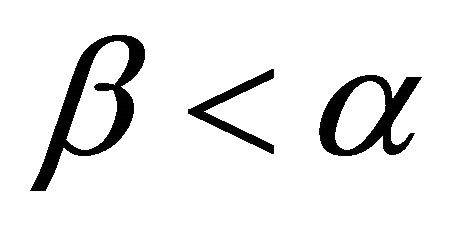, so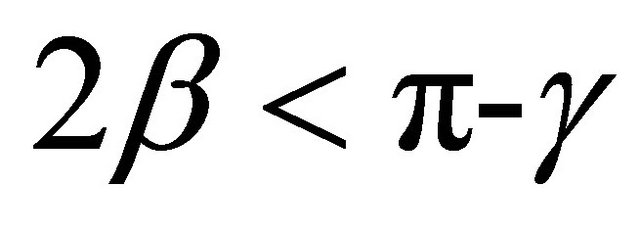. Thus, when we compute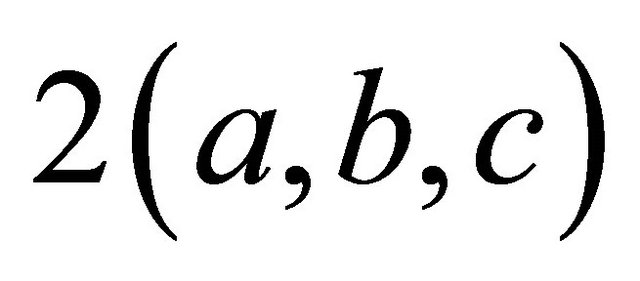, we are adding to itself, and there is no modding out by. The resulting triangle is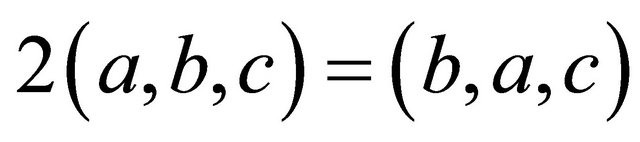, which has angle opposite side a, so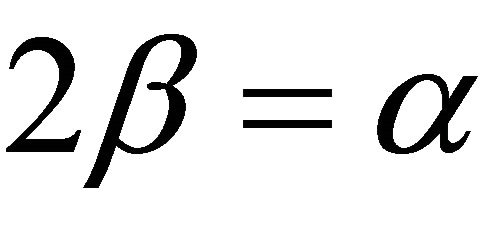. But since is fixed, the equation 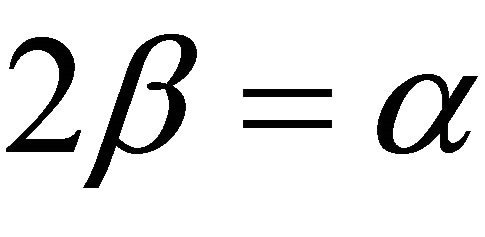completely determines the three angles of the triangle, so there is only one primitive triple with these angles. (The other point of order three, of course, is the inverse). ∎

We will continue to use some of the ideas above in the proof of our main theorem on three-torsion.

Theorem 4. 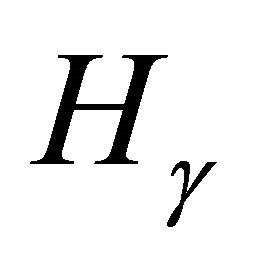has a point of order three iff the cubic

has a rational solution.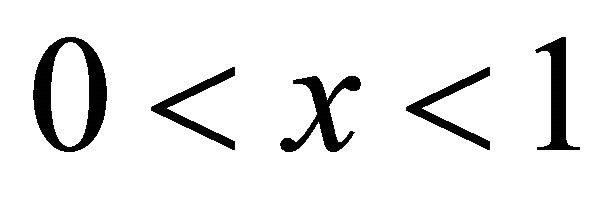

The cubic criterion gives easy answers to two questions: First, given a specified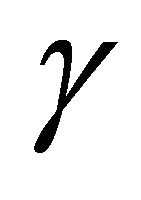, we can ask whether 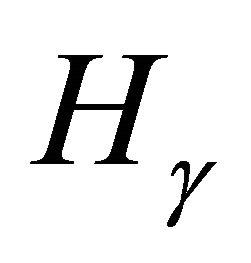has three-torsion. Assuming that 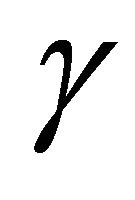is pythagorean, we can use the Rational Root Theorem to check quickly whether the cubic above has a rational solution between 0 and 1. If it does, the proof below will give a constructive algorithm to produce a triangle of order three.

Second, if we don’t have a specific 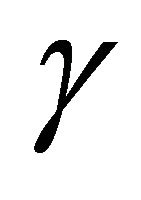in mind, we can use the cubic criterion to find values of for which has three-torsion. Indeed, we can solve the equation above for:

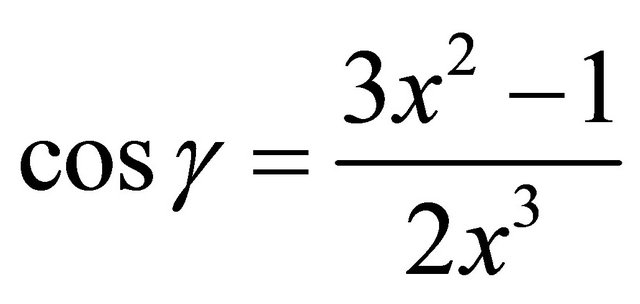
The rational function on the right takes values less than −1 for 0 < x < 1/2, and it maps the interval 1/2 ≤ x ≤ 1 continuously onto the range. Therefore, to find angles whose groups have three-torsion, we can take any rational 1/2 ≤ x ≤ 1 and then find the corresponding.

Proof of Theorem 4. First, suppose that 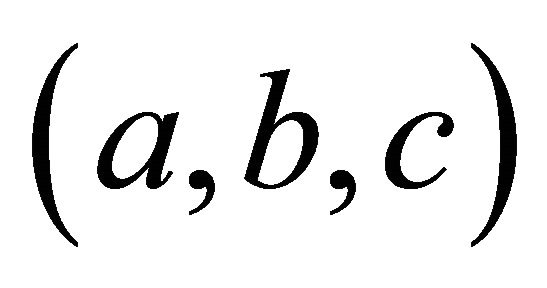has order three. As in the proof of Theorem 3 above, we may assume that a > b and that when we compute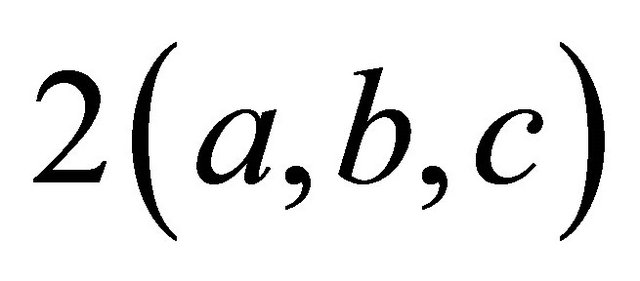, there is no modding out by. So we use the first set of equations for the group operation:

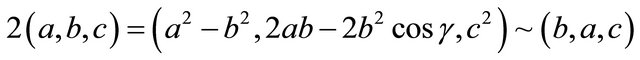
The common factor between the two triangles on the right is c, giving us the following “scaling equations”:

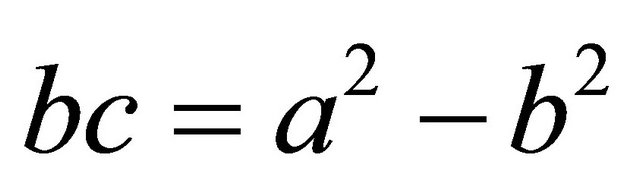
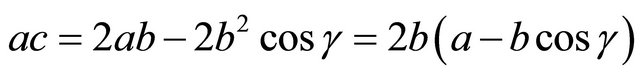
Solve the second scaling equation for c:

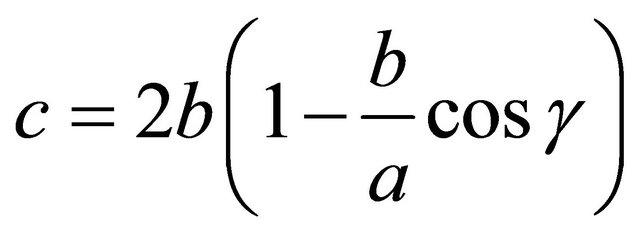
Plug this into the Law of Cosines:

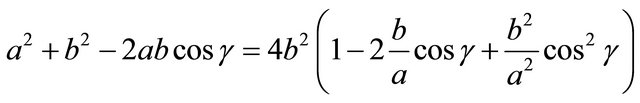
Multiply by:

Rearrange:

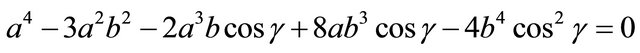
Factor:

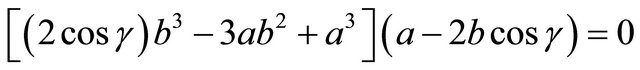
We claim that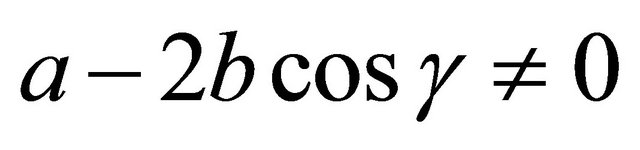. To prove this claimsuppose that; then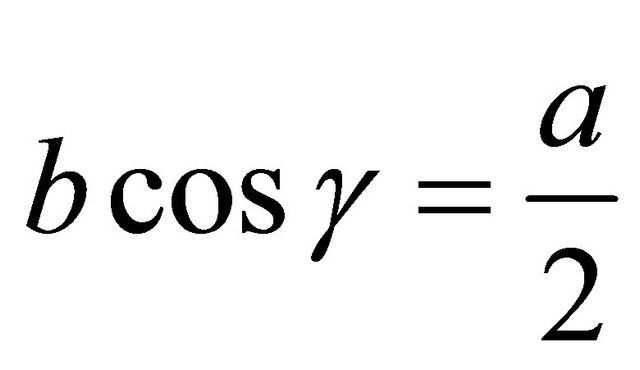. Plugging this into the second scaling equation, we get ac = ab, so b = c. Plugging this into the first scaling equation, we get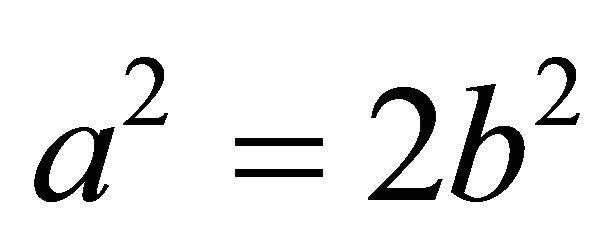, contradicting the fact that a and b are both integers. This proves our claim, so we may cancel the factor of:

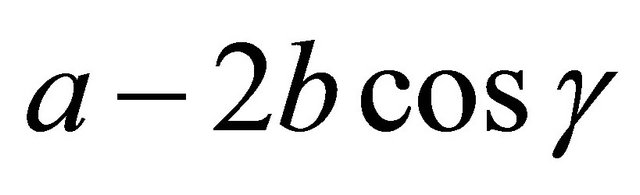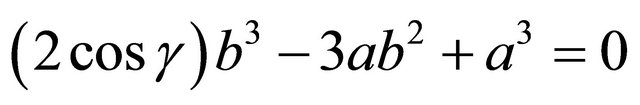
Divide by

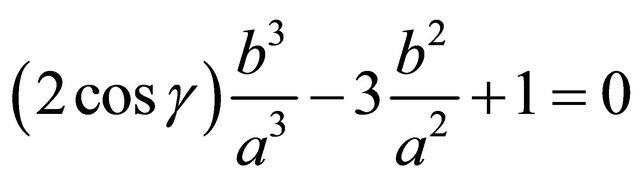
Set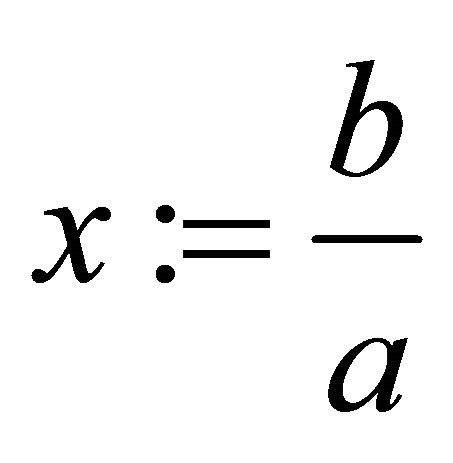, which is a rational number with 0 < x < 1, and we have

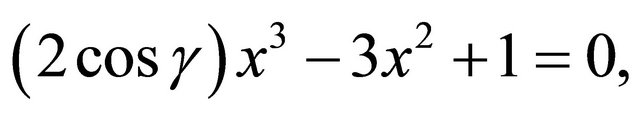
as desired.

Conversely, suppose we have a rational solution 0 < x < 1 to

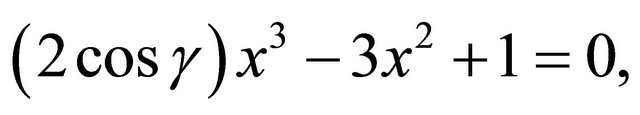
Define 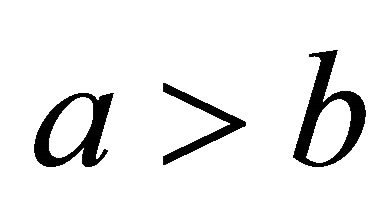to be positive relatively prime integers such that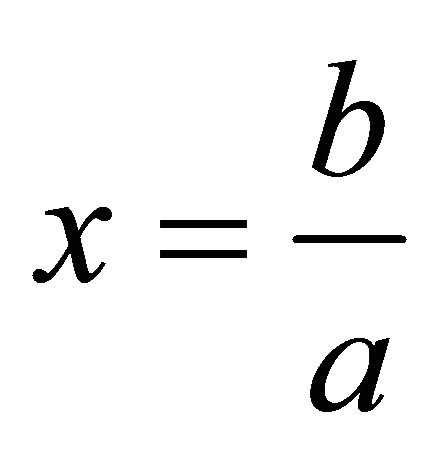, and define c to satisfy

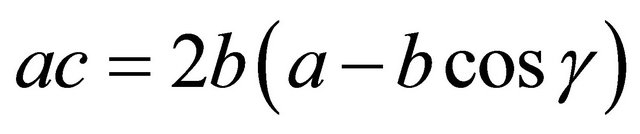. (Note that c > 0). Scale a, b, and c by a common factor, if necessary, to be relatively prime integers; note that this scaling will preserve both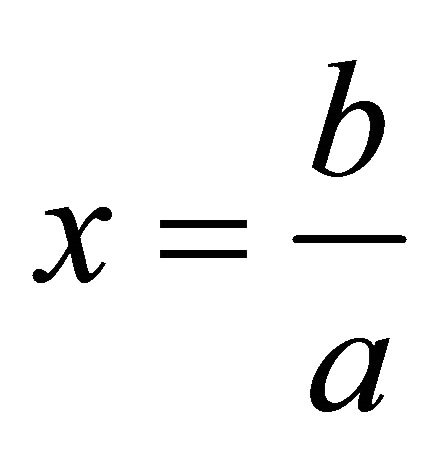

and.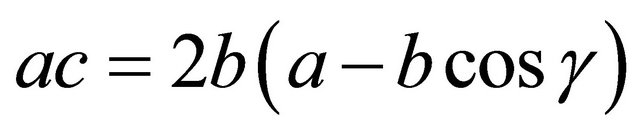

By reversing the equations from the forward direction of the proof, we can work back to

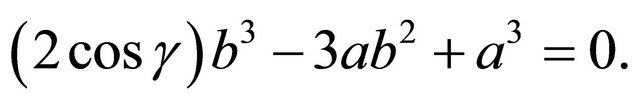
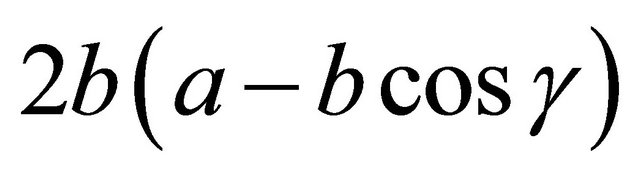We can solve this for and then build up to as follows:

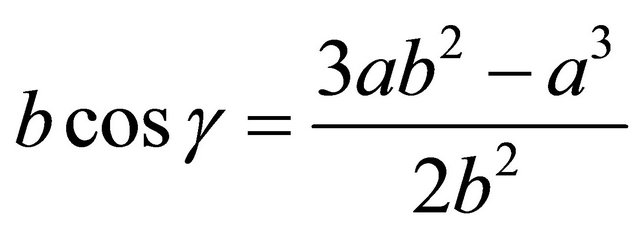
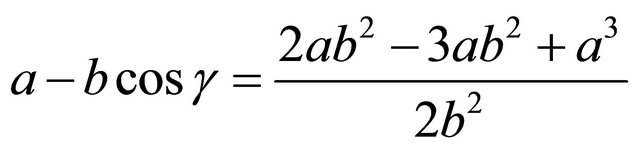
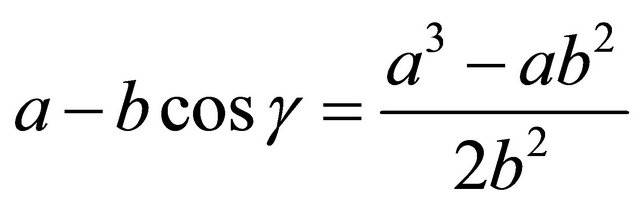
Substitute:

Simplify:

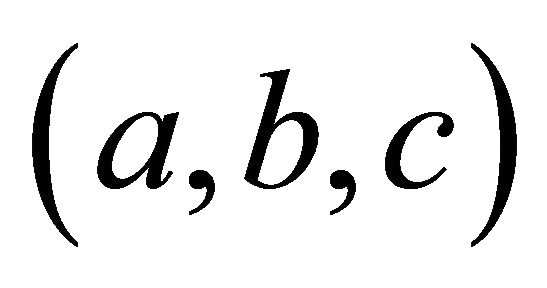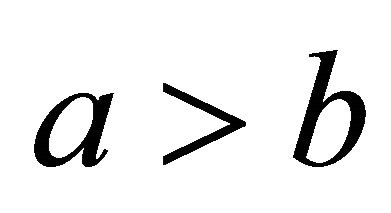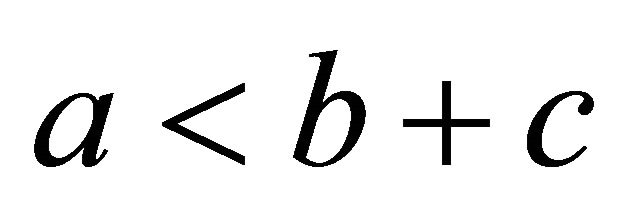Now we check that is a triangle. First, we already saw that, so. Second, to see that, we can reorganize the equation immediately above:

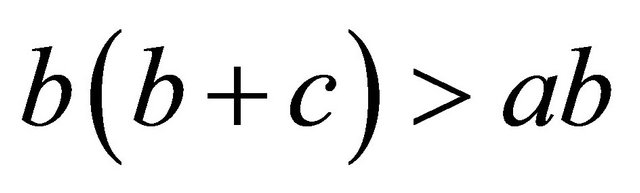
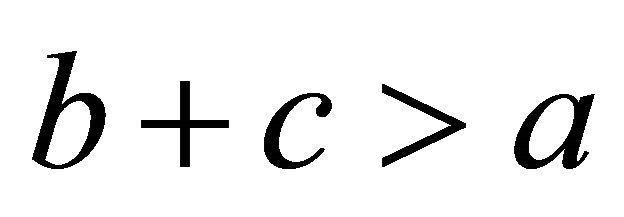
Third, we can continue to reverse the equations from the forward direction of the proof until we get back to

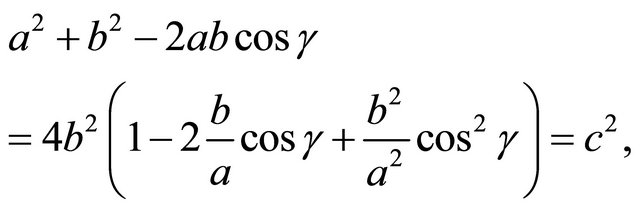
which gives us. It also shows by the Law of Cosines that the triangle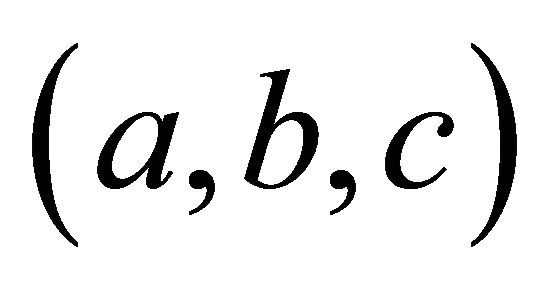, has angle 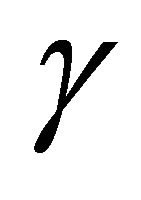opposite side c, so.

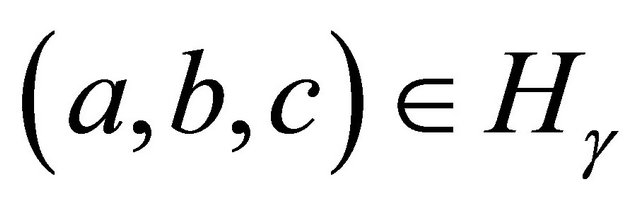Finally, we have already established the scaling equations

which show that

so 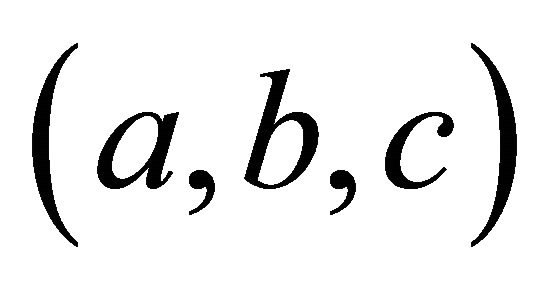has order three, as desired. ∎

Here are some sample applications of Theorem 4:

1) Let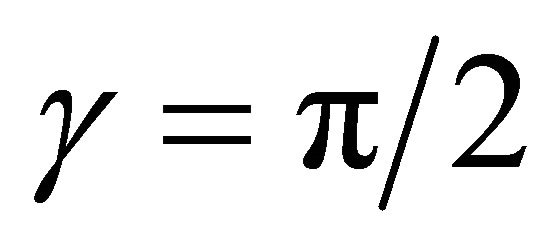. Then the cubic degenerates to 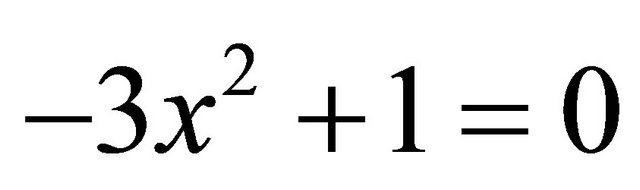, which has no rational solutions at all, and 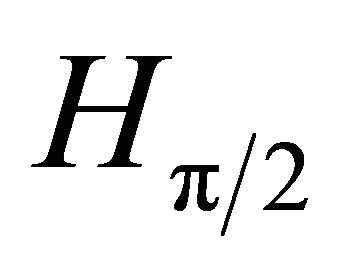has no point of order three.

2) Let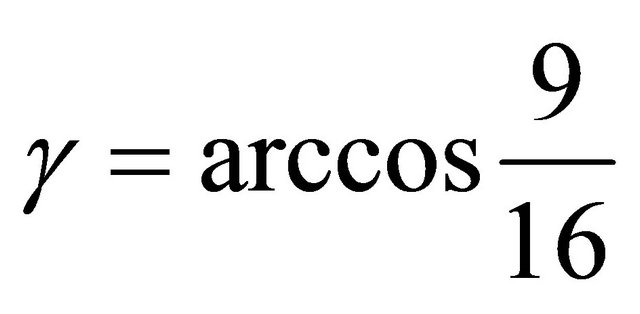. Then the cubic becomes

, which has the rational solution.

Following this through the proof above leads to the triangle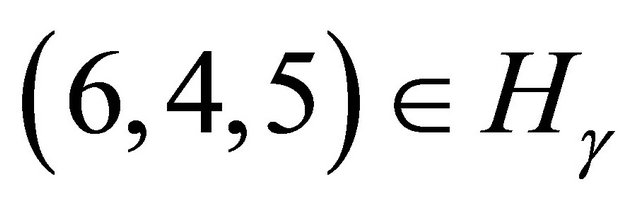, which has order three.

3) Let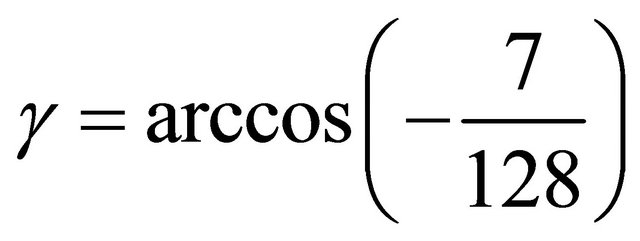. Then the cubic becomes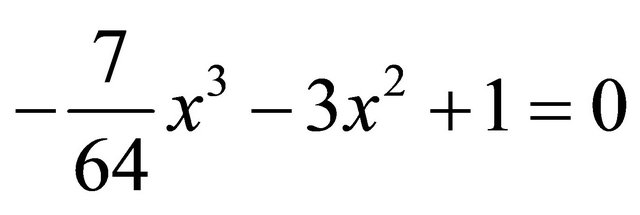, which has the rational solution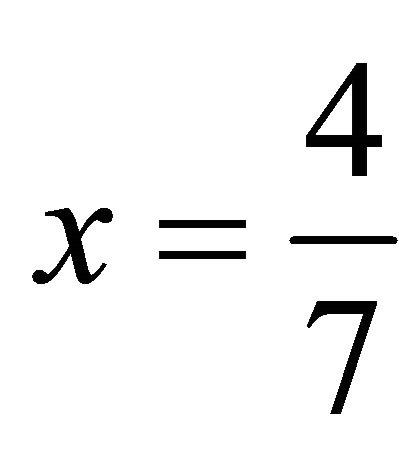. This leads to the triangle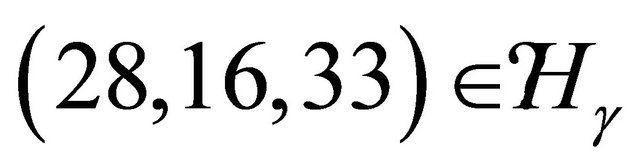, which has order three.

Although it is not quite so obvious, we have the same corollary as for two-torsion:

Corollary 5. The set of 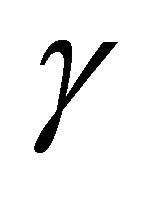for which 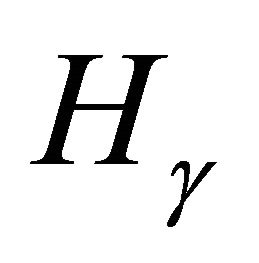contains a point of order three is dense in.

Proof. The rationals are dense in the interval 1/2 ≤ x ≤ 1, which, as noted above, is mapped continuously by

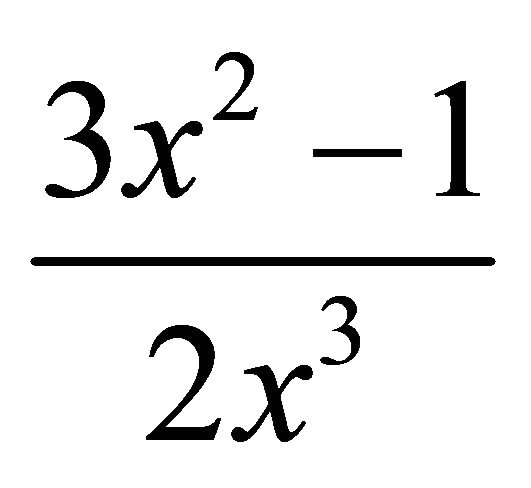onto 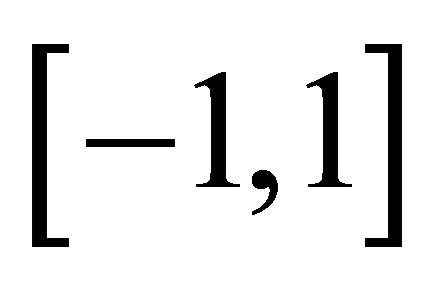and in turn by arccos onto 0 ≤ y ≤

π. Hence the set of 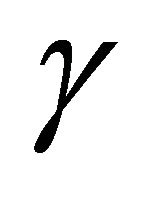corresponding to a rational x is dense in. ∎

4. Examples of Higher Order Torsion

We close with some examples of higher order torsion points in: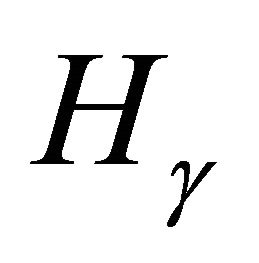

1) Let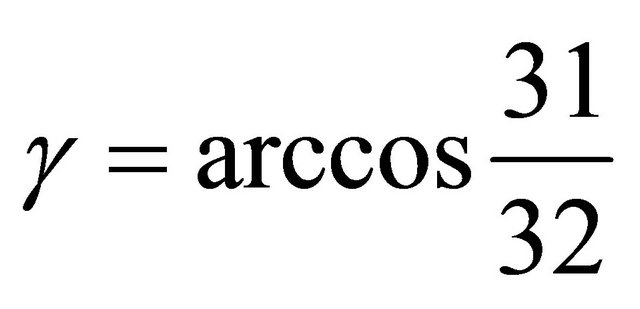. Then the triangle (10, 8, 3) has order four in.

2) Let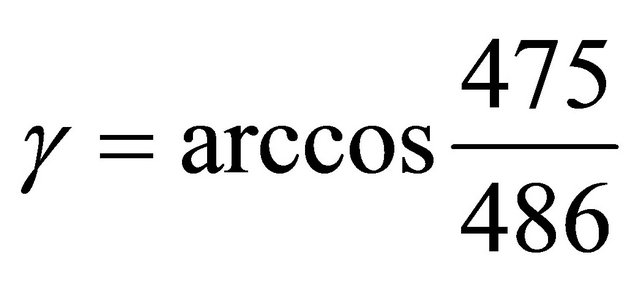. Then the triangle (105, 81, 31) has order five in.

3) Let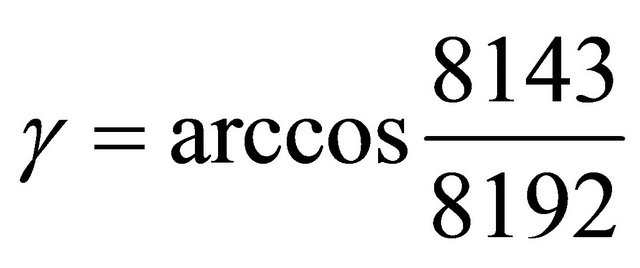. Then the triangle (1220, 1024, 231) has order six in.

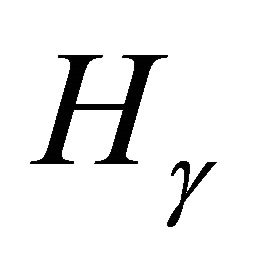I found these essentially by a brute force search on a computer, finding multiples of integral triangles and seeing which ones have finite order. As patterns start to emerge for smaller values, we can narrow and speed up the search for larger values by restricting to those triangles that satisfy similar patterns. In particular, there is a clear pattern in the values of b here: From computer-generated evidence, the pattern on the exponents seems to be genuine, but the pattern on the bases is a red herring: other examples of points of order six are

(5555, 3125, 3024) for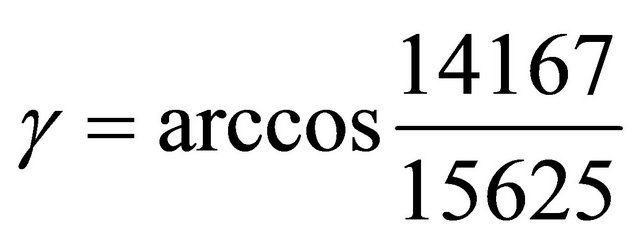, (17214, 7776, 12155) for, and (42833, 16807, 34320) for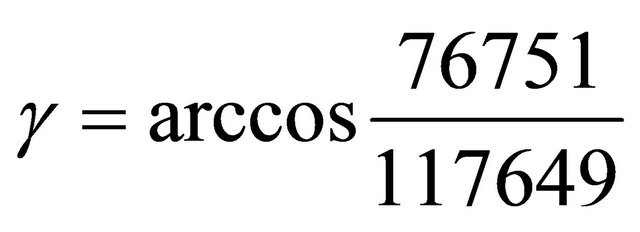. The consistent pattern seems to be that a point of order n must have the form (or, of course,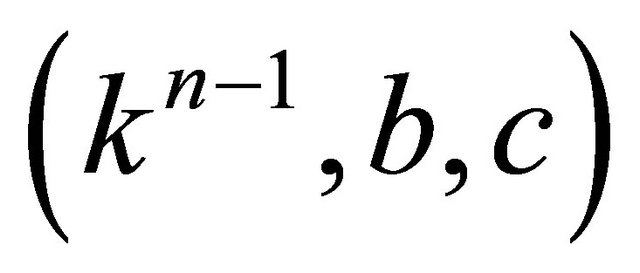), but I do not have a proof of this. I invite you to prove this or find a counterexample.

5. Conclusions and Further Questions

We have seen that although 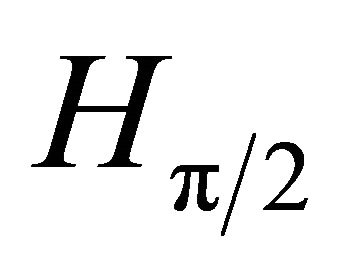is torsion-free, there are many values for which has torsion points of various orders. In fact, the set of 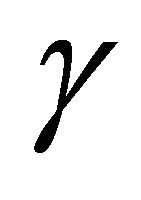for which 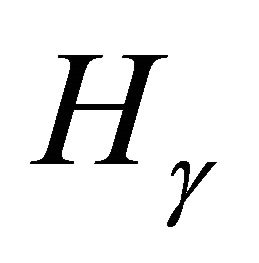has two-torsion (respectively, three-torsion) is dense in, and we can easily characterize all such in terms of conditions on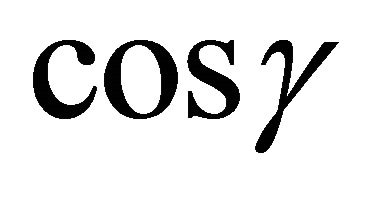. We have also seen that in such cases, 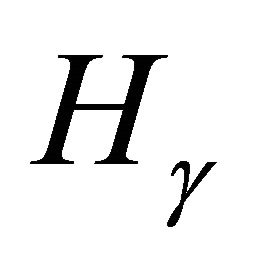contains a unique copy of 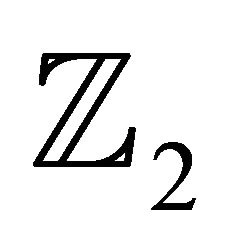(respectively,).

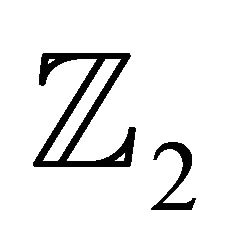There remain many intriguing open questions on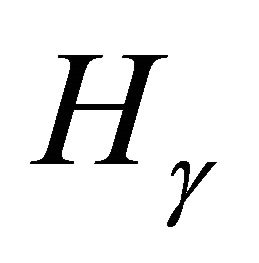. Obviously we would like to have a complete determination of the isomorphism type of 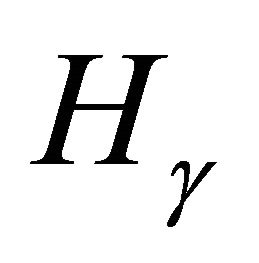for all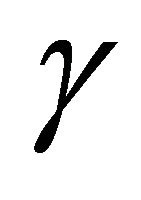, but since that doesn’t seem feasible in the near future, there are plenty of more approachable issues:

1) For what values of n do there exist 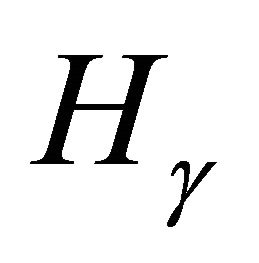with n-torsion?

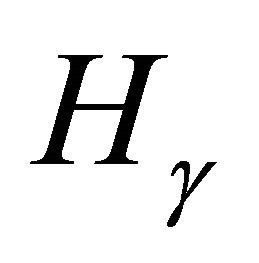2) For any n for which this is true, how can we characterize the for which has n-torsion?

3) Is the set of such dense in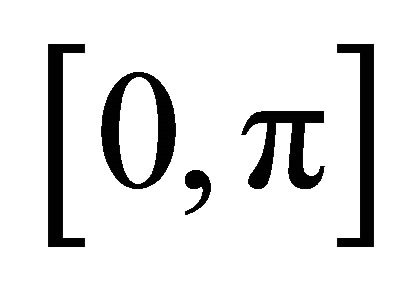? (Note that in all the examples of higher order torsion above, we had).

4) Is it possible for to contain more than one copy of?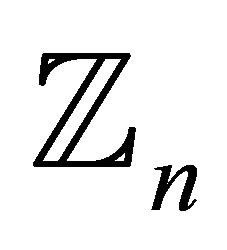

REFERENCES