Advances in Pure Mathematics
Vol.2 No.6(2012), Article ID:24984,4 pages DOI:10.4236/apm.2012.26067
Dynamic Systems of Shifts in the Space of Piece-Wise Continuous Functions
Department of Mathematics, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana
Email: ikedontwi@hotmail.com, obengdentehw@yahoo.com
Received July 24, 2012; revised September 17, 2012; accepted September 24, 2012
Keywords: Dynamic System; Shifts; Piecewise Continuous Functions; Compact Sets; Poisson Discontinuous Function
ABSTRACT
In this paper we embark on the study of Dynamic Systems of Shifts in the space of piece-wise continuous functions analogue to the known Bebutov system. We give a formal definition of a topological dynamic system in the space of piece-wise continuous functions and show, by way of an example, stability in the sense of Poisson discontinuous function. We prove that a fixed discontinuous function, f, is discontinuous for all its shifts,  whereas the trajectory of discontinuous function is not a compact set.
whereas the trajectory of discontinuous function is not a compact set.
1. Introduction
The interest in the study of Differential Equations with Impulse is increasing. Attempt to extend this study Dontwi [1] to known topological methods of the Theory of Dynamic Systems (DS) (see Sibiriskii [2], Levitan and Zhikov [3], Shcherbakov [4,5], Cheban [6,7]) brings into fore the necessity of studying DS of shifts in the space of piece-wise-continuous functions which are solutions of these equations.
In this paper we extend the study of Dynamical Systems of shifts in the space of piece-wise-continuous functions analogue to Bebutov Systems. We give a formal definition of a topological dynamic system in the space of piece-wise continuous functions and show, by way of an example, stability in the sense of poisson discontinueous function. We prove that a fixed discontinuous function, f, is discontinuous for all its shifts, 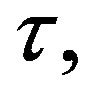 whereas the trajectory of discontinuous function is not a compact set. These should prepare the way for the introduction and application of notions of Recurrence motions of dynamic systems (Bronshtein [8], Pliss [9], Sacker and Sell [10], Sell [11]) to various trajectories of Differential Equations with Impulse (Distributions) (Hale [12], Cheban [13,14], and Dontwi [15]).
whereas the trajectory of discontinuous function is not a compact set. These should prepare the way for the introduction and application of notions of Recurrence motions of dynamic systems (Bronshtein [8], Pliss [9], Sacker and Sell [10], Sell [11]) to various trajectories of Differential Equations with Impulse (Distributions) (Hale [12], Cheban [13,14], and Dontwi [15]).
Ergodic dynamical system on the finite measure space and its kronecker factor were considered in Assani [16]. Pointwise convergence of ergodic averages along cubes was proved in Assani [17]. In Assani, Buczolich and Mauldin [18], negative solution to counting problem for measure preserving transformation was carried out. Full measures were treated in Assani [19]. A question of H. Furstenburg on the pointwise convergence of the averages was answered in Assani [20]. The pointwise convergence of some weighted averages linked to averages along cubes was studied in Assani [21]. Two questions related to the strongly continuous semigroup were answered in Assani and Lin [22]. Characteristics for certain nonconventional averages were studied in Assani and Presser [23]. Differentiable or smooth instead of topological gives a description of Differentiable Dynamics by Vries in [24].
Concepts such as metric spaces, normed spaces, convergence and homeomorphisms, compactness, and the Heine-Borel Theorem are considered to be known. In terms of discussing shifts this stems from several important applications of symbolic dynamics in the field of dynamical systems. It goes without telling that symbolic dynamics is a strong and formidable tool used in the study of dynamical system in Peyam [25]. The advantages that are gleaned from it are that the technique reduces a complicated system into a set of sequences. Mention should be made in the following passing: invariants, the Zeta function, Markov partition, and Homoclinic orbits.
2. Notions and Preliminaries
Let R and N be the set of real numbers and the set of natural numbers respectively, 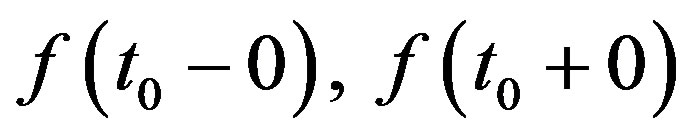 be the left and right sided limits of the function
be the left and right sided limits of the function 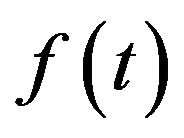 at the point
at the point 
We consider PC[R]—the space of piece-wise-continuous real-valued functions defined on the number line R with the following properties:
1) The set of points of discontinuity of every function 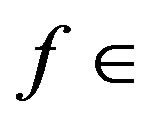 PC[R], represented as
PC[R], represented as 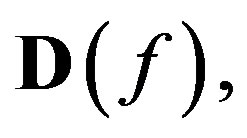 is either empty or has points of discontinuity of the first kind;
is either empty or has points of discontinuity of the first kind;
2) The point of discontinuity of every function, if it is more than one, is distinct from each other at a distance not less than some fixed positive number for a given function.
The jump or discontinuity of the function 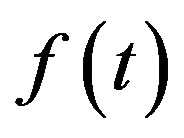 at the point
at the point 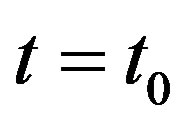 is the number
is the number
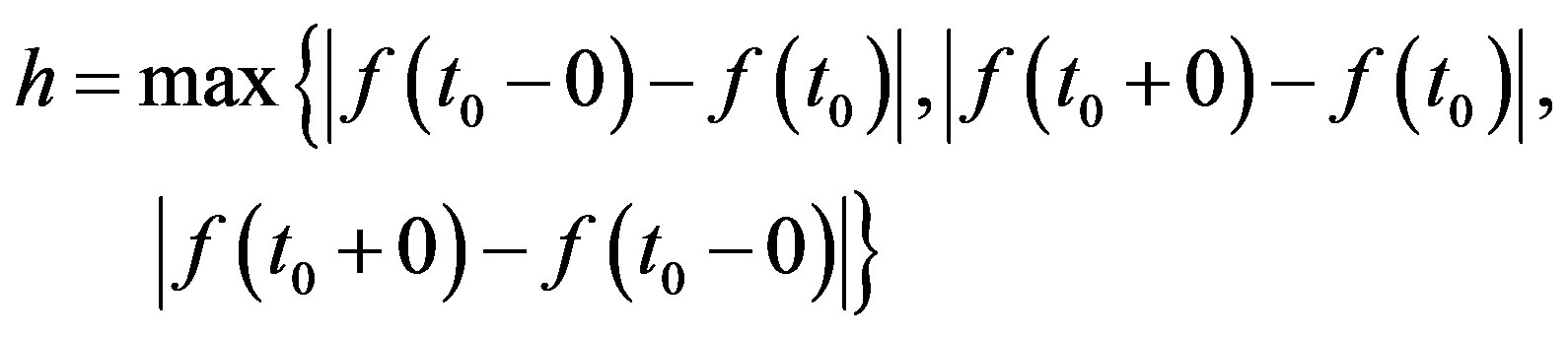
In PC[R], (or simply PC), we consider countable partitions of family of semi-norms
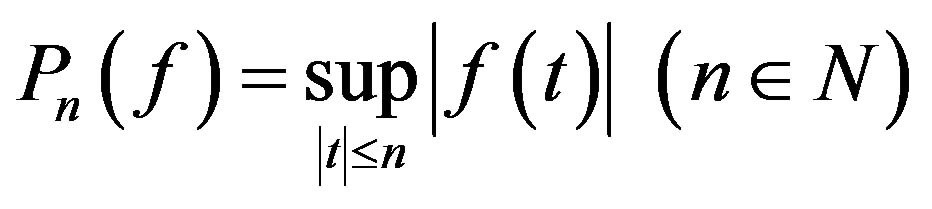
defined for every function  PC and induces metrizable topology in this space. Further we shall represent this metrizable space by PC.
PC and induces metrizable topology in this space. Further we shall represent this metrizable space by PC.
Definition 1.
An alphabet A is a set of symbols. A common example is 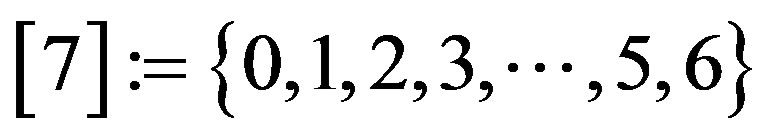 and in general
and in general

Definition 2.
Given an alphabet A, the full shift space is  (i.e. the space of sequence is from Z into A)
(i.e. the space of sequence is from Z into A)
Definition 3.
A homeomorphism,  from
from  to
to  is a continuous function
is a continuous function 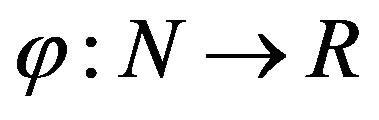 such that
such that 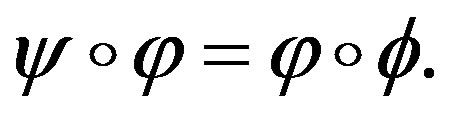
Definition 4.
Two dynamic systems 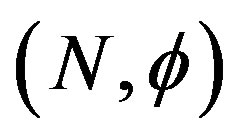 and
and 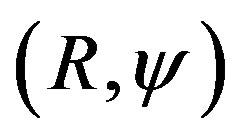 are topological conjugates if there exist a homeomorphism
are topological conjugates if there exist a homeomorphism  between them that is also a homeomorphism. This confirms that the subject of dynamical systems studies how a given system behaves throughout time which can be discrete or continuous iterates.
between them that is also a homeomorphism. This confirms that the subject of dynamical systems studies how a given system behaves throughout time which can be discrete or continuous iterates.
Definition 5.
An infinite subset T of A is compact if and only if every infinite subset of T has a limit point in T [26].
Definition 6.
A function  between topological spaces is called continuous, if
between topological spaces is called continuous, if  is open in X for every open
is open in X for every open  In Hoffman [27] the set of all continuous functions
In Hoffman [27] the set of all continuous functions  is often denoted by
is often denoted by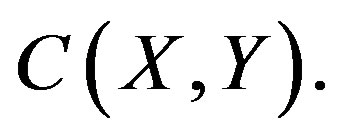
Remark 1.
The sequence of functions 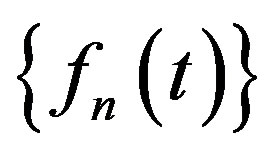 from PC is convergent if in PC there exist a function
from PC is convergent if in PC there exist a function 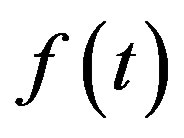 such that
such that 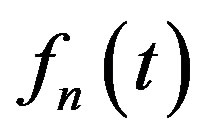 converges uniformly to
converges uniformly to 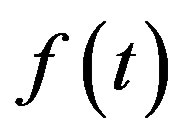 in every interval
in every interval 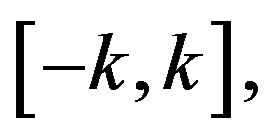 where
where 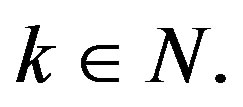 We write this in the form
We write this in the form

The following hold:
Lemma 1.
If the function  at the point
at the point 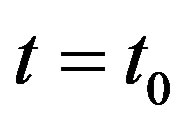 is a jump of magnitude
is a jump of magnitude 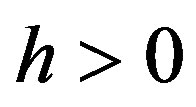 while the function
while the function  is continuous at this point, then for every
is continuous at this point, then for every 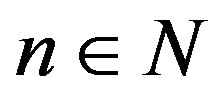 and
and 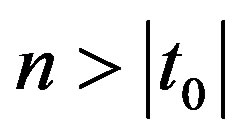 the following is true:
the following is true:
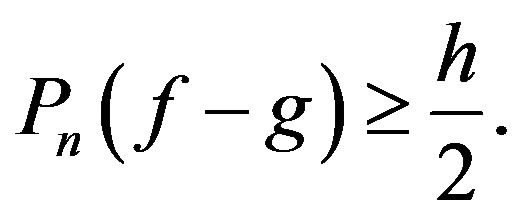
Lemma 2.
Let 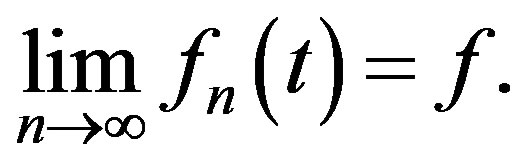 Then 1) If the function
Then 1) If the function  is discontinuous at the point
is discontinuous at the point 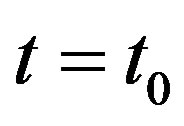 then all functions
then all functions 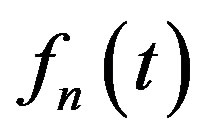 (except, maybe, for a finite number of points) are also discontinuous at the same point. As a consequence we have the following:
(except, maybe, for a finite number of points) are also discontinuous at the same point. As a consequence we have the following:
2) If beginning from some number, all functions  are continuous at the point
are continuous at the point  then the function
then the function 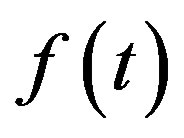 is also continuous at this point.
is also continuous at this point.
The reverse of the above statements hold.
Example 1.
Let 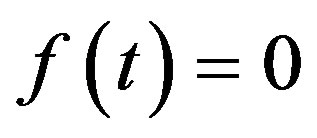 and
and
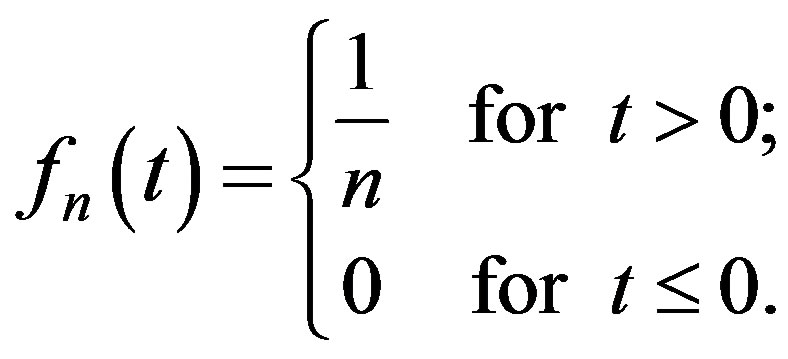
then 
Remark 2.
The space PC is not complete.
For any  and
and 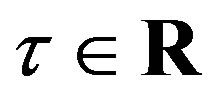 we represent by the symbol
we represent by the symbol  the shifts of the function
the shifts of the function 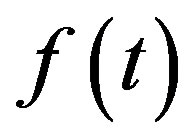 by
by 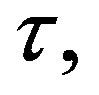 that is
that is 
Following Bebutov dynamic systems in the space PC we consider the family of shifts (or translates)
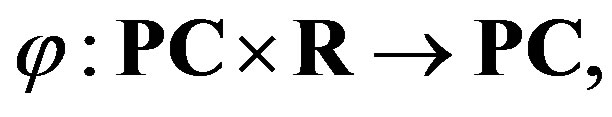 defined by the formula
defined by the formula
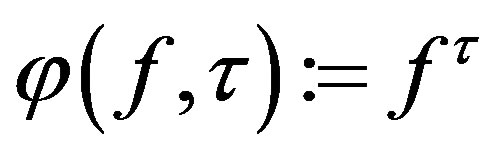 for all
for all 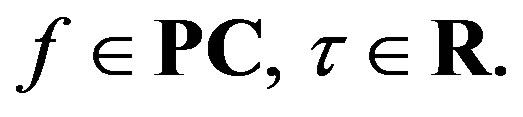
Definitions 1 to 5 serve as clues to the concepts discussed.
3. Main Results
Theorem 1.
The mapping  defined above satisfies the following conditions:
defined above satisfies the following conditions:
1)  for any
for any 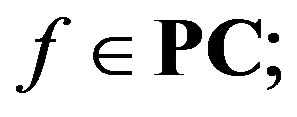
2) 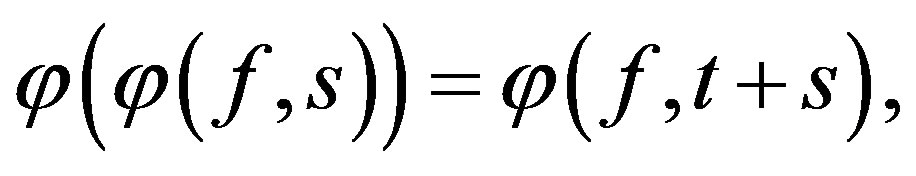 for any
for any  and
and 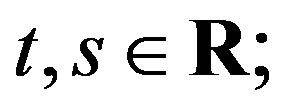
3) 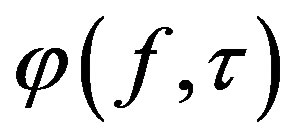 is continuous in f for any fixed
is continuous in f for any fixed  and for a fixed f-continuous function, the mapping
and for a fixed f-continuous function, the mapping 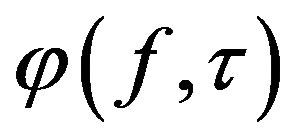 is continuous in
is continuous in  however, if for a fixed f it is a discontinuous function then
however, if for a fixed f it is a discontinuous function then  is discontinuous at all points of
is discontinuous at all points of 
Proof.
1) and 2) are obvious.
Continuity of 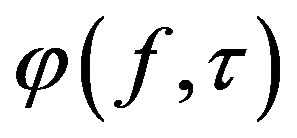 in f for a fixed
in f for a fixed  by Remark 1 implies uniform convergence of the function
by Remark 1 implies uniform convergence of the function 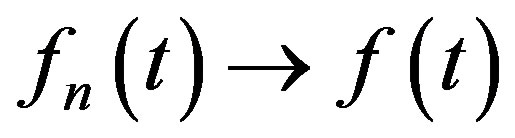 as
as  in every interval
in every interval ,
, 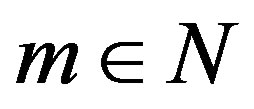 , which in turn implies uniform convergence of the function
, which in turn implies uniform convergence of the function  as
as 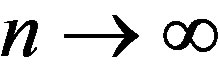 in every interval
in every interval 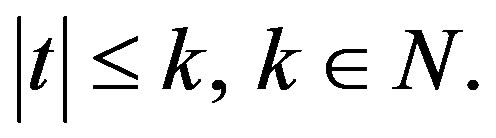
If  is a continuous function, then
is a continuous function, then  is continuous in
is continuous in  by the known property of Bebutov Dynamic System (Sell [11]) and is uniformly continuous in Obeng-Denteh [28].
by the known property of Bebutov Dynamic System (Sell [11]) and is uniformly continuous in Obeng-Denteh [28].
The motion corresponding to the continuous function f is continuous, and if it is discontinuous it will be discontinuous at every point.
Theorem 2.
For any arbitrary discontinuous function f from PC, its trajectory is not a compact set.
Proof.
Let f be any discontinuous function in PC. Consider
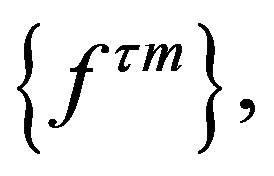 where
where  The given sequence converges point-wise to the function f of points of continuity of f. However, no sub-sequence of the given sequence converges to f in PC, and this means, in general it does not converge in PC.
The given sequence converges point-wise to the function f of points of continuity of f. However, no sub-sequence of the given sequence converges to f in PC, and this means, in general it does not converge in PC.
4. Conclusion
The topological dynamical system in the space of piecewise continuous functions has been shown by way of an example, as well as stability in the sense of Poisson discontinuous function. It has also been proved that a fixed discontinuous function, f, is discontinuous for all its shifts,  , whereas the trajectory of the discontinuous function is not a compact set.
, whereas the trajectory of the discontinuous function is not a compact set.
REFERENCES
- I. K. Dontwi, “One Class of Almost-Periodic Distributions and Some Properties,” Proceedings of Special SAMSA International Conference on Computers and Mathematics, University of Zimbabwe, Harrare, 1994, pp. 56-65.
- K. S. Sibiriskii, “Introduction to Topological Dynamics,” Redak-Izdat. Otdel. Akad. Nauk MSSR, Kishinev, 1970.
- B. N. Levitan and V. V. Zhikov, “Almost-Periodic Functions and Differential Equations,” Cambridge University Press, Cambridge, 1982.
- B. A. Shcherbakov, “Topological Dynamics and Poisson Stability of Solutions of Differential Equations,” Shtiintsa. Kishinev, 1972.
- B. A. Shcherbakov, “On Comparison by Character the Recurrence of the Motion of Dynamic Systems,” Journal of Differential Equations, Vol. 2, No. 7, 1975, pp. 1246- 1255.
- D. N. Cheban, “On Comparison of Points of Dynamic Systems by the Character of Their Returnability in the Limit,” Journal of Research in Algebra, Mathematical Analysis and Their Applications, Kishinev, Shtiintsa, 1997, pp. 66-71.
- D. N. Cheban, “Non-Autonomous Dissipative Dynamic Systems,” Soviet Mathematics: Doklady, Vol. 33, No. 1, 1986, pp. 207-210.
- I. U. Bronshtein, “Extension of Minimal Transformation Groups,” International Publications, Netherlands, 1975
- V. A. Pliss, “Nonlocal Problems in the Theory of Oscillations,” Academic Press, New York, 1966.
- R. J. Sacker and G. R. Sell, “Dichotomies for Linear Evolutionary Equations in Banach Spaces,” Journal of Differential Equations, Vol. 113, No. 1, 1994, pp. 17-67. doi:10.1006/jdeq.1994.1113
- G. R. Sell, “Topological Dynamics and Differential Equations,” Van Nostrand Reinhold Company, London, 1971.
- J. Hale, “Theory of Functional Differential Equations,” 2nd Edition, Springer-Verlag, New York, 1977. doi:10.1007/978-1-4612-9892-2
- D. N. Cheban, “Relations between the Different Types of Stability of the Linear Almost Periodical Systems in the Banach Space,” Electronic Journal of Differential Equations, Vol. 1999, No. 46, 1999, pp. 1-9. http://ejde.math.swt.edu or http://ejde.math.unt.edu
- D. N. Cheban, “Uniform Exponential Stability of Linear Periodic Systems in a Banach Space,” Electronic Journal of Differential Equations, Vol. 2001, No. 3, 2001 pp. 1-12. http://ejde.math.swt.edu or http://ejde.math.unt.edu
- I. K. Dontwi, “Bounded on R+ Generalized Functions and Some of their Properties,” Journal of Natural Sciences, Vol. 1, No. 2, 2001, pp. 83-92.
- I. Assani, “Spectral Characterisation of Wiener Wintner Dynamical Systems,” Ergordic Theory and Dynamical Systems, Vol. 24, No. 2, 2004, pp. 347-366.
- I. Assani, “Pointwise Convergence of Ergodic Averages along Cubes,” Journal d’Analyse Mathématique, Vol. 110, No. 1, 2010, pp. 241-269. doi:10.1007/s11854-010-0006-3
- I. Assani, Z. Buczolich and D. Mauldin, “An L1 Counting Problem in Ergodic Theory,” Journal d’Analyse Mathematique, Vol. XCV, 2005, pp. 221-241. doi:10.1007/BF02791503
- I. Assani, “Duality and the One-Sided Ergodic Hilbert Transform,” Contemporary Mathematics, 357, Chapel Hill Ergodic Workshops, 2004, pp. 81-90.
- I. Assani, “Pointwise Convergence of Nonconventional Averages,” Colloquium Mathematicum, Vol. 102, No. 2, 2005, pp. 245-262. doi:10.4064/cm102-2-6
- I. Assani, “Averages along Cubes for Not Necessarily Commuting Measure Preserving Transformations,” Contemporary Mathematics, Vol. 430, 2007, pp. 1-19.
- I. Assani and M. Lin, “On the One Sided Ergodic Hilbert Transform,” Contemporary Mathematics, Vol. 430, 2007, pp. 20-39. doi:10.1090/conm/430/08249
- I. Assani and K. Presser, “Pointwise Characteristics Factors for the Multiterm Return Times Theorem,” Ergordic Theory and Dynamical Systems, 2011.
- J. de Vries, “Elements of Topological Dynamics,” Kluwer Academic Publishers, Dordrecht, 1993.
- T. R. Peyam, “Shifts as Dynamical Systems,” 2010. http://math.berkeley.edu./~peyam/shifts.pdf
- W. F. Trench, “Introduction to Real Analysis,” Trinity University, San Antonio, 2003
- K. H. Hofmann, “Introduction to General Topology: An Introductory Course,” 2005.
- W. Obeng-Denteh, “On the Study of Topological Dynamical Systems,” Ph.D. Thesis, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana, 2012.

