World Journal of Condensed Matter Physics
Vol.3 No.1(2013), Article ID:28346,8 pages DOI:10.4236/wjcmp.2013.31015
Mathematical Modelling of Bloch NMR to Explain the Rashba Energy Features
![]()
Department of Physics, Federal University of Technology Minna, Minna, Nigeria.
Email: emetere@yahoo.com
Received September 7th, 2012; revised October 22nd, 2012; accepted November 9th, 2012
Keywords: Bloch NMR; Rashba Energy; Rashba Parameter; Quantum Well; Spin-Plit; Hole Spin Velocity
ABSTRACT
The Bloch NMR as an analytical tool was able to address the fundamental features in the learning of spintronics. Beside confirming past assertions on the Rashba spin-orbit interaction, thermal motion of hole and electron spin and features of the quantum well, it was also able to explain the condition necessary for Rashba splitting within the quantum well. When the Rashba energy is 43 meV, it modified the Ehrenfest’s theorem to hold for an external magnetic field. The confinement potential which is the strength of the Rashba spin-orbit interaction was shown to be controlled magnetically.
1. Introduction
The Bloch NMR model has over the years proven to be a good diagnostic tool for investigating properties of known quantities. For example, the Bloch NMR equations has shown good success in the study biological and physiological properties of living tissue [1,2]. Besides medical applications, the Bloch NMR equations were used to investigate the thermodynamic properties of system e.g. the Wegner distribution function [3]. Recently, the Bloch NMR was used to analyse the magnetic penetration depth of superconducting material and was also applied to explain the muon-spin [4].
The technological and computational prospects of semiconductor spintronics have been explored in various researches [5-10]. One of the notable works in the semiconductor spintronics is the Rashba term [11-13]. One of the major successes of the Rashba term is the measurement of the strength of spin splitting using the Rashba energy of split state and coupling parameter. The Rashba energies can be tuned by changing the composition parameters of the surface alloy [14,15] while the Rashba coupling parameter (αR) was calculated as 10−1 eVÅ for conventional narrow-gap semiconductor structures. Unfortunately, low Rashba coupling parameter do not supports the 2 d spintronics device. Early this year, a layered semiconductor (bismuth tellurohalides) was found to exhibit a large spin splitting [16] which was about 4.8 eV. The improvements on the spin-split extended to nonmagnetic material where the Rashba-Bychkov effect shows the possibility of producing spin-split energy bands in nonmagnetic materials without the application of any external magnetic field [17]. The Rashba splitting was believed to have been absent in quantum wells because quantum well states are standing waves [18], but was opposed by Stanley et al. [19]. The later proved that Rashba splitting occurs in the quantum well states II-V semiconductors. The giant spin splitting in semiconductor is dependent on the spin-orbit interaction [17,20] which is now referred to as the Rashba spin-orbit interaction [12]. The gaint spin splitting was first demonstrated on a noble metal [21,22] and further improved on in thin-film [23,24].
In this paper, the Bloch NMR equations were used as a diagnostic tool to analyze the Rashba energies state in a rotating magnetic frame. Derivations of operational equations were used to solve the Rashba energy with the mind set of investigating the conditions necessary for the presence of Rashba splitting in quantum wells and the possibility of controlling the confinement potential magnetically.
2. Theoretical Derivations
The following theoretical assumptions were made in order to incorporate the Bloch NMR into the spintronics device 1) The Rashba parameter was substituted for the spin coupling in the Bloch NMR because they both are synonymous in operation.
2) Let the excitation frequencies in each concept be the same 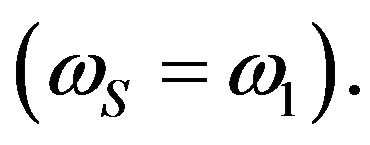
3) The macroscopic magnetization of the localized was equated with the equilibrium magnetization of the Bloch model.
4) Semiconductors have various electron-hole recombination rates [25,26]. The speed of the holes and electrons is assumed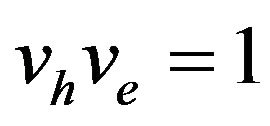 .
.
5) Both the g tends to 1, likewise the frequency difference between Larmor frequencies.
2.1. Spin Splitting Derivations
The Rashba energy and Rashba parameter are related in the equations shown below
 (1)
(1)
 (2)
(2)
 (3)
(3)
The magnetic potential introduced by Zeeman term
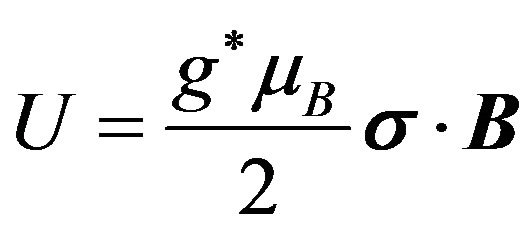 (4)
(4)
The resulting spin-splitting of s-type electron states is given by
 (5)
(5)
From Equations (1)-(5), Equation (6) was derived
 (6)
(6)
where ER = Rashba energy, αB = Rashba parameter, m* = effective mass, u = magnetic potential, σ = spin index, Pauli spin matrices, for electric spin, it is given as
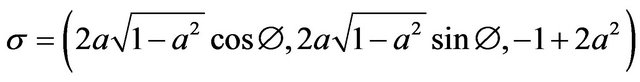
where a = lattice constant, g = g-factor. μB = mobility.
2.2. Bloch NMR Derivation Model
In this section, a mathematical algorithm to describe in detail the translational mechanical properties of the Bloch NMR equation was developed. A sample of atomic crystal structure is analyzed by the x, y, z component (in the rotating frame) of magnetization given by the Bloch equations which may be written as follows
 (7)
(7)
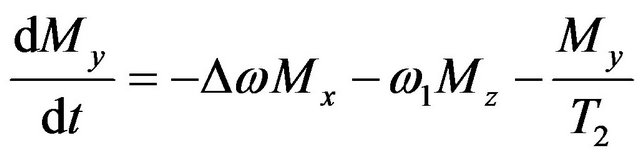 (8)
(8)
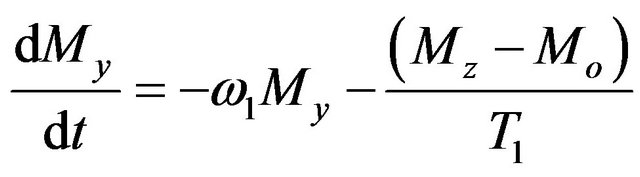 (9)
(9)
where  the frequency difference between Larmor frequency and frame of reference,
the frequency difference between Larmor frequency and frame of reference, 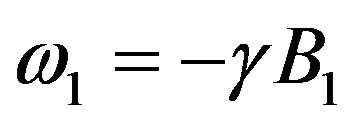 is the Rabi frequency,
is the Rabi frequency, 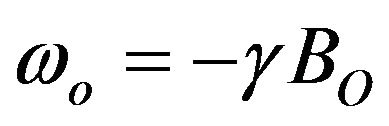 is the Larmor frequency, Mx, My are the transverse magnetization, Mz is the longitudinal magnetization, Mo is the equilibrium magnetization. The movement of the holes and electrons is assumed to move at a velocity Ve and Vh and at distances Lh & Le from the conduction and valence bands.
is the Larmor frequency, Mx, My are the transverse magnetization, Mz is the longitudinal magnetization, Mo is the equilibrium magnetization. The movement of the holes and electrons is assumed to move at a velocity Ve and Vh and at distances Lh & Le from the conduction and valence bands.
 (10)
(10)
 (11)
(11)
 (12)
(12)
where 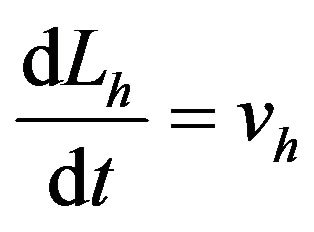 and
and 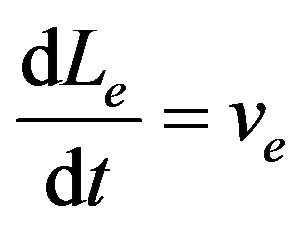
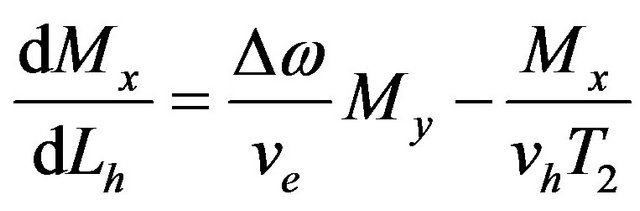 (13)
(13)
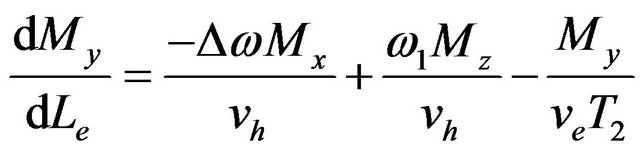 (14)
(14)
 (15)
(15)
The solution of the above equations can be arranged in matrix form as shown below
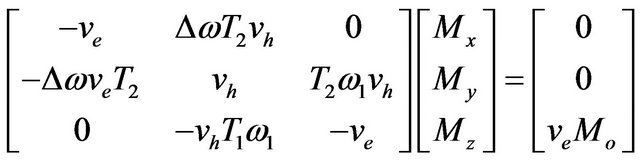 (16)
(16)
The matrix multiplication as shown below leads to the steady solutions of the Bloch equations in the rotating frame of reference are shown below
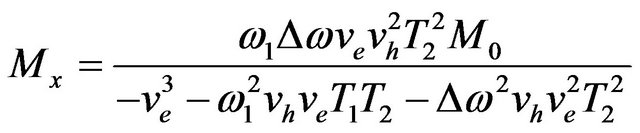 (17)
(17)
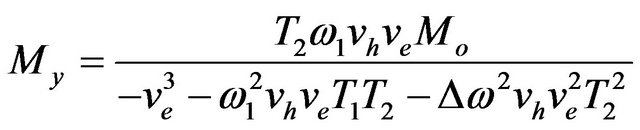 (18)
(18)
 (19)
(19)
These solutions directly give the frequency response of the magnetization. This idea gives the possibilities of quantitatively calculating the measured signal if a spin system is characterized by relaxation times T1 and T2. The term 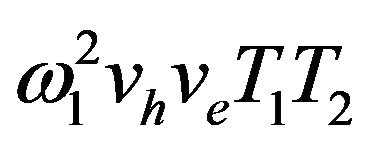 is proportional to the radio frequency power P. At the state of no saturation i.e. for low power P, this term
is proportional to the radio frequency power P. At the state of no saturation i.e. for low power P, this term 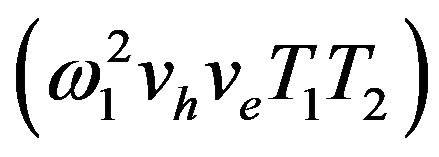 is small
is small 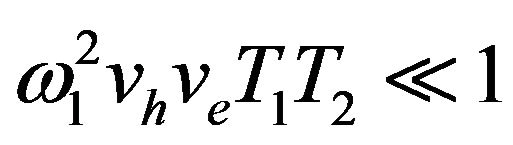 .
.
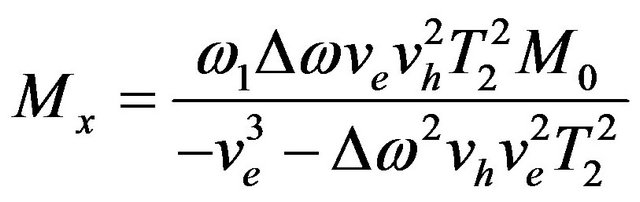 (20)
(20)
 (21)
(21)
2.3. Operational Equations
The operational equations used for the simulations were worked out and systems of equations were generated. Equations (6), (20) and (21) yield
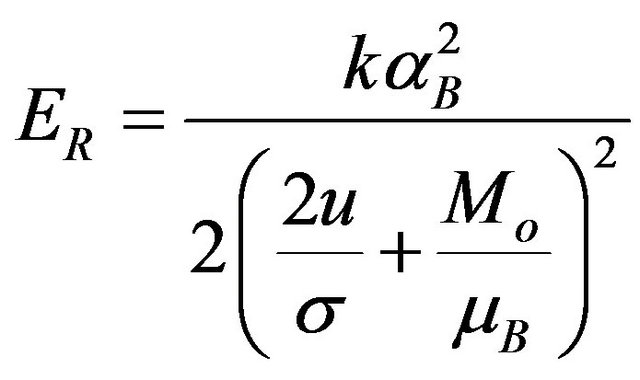 (22)
(22)
 (23)
(23)
where 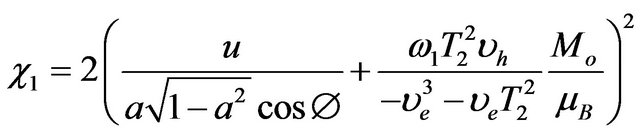
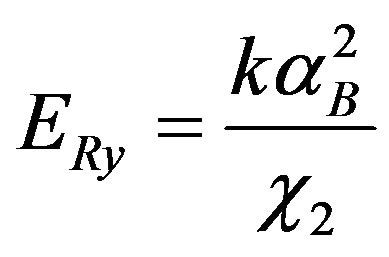 (24)
(24)
where 
Equations (17)-(19) yield when 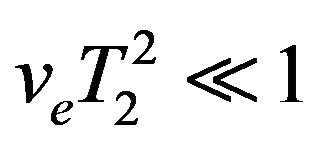
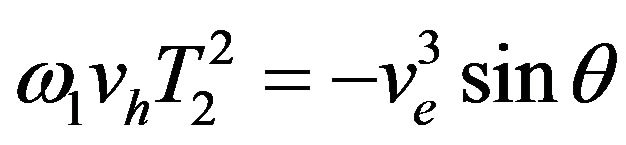 (25)
(25)
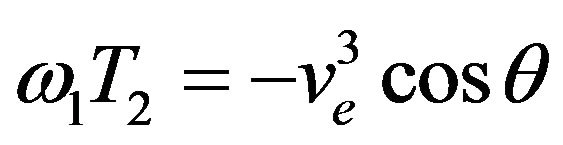 (26)
(26)
 (27)
(27)
Applying Equations (23)-(27)
 (28)
(28)
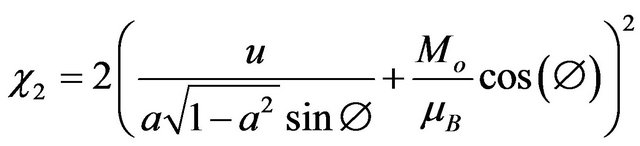 (29)
(29)
Ploting the first and second term of Equations (28) and (29) where 
The Rashba energy along the vertical and horizontal axes are represented diagrammatically (shown in Figure 1) which satisfies the mathematical expression  .
.
Figure 1. Rashba energy representation.
3. Simulations of Derivations
In this section, the simulations of Equations (22)-(24) under various conditions e.g. the time relaxations and magnetic moments. Time relaxations of 9 ns was applied (Laura Fanea et al., 2011) to investigate the behavior of the Rashba energy with respect to its longitudinal and transverse component.
4. Results and Discussion
Thermal motion of the hole was investigated in Figure 2 where the hole velocity was plotted against the angle of propagation at a relaxation time 9 × 10−9 s. Its results was in accordance with past papers [27,28] which was interpreted that the stochastic modulation of the interaction between the heavy and light hole sub-bands may induce a nonadiabatic transitions between them, which may eventually lead to J-relaxation and dephasing. In Figure 3, the focus was to which type of character is dominant among the subbands. In accordance to the graphical expression given by Winkler [29] it was discovered that the features of Figure 3 is a heavy hole character. Figure 4 investigated the relationship between the potential and the spin mobility within the system. The direction of the wavelike structure gives an asymmetric double peak structure which shows that energy exist between the peaks which was as a result of the perpendicular magnetic field. An in-plane inversion asymmetry can induce a contribution from an in-plane potential gradient, which can strongly enhance the spin splitting [22]. Figures 5 and 6 explain more on effect of the external magnetic fields on the holes or electron in the quantum well. Actually, Figure 5 supports the idea that quantum well states are standing waves and should therefore show no Rashba splitting while Figure 6 supports that the Rashba splitting occurs in the quantum well state (two strange events). One of the objectives of this paper was to investigate the conditions necessary for the Rashba splitting within the quantum well. Figures 7 and 8 are similar in shape i.e. showing the strength of the splitting. Figures 9 and 10 show the Rashba energies at ground state (in which was calculated at about ≥43 meV) which have two branches synonymous to the spin up state and the spin down state.
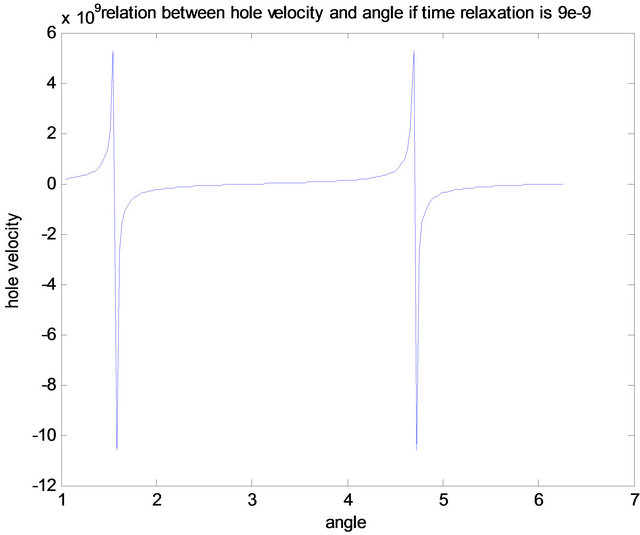
Figure 2. Hole velocity-angle relationship when the time relaxation is 9 × 10−9 s.
 (a)
(a)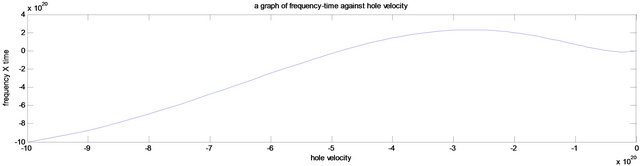 (b)
(b)
Figure 3. (a) Frequency-time versus angular change; (b) Frequency-time versus hole velocity.
Unlike the findings of Eerdunchaolu et al. [30] an increase in the Rashba energy makes no significant change in χ1 & χ2 (which is described as the height). More importantly, it reveals that Rashba split of orbit interaction effect is not dependent on the height in the y direction. This is because the effective magnetic field which is produced by spin-orbit coupling (due to the lack of structure inversion symmetry) is approximately perpendicular to the electron momentum in the quantum ring. Figure 11 shows that electron wave function bound in a quantum well in the presence of an external (or built-in) field e.g. Mx, My or Mz. Very much like the reaction of the electric
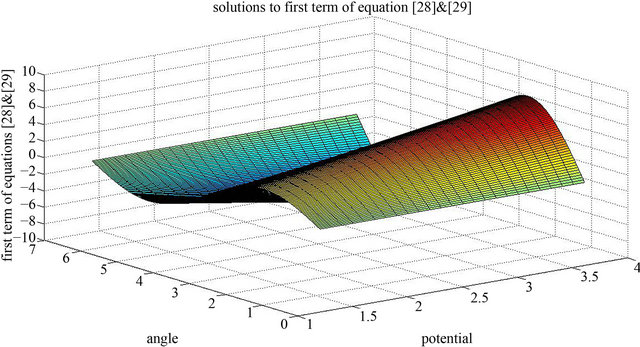
Figure 4. First term solutions of Equations (28) and (29).
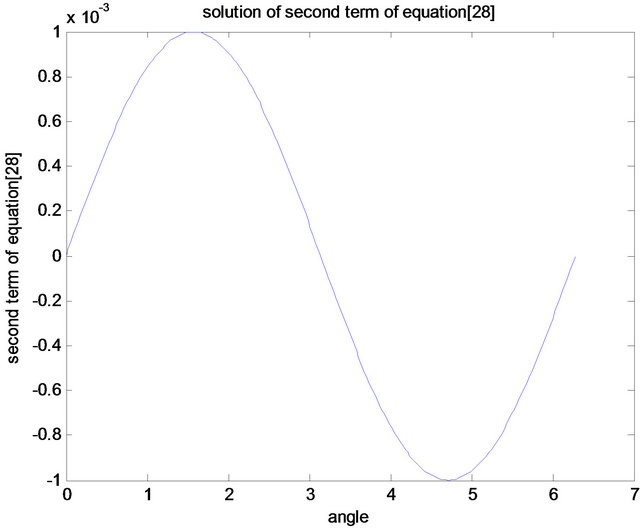
Figure 5. Second term solution of Equation (23).
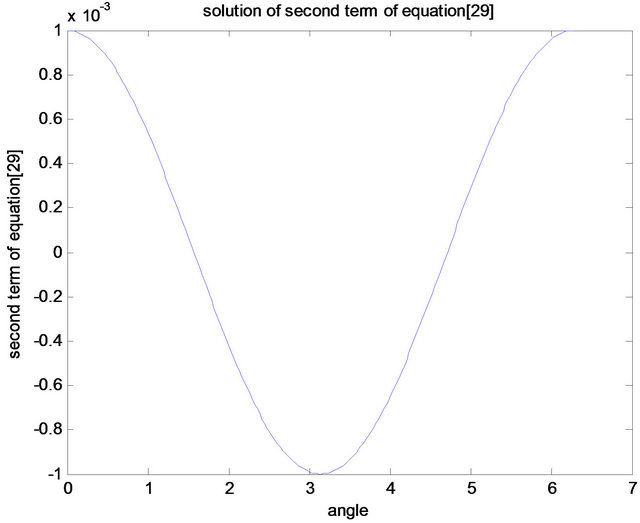
Figure 6. Solutions of the second term of Equation (24).

Figure 7. Graphical solution of χ1 in Equation (23).
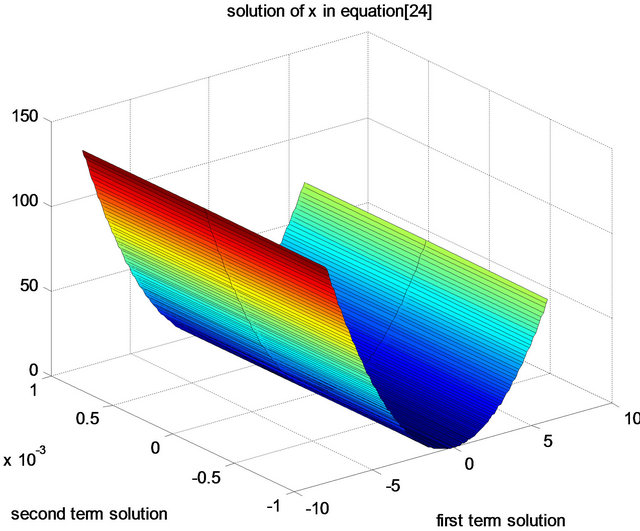
Figure 8. Graphical solution of χ2 in Equation (24).

Figure 9. Solution of the Rashba energy of the horizontal axis.
fields in the quantum well, the behavioral features of the effective magnetic field in the conduction band (upper part of Figure 11) and valence band (lower part of Figure 11)) is the sum of the magnetic field and the contributions due to the position dependence of the conduction band. In other words, the modification of Ehrenfest’s theorem becomes necessary because it is the magnetic field in the valence band that controls the Rashba spin splitting of electron states. Figure 12 gives a joint feature of Figures 5 and 6 which may suggest the possibility of the ideas of Petersen et al. [18] and Stanley et al. [19] occurring simultaneously within the quantum well.
5. Conclusion
The Bloch NMR model has been proven to be efficient in analyzing the fundamentals of spintronics. It was discovered that an increase in the Rashba energy makes no sig-

Figure 10. Solution of the Rashba energy of the vertical axis.

Figure 11. The nature of fields along the axes.
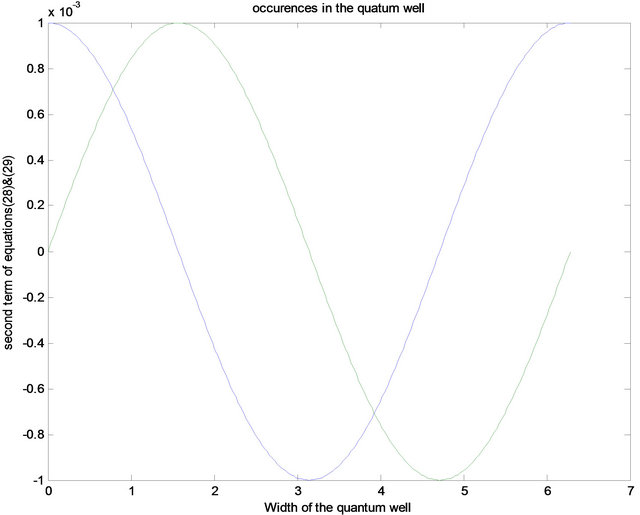
Figure 12. Occurrences in the quantum well state.
nificant changes in χ1 & χ2 (which was described as height). This result, makes the Rashba split of orbit interaction effect independent on the height along the y direction as shown in Figures 9 and 10. Furthermore, this led to the alteration of Ehrenfest’s theorem (which originally applies to the external electric fields), but now applies to the external magnetic field. Therefore, the confinement potential which is the strength of the Rashba spin-orbit interaction can also be controlled magnetically. This idea may be expatiated upon based on further research. Also the Bloch NMR was also effective to analyze the quantum well i.e. even though it is a standing wave, it could still experience Rashba splitting when the quantized electron energy Ee ≥ 1 meV and the length of the quantum well is 6 nm.
6. Appreciation
This work is self-funded. I appreciate Mrs. Jennifer Emetere for editing the script. I appreciate the Head of Physics Department of the above named institution.
REFERENCES
- O. B. Awojoyogbe, “A Mathematical Model of Bloch NMR Equations for Quantitative Analysis of Blood Flow in Blood Vessels with Changing Cross-section II,” Physica A: Statistical Mechanics and Its Applications, Vol. 323, 2003, pp. 534-550. doi:10.1016/S0378-4371(02)02025-3
- O. B. Awojoyogbe, “Analytical Solution of the Time Dependent Bloch NMR Equations: A Translational Mechanical Approach,” Physica A: Statistical Mechanics and Its Applications, Vol. 339, No. 3-4, 2004, pp. 437- 460. doi:10.1016/j.physa.2004.03.061
- E. P. Wigner, “On the Quantum Correction for Thermodynamic Equilibrium,” Physical Review, Vol. 40, No. 5, 1932, pp. 749-759. doi:10.1103/PhysRev.40.749
- U. E. Uno and M. E. Emetere, “Analysis of the High Temperature Superconducting Magnetic Penetration Depth Using the Bloch NMR Equations,” Global Engineers and Technologist Review, Vol. 2, No. 1, 2012, pp. 14-21.
- C. Benett and D. Di Vincenzo, “Quantum Information and Computation,” Nature, Vol. 404, 2000, pp. 247-253. doi:10.1038/35005001
- S. Yuasa, T. Nagahama, A. Fukushima, Y. Suzuki and K. Ando, “Giant Room-Temperature Magnetoresistance in Single-Crystal Fe/MgO/Fe Magnetic Tunnel Junctions,” Nature Materials, Vol. 3, No. 12, 2004, pp. 868-871. doi:10.1038/nmat1257
- S. Parkin, C. Kaiser, A. Panchula, P. Rice, B. H. M. Samant and S. H. Yang, “Giant Tunnelling Magnetoresistance at Room Temperature with MgO (100) Tunnel Barriers,” Nature Materials, Vol. 3, 2004, pp. 862-867. doi:10.1038/nmat1256
- T. Dietl, “Magnetic Anisotropy and Domain Structure in Carrier-Controlled Ferromagnetic Semiconductors,” Journal of Physics: Condensed Matter, Vol. 16, No. 48, 2004, p. S5471. doi:10.1088/0953-8984/16/48/001
- T. Dietl, “Magnetic Anisotropy and Domain Structure in Carrier-Controlled Ferromagnetic Semiconductors,” Proceedings 27th International Conference on Physics of Semiconductors, Flagstaff, 2004, pp. 56-60.
- F. H. L. Koppens, et al., “Driven Coherent Oscillations of a Single Electron Spin in a Quantum Dot,” Nature, Vol. 442, 2006, pp. 766-771. doi:10.1038/nature05065
- Z. Wilamowski, W. Jantsch, N. Sandersfeld, M. Muhlberger, F. Schaffler and S. Lyon, “Spin Relaxation and g-Factor of Two-Dimensional Electrons in Si/SiGe Quantum Wells,” Physica E: Low-Dimensional Systems and Nanostructures, Vol. 16, No. 2, 2003, pp. 111-115. doi:10.1016/S1386-9477(02)00582-9
- Y. Bychkov and E. I. Rashba, “Oscillatory Effects and the Magnetic Susceptibility of Carriers in Inversion Layers,” Journal of Physics C: Solid State Physics, Vol. 17, No. 33, 1984, pp. 6039-6045.
- E. I. Rashba, “Theory of Electrical Spin Injection: Tunnel Contacts as a Solution ofthe Conductivity Mismatch Problem,” Physical Review B, Vol. 62, No. 24, 2000, pp. R16267-R16270. doi:10.1103/PhysRevB.62.R16267
- F. Meier, V. Petrov, S. Guerrero, C. Mudry, L. Patthey, J. Osterwalder and J. H. Dil, “Unconventional Fermi Surface Spin Textures in the BixPb1−x/Ag(111) Surface Alloy,” Physical Review B, Vol. 79, No. 24, 2009, pp. 241408-241412. doi:10.1103/PhysRevB.79.241408
- J. Nitta, T. Akazaki and H. Takayanagi, “Gate Control of Spin-Orbit Interaction in an Inverted In0.53Ga0.47As/ In0.52Al0.48As Heterostructure,” Physical Review Letters, Vol. 78, No. 7, 1997, pp. 1335-1338. doi:10.1103/PhysRevLett.78.1335
- S. V. Eremeev, I. A. Nechaev, Y. M. Koroteev, P. M. Echenique and E. V. Chulkov, “Ideal Two-Dimensional Electron Systems with a Giant Rashba-Type Spin Splitting in Real Materials: Surfaces of Bismuth Tellurohalides,” Physical Review Letters, Vol. 108, No. 24, 2012, pp. 246802-246807. doi:10.1103/PhysRevLett.108.246802
- Y. A. Bychkov and E. I. Rashba, “Properties of a 2D Electron Gas with Lifted Spectral Degeneracy,” JETP Letters, Vol. 39, No. 2, 1984, pp. 78-83.
- L. Petersen and P. Hedegard, “A Simple Tight-Binding Model of Spin-Orbit Splitting of Sp-Derived Surface States,” Surface Science, Vol. 459, No. 1-2, 2000, pp. 49-56. doi:10.1016/S0039-6028(00)00441-6
- J. P. Stanley, N. Pattinson, C. J. Lambert and J. H. Jefferson, “Rashba Spin-Splitting in Narrow Gap III-V Semiconductor Quantum Wells,” Physica E: Low-Dimensional Systems and Nanostructures, Vol. 20, No. 3-4, 2004, pp. 433-435. doi:10.1016/j.physe.2003.08.052
- M. I. Dyakonov and V. Y. Kachorovskii, “Spin Relaxation of Two Dimensional Electrons in Noncentrosymetric Semiconductors,” Soviet Physics: Semiconductors, Vol. 20, 1986, pp. 110-116.
- D. Pacilé, C. R. Ast, M. Papagno, C. Da Silva, L. Moreschini, M. Falub, A. P. Seitsonen and M. Grioni, “Electronic Structure of an Ordered Pb∕Ag(111) Surface Alloy: Theory and Experiment,” Physical Review B, Vol. 73, No. 24, 2006, pp. 245429-245435. doi:10.1103/PhysRevB.73.245429
- C. R. Ast, K. Kern and M. Grioni, “Giant Spin Splitting through Surface Alloying,” Physical Review Letters, Vol. 98, No. 18, 2007, pp. 186807-186811. doi:10.1103/PhysRevLett.98.186807
- K. He, T. Hirahara, T. Okuda, S. Hasegawa, A. Kakizaki and I. Matsuda, “Spin Polarization of Quantum Well States in Ag Films Induced by the Rashba Effect at the Surface,” Physical Review Letters, Vol. 101, No. 10, 2008, pp. 107604-107608. doi:10.1103/PhysRevLett.101.107604
- E. Frantzeskakis, S. Pons, H. Mirhosseini, J. Henk, C. R. Ast and M. Grioni, “Tuning of Spin-Gaps at Silicon Interfaces,” Physical Review Letters, Vol. 101, No. 19, 2008, pp. 196805-196809. doi:10.1103/PhysRevLett.101.196805
- R. F. Pierret, “Semiconductor Device Fundamentals,” Prentice Hall, New York, 1995.
- P. Harrison, “Quantum Wells, Wires and Dots,” Wiley, New York, 2005. doi:10.1002/0470010827
- Y. A. Serebrennikov, “Single-Hole Spin Dephasing in Bulk Crystals,” Physical Review B, Vol. 71, No. 23, 2005, pp. 233202-233206. doi:10.1103/PhysRevB.71.233202
- D. Culcer and R. Winkler, “Spin Polarization Decay in Spin-1/2 and Spin-3/2 Systems,” Physical Review B, Vol. 76, No. 19, 2007, pp. 195204-195210. doi:10.1103/PhysRevB.76.195204
- R. Winkler, “Spin-Orbit Coupling Effects in Two-Dimensional Electron and Hole Systems,” Springer-Verlag Berlin Heidelberg, New York, 2003. doi:10.1007/b13586
- Eerdunchaolu, W. Xin and Y.-W. Zhao, “Influence of Rashba SOI and Polaronic Effects on the Ground-State Energy of Electrons in Semiconductor Quantum Rings,” Chinese Physics Letters, Vol. 27, No. 1, 2010, pp. 017201- 017201. doi:10.1088/0256-307X/27/1/017201

