Atmospheric and Climate Sciences
Vol.04 No.05(2014), Article ID:52479,14 pages
10.4236/acs.2014.45083
Consistency in Z-R Relationship Variability Regardless Precipitating Systems, Climatic Zones Observed from Two Types of Disdrometer
Bakary Bamba1, Abé Delfin Ochou1, Eric-Pascal Zahiri1, Modeste Kacou1,2
1Laboratory of Atmospheric Physics and Fluid Mechanics, University Félix Houphouët-Boigny, Abidjan, Côte d’Ivoire
2Geosciences Environment Toulouse (GET), University Paul Sabatier of Toulouse III, Toulouse, France
Email: ochoud@yahoo.com, ochou.delfin@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 October 2014; revised 30 November 2014; accepted 17 December 2014
ABSTRACT
Data from rain Drop Size Distributions gathered on five sites in Africa as well as those of the pilot site in Kourou (French Guyana, South America), located in different climatic zones, and collected by two types of disdrometer (the impact JW RD-69 disdrometer and the Optical Spectro-Pluvi- ometer, OSP) are used to study the consistency of the reflectivity factor-rain rate at the ground (Z-R) relationship variability. The results clearly confirm that the relationship Z-R knows a large spatial variability, from a type of precipitation to another and within the same precipitation regard- less the type of disdrometer used for DSD measurements. Base on the similarity of the relations reflectivity factor-rain rate and ratio median volume diameter over the total number of drops-rain rate, the variability of the Z-R coefficients (A, b) through the simultaneously implication of the size and number of drops which characterize the DSD was exhibited. It was shown that the relation- ships A-α and b-β designed to understand the involvement of parameters D0 and NT of DSD in the variability of the relationship Z-R are similar regardless the types of disdrometer used. However, the relations A-α in the Sahelian region appear to deviate from those of Guinean, equatorial and Soudanian zones. The plausible reasons were discussed.
Keywords:
Drop Size Distributions, Consistency in Z-R Relationship Variability, Squall Lines, Thunderstorm, Stratiform Rain, JW RD-69 Disdrometer, Optical Spectro-Pluviometer OSP

1. Introduction
The measurement of the raindrop size distribution commonly called DSD is important to characterize rainfall from cloud systems through some integrated parameters and to infer also radar parameters. From these meas- urements, establishment of a relationship between the rain rate R (mm/h) and the radar reflectivity factor Z (mm6∙m−3) is useful for remote sensing estimation of rain by radar [1] - [7] .
Numerous studies showed that empirical function of the form Z = ARb describes well this relationship [8] - [13] . Authors such as, Sauvageot and Lacaux [2] , Atlas et al. [14] , Maki et al. [15] and more recently Mou- mouni et al. [16] , Ochou et al. [17] and T. Islam et al. [7] among others, indicated a great variability in space and time of this relationship according to local climatological, dynamic conditions and rain type.
In the context of increasing the quality of the radar measurements, therefore to reduce the errors in the rainfall estimation from Z-R relationship, authors suggested to associate with each type of precipitation (convective or stratiform type), an appropriate Z-R relation [18] - [24] . Thus, different investigations carried out on the A and b coefficients of the necessary relationship Z-R have allowed identifying two schools. The first one showed that the coefficient A is higher in the convective part than in the stratiform part of a same squall line [21] whereas the second one, sustained by authors such as Tokay and Short [20] , Atlas et al. [14] , Narayana et al. [25] , Maki et al. [15] and T. Islam et al. [7] , indicated that coefficient A is higher in stratiform than in convective rain. In other words, there is no clear trend in all of these studies and the question is still opened. To explain these results somewhat contradictory, Ulbrich and Atlas [22] highlighted two types of sources of variability that contribute to the difficulty of making a clear distinction between the raindrop size distribution (DSD) and the associated Z-R relations in convective and stratiform precipitation. The first source of errors is related to the method of dis- crimination used for classification of the type of rain. The second source is the natural variability of the drops size which prevails within each type of rain. Tenorio et al. [26] , based on a dataset of raindrop size distribution collected in a coastal site of the State of Alagoas and in the north of Brazil, have noted that the continental and maritime DSD and consequently the Z-R relations showed significant differences. Unfortunately, they did not analyze the possible difference that might exist between a stratiform (or convective) rain type of marine origin and that of the same nature from continental origin.
In a recent study, Ochou et al. [17] have conducted the same investigations by using historical data of DSD gathered by the aid of a JW disdrometer type at four sites in West Africa (Abidjan, Boyele, Niamey and Dakar). Their work has been made at the rainy event scale with a large sample of 412 events including various types (squall lines, thunderstorms and stratiform rain). They showed the existence of three cases noted C1 (Ac < As and bc < bs), C2 (Ac < As and bc > bs) and C3 (Ac > As and bc < bs) from a given squall line to another (the letters c and s in index indicate respectively the convective or stratiform nature of rainfall). Their results revealed the coexistence of the above mentioned two schools, allowing finding the results from Yuter and Houze [21] through the case C3 as well as those of Tokay and Short [20] and T. Islam et al. [7] through the cases C1 and C2. Therefore, they have considered that the difference between the two schools could be explained by the fact that the microphysical conditions, responsible for the rainfall production, were different.
Based on the theoretical expression of Z and R as the statistical moments of order 6 (M6) and order 3.67 (M3.67) respectively and the results from Heinrich et al. [27] , Steiner et al. [28] and Lee and Zawadzki [24] justifying the influence of DSD through the size and number of raindrops on the Z-R relationships, Ochou et al. [17] used the ratio D0/NT of the median volumic diameter (D0) and the total number of drops per unit of volume (NT) to better understand the variability of the Z-R relationship in the rainy events, without assuming any analytical model (exponential, gamma or lognormal) of the DSD. Their approach was to establish a functional relationship between the ratio D0/NT and the rain rate at ground R, i.e. D0/NT = αRβ, similar to the relationship Z = ARb. From a comparative study, they determined a consistent behavior between the multiplicative factors A and α on the one hand and the exponents b and β on the other hand. Using the data collected in various sites in West Africa (Guinean and Sahelian zones) and from Central Africa (equatorial zone), and then grouped according to rain types (convective, stratiform and mixed), Ochou et al. [17] found the mean relations such as A = 2235.50.499 and b = 0.43β + 1.49, qualified as independent from the rainy event type and the climatic zone in spite of the high inherent Z-R relations variability. This result showed thus the consistency of the spatial and temporal variability of the Z-R relationship which can be justified by the microphysical processes involved in the precipitation formation.
In addition, several works, from satellite measurement [30] or from a network of pluviographs at the ground [31] have noted different types of precipitating systems from one climatic zone to another in Africa. This probably involves a variability according to their nature or following the efficiency of microphysical processes, which controls the rain formation. The dependence of DSD variability to climatological scales, daily, intra-daily, to physical processes or intra-process and its effects on the estimation of the rain rate R from the radar reflectivity Z has been explored in terms of bias and random errors by Lee and Zawadzki [24] . They have shown that the essential of DSD variability gets its origin within the rainy system or from a precipitating system to another in the same day. Based on a classification of physical processes leading to the formation of DSD from the vertical structure of data collected by a UHF radar collocated with the disdrometer, these authors showed that DSD variability between different physical processes is greater than the daily variability. Furthermore, the variability in the Z-R relation could derive from uncertainties in DSD measuring instruments. Campos and Zawadzki [31] , based on the comparisons of data from three types of collocated disdrometer (JW, OSP and POSS), stressed the instrumental dependence of Z-R relationship coefficients. They noted that the Z-R relationships from the three sensors exhibited differences comparable to those observed in distinct climate regions. Checa-Garcia et al. [32] , analyzed the binning effects on DSD measured by different coincident instruments including Joss-Waldvogel disdrometer (JW), Precipitation Occurrence Sensor System (POSS), Thies disdrometer, Parsivel OTT disdrometer, two-dimensional video disdrometer (2DVD) and optical spectro-pluviometer (OSP). They showed noticeable differences between instruments regarding to drop concentration, mean diameter, and other DSD parameters which were attributed to binning. In Africa where we have a diversity of precipitating systems, it is reasonable to wonder if the instruments are sufficiently stable so that observed variability from one system to another can be attributed to intrinsic characteristics of rainy events and not to the differences between the instruments or the collapse of their performance.
We propose in this work to analyze the coherence of the variability of the Z-R relationship, taking into ac- count the climatic conditions in which the rainy systems in Africa occurred and the types of instruments used for the measurement of raindrop size distributions. The present study has for main goal to examine the results obtained by Ochou et al. [17] with the help of the acquired database by the disdrometer JW in guinean, sahelian and equatorial Africa as well as in equatorial Latin America by comparing them to those obtained from data collected by the optical spectro-pluviometer (OSP) in Africa Soudan zone during the international campaign AMMA (African Monsoon Multidisciplinary Analyzes).
To achieve the assigned objectives, Section 2 is devoted to a description of the different types of disdrometer, the associated data as well as a brief overview of the observation sites. Section 3 is committed to the presentation of results relating to the consistent character of the Z-R relationships variability obtained from the disdrometer JW and OSP measurements, considering different types of precipitating systems and different climate zones; the discussion of these results is also conducted. Section 4 summarizes the whole results obtained.
2. Experimental Devices, Observation Sites and Database
The disdrometers constitute good tool mostly used for the measurement of DSD in the world. This paper used the data from Joss-Waldvogel (JW) disdrometer [33] [34] and the optical spectro-pluviometer (OSP), both hav- ing different technologies.
The widely used instrument for DSD measurement is the JW disdrometer. Its operating principle is based on the mechanical impact of drops. The data acquisition and processing chain was developed by Campistron et al. [35] . The measurement principle is such that the drops of rain, received every minute on the sampling area of the sensor (50 cm2), are classified according to the magnitude of their impacts in 25 channels covering the range of diameters between 0.3 and 5.2 mm by constant interval of 0.2 mm. For the collection of the data used in this work, JW disdrometer has been installed on five sites including four in Africa (Figure 1) and one pilot site in South America (Kourou, French Guyana). These sites are representative of different climatic zones (coastal equatorial: Abidjan and Kourou; Equatorial continental: Boyele; Sahelian coastal: Dakar; Sahelian continental: Niamey) and are swept away by different types of precipitating systems (thunderstorms, squall lines, stratiform rain). During these individual measurement campaigns, done at different periods listed in Table 1, 459 rainy events were sampled, providing 55,621 spectra representing a cumulative rain of 4982 mm.
The optical disdrometer OSP was installed during the intensive observation campaigns of the international program of African Monsoon Multidisciplinary Analyzes, AMMA [16] [36] , at the main site of Djougou in Benin as shown in Figure 1 and the secondary sites of Copargo and Nangatchiori (Table 1) located at around 20
Figure 1. Geographical location of disdrometer data collection sites and view of different operating instruments.
Table 1. Optical disdrometer (Parsivel, OSP, DBS) and JW disdrometer data sets used in this paper.
and 10 km, respectively, from the main site. The climate in this area is sudanian. The data were collected be- tween August 2005 and October 2007. However, for technical reasons, these disdrometers have not simultaneously operated during the rainy seasons. Unlike JW disdrometer, OSP is based on one of the optical properties of the drop of rain such as its attenuation capacity of a light beam [37] [38] . Two kinds of optical spectro-plu- viometer have been used for DSD data measurement: A single infrared beam and a double infrared beams dis- drometer (Figure 1). The attenuation induced by a raindrop on a light beam allows determining the integration time of the drop, the equivalent diameter of the drop as well as its vertical velocity [37] - [39] . For individual 1- min observations, the number of drops measured is stored in 32 classes of equivalent diameters between 0.0625 and 26 mm by increasing interval of 0.125 to 3 mm. The 32 classes of speeds are included between 0.05 and 20.80 m/s, by increasing interval of 0.1 to 3.2 m/s. It should be noted that because of the surface tension, the maximum diameter considered in fact for the raindrops is 6.2 mm. Sampling surfaces of the optical instruments are of 48.6 cm2 for the Parsivel model and 100 cm2 for the other two: OSP 01-02 and DBS 01 [16] [40] . The characteristics of the instruments, the coordinates of disdrometer location, the periods of operation, as well as the database are listed in Table 1. During the measurement periods, 93 rainy events were sampled, corresponding to a total of 11,647 1-min spectra of and a cumulative rain of 1220 mm. In addition, the site located in the North of Benin, are characterized by a majority of convective systems consisting of isolated thunderstorms and squall lines [16] [41] . Another important point to note is that the DSD measurements from disdrometers (JW and OSP) are always affected by errors and omissions [2] [5] [7] [13] [16] [20] [31] [40] [42] . However, the same authors have shown that these irregularities affect less the quality of observations.
In this work, we distinguished the spectra associated with convective and stratiform rain of squall lines based on the hyetogram by adopting the technique proposed by Testud et al. [43] . This approach is to classify a spectrum k as stratiform type if and only if its rain rate Rk and that of these twenty adjacent spectra (i.e. R10−k to R10+k) are all below 10 mmh−1. Otherwise, this spectrum k is convective type. Accordingly, when the spectrum k class is convective, its adjacent spectra are also. This method has been applied with success on several rainy events observed in tropical Africa in very recent studies conducted by Moumouni et al. [16] and Ochou et al. [17] .
3. Consistent Character of Z-R Relation Variability
It is instructive to dwell on the results of Ochou et al. [17] particularly on what they called quasi-constant functional relations A-α and b-β regardless to precipitation type and to assign this behavior to the consistent character of Z-R relations variability. This exercise remains the main objective to achieve in the development of this paper. Thus, to analyze the “coherent” character of the so-called results, we pointed out their approach described above in the introduction to this paper. First of all, this method is applied on the data obtained using other types of modern instruments of DSD measurement that are the optical spectro-pluviometers (OSP) whose different types was addressed in the section on the database. The results of our operation performed on the sampled rainy events registered during the AMMA campaigns at North Benin are confined in Table 2 and compared to those obtained by Ochou et al. [17] . To do this, the determination of relations was achieved by considering a single sample of rainy events according to their nature (whole squall lines, their convective or stratiform component, and thunderstorms) and the instrument (JWD or OSP) which has served to their acquisition.
The pre-factors and exponents of A-α and b-β relationships analysis reveals their quasi-similar character despite the large difference in the Z-R relationships derived from the formed samples and by considering the multiplicity of size and number of drops (D0, NT) combinations for a same type of rainy system, or from one type of
Table 2. Coefficients of the relationships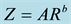 ,
, 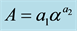 and
and  for two kinds of data for Ochou et al. (2011) and OSP data for the present study results.
for two kinds of data for Ochou et al. (2011) and OSP data for the present study results.
system to another as shown in Figure 2 and Figure 3. These latest figures show how the observed rainfall in various localities behaves during the different phases of squall lines and thunderstorms in the generated space of the D0 and NT parameters. We note various scenarios with rainfall controlled by variations only in the size of the drops, variations in the number of the drops or the combination of the two, regardless the precipitation nature or the type of precipitating system considered. Two considered types of precipitation could be characterized by close Z-R relations, but with a combination (D0, NT) different or with different Z-R relations and similar (D0, NT) combinations. However, taking into account simultaneously drops size and concentration in rain through the D0/NT ratio, allows us to identify the effect of drastic changes in the drop size distribution on the coefficients of Z-R relationship. These results from the OSP disdrometers are in agreement with those found by Ochou et al.
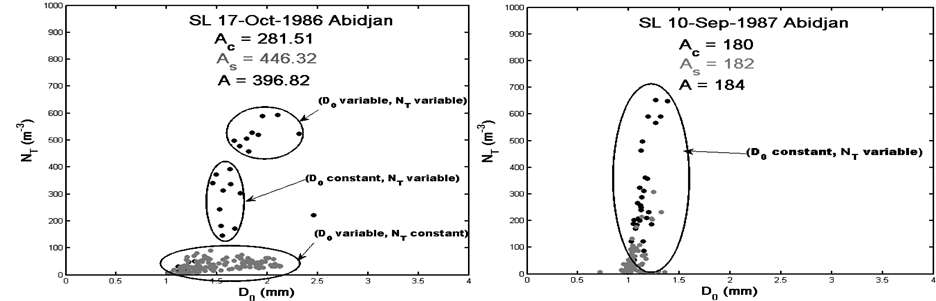
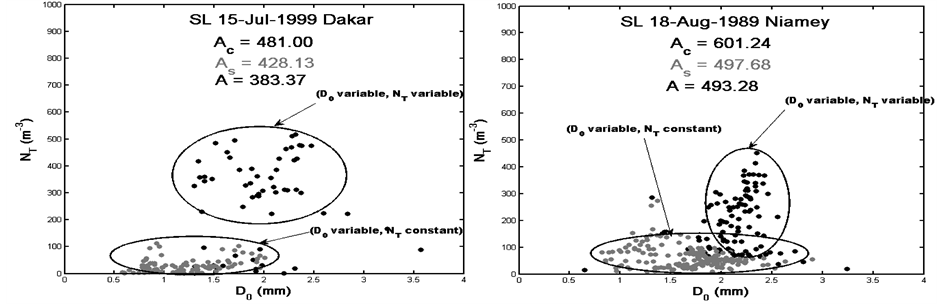
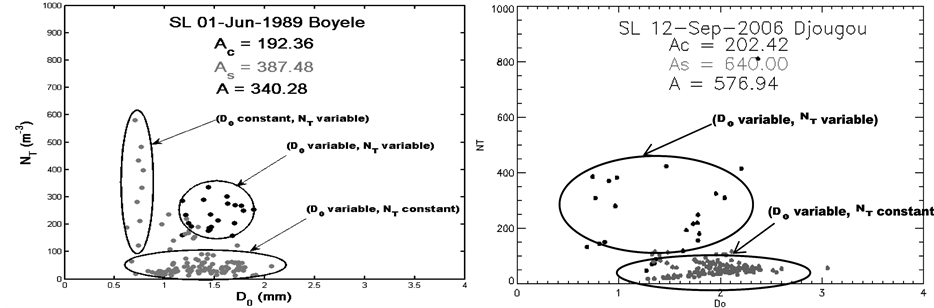
Figure 2. Variability of the raindrop size distribution and the pre-factor of Z-R relationship between squall lines observed at different sites, as reflected by the drop size D0 and drop number density NT.

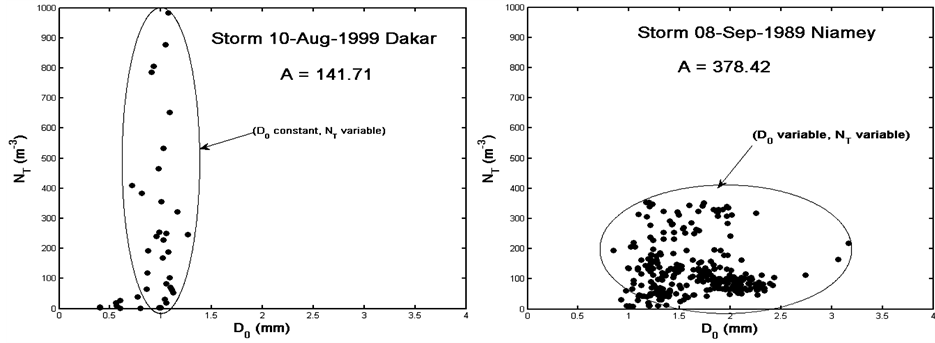
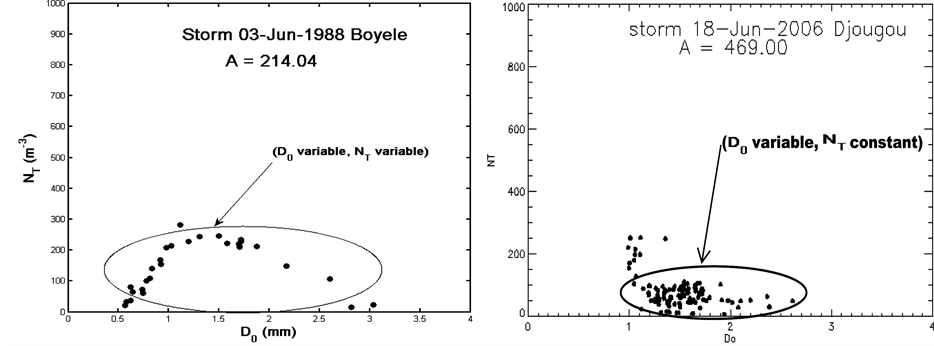
Figure 3. Same as in Figure 2 but for DSD collected during thunderstorms events.
[17] for the same types of precipitating systems. In other words, our functional relationships A-α and b-β ob- tained using DSD dataset recently acquired with OSP disdrometers, are similar to those of Ochou et al. [17] obtained from DSD data with mechanical impact JW disdrometer. The coefficients of variation of the parameters a1, a2, b1 and b2 are very close to those calculated by Ochou et al. [17] that are below 15%. The differences, al- though low, observed between the A-α and b-β relations obtained from OSP data and those relating to JW data whatever the sample rainy event, might be explained by the difference of the measuring channels in the two instrument technologies used. Indeed, the JW disdrometer do not detect the small drops of diameter less than 0.3 mm whereas for the optical spectro-pluviometer OSP, used at North Benin sites, a minimum threshold in diameter for spectrum sample is of 0.0625 mm. However, such similar results obtained with disdrometers based on very different technologies confirm the consistency of the functional relations A-α and b-β as pointed out by Ochou et al. [17] in their work. Steiner et al. [28] , from theoretical DSD, although having highlighted three specific modes that can explain the variability of the relationship Z-R, have noted that most of the rainy events show a variability of drop size distributions marked by a composition of simultaneous variations in drops size and number. They also concluded that taking into account joint fluctuations of these two parameters allowed the wide variability of relations Z-R to be understood. Despite the different uncertainties related to the sampling method and the data chain processing of JW and OSP disdrometers, reliable and consistent information on the microstructure of precipitating systems and mode of variability of the Z-R relationship could be obtained from the combination of drops size and number while the latter relationship is highly dependent on the type of instrument used [31] .
Such a result suggests that the microphysical processes responsible for the rainfall production (therefore of the distribution in size and in the number of raindrops) are well observed in the same way through the relations A-α and b-β and this, regardless the measuring instrument. Their knowledge would therefore be the key to better interpret the Z-R relationship variability within the precipitating systems.
In addition, the site of Djougou, characterized by a Sudan climate, differs, in a climatic point of view, from the other experimental sites (Abidjan: Coastal equatorial site; Boyele: Continental equatorial site; Dakar: Coastal Sahelian site; and Niamey: Continental Sahelian site) whose data were used in the work of Ochou et al. [17] . Using the regional differences in terms of climate (rainfall and temperature) highlighted by the works of Janicot [44] , Nicholson et al. [45] and Djomou et al. [46] , we plan to study the spatial variability of functional A-α and b-β relationships. Thus, we take advantage of the fact that DSD measurement sites are representative of different types of climates as mentioned above. Figure 4 shows the scatterplots of couples (A, α) and (b, β) as well as the fitting curves and corresponding related relations for Djougou, Abidjan, Boyele, Dakar and Niamey sites. The dataset selected for each site is composed of all gathered rainfall events presented in Table 1.
As can be seen from the graphs, the corresponding shapes of fitting relationships to A-α and b-β curves are identical to those found by Ochou et al. [17] and that, for all study sites. In other words, the multiplicative factor A and the exponent b of the Z-R relationship are well linked with α and β respectively. These results are confirmed by what appears considering rainy events observed in Kourou, located in South America where the dynamics of precipitating systems differs from that of the convective systems in West Africa. The correlation coefficients, higher than 0.80, denote well of the good relationship between the various parameters (A-α on one hand and b-β on the other hand). The set of coefficients for sampled types of rainy events from A-α and b-β at each site are in Table 3.
The analysis of these values clearly shows two categories of A-α and b-β relationships in Africa. Comparing the magnitudes of the coefficients of the functional relationships highlights two main regions. The first zone, called hereafter GI, covers Equatorial Coastal (Abidjan), Equatorial Continental (Boyele) and Sudan (Djougou) regions, i.e. it includes several types of climates (Guinean, equatorial, and Sudanian climate) and therefore several systems having different dynamics. Equations (1) to (3) below derived from the whole rainy events sampled at each site show similar results for these three types of climate forming the GI area.
Djougou:  and
and 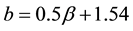 (1)
(1)
Abidjan: 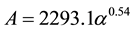 and
and  (2)
(2)
Boyele: 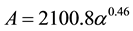
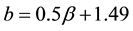
For the samples related to types of precipitating systems (squall lines, thunderstorms or stratiform events) in these three regions, we still observe values relatively close. Also, the relative differences in prefactors and ex- ponents a1, a2, b1 and b2 relative to the unique relationship established by Ochou et al. [17] based on gathered DSD measurements in Africa and less-homogeneous rain events (climate point of view) are less than 15% and confirm the stability of these relations in the GI area. Those derived from Kourou site located in South America equatorial region, following the different sampled rainy events (Table 3), exhibit the results of Abidjan, Boyele and Djougou observing sites. Thus, the stability of relations A-α and b-β and therefore the consistency of Z-R
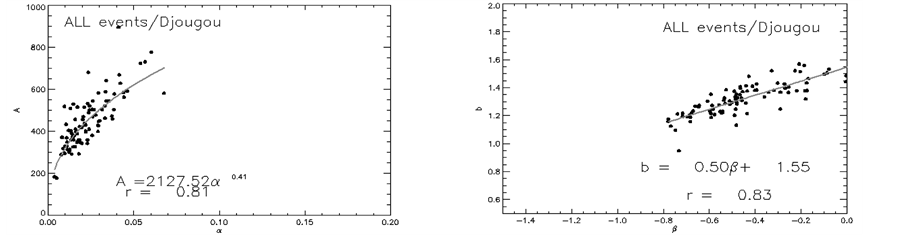

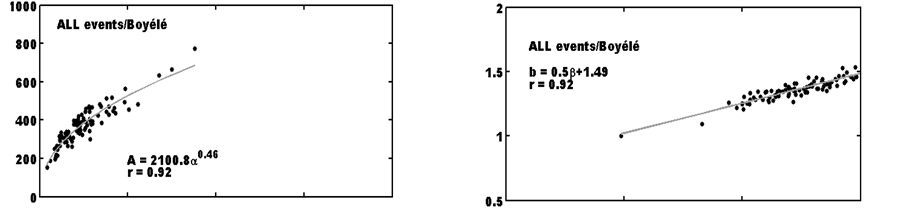
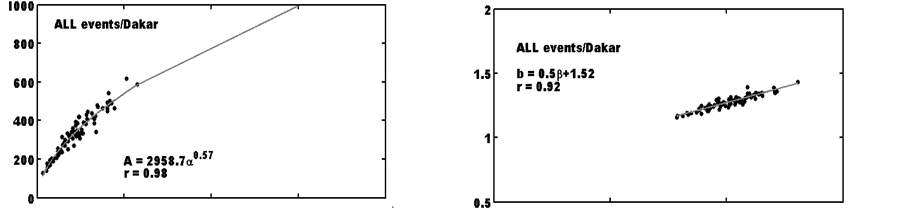
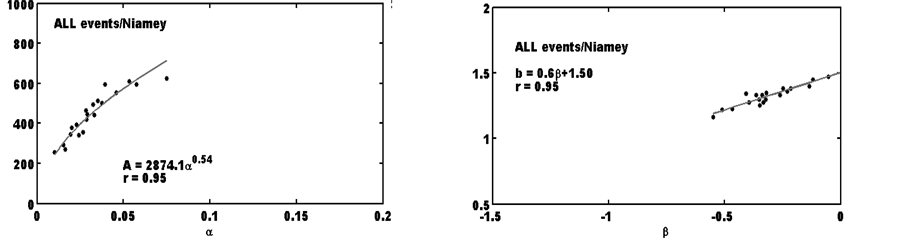
Figure 4. Relationship between the Z-R coefficients (A, b) and D0/NT-R coefficients (α, β) considering all the observed events, for different climate zones in Africa: Djougou (a) (b); Abidjan (c) (d); Boyele (e) (f); Dakar (g) (h); and Niamey (i) (j).
Table 3. Coefficients of the relationships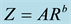
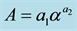
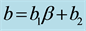
relationship variability through the simultaneously combination of raindrop size and number are confirmed.
The second area, noted GII hereafter, includes the coastal (Dakar) and continental (Niamey) sites located in Sahelian climate. In this area, the coincidence of the results with those of other sites is not obvious. The relations (4) and (5), based on the set of all rainy events of each site of this area, are significantly different from those found by Ochou et al. [17] . By comparing with GI, the relative differences exceeding the 30% regarding the pre- factors of A-α relationship give an idea of the significance of the coefficients behavior in GI to GII areas, while b-β relationship is relatively stable in these two areas.
Dakar: 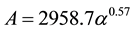
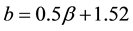
Niamey: 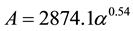
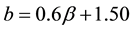
Several reasons could explain the observed differences in functional A-α relationship between GI and GII areas. A plausible reason for differences between these two zones would be the fact that the precipitating systems are different because of the wet or dry environments in which they develop, the samples homogeneity of rainy events considered. Indeed, in Sahelian zone (GII), Mathon and Laurent [29] and Mathon et al. [47] , by comparing the frequency distribution of the rainy events, observed from rainfall recorded by a 30 rain gauges network over 1990-1994 and 1996-1999 in the Sahel and based on the results of satellite tracking, have shown that almost 85% of precipitation produced to soil are related to organized convection systems (OCS). They have also shown that, using satellite imagery, the well-organized convective systems are less frequent and their average propagation speed is lower in the latitudes below the Sahelian zone while indicating that these parameters are decreasing up to the Guinean coast. More recent results by Depraetere et al. [30] , laying on a classification of precipitating systems from the ground based network AMMA-CATCH of rain gauges (located in GI zone), have shown a variety of rainy events with a smaller proportion (55%) compared to the Sahelian zone (equivalent to our area GII) of organized systems spreading with a well-defined speed. They have highlighted, from 700 major events observed from 1999 to 2006, three categories of precipitating systems, namely, 1) the category of systems having the typical signature of organized systems spreading with a well-defined speed, 2) the group of rainy systems called “ambiguous” likely coming from a combination of a system spreading and superimposed on another localized system, finally 3) the category of events having an uneven appearance without obvious spread, which could be associated with the local convection rather than to organized spreading systems. Therefore, we could reasonably assume that the homogeneous characters of sampled rainy events in Dakar and Niamey sites and heterogeneous ones in GI stations would explain the noted differences between these areas in terms of A-α relationship. These results by climate zone would show that the dynamic, certainly the clouds rainfall efficiency and therefore the microphysical processes leading to the formation of DSDs within the precipitating systems would vary from one area to the other.
However, the analysis of relations observing site by site (Table 3), for a considered type of system (e.g. thun- derstorms or squall lines), clearly shows a persistence of the differences between the A-α relationship of humid areas GI and Sahelian GII. This result reveals that the assumption of the homogeneity of sampled rainy events would explain such discrepancies with difficulty. In addition, the sites of the GI area representative of several types of climate (even if all these climates are humid) give close A-α and b-β relations. Similarly, the assumption for the involvement of microphysical process could be used to explain the differences between GI and GII areas knowing that the resulting combinations of parameters D0 and NT are different for a same type of systems (Figure 2 and Figure 3). But, such processes are already taken into account through the resulting ratio D0/NT.
From the foregoing explanations, another plausible reason for differences between GI and GII zones, in terms of A-α relationship, could derive from the fact that the precipitation, usually convective (Thunderstorms and squall lines) in the GII area (in West Africa), are often associated with aerosol clouds (dust and particles of sand). The work of McCollum et al. [48] , Perez et al. [49] have highlighted the fact that the desert region of Sahara and the semi-arid Sahel region are the main potential sources of sand and dust in west Africa. According to Foamouhoue et al. [50] , the storms of sand or dust are generally the result of convection movements in the atmosphere which is formed when the hot, lighter air particles arise and that the cold, heavier air particles come down to take its place. These large quantities of sand and dust can be transported over thousands of kilometers by convection currents, which could cause a mix of rain and sand/dust in this area GII. It is not the scope of this paper to study the processes related to the desert dust nor their implications in West Africa monsoon which governs the rainfall. But, we draw attention to the fact that such storms of mixed particles could be, for the JW disdrometer, sources of additional acoustic noise due to the impacts of the particles of sand and dust that could be superimposed on those products by the rain itself [51] . Thus, from a sampling spectra by the JW impact disdrometer having an electromechanical technology, as it was the case in Dakar and Niamey sites located within the sources zones of sand and dust storms, false spurious spectra (mixture of raindrops and sand/dust particles) would therefore be likely to contaminate the sampled DSDs. Indeed, such an instrument suffers from difficulties to distinguish raindrops and the particles of sand/dust which would fall simultaneously or almost simultaneously [51] . Unfortunately, we could not eliminate such spectra. From this, the variability of A-α relationships from one area to another seems logical because it has been revealed in the literature that instrumental limitations mainly affect the coefficient A of the Z-R relation [28] [52] - [55] . Steiner et al. [28] have also shown that difficulties, encountered in the microphysical interpretation of the Z-R relation factor A variability, come also from instru- mental limitations. Such situation, affecting mainly the factor A, would therefore explain the quasi-similar b-β relationships observed from one climate zone to another.
In contrast, within each of the two zones (GI and GII), we note the similarity of A-α and b-β relations. This demonstrates the consistency of Z-R relationship variability which is well catched through the D0/NT ratio. However, the similarity of the GI area relations with those obtained by Ochou et al. [17] can be explained by the fact that the rainy events (and therefore the DSD) observed at these sites (Abidjan and Boyele) are most numerous compared to those from the sahelian sites (area GII), so that by pooling of data from both areas conducted by Ochou et al. [17] , the dominance, which is justified from a statistical point of view, has gone to the coeffi- cients of the GI area.
4. Conclusions
Two types of disdrometer based on different measuring principles and installed in various sites in Africa (Abidjan, Boyele, Dakar, Niamey, Djougou) and in French Guyana (Kourou) are compared: electromechanical JW disdrometers operated in Abidjan, Boyele, Dakar, Niamey, Kourou and optical spectro-pluviometers installed in North Benin at Djougou. The large samples of measured DSDs for more than five hundred (500) rainy events are used here to assess the consistency of the Z-R relationship variability. Although these instruments are not collocated, the diversity and the significant number of rainy events is an important asset to better identify the physical (therefore natural) or instrumental origin in the variability of this relationship. An important task was to determine whether the different types of disdrometer react in the same manner for the different types of precipi- tation.
We confirm clearly that the relationship Z-R is characterized by a high spatial variability, from a type of pre- cipitation to another and within the same precipitation (case of squall lines) and, regardless of the type of dis- drometer used for measuring the DSD. For example, by considering our sample of squall lines observed in North Benin from an OSP disdrometer , the Z-R relationship obtained in the convective part is Z = 290R1.43, while in the stratiform part, we get Z = 562R1.44. For the sample of squall lines used in the work of Ochou et al. [17] , the relations Z-R corresponding to the convective and stratiform rainfall are respectively Z = 302R1.33 and Z = 427R1.34.
This work illustrates that, in spite of A and b coefficients high variability (and therefore the Z-R relationship variability) from a type of precipitation to another, within the same type of system and, from one climate zone to another (Table 3), the A-α and b-β functional relationships designed to understand the involvement of the para- meters D0 and NT of DSD in the variability of Z-R relation are consistent. This clearly reflects that, the variability of the coefficients A and b would be mainly in the joint variation of the raindrops size and number, regardless the type of disdrometer used and their instrumental uncertainties.
While Ochou et al. [17] , indicated a quasi-constant relation by using all available DSD data gathered from all the sites, two main categories of A-α and b-β relationships emerge from this study. Spatial (humid and sahelian regions) variation of these relations is exhibited. It was suggested that these differences could be due to spurious spectra interference coming from winds of sand and dust which may affect the quality of the data in the sahelian region sites where impact JW disdrometers have operated. So, it was useful to note that any Z-R variability from DSD should indicate information on location and type of disdrometer. Thus, it will be possible to separate in- strumental and physical variations in Z-R relationship.
In future studies, an obvious issue would be to study the microphysical origins of Z-R relationship variability. To do this, we could, from vertical pointing Micro Rain Radar measurements collected in North Benin during the AMMA campaign, address the issue of microphysical processes efficiency and their impact on Z-R relationship given different precipitating systems. Similarly, it appears to us interesting to see how the intrinsic rainfall microstructure characteristics that are raindrop size and number, resulting from the microphysical processes, evolve within a season and from one season to another in relation with other climatic parameters of interest such as the sea surface temperature (SST) and the trace at ground of the intertropical convergence zone (FIT).
Acknowledgements
Based on a French initiative, AMMA was built by an international scientific group and is currently funded by a large number of agencies, especially from France, UK, US and Africa. It has been the beneficiary of a major fi- nancial contribution from the European Community’s Sixth Framework Research Program. Detailed informa- tion on scientific coordination and funding is available on the AMMA International web site http://www.amma-international.org.
The authors are also grateful to all of those who contributed to the collecting of JWD data used in this study, under the lead of Prof. Henri Sauvageot from the Atmospheric Research Center (Toulouse, France).
Financial support for this paper has been provided by PARRAF of AIRD under the RHYVA Project.
References
- Marshall, J.S. and Palmer, W.M.K. (1948) The Distribution of Raindrops with Size. Journal of Meteorology, 5, 165-166. http://dx.doi.org/10.1175/1520-0469(1948)005<0165:TDORWS>2.0.CO;2
- Sauvageot, H. and Lacaux, J.P. (1995) The Shape of Averaged Drop Size Distributions. The Journal of the Atmos- pheric Sciences, 52, 1070-1083. http://dx.doi.org/10.1175/1520-0469(1995)052<1070:TSOADS>2.0.CO;2
- Ochou, A.D., Koffi, M. and Sauvageot, H. (1999) Climatologie des distributions des gouttes de pluie en zone côtière ivoirienne. Publications de l’Association Internationale de climatologie, 12, 252-260.
- Rosenfeld, D. and Ulbrich, C.W. (2003) Cloud Microphysical Properties, Processes, and Rainfall Estimation Opportunities. Radar and Atmospheric Science: A Collection of Essays in Honor of David Atlas. Meteorological Monographs, 30, 237-258.
- Nzeukou, A., Sauvageot, H., Ochou, A.D. and Kebe, C.M.F. (2004) Raindrop Size Distribution and Radar Parameters at Cape Verde. J. Appl. Meteor., 43, 90-105.
- Kozu, K., Reddy, K., Mori, S., Thurai, M., Ong, J.T., Rao, D.N. and Shimomai, T. (2006) Seasonal and Diurnal Variations of Raindrop Size Distribution in Asian Monsoon Region. Meteorological Society of Japan, 84, 195-209. http://dx.doi.org/10.2151/jmsj.84A.195
- Islam, T., Rico-Ramirez, A.M., Thurai, M. and Han, D. (2012) Characteristics of Raindrop Spectra as Normalized Gamma Distribution from a Joss-Waldvogel Disdrometer. Atmospheric Research, 108, 57-73. http://dx.doi.org/10.1016/j.atmosres.2012.01.013
- Marshall, J.S. (1969) Power-Law Relations in Radar Meteorology. Journal of Meteorology, 5, 165-166. http://dx.doi.org/10.1175/1520-0469(1948)005<0165:TDORWS>2.0.CO;2
- Battan, L.J. (1973) Radar Observation of the Atmosphere. University of Chicago Press, Chicago, 323 p.
- Wilson, J.W. and Brandes, A.E. (1979) Radar Measurement of Rainfall―A Summary. Bulletin of the American Meteorological Society, 60, 1048-1058. http://dx.doi.org/10.1175/1520-0477(1979)060<1048:RMORS>2.0.CO;2
- Austin, P.M. (1987) Relation between Measured Radar Reflectivity and Surface Rainfall. Monthly Weather Review, 115, 1053-1070.
- Uijlenhoet, R. (2001) Raindrop Size Distributions and Radar Reflectivity―Rain Rate Relationships for Radar Hydrology. Hydrology and Earth System Sciences, 5, 615-627.
- Ochou, A.D., Nzeukou, A. and Sauvageot, H. (2007) Parametrization of Drop Size Distribution with Rain Rate. Atmospheric Research, 84, 58-66.
- Atlas, D., Ulbrich, C.W., Marks Jr., F.D., Amitai, E. and Williams, C.R. (1999) Systematic Variation of Drop Size and Radar-Rainfall Relations. Journal of Geophysical Research, 104, 6155-6169.
- Maki, M., Keenam, T.D., Sasaki, Y. and Nakamura, K. (2001) Characteristics of the Raindrop Size Distribution in Con- tinental Tropical Squall Lines Observed in Darwin, Australia. Journal of Applied Meteorology, 40, 1393-1412.
- Moumouni, S., Gosset, M. and Houngninou, E. (2008) Main Features of Rain Drop Size Distributions Observed in Benin, West Africa, with Optical Disdrometers. Geophysical Research Letters, 35, Article ID: L23807. http://dx.doi.org/10.1029/2008GL035755
- Ochou, A.D., Zahiri, E.P., Bamba, B. and Koffi, M. (2011) Understanding the Variability of Z-R Relationships Caused by Natural Variations in Raindrop Size Distributions (DSD): Implication of Drop Size and Number. Atmospheric and Climate Sciences, 1, 147-164. http://dx.doi.org/10.4236/acs.2011.13017
- Waldvogel, A. (1974) The N0 Jump in Raindrop Spectra. Journal of the Atmospheric Sciences, 31, 1067-1078. http://dx.doi.org/10.1175/1520-0469(1974)031<1067:TJORS>2.0.CO;2
- Balakrishnan, N., Zrnic, D.S., Goldhirsh, J. and Rowland, J. (1989) Comparison of Simulated Rain Rate from Disdrometer Data Employing Polarimetric Radar Algorithms. Journal of Atmospheric and Oceanic Technology, 6, 476-486. http://dx.doi.org/10.1175/1520-0426(1989)006<0476:COSRRF>2.0.CO;2
- Tokay, A. and Short, D.A. (1996) Evidence from Tropical Raindrop Spectra of the Origin of Rain from Stratiform versus Convective Clouds. Journal of Applied Meteorology, 35, 355-371. http://dx.doi.org/10.1175/1520-0450(1996)035<0355:EFTRSO>2.0.CO;2
- Yuter, S.E. and Houze, R.A. (1997) Measurements of Raindrop Size Distribution over the Pacific Warm Pool and Implementations for Z-R Relations. Journal of Applied Meteorology, 36, 847-867. http://dx.doi.org/10.1175/1520-0450(1997)036<0847:MORSDO>2.0.CO;2
- Ulbrich, C.W. and Atlas, D. (2002) On the Separation of Tropical Convective and Stratiform Rains. Journal of Applied Meteorology, 41, 188-195. http://dx.doi.org/10.1175/1520-0450(2002)041<0188:OTSOTC>2.0.CO;2
- Uijlenhoet, R., Steiner, M. and Smith, J.A. (2003) Variability of Raindrop Size Distributions in a Squall Line and Implications for Radar Rainfall Estimation. Journal of Hydrometeorology, 4, 43-61. http://dx.doi.org/10.1175/1525-7541(2003)004<0043:VORSDI>2.0.CO;2
- Lee, G.W. and Zawadzki, I. (2005) Variability of Drop Size Distributions: Time-Scale Dependence of the Variability and Its Effects on Rain Estimate. Journal of Applied Meteorology, 44, 241-255. http://dx.doi.org/10.1175/JAM2183.1
- Narayana Rao, T., Narayana Rao, D. and Mohan, K. (2001) Classification of Tropical Precipitating Systems and Associated Z-R Relationships. Journal of Geophysical Research, 106D, 17699-17711.
- Tenorio, R.S., Moraes, M.C.S. and Sauvageot, H. (2012) Raindrop Size Distribution and Radar Parameters in Coastal Tropical Rain Systems of Northeastern Brazil. Journal of Applied Meteorology and Climatology, 51, 1960-1970. http://dx.doi.org/10.1175/JAMC-D-11-0121.1
- Huggel, A., Schmid, W. and Waldvogel, A. (1996) Raindrop Size Distributions and the Radar Bright Band. Journal of Applied Meteorology, 35, 1688-1701. http://dx.doi.org/10.1175/1520-0450(1996)035<1688:RSDATR>2.0.CO;2
- Steiner, M., Smith, J.A. and Uijlenhoet, R. (2004) A Microphysical Interpretation of Radar Reflectivity-Rain Rate Relationships. Journal of the Atmospheric Sciences, 61, 1114-1131. http://dx.doi.org/10.1175/1520-0469(2004)061<1114:AMIORR>2.0.CO;2
- Mathon, V. and Laurent, H. (2001) Life Cycle of the Sahelian Mesoscale Convective Cloud Systems. Quarterly Journal of the Royal Meteorological Society, 127, 377-406.
- Depraetere, C., Gosset, M., Ploix, S. and Laurent, H. (2009) The Organization and Kinematics of Tropical Rainfall Systems Ground Tracked at Mesoscale with Gages: First Results from the Campaigns 1999-2006 on the Upper Oueme Valley (Benin). Journal of Hydrology, 375, 143-160. http://dx.doi.org/10.1016/j.jhydrol.2009.01.011
- Campos, E. and Zawadzki, I. (2000) Instrumental Uncertainties in Z-R Relations. Journal of Applied Meteorology, 39, 1088-1102. http://dx.doi.org/10.1175/1520-0450(2000)039<1088:IUIZRR>2.0.CO;2
- Checa-Garcia, R., Tokay, A. and Tapiador, F.J. (2014) Binning Effects on in Situ Raindrop Size Distribution Measurements. Atmos. Meas. Tech. Discuss., 7, 2339-2379. http://dx.doi.org/10.5194/amtd-7-2339-2014
- Joss, J. and Waldvogel, A. (1967) Ein Spektrograph für Niederschlagstropfen mit automatischer Auswertung. Pure and Applied Geophysics, 68, 240-246. http://dx.doi.org/10.1007/BF00874898
- Joss, J. and Waldvogel, A. (1969) Raindrop Size Distribution and Sampling Size Errors. Journal of the Atmospheric Sciences, 26, 566-569. http://dx.doi.org/10.1175/1520-0469(1969)026<0566:RSDASS>2.0.CO;2
- Campistron, B., Despaux, G.R. and Lacaux, J.P. (1987) A Microcomputer Data-Acquisition System for Real-Time Processing and Raindrop Size Distribution Position with the RD-69 Disdrometer. Journal of Atmospheric and Oceanic Technology, 4, 536-540. http://dx.doi.org/10.1175/1520-0426(1987)004<0536:AMDASF>2.0.CO;2
- Redelsperger, J.L., Thorncroft, C., Diedhiou, A., Lebel, T., Parker, D. and Polcher, J. (2006) African Monsoon Multidisciplinary Analysis (AMMA): An International Research Project and Field Campaign. Bulletin of the American Meteorological Society, 88, 1739-1746. http://dx.doi.org/10.1175/BAMS-87-12-1739
- Salles, C., Creutin, J.D. and Sempere-Torres, D. (1998) The Optical Spectro-Pluviometer Revisited. Journal of Atmospheric and Oceanic Technology, 15, 1215-1222. http://dx.doi.org/10.1175/1520-0426(1998)015<1215:TOSR>2.0.CO;2
- Delahaye, J.Y., Barthes, L., Gole, P., Lavergnat, J. and Vinson, J.P. (2005) A Dual-Beam Spectro-Pluviometer Concept. Journal of Hydrology, 328, 110-120. http://dx.doi.org/10.1016/j.jhydrol.2005.11.048
- Lӧffler-Mang, M. and Joss, J. (2000) An Optical Disdrometer for Measuring Size and Velocity of Hydrometeors. Jour- nal of Atmospheric and Oceanic Technology, 17, 130-139.
- Chapon, B., Delrieu, G., Gosset, M. and Boudevillain, B. (2008) Variability of Rain Drop Size Distribution and Its Effect on the Z-R Relationship: A Case Study for Intense Mediterranean Rainfall. Atmospheric Research, 87, 52-65. http://dx.doi.org/10.1016/j.atmosres.2007.07.003
- Gosset, M., Zahiri, E.P. and Moumouni, S. (2010) Rain Drop Size Distribution Variability and Impact on X-Band Polarimetric Radar Retrieval: Results from the AMMA Campaign in Benin. Quarterly Journal of the Royal Meteorological Society, 136, 243-256. http://dx.doi.org/10.1002/qj.556
- Sheppard, B.E. and Joe, P.I. (1993) Comparison of Raindrop Size Distribution Measurements by a Joss-Waldvogel Disdrometer, a PMS 2DG Spectrometer, and a POSS Doppler Radar. Journal of Atmospheric and Oceanic Technology, 11, 874-887. http://dx.doi.org/10.1175/1520-0426(1994)011<0874:CORSDM>2.0.CO;2
- Testud, J., Oury, S., Black, R.A., Amayenc, P. and Dou, X.K. (2001) The Concept of Normalised Distribution to Describe Raindrop Spectra: A Tool for Cloud Physics and Cloud Remote Sensing. Journal of Applied Meteorology, 40, 1118-1140. http://dx.doi.org/10.1175/1520-0450(2001)040<1118:TCONDT>2.0.CO;2
- Janicot, S. (1992) Spatiotemporal Variability of West African Rainfall. Part I: Regionalization and Typings. Journal of Climate, 5, 489-497. http://dx.doi.org/10.1175/1520-0442(1992)005<0489:SVOWAR>2.0.CO;2
- Nicholson, S.E., Some, B. and Kone, B. (2000) An Analysis of Recent Rainfall Conditions in West Africa, Including the Rainy Seasons of the 1997 El Nino and the 1998 La Nina Years. Journal of Climate, 13, 2628-2640. http://dx.doi.org/10.1175/1520-0442(2000)013<2628:AAORRC>2.0.CO;2
- Djomou, Z.Y., Monkam, D. and Lenouo, A. (2009) Spatial Variability of Rainfall Regions in West Africa during the 20th Century. Atmospheric Science Letters, 10, 9-13. http://dx.doi.org/10.1002/asl.202
- Mathon, V., Laurent, H. and Lebel, T. (2002) Mesoscale Convective System Rainfall in the Sahel. Journal of Applied Meteorology, 41, 1081-1092. http://dx.doi.org/10.1175/1520-0450(2002)041<1081:MCSRIT>2.0.CO;2
- McCollum, J.R., Gruber, A. and Ba, M.B. (2000) Discrepancy between Gauges and Satellite Estimates of Rainfall in Equatorial Africa. Journal of Applied Meteorology, 39, 666-679. http://dx.doi.org/10.1175/1520-0450-39.5.666
- Perez, C.S., Nickovic, S., Baldasano, J.M., Sicard, M., Rocadenbosch, F. and Cachorro, V.E. (2006) A Long Saharan Dust Event over the Western Mediterranean: Lidar, Sun Photometer Observations, and Regional Dust Modeling. Journal of Geophysical Research, 111, Article ID: D15214. http://dx.doi.org/10.1029/2005JD006579
- Foamouhoue, A.K., Baldasano, J.M., Agulló, E.C., Diongue-Niang, A., García-Pando, C.P., Poolman, E. and Thomson, M. (2009) Activités de recherche-développement de l’OMM sur la qualité de l’air, le temps et le climat au profit de l’Afrique. WMO Bulletin, 58, 41-47.
- Caracciolo, C., Prodi, F. and Uijlenhoet, R. (2006) Comparison between Pludix and Impact/Optical Disdrometers during Rainfall Measurements Campaigns. Atmospheric Research, 82, 137-163. http://dx.doi.org/10.1016/j.atmosres.2005.09.007
- Ulbrich, C.W. (1983) Natural Variations in the Analytical Form of the Raindrop Size Distribution. Journal of Climate and Applied Meteorology, 22, 1764-1775. http://dx.doi.org/10.1175/1520-0450(1983)022<1764:NVITAF>2.0.CO;2
- Ulbrich, C.W. (1985) The Effects of Drop Size Distribution Truncation on Rainfall Integral Parameters and Empirical Relationships. Journal of Climate and Applied Meteorology, 24, 580-590. http://dx.doi.org/10.1175/1520-0450(1985)024<0580:TEODSD>2.0.CO;2
- Feingold, G. and Levin, Z. (1986) The Lognormal Fit to Raindrop Spectra from Frontal Convective Clouds in Israel. Journal of Climate and Applied Meteorology, 25, 1346-1363. http://dx.doi.org/10.1175/1520-0450(1986)025<1346:TLFTRS>2.0.CO;2
- Ulbrich, C.W. and Atlas, D. (1998) Rainfall Microphysics and Radar Properties: Analysis Methods for Drop Size Spectra. Journal of Applied Meteorology, 37, 912-923. http://dx.doi.org/10.1175/1520-0450(1998)037<0912:RMARPA>2.0.CO;2



