Advances in Chemical Engineering and Science
Vol. 2 No. 2 (2012) , Article ID: 18916 , 12 pages DOI:10.4236/aces.2012.22036
Comparison of Co-Current and Counter-Current Flow Fields on Extraction Performance in Micro-Channels
1Department of Mathematical Analysis, Ghent University, Ghent, Belgium
2Department of Chemical Engineering, Indian Institute of Technology Madras (IIT Madras), Chennai, India
Email: bm@cage.ugent.be, *spush@iitm.ac.in
Received December 12, 2011; revised January 24, 2012; accepted February 25, 2012
Keywords: Plug flow; Diffusion; Extraction; co-current; counter-current
ABSTRACT
Several applications such as liquid-liquid extraction in micro-fluidic devices are concerned with the flow of two immiscible liquid phases. The commonly observed flow regimes in these systems are slug-flow and stratified flow. The latter regime in micro-channels has the inherent advantage that separation of the two liquids at the exit is efficient. Recently extraction in a stratified counter-current flow has been studied experimentally and it has been shown to be more efficient than co-current flow. An analytical as well as a numerical method to determine the steady-state solution of the corresponding convection-diffusion equation for the two flow-fields is presented. It is shown that the counter-current process is superior to the co-current process for the same set of parameters and operating conditions. A simplified model is proposed to analyse the process when diffusion in the transverse direction is not rate limiting. Different approaches to determining mass transfer coefficient are compared. The concept of log mean temperature difference used in design of heat exchangers is extended to describe mass transfer in the system.
1. Introduction
The physical effects which govern the behavior of fluids flowing at the micro-scale and the macro-scale are different. Surface tension, viscous effects, energy dissipation and capillary action begin to dominate system behavior at the micro-scale. Micro-fluidics studies the behavior of the fluids at the micro-scale induced by these effects. It helps exploit the behavior at these scales for new applications by improving the efficiency of current processes.
Micro-fluidics results in Process Intensification through miniaturization. These systems are characterized by a dominance of viscous forces as compared to inertial forces; hence, typically low Reynolds numbers are encountered. Consequently, the flow regimes observed in these systems is laminar. Mixing in these micro-channels occurs primarily by molecular diffusion. The time needed for mixing by molecular diffusion is proportional to the square of the length of the diff usion path. The marked shortening of the diffusion path in a micro-channel results in relatively good mixing.
Multiphase liquid-liquid flows arise when two or more partially miscible or completely immiscible fluids are brought in contact and subjected to a pressure gradient. The resulting systems display different kinds of flow behavior, e.g. droplet, slug or stratified flow. These regimes depend on the relative flow rates of the fluid phases involved, the resulting interaction between interfacial and viscous forces and the wetting behavior of the channel walls. Different liquid-liquid two-phase flow patterns in micro-channels have been experimentally analysed, see Dessimoz et al. [1].
In the context of mass transfer across membranes Guo and Ho [2] have analysed an analytical solution based on separation of variables for co-current and counter-current flows in an annulus. The eigen-functions were obtained using a power series expansion. Here the velocity fields in the two chambers were decoupled as they were separated by a porous membrane. Electro-osmotic flows in micro channels have been frequently proposed as a way to overcome dispersion effects. This causes the velocity profile in the micro-channel to remain almost uniform except for a small region near the walls. The flow-field under these conditions can be approximated as an ideal plug-flow in the micro-channel. Liu et al. [3] and Gao et al. [4] have studied the electro-osmotic flow in a rectangular channel when one fluid is conducting and the other is non conducting as is usually the case in extraction. The flow-profiles were obtained analytically for the two fluids when the non conducting fluid was dragged by the viscous force of the conducting fluid. Wang et al. [5] have studied experimentally as well as theoretically how the interface level can be controlled in a two liquid system under the influence of a pressure drop and an electric field applied to one of the fluids. Their results indicate that the flow profiles in the two fluids can be approximated as plug-flows with a jump discontinuity at the interface for some operating conditions.
Recent studies have focused on liquid-liquid extraction in the stratified flow regime in the micro-channels. Here the two fluids flow side by side. This flow-pattern can be exploited to facilitate complete separation at the channel exit. The extraction of vanillin dissolved in water using toluene in micro-structured devices made of Poly Di Methyl Siloxane (PDMS) was studied experimentally by Fries et al. [6]. Here the performance of segmented and stratified flow regimes were compared. LIF and microPIV measurements showed a laminar profile for stratified flow, whereas vortices in the slug were detected for segmented flow. The influence of channel width and therefore, the surface-to-volume ratio was investigated for stratified flow. There was a significant enhancement of mass transfer with decrease in the channel cross-sectional area for the stratified flow regime.
Three different fluid-flow patterns in a Y-shaped micro-channel, contact or stratified flow, segmented flow and emulsification were investigated in Okubo et al. [7]. Here a one-dimensional model for extraction assuming the interface to be at the centre of the channel was used to compare the model predictions with the experimental behavior. A two-dimensional flow-field taking into account the effect of the interface not being at the centre was analysed numerically by Žnidaršič-Plazl and Igor Plazl [8]. They compare their model predictions with experimental results on steroid extraction. Most of the research in stratified flow has been when the fluids flow co-currently i.e. in the same direction. TeGrotenhuis et al. [9] has studied the counter-current mass transfer in a micro-channel when the two fluids are separated by a membrane. Here the diff usional resistance through the membrane was incorporated in the analysis. Recently it has been shown that by suitable modification of the channel surface it is possible to have counter-current flow in the micro-channels over a wide range of operating conditions, Aota et al. [10]. They found that a maximum possible theoretical plate number of 4.6 is achievable in counter-current flow as opposed to co-current flow. The pressure drop characteristics in a counter-flow micro-channel have been investigated by Hibara et al. [11]. The velocity profiles in a 100 micron channel with butylacetate and an aqueous phase flowing in a countercurrent manner was measured using micro-PIV, Aota et al. [12].
The counter-current flow is known to be more efficient in the context of heat exchanger networks. In this work the performance of co-current and counter-current flows in extraction is being studied with focus on micro-channels. Recently it has been experimentally shown that counter-current operation is possible in micro-channels. The primary objective of this work is to establish conditions under which the counter-current operation is superior to the co-current operation. To the best of our knowledge a theoretical analysis of this system has not been carried out. The main motivation is to show that improvements in the extraction performance are possible when the flow is counter-current as opposed to co-current. The convective diffusion equation is solved analytically for the co-current operation. This is a one dimensional model with diffusion being considered only in the direction transverse to the flow direction. Here axial dispersion effects are neglected. The counter-current system is solved numerically. The algorithm proposed exploits the features of the system. A lumped model is analysed where the concentration dependency on the flow direction alone is considered. It is shown that the counter-current flow performs better than the co-current flow. Different methods to compute the mass transfer coefficient as proposed in the literature are compared.
2. Co-Current and Counter-Current Flow
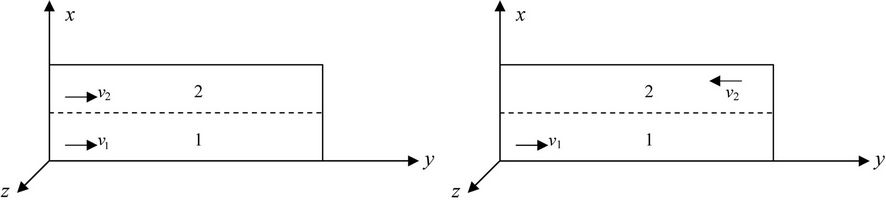
We consider three different flow regimes for the analysis in this work: 1) co-current laminar flow, 2) co-current plug flow, and 3) counter-current plug flow. The stratified flow (fluids flow side by side as shown in Figure 1) of two liquid phases is analysed between two infinite horizontal plates extending to infinity in the z-direction. This assumption on the geometry helps us focus on the physics of the problem keeping the mathematics tractable. The distance between the plates (along the x-direction) is taken as H and the liquid-liquid interface is at distance hl (subscript l for laminar) from the lower plate. The flow is assumed to be in the y-direction. Figure 1 shows a schematic of the system being analyzed.
2.1. Laminar Flow
In the case of laminar or Poiseuille flow, the velocity profile is obtained assuming the flow to be steady, fully developed and the liquids to be incompressible. The velocity profiles of the system are governed by the equations
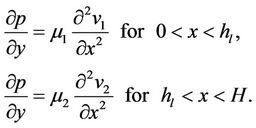 (1)
(1)
These equations are subject to the conditions of no slip at the walls and continuity of velocity and shear stress at
 (a) (b)
(a) (b)
Figure 1. Micro-channel layout. 1,2 describe regions occupied by the two fluids. These are separated at the interface h. The direction of velocity determines the flow type. (a) Co-current; (b) Counter-current.
the interface which is located at hl. So
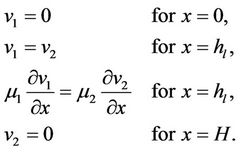 (2)
(2)
In the above the subscript 1 and 2 are used to denote the fluid in the first and second region respectively. The solutions to the above equation yield the velocity profiles of the two liquids as Equation (3).
Here the imposed pressure gradient is denoted as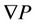 . Both the fluids are subject to the same pressure drop. The flow behavior is hence similar to the Hagen-Poiseuille flow (parabolic in shape). The velocity field is continuous at the interface hl but its derivatives are discontinuous. A schematic of the velocity profile in the channel is shown in Figure 2.
. Both the fluids are subject to the same pressure drop. The flow behavior is hence similar to the Hagen-Poiseuille flow (parabolic in shape). The velocity field is continuous at the interface hl but its derivatives are discontinuous. A schematic of the velocity profile in the channel is shown in Figure 2.
The experimentalist operates the system at fixed flowrates Q1 and Q2.
They are given by Equation (4).
These equations can be used to determine the pressure drop ∇P and the height h of the interface for a given combination of flow-rates and fluids. Alternatively, if the pressure drop and height of interface are specified, the velocity profiles in each liquid layer can be found and from this the flow rates can be determined.
2.2. Co-Current Plug Flow
In this case the velocities v1 and v2 have the same sign, and are constant within their phase. It is well established that plug flow behavior can be achieved in a micro channel using electro-osmosis [4]. This eliminates axial dispersion effects which arise from laminar flow in micro-channels. The electric field can also be used to control the interface height for a fixed combination of flowrates.
In the case of plug flow, with equal velocity in both phases, we denote interface as h = hn. Here
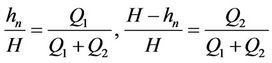
When plug flow is assumed viscosity does not play any role in determining the interface position. If on the other hand we assume the flow to be laminar, then the interface position is determined by the viscosity of the two fluids.
2.3. Counter-Current Plug Flow
In this case the velocities v1 and v2 have an opposite sign. We take 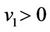 and
and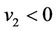 . Counter-current flow can be theoretically simulated using a combination of Poiseulle flow and a Couette flow. To generate a clear separation of the two phases the interface must be located at
. Counter-current flow can be theoretically simulated using a combination of Poiseulle flow and a Couette flow. To generate a clear separation of the two phases the interface must be located at
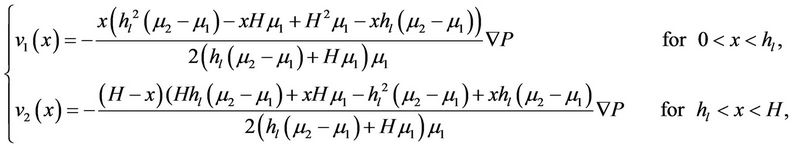 (3)
(3)
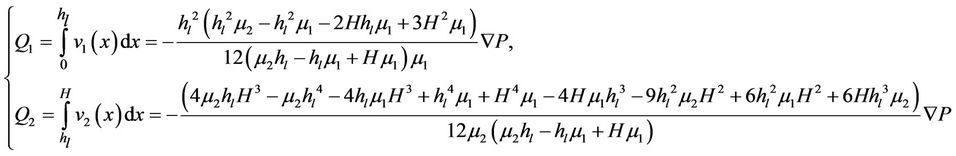 (4)
(4)
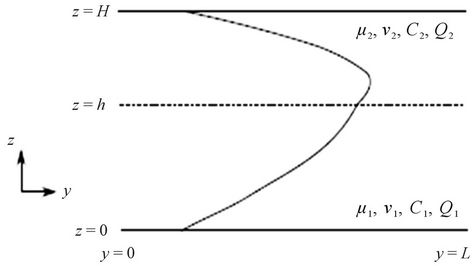
Figure 2. Schematic picture of stratified flow system showing all variables. The velocity profile shown is for μ1 > μ2, .
.
the point where the velocity is zero. Alternatively combination of electro osmotic flow with Poiseulle flow can give a counter-current flow when there are two immiscible liquids as the electric field affects the flow of only one of the two fluids. The electric field can be manipulated to increase or decrease the velocity for a fixed flow rate. This can be used to control the interface position “h”. Experimentally counter-current flow has been achieved by surface modifications of the micro-channels [10]. For the sake of mathematical simplicity the velocity in each of the phases is assumed to be uniform across the transverse direction in counter-current flow.
3. Mass Transfer in Extraction
The mass transfer behavior in stratified flow of a liquid-liquid extraction system in a micro-channel is now analysed. Here we consider the flow of a solute in the first fluid which is being extracted by the second fluid. The concentration in fluid 1, respectively 2 is represented by C1, respectively C2. Considering steady-state operation with convection in the y-direction and diffusion in the x-direction we obtain the equations which govern the behavior of the system as
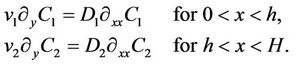 (5)
(5)
Here the expressions of v1, v2 take on distinct values for laminar, co-current and counter-current flows. At the interface we have,
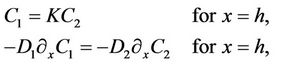 (6a)
(6a)
at the walls we have
 (6b)
(6b)
and at the inlet y = 0 we have
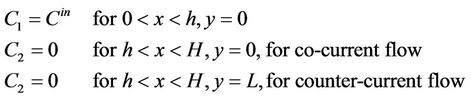 (7)
(7)
The film interface conditions result in a discontinuous concentration profile, while keeping the mass flux continuous. If K > 1, C2 remains below the value of C1 at the interface. When K < 1 the reverse is true and the second fluid extracts the solute out of the first strongly. Here the concentration C1 is depleted at the interface and we obtain a larger C2 concentration. In our computations we use Cin = 1 mol/m3.
In the co-current flow (superscript co) the concentrations of the outlet streams both tend to an equlibrium and this limits the extraction. In the counter-current flow (superscript cc) this limitation does not exist and hence the performance is much better.
For co-current (laminar or plug flow), the conservation of mass states that
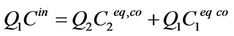
under steady-state conditions. This is valid for a long channel when the two exiting streams are in equilibrium. Hence
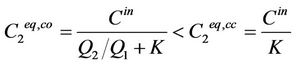
For counter-current flow the overall mass balance gives
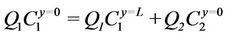
This is used to check the numerical solution. The mixed cup average concentration at a particular “y” is given by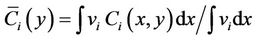 .
.
4. Analytical Solution for Co-Current Plug Flow
The convection diffusion equation can be solved analytically and elegantly under the assumptions of 1) the co-current Plug Flow Regime (PFR) when the velocity in the two fluids is uniform (v1 and v2 are constant), and 2) a constant transverse diffusion coefficient (D1 and D2). We start with non dimensionalizing the equations with respect to their characteristic lengths and initial concentrations,
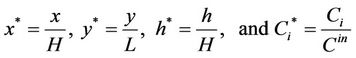
which gives the dimensionless form as
 (8)
(8)
For simplicity, we drop the superscript * from now on. We seek the solution Ci (x, y) in the form gi(y) fi(x). Substituting this in (8) gives
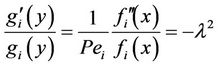
Or
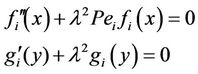 (9)
(9)
This results in an eigen value problem in the x direction whose solution is
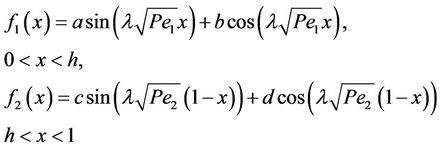 (10)
(10)
The boundary conditions at x = 0, 1 yield a = c = 0. At x = h, the boundary condition C1 = KC2 implies
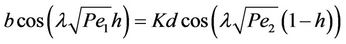 (11a)
(11a)
while  implies
implies
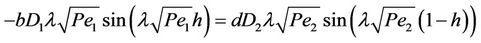 (11b)
(11b)
We seek b and d to be non-zero. This yields the characteristic equation which determines the eigen values λ as the solution to
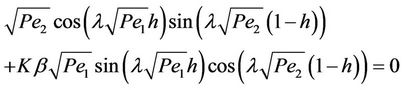 (12)
(12)
where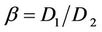 . The eigen functions corresponding to the nth eigen value is
. The eigen functions corresponding to the nth eigen value is
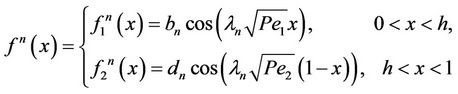 (13)
(13)
It has been shown in [13] that this system is self-adjoint in the inner product when the velocities in the two fluids are equal i.e., v1 =v2
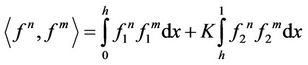 (14)
(14)
The eigen functions are normalized with respect to this inner product and the constants bn, dn are obtained as
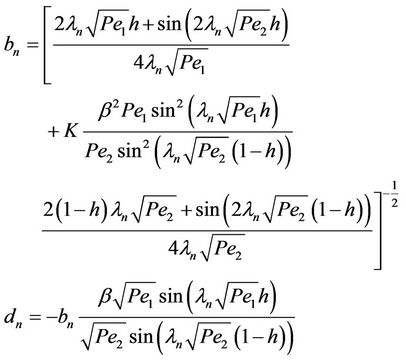 (15)
(15)
The solution for the y dependency is 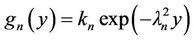 .
.
For co-current extraction the initial condition is C1 = 1 for 0 < x < h and C2 = 0 for h < x < 1. The coefficient kn can be obtained from the initial condition as
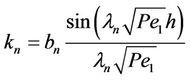
Since the boundary conditions are homogeneous Neumann in the x-direction, λ = 0 is also an eigen value, which corresponds to n = 1. The eigen-function corresponding to this is the equilibrium solution and is given by
 (16)
(16)
The complete solution to the convection diffusion equation is hence
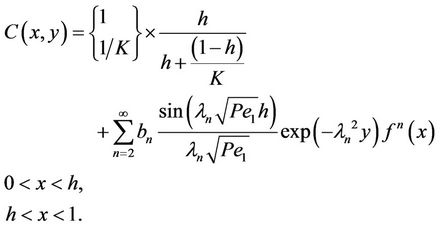 (17)
(17)
It was found that it was sufficient to take the first fifty terms in the summation in the above solution to obtain convergence. This implies that the eigen-value problem (14) is solved for the first 50 roots. Care must be taken to ensure that no roots are missed and no roots are calculated more than once. This analytical solution is used to validate the numerical code based on the method of lines with a second order finite difference scheme in the transverse direction (x). The numerical method was used to determine the concentration profiles in the laminar flow regime.
In Figure 3 we show how the analytical solution for the co-current plug flow based on the separation of variables (solid line) validates the predictions of the numerical code (points) based on finite differences. It is seen that both the average concentration as well as the concentration at a fixed y using the two approaches agree quantitatively.
The numerical code was then used to simulate the behavior for the laminar flow profile in co-current mode. Here the velocity profile obtained in Equation (3) is used to simulate the laminar behavior. The comparison of the cup-averaged concentration profiles obtained using the laminar flow and the plug flow behavior in a microchannel is shown in Figure 4. For the plug flow simulation the average velocity of the laminar flow is used. It is seen that the extraction performance under laminar flow conditions is superior to that of the plug flow conditions.
5. Numerical Solution Counter-Current Flow
For the counter-current plug flow the convective-diffusion equations are solved numerically. Two challenges arise in this and need to be addressed. These are, 1) the jump discontinuity in concentrations at the interface and 2) the inlet of the two fluid streams being at the two end points. The latter renders the system a boundary value problem.
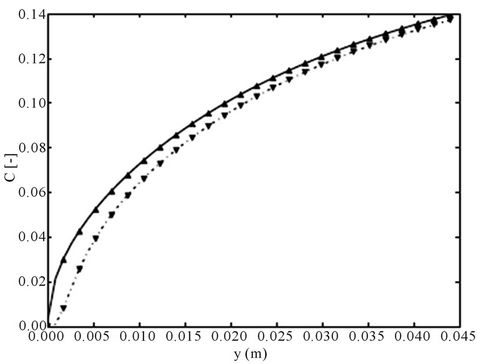
Figure 3. Comparison of the analytical solution and the numerical computation for co-current plug-flow. Here H = 4 × 10−4 m, h = 2 × 10−4 m, Q1 = Q2 = 14.2857 × 10−6 m2/s, K = 4.14, D1 = 7.4 × 10−9 m2/s, D2 = 5.64 × 10−8 m2/s. Full line is the average concentration for x > h and the dashed line the concentration at x = 0.75 H from the analytical computation. The triangles are the corresponding computed values with the numerical computation, where a grid with 100 points in the transverse direction per phase is considered.

Figure 4. Comparison of the laminar flow versus PFR with fixed Q1 and Q2. Full line is laminar flow with h = 0.42 H, K = 1/4.14, dashed line PFR with same interface position.
The numerical algorithm we use for solving the steady-state convection diffusion equation for extraction under counter-current flow is now described:
1) The channel length is divided into Ny grids in the “y” direction. The values of the solute concentrations at the interface on the fluid1 side are assumed.
2) The values of the concentrations at the interface on the fluid 2 side are obtained using the equilibrium condition.
3) Now the convection diffusion equation in each fluid is solved using the method of lines. This is possible as we have a Dirichlet boundary condition at one end (the interface) and a Neuman condition at the other end (wall) with known inlet conditions. Here a second order scheme is used to discretise the equations in the transverse direction and the equations are integrated along the axial direction.
4) After the solutions are obtained the fluxes at the Ny grid points are calculated in each fluid. The difference in the fluxes at the interface has to be zero. This condition is used to iterate on the concentrations at the interface on fluid 1 till convergence is achieved using a NewtonRaphson technique.
The above algorithm is implemented in Matlab. The cup-mixed average concentration profile along the axis obtained using the above algorithm is shown in Figure 5.
6. Simplified Model for Co-Current and Counter-Current Flow
To obtain a quick physical insight into the behavior obtained in the two flow-regimes of co-current and countercurrent flow, a simplified model is proposed in this Section. It is valid under the assumptions of a very small height H of the channel (as prevailing in micro-channels),
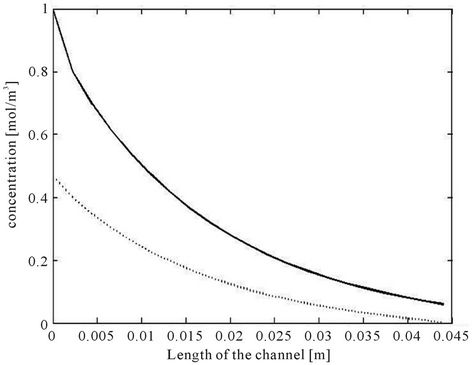
Figure 5. Concentration profiles of counter-current flow for L = 0.044 m, H = 0.0004 m, Q1 = 14.2857 × 10−6 m2/s, Q2 = 2Q1, h = H/3, D1 = 7.4 × 10−8 m2/s, D2 = D1/2, K = 1/4.14.
and large diffusion coefficients Di. Under these conditions the concentration variation in the direction transverse to the flow can be neglected and the evolution of the average concentration along the axial direction is governed by ordinary differential equations. For simplicity we assume the velocity profile to follow plug flow.
6.1. Co-Current Flow
The simplified equations of mass balance are now given by
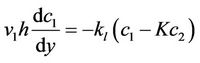 (18a)
(18a)
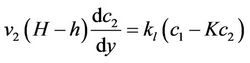 (18b)
(18b)
with 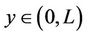 and initial condition
and initial condition
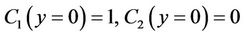
Here  represents an overall mass transfer coefficient (between the two phases). We now define
represents an overall mass transfer coefficient (between the two phases). We now define
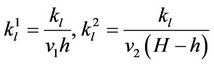
The solution to the above two equations is given by
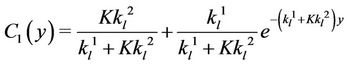 (19a)
(19a)
 (19b)
(19b)
6.2. Counter-Current Flow
The simplified equations are now given by
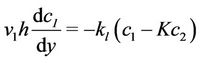 (20a)
(20a)
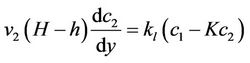 (20b)
(20b)
with initial condition
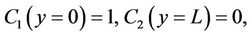
Introducing  and
and 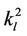 as before, the solution is given by
as before, the solution is given by
 (21a)
(21a)
 (21b)
(21b)
We now describe how the mass transfer coefficient kl can be estimated for a system experimentally.
For Co-current flow, the simplified equations (18a) and (18b) can be rearranged to yield
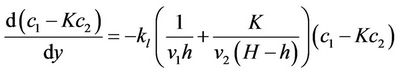 (22a)
(22a)
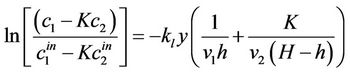 (22b)
(22b)
The rate at which mass is transferred when the concentration drops to c1 or c2 in the system is
 (23a)
(23a)
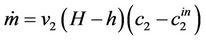 (23b)
(23b)
Using these equations, we obtain
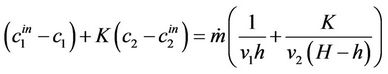
Rearranging and eliminating the terms containing the interface position “h” using (22b) we obtain
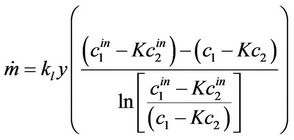 (24)
(24)
At y = L, the exit 
The logarithmic mean concentration difference is defined as
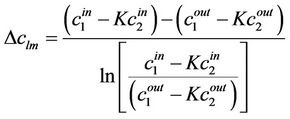 (25a)
(25a)
 (a)
(a)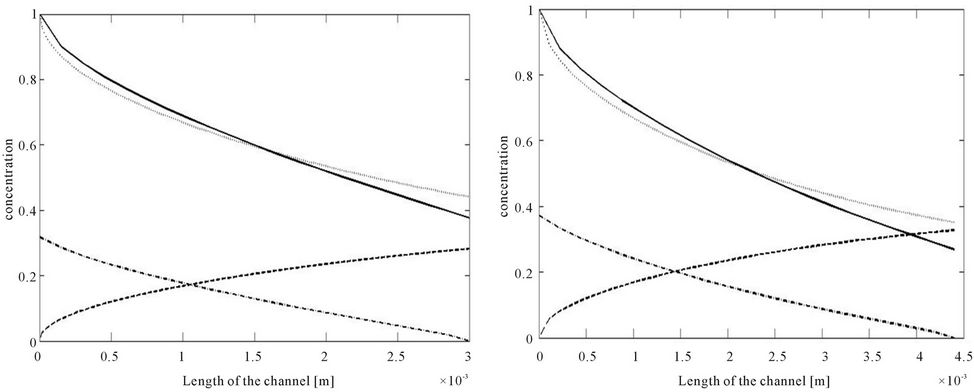 (b)
(b)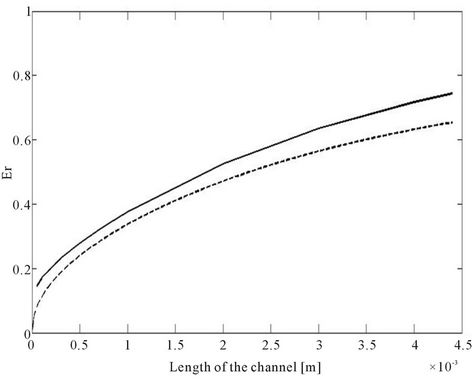 (c)
(c)
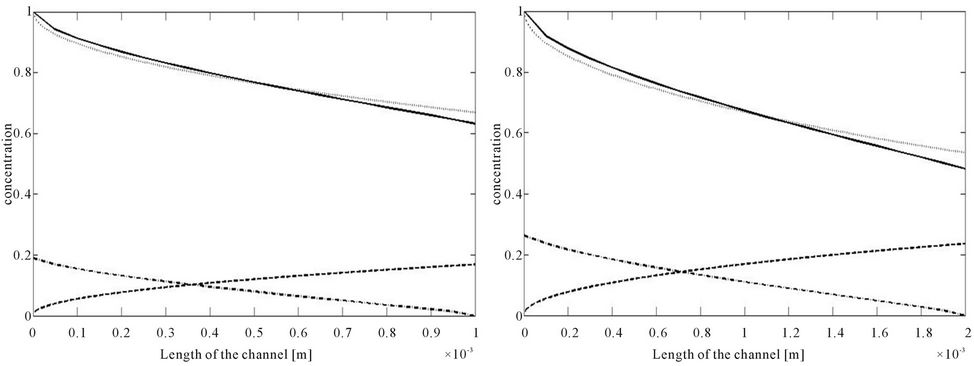
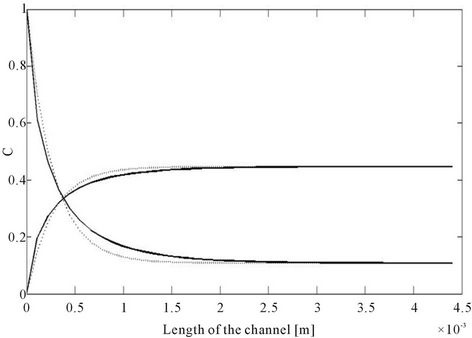
Figure 6. Co-current and counter-current extraction for L = 0.0044 m, H = 0.0004 m, Q1 = 14.2857 × 10−6, Q2 = 2Q1, h = H/3, K = 1/4.14, D1 = 4 × 7.4 × 10−8 m2/s, D2 = D1/2. (a), (b), (c), (d) Concentration profiles for L = 0.001, 0.002, 0.003, 0.0044 m, full line and dash-dot counter-current, dashed and dot co-current; (e) Extraction rate, full line counter-current, dashed co-current.
In a similar manner, kl can be calculated for countercurrent flow, using the simplified equations (20a) and (20b). Following the procedure for co-current flow it can be seen that
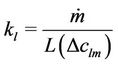 (25b)
(25b)
The mass transfer coefficient kl can also be defined using the driving force for extraction to be the deviation from equilibrium value, see Dessimoz [1]. This gives the mass transfer coefficient as
 (26)
(26)
7. Results and Discussion
In order to compare the results of our simulations and to be consistent with the literature, and evaluate the performance of a specific micro-channel set-up, we introduce some characteristic quantities. These are now defined.
Characteristic Quantities
The first is the efficiency E, defined in terms of the mixed cup concentrations as
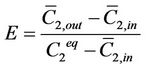 (27)
(27)
where 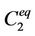 is the concentration of the solute in the second region after equilibrium is attained, and typically
is the concentration of the solute in the second region after equilibrium is attained, and typically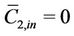 . “E” is a measure of how close the exiting stream is to equilibrium. The overall residence time tres for co-current flow is defined as
. “E” is a measure of how close the exiting stream is to equilibrium. The overall residence time tres for co-current flow is defined as
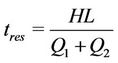 (28)
(28)
For a given length L, a unique residence time and an extraction efficiency E(L) is obtained. E = 1 corresponds to the situation when the exiting streams are in equilibrium and no further separation can take place.
The second characteristic which can describe the system is the extraction ratio Er. It represents the fraction of the amount of solute that has been fed to the system which is removed by the second fluid. This is defined as
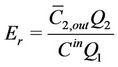 (29)
(29)
Note that for co-current flow
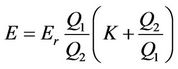 (30)
(30)
Figure 6 shows the dependency of concentration along
 (a)
(a)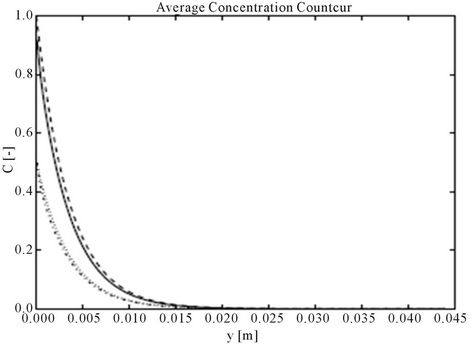 (b)
(b)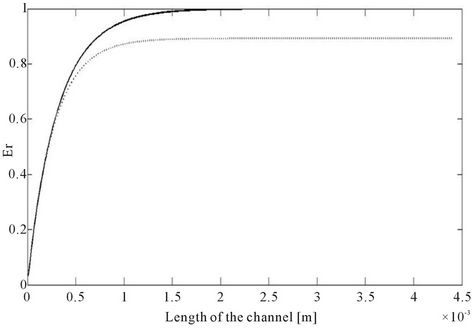 (c)
(c)
Figure 7. Co-current and counter-current extraction for L = 0.0044 m, H = 0.0004 m, Q1 = 14.2857 × 10−6, Q2 = 2Q1, h = H/3, K = 1/4.14 and large diffusion coefficient D1 = 50 × 7.4 × 10−8 m2/s, D2 = D1/2. Match with same interface height. (a) Concentration profiles co-current; (b) Concentration profiles counter-current, here full line and dash-dot are the 2D numerical computation, and dashed and dot the lumped model with matched kl value; (c) Using zero height approximation for L = 0.044 m, Extraction rate, full line counter-current, dashed co-current.
the length as obtained by solving the convective diffusion equation for co-current and counter-current extraction. Figures 6(a) to (d) shows concentration profiles for different channel lengths. For the choice of parameters it is seen that the extraction is marginally better for the counter-current operation. It is seen that as we increase the channel length the improvement in performance becomes more significant. This is verified in Figure 6(e) where the extraction ratio of the two models of operation is compared. In this last curve where we compare the extraction ratio, the curve for the co-current behavior can be obtained by a single simulation of the governing equations. However for the counter-current extraction it is necessary to simulate the behavior for each length and then compute the extraction ratio, since the problem is now a two point boundary value problem.
Figure 7 shows the performance of the co-current and counter-current systems for a different set of parameters. The diffusion coefficient has been significantly increased here. Consequently here the simplified model is expected to give a more accurate representation of the system. Here again the concentration profiles and the extraction ratios are depicted. For the concentration profiles two curves are shown: one is the prediction of the convective diffusion equation and the other is the concentration profile based on the simplified model. Here the parameter kl
 (a)
(a)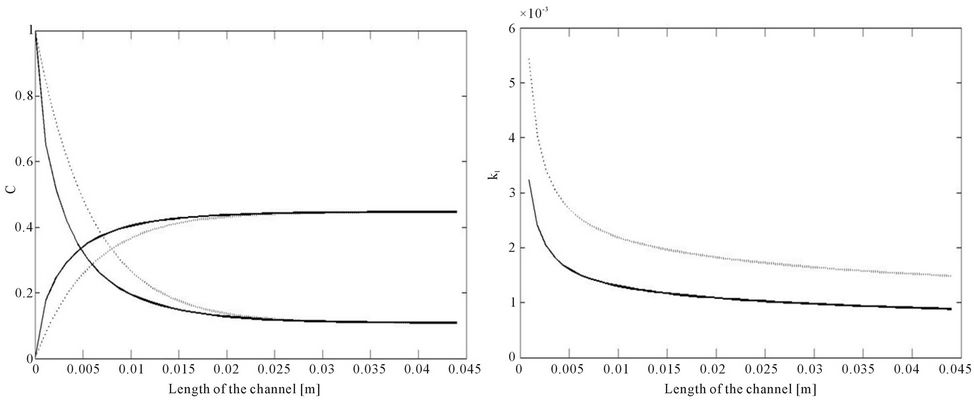 (b)
(b)
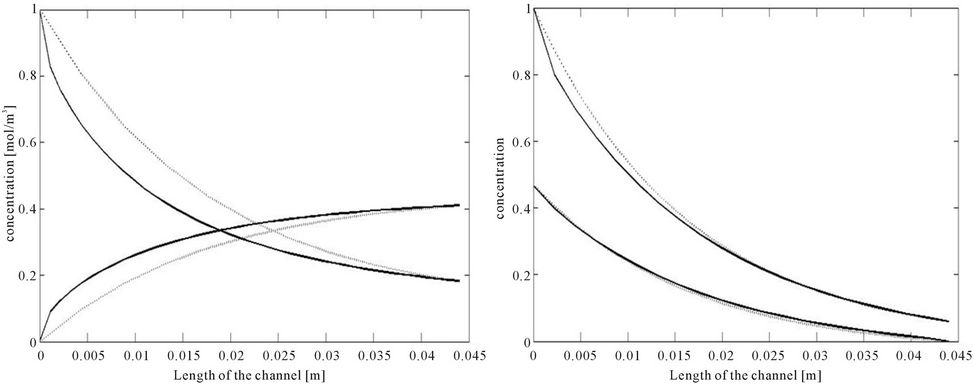
Figure 8. Comparison of PFR numerical simulation (full line) and analytical solution (dotted line) using simplified expression with kl from logarithmic mean concentration difference for L = 0.044 m, H = 0.0004 m, h = H/3, Q1 = 14.2857 × 10−6 m2/s, Q2 = 2Q1, K = 1/4.14 and D1 = 7.4 × 10−8 m2/s; D2 = D1/2, (a) Co-current concentration profiles, kl = 7.1976 × 10−4 m/s; (b) Counter-current concentration profiles, kl = 9.9793 × 10−4 m/s; (c) With large diffusion coefficient D1 = 4 × 7.4 × 10−8 m2/s, co-current concentration profiles, kl = 0.0022 m/s; (d) Comparison of kl (ΔClm ),full line and kl (eqbm), dotted line for co-current flow.
is estimated by minimizing the least squares error of the exit concentration from the two models. It can be seen that the prediction by the convective diffusion model and the simplified model agree well throughout the length of the curve.
We would like to avoid the least squares estimation of the mass transfer coefficient since this is a statistical procedure and involves fitting a parameter. For this the concentration profiles are determined solving the convective diffusion equation. The exit concentration results are used as experimental results and the log mean concentration difference is used to determine the mass transfer coefficient as described earlier. The predictions of the concentration profiles of the convective diffusion equation and the simplified model are shown in Figures 8(a) and 8(b). It is seen that the concentration profiles are in better agreement for the counter-current flow as opposed to the co-current flow. The prediction of the simplified model using the log mean concentration difference is better when the diffusion coefficient is higher and this is seen when we compare Figure 8(c) with Figure 8(a). Figure 8(d) compares the mass transfer coefficient predicted by the log mean concentration difference and the deviation from equilibrium (equation (28)). We see that the mass transfer coefficient at short lengths of the channels are high. This drops down sharply first and then slowly as the length is increased. This is to be expected since for short lengths the driving force is high and this results in a larger mass transfer coefficient. As the length increases the driving force decreases as we approach equilibrium and this lowers the mass transfer coefficient.
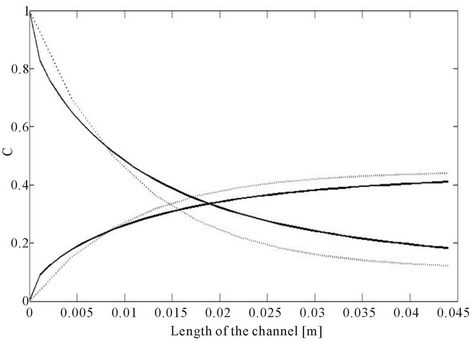
Figure 9(a) shows comparison of co-current concentration profiles obtained from the convection diffusion model and the simplified model. Here the mass transfer coefficient is calculated using the driving force as the deviation from the equilibrium concentration equation (28). Here again when the diffusivity is high we see a much better match between the axial profiles (Figure 9(b)). At the same higher diffusivity, profiles using mass transfer coefficient calculated from the deviation from equilibrium matches better than those obtained using the log mean concentration difference. (compare Figure 9(b) and 8(c)). Figure 9(c) shows a comparison of kl values calculated using the above two approaches. It is observed that mass transfer coefficients from Equation (28) are much higher than that using log mean difference at all the lengths of the channel. This difference is very high at the shorter lengths and it decreases as the length increases as observed in Figure 8(d).
8. Conclusions
In this work we have compared the performance of the co-current and countercurrent modes of operation in an
 (a)
(a) (b)
(b)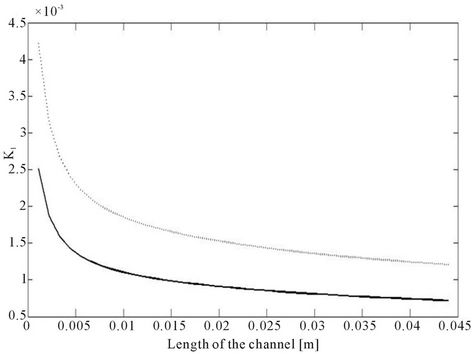 (c)
(c)
Figure 9. Comparison of PFR numerical simulation (full line) and analytical solution (dotted line) using simplified expression with kl from equilibrium concentration values for L = 0.044 m, H = 0.0004 m, h = H/3, Q1 = 14.2857 × 10−6 m2/s, Q2 = 2Q1, K = 1/4.14 and D1 = 7.4 × 10−8 m2/s; D2 = D1/2, a = 5000 m2/m3 (a) Co-current concentration profiles, kl = 1.2 × 10−3 m/s; (b) with high diffusivity, D1 = 4 × 7.4 × 10−8 m2/s, co-current concentration profiles, kl = 3.5 × 10−3 m/s; (c) comparison of kl (ΔClm), full line and kl (eqbm), dotted line.
extraction in a micro channel. This theoretical study examines the convective diffusion equation as well as a simplified model. An analytical solution is proposed for the co-current system based on the method of separation of variables. The counter-current system is solved numerically. For this a novel method which exploits the feature of the system is proposed. It is based on iterating on the interface values of the concentration. The study is numerical and shows how concepts from heat exchanger design can be extended to mass transfer systems. It is shown that the counter-current extraction is more efficient than the co-current operation. It is found that the different definitions of the mass transfer coefficient predict the behavior of the system accurately.
9. Acknowledgements
The authors thank Roger Van Keer, coordinator of the research group NaM2, for his continuous encouragement. The second author thanks the MaCKIE project (BOFGOA 01GA0405) of Ghent University which made the collaboration possible.
REFERENCES
- A.-L. Dessimoz, L. Cavin, A. Renken and L. Kiwi-Minsker, “Liquid-Liquid Two-Phase Flow Patterns and Mass Transfer Characteristics in Rectangular Micro-Reactors,” Chemical Engineering Science, Vol. 63, No. 16, 2008, pp. 4035-4044. doi:10.1016/j.ces.2008.05.005
- J. Guo and C. Ho, “Theoretical Study on Membrane Extraction of Cu2+ with d2ehpa in Laminar Flow Circular Tube Modules,” Desalination, Vol. 233, No. 1-3, 2008, pp. 247-257. doi:10.1016/j.desal.2007.09.049
- M. Liu, Y. Linu, Q. Guo and J. Yang, “Modeling of Electrosomotic Pumping of Nonconducting Liquids and Bio Fluids by a Two-Phase Flow Method,” Journal of Electroanalytical Chemistry, Vol. 636, No. 1-2, 2009, pp. 86-92. doi:10.1016/j.jelechem.2009.09.015
- Y. Gao, T. Wong, C. Yang and K. Ooi, “Two Fluid Electro Osmotic Flow in Microchannels,” Journal of Colloid and Interface Science, Vol. 284, No. 1, 2005, pp. 306-314. doi:10.1016/j.jcis.2004.10.011
- C. Wang, Y. Gao, N.-T. Nguyen, T. Wong, C. Yang and K. Ooi, “Interface Control of Pressure-Driven Two-Fluid Flow in Microchannels Using Electro-Osmosis,” Journal of Micromechanics and Microengineering, Vol. 15, 2005, pp. 2289-2297. doi:10.1088/0960-1317/15/12/011
- D. Fries, T. Voitl and P. von Rohr, “Liquid Extraction of Vanillin in Rectangular Microreactors,” Chemical Engineering & Technology, Vol. 31, No. 8, 2008, pp. 1182- 1187. doi:10.1002/ceat.200800169
- Y. Okubo, T. Maki, N. Aoki, T. H. Khoo, Y. Ohmukai and K. Mae, “Liquid-Liquid Extraction for Efficient Synthesis and Separation by Utilizing Micro Spaces,” Chemical Engineering Science, Vol. 63, No. 16, 2008, pp. 4070-4077. doi:10.1016/j.ces.2008.05.017
- P. Znidarsic Plazl and I. Plazl, “Steroid Extraction in a Microchannel System-Mathematical Modelling and Experiments,” Lab on Chip, Vol. 7, 2007, pp. 883-889. doi:10.1039/b704432a
- W. E. TeGrotenhuis, R. J. Cameron, M. G. Butcher and P. M. W. R. S. Martin, “Microchannel Devices for Efficient Contacting of Liquids in Solvent Extraction,” Separation Science and Technology, Vol. 34, 1999, pp. 951-974. doi:10.1081/SS-100100691
- A. Aota, M. Nonaka, A. Hibara and T. Kitamori, “Countercurrent Laminar Microflow for Highly Efficient Solvent Extraction,” Angewandte Chemie, Vol. 119, No. 6, 2007, pp. 896-898. doi:10.1002/ange.200600122
- A. Hibara, M. Nonaka, H. Hisamoto, K. Uchiyama, Y. Kikutani, M. Tokeshi and T. Kitamori, “Stabilization of Liquid Interface and Control of Two-Phase Confluence and Separation in Glass Microchips by Utilizing Octadecylsilane Modification of Microchannels,” Analytical Chemistry, Vol. 74, No. 7, 2002, pp. 1724-1728. doi:10.1021/ac011038c
- A. Aota, H. Akihide, S. Kyosuke, S. Yasuhiko, O. Koji and T. Kitamori, “Flow Velocity Profile of Micro Counter-Current Flows,” Analytical Science, Vol. 23, No. 2, 2007, pp. 131-133. doi:10.2116/analsci.23.131
- D. Ramakrishna and N. R. Amundson, “Transport in Composite Materials: Reduction to a Self-Adjoint Formalism,” Chemical Engineering Science, Vol. 29, No. 6, 1974, pp. 1457-1464. doi:10.1016/0009-2509(74)80170-3
NOTES
*Corresponding author.

