Applied Mathematics
Vol. 3 No. 6 (2012) , Article ID: 20283 , 3 pages DOI:10.4236/am.2012.36090
Some Properties on the Function Involving the Gamma Function
Department of Mathematics and Information Science, Weinan Normal University, Weinan, China
Email: ccbb3344@163.com
Received April 25, 2010; revised May 25, 2012; accepted June 2, 2012
Keywords: Gamma Function; Monotonicity; Convexity; Inequality
ABSTRACT
We studied the monotonicity and Convexity properties of the new functions involving the gamma function, and get the general conclusion that Minc-Sathre and C. P. Chen-G. Wang’s inequality are extended and refined.
1. Introduction
The classical gamma function 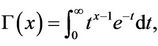
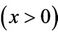 is one of the most important functions in analysis and its applications. The logarithmic derivative of the gamma function can be expressed in terms of the series
is one of the most important functions in analysis and its applications. The logarithmic derivative of the gamma function can be expressed in terms of the series
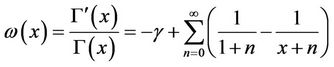 (1)
(1)
(x > 0; 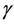 = 0.57721566490153286… is the Euler’s constant), which is known in literature as psi or digamma function. We conclude from (1) by differentiation
= 0.57721566490153286… is the Euler’s constant), which is known in literature as psi or digamma function. We conclude from (1) by differentiation
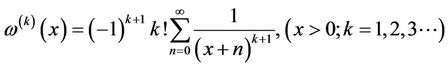 (2)
(2)
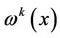 are called polygamma functions.
are called polygamma functions.
H. Minc and L. Sathre [1] proved that the inequality
 (3)
(3)
is valid for all natural numbers n. The Inequality (3) can be refined and generalized as (see [2-4])
 (4)
(4)
where k is a nonnegative integer, n and m are natural numbers. For , the equality in (4) is valid. The Inequality (4) can be written as
, the equality in (4) is valid. The Inequality (4) can be written as
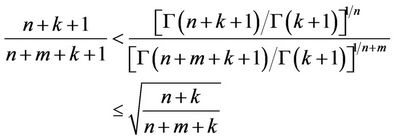 (5)
(5)
In 1985, D. Kershaw and A. Laforgia [5] showed the function  is strictly decreasing and
is strictly decreasing and  strictly increasing on
strictly increasing on , from which the Inequality (3) can be derived. In 2003, B.-N. Guo and F. Qi [2] proved that the function
, from which the Inequality (3) can be derived. In 2003, B.-N. Guo and F. Qi [2] proved that the function 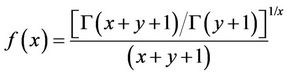 is decreasing in
is decreasing in 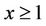 for fixed
for fixed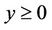 , from which the left-hand side inequality of (5) can be obtained. In the 2009, C. P. Chen-G. Wang had obtained the extended inequality of the function above. They gave the limits of it and other results.
, from which the left-hand side inequality of (5) can be obtained. In the 2009, C. P. Chen-G. Wang had obtained the extended inequality of the function above. They gave the limits of it and other results.
In this paper, our Theorem 1 considers the monotonicity and logarithmic convexity of the new function g on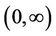 . This extends and generalizes B.-N. Guo and F. Qi’s [2] as well as C. P. Chen and G. Wang’s [6] results.
. This extends and generalizes B.-N. Guo and F. Qi’s [2] as well as C. P. Chen and G. Wang’s [6] results.
Theorem 1. Let fixed  and
and 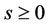 be real number, then the new function
be real number, then the new function
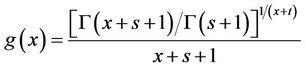
is strictly decreasing and strictly logarithmically convex on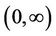 , Moreover,
, Moreover,
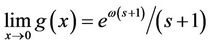 and
and 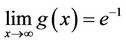
Theorem 2. Let 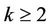 be an positive integer,
be an positive integer, 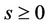 be real number, then the function
be real number, then the function
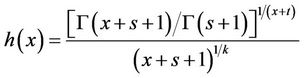
is strictly increasing on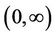 .
.
2. Proof of the Theorems
Proof of Theorem 1. First, we define for fixed 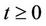 and
and ,
,

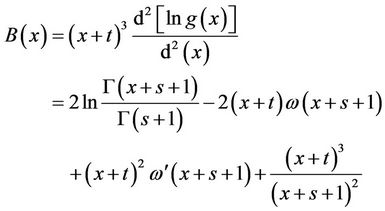
From the differentiation of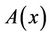 , we should have
, we should have

Hence, the function 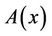 is strictly decreasing and
is strictly decreasing and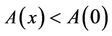 , for
, for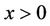 , which yields the desired result that
, which yields the desired result that  for
for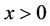 .
.
Using the asymptotic expansion [7, p. 257]

and
 (6)
(6)
we can conclude that .
.
By L’Hospital rule, we conclude from (6) that
Then from the Differentiation of  yields
yields
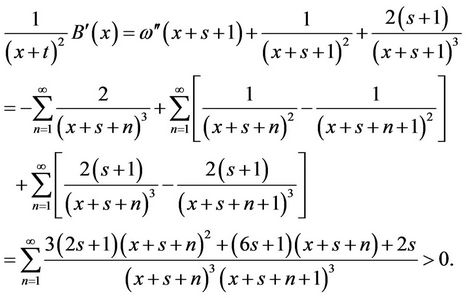
Hence, the function 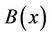 is strictly increasing and
is strictly increasing and  for
for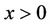 , which yields the desired result that
, which yields the desired result that 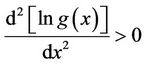 for
for .
.
Proof of Theorem 2. Define for 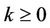 be an positive integer and
be an positive integer and ,
,

Differentiation of  gives
gives

Hence, the function 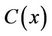 is strictly increasing and
is strictly increasing and 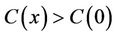 for
for 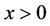 which yields the desired result that
which yields the desired result that 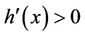 for
for .
.
3. Use the Theorem
From the proof above the following corollaries are obvious.
Corollary 1. Let fixed 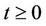 and
and 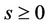 be a real number, then for all real numbers
be a real number, then for all real numbers ,
,
 (7)
(7)
Both bounds in (7) are best possible.
Corollary 2. Let fixed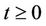 ,
, 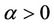 and
and 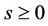 be real numbers,
be real numbers,  be an positive integer, then for all real numbers
be an positive integer, then for all real numbers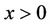 ,
,
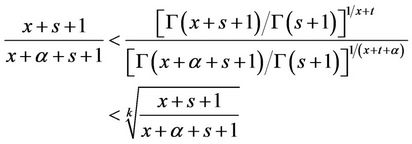 (8)
(8)
In particular, taking in (8)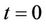 ,
,  , we obtain the result that Minc-Sathre and C. P. Chen-G. Wang got
, we obtain the result that Minc-Sathre and C. P. Chen-G. Wang got
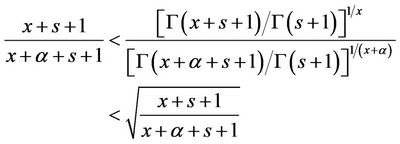 (9)
(9)
The inequality is an improvement of above, and we can extend it as the below form.
Corollary 3. Let , we have
, we have
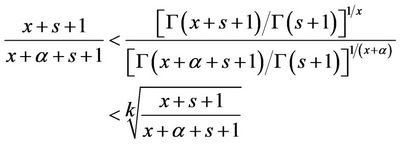 (10)
(10)
In most particular, weobtain Corollary 4. Let t be an positive integer, we get
 (11)
(11)
and for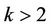 ,
,
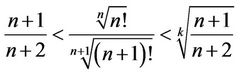 (12)
(12)
Corollary 5. Let t be an positive integer, we get
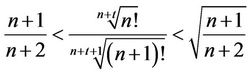 (13)
(13)
The Inequality (13) is an improvement of (3).
4. Acknowledgements
Foundation item: Supported by SFC (11071194), Scientific Research Program Funded by Shaanxi Provincial Education Department (Program No 12JK0880) Shaanxi Provincial Natural Foundation (2012JM1021), Weinan Normal University Foundation (12YKS024), Key help subjects of Shaanxi Provincial Foundation. State Key Laboratory of Information Security (Institute of Software, Chinese Academy of Sciences100190) (2011NO: 01-01- 2).
REFERENCES
- H. Minc and L. Sathre, “Some Inequalities Involving
 ,” Proceedings of the Edinburgh Mathematical Society, Vol. 14, No. 65, 1964, pp. 41-46. doi:10.1017/S0013091500011214
,” Proceedings of the Edinburgh Mathematical Society, Vol. 14, No. 65, 1964, pp. 41-46. doi:10.1017/S0013091500011214 - B.-N. Guo and F. Qi, “Inequalities and Monotonicity for the Ratio of Gamma Functions,” Taiwanese Journal of Mathematics, Vol. 7, No. 2, 2003, pp. 239-247.
- F. Qi, “Inequalities and Monotonicity of Sequences Involving
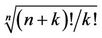 ,” Soochow Journal of Mathematics, Vol. 29, No. 4, 2003, pp. 353-361.
,” Soochow Journal of Mathematics, Vol. 29, No. 4, 2003, pp. 353-361. - F. Qi and Q.-M. Luo, “Generalization of H. Minc and J. Sathre’s Inequality,” Tamkang Journal of Mathematics, Vol. 31, No. 2, 2000, pp. 145-148.
- D. Kershaw and A. Laforgia, “Monotonicity Results for the Gamma Function,” Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur., Vol. 119, 1985, pp. 127-133.
- C.-P. Chen and G. Wang, “Monotonicity and Logarithmic Convexity Properties for the Gamma Function,” Scientia, Vol. 5, No. 1, 2009, pp. 51-54.
- M. Abramowitz and I. A. Stegun (Eds.), “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards,” Applied Mathematics Series, 4th Printing, Washington, Vol. 55, 1965.

