ABSTRACT

In this paper we deal with a cubic near-Hamiltonian system whose unperturbed system is a simple cubic Hamiltonian system having a nilpotent center. We prove that the system can have 5 limit cycles by using bifurcation theory.

1. Introduction

In the International Congress of Mathematics held in Paris in 1900, Hilbert made a list of 23 problems. The second part of Hilbert’s 16th problem is still an open and difficult question: to find a upper bound of the number of limit cycles and their relative locations in polynomial vector fields of order n.

If the singular point of the system is a non-saddle, nor nilpotent, the related Hopf bifurcations are elementary, see [1-3] and their references. Hopf bifurcations from the elementary focus type of singularities have found broad and important applications in biology, chemistry and physics and engineering, see [4-7] for examples. Yet for the bifurcation of limit cycles from a non-elementary center in a more general planar vector field, its intrinsic dynamics is still far away from understanding due to the complexity and technical difficulties in dealing with such bifurcations.

Then it was natural to restrict the study of the nilpotent center by assuming the system is a perturbation of a Hamiltonian system. Consider the following system

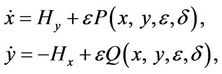(1.1)

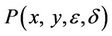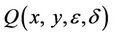where, and are 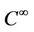functions, is small and with D a compact set.

When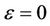, system (1.1) becomes

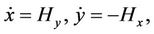(1.2)

which is Hamiltonian system. Now suppose that the Hamiltonian system (1.2) has a nilpotent center at the origin, namely the function H satisfies the following conditions:

(H1) 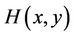is a 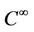function, satisfying

;

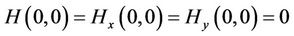(H2)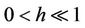, the equation 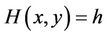defines a closed curve L_h surrounding the origin and L_h approaches the origin as h goes to zero;

(H3) ,.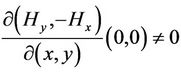

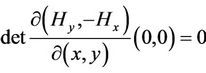It follows that the expansion of H at the origin has the form

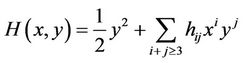
Assume that the equation 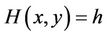intersects the positive x-axis a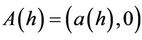t. Let 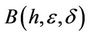denote the first intersection point of the positive orbit of (1.1) starting at 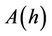with the positive x-axis. Then, we have

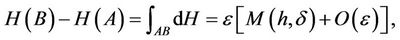(1.3)

where

(1.4)

The Abelian integral M above is called the first order Melnikov function of system (1.1). From Han [8], we have a general theorem as follows.

Theorem 1.1. Suppose that the origin is nilpotent singular point 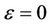and that 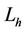approaches the origin as h goes to zero. If there exist an integer 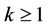and 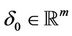such that

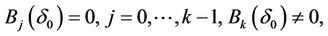
and

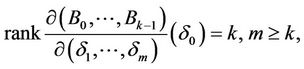
then we have 1) 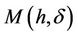has at most k zeros nea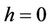r for 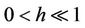and all 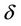near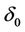, and k zeros can appear for some 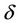near.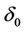

2) System (1.1) has at least k limit cycles near the origin for some 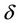near.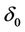

2. Main Results and Proof

Consider the following near-Hamiltonian system:

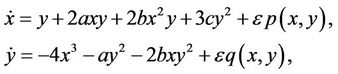(2.1)

where 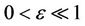and p and q are cubic polynomials. We can write

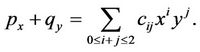(2.2)

Then unperturbed system 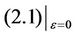is a Hamiltonian system with Hamiltonian

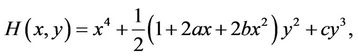(2.3)

system 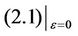has a nilpotent center at the origin. Let be the closed curve defined by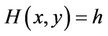. Then it can be presented as

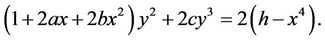(2.4)

Assume that the positive solution of the above equation in y is

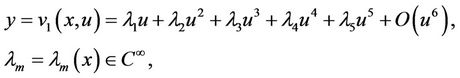(2.5)

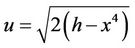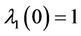where and. Then by (2.4) and (2.5) we obtain

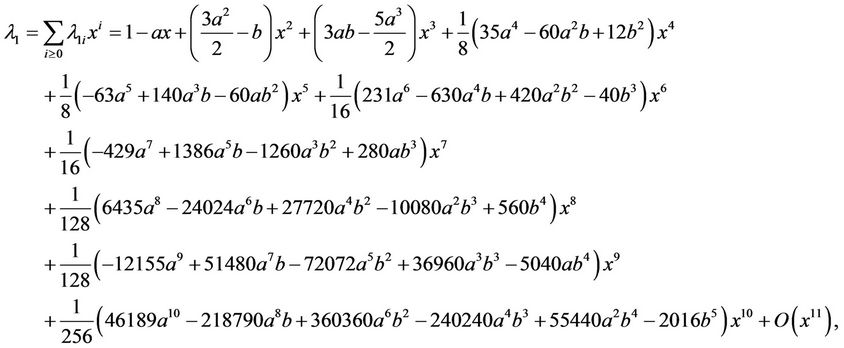
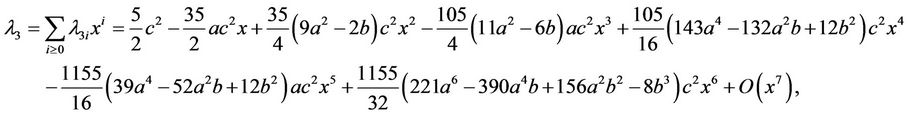
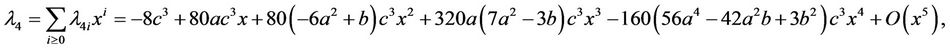
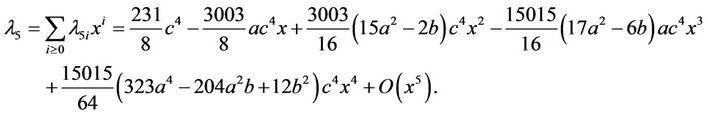
By [8] the negative solution of (2.4) in y satisfies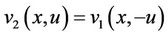. Thus, two solutions of (2.4) are

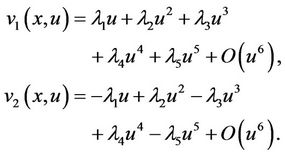(2.6)

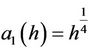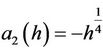On the other hand, the intersection points of L_h and xaxis have the x-coordinates and. Then by (2.2) we can write

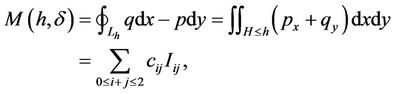(2.7)

where

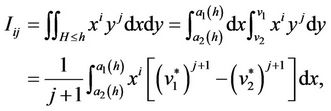(2.8)

Here,

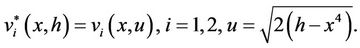
Introduce

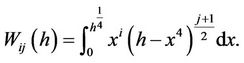(2.9)

Then, similar to the method of Han [8] we have

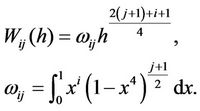(2.10)

Therefore, in turn by (2.6)-(2.10) we have

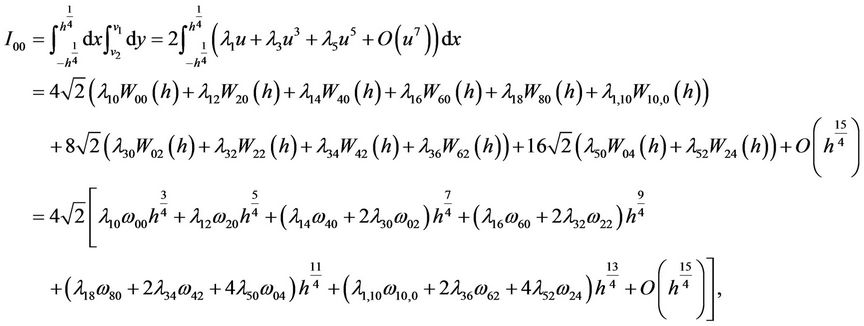
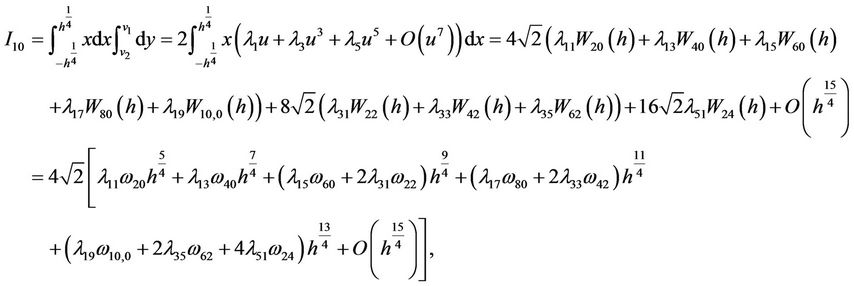
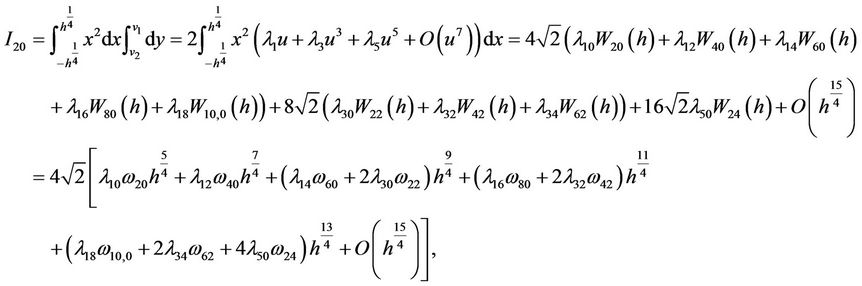
Noting that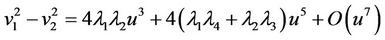, then similarly we have

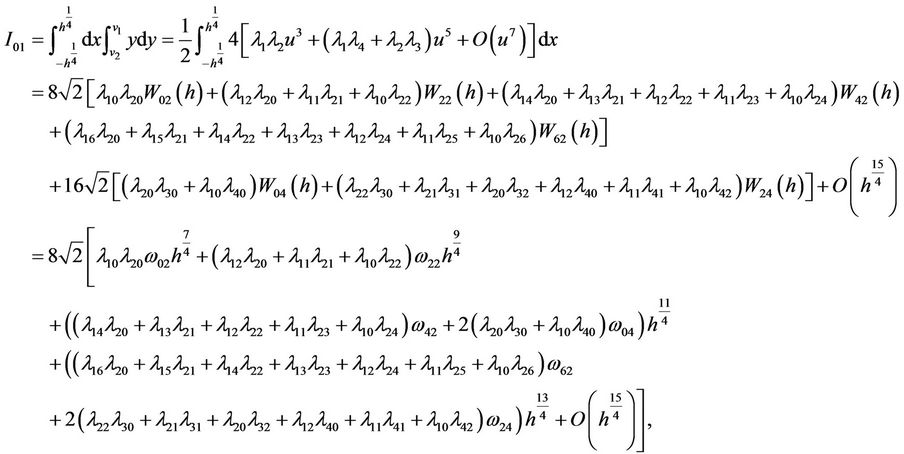
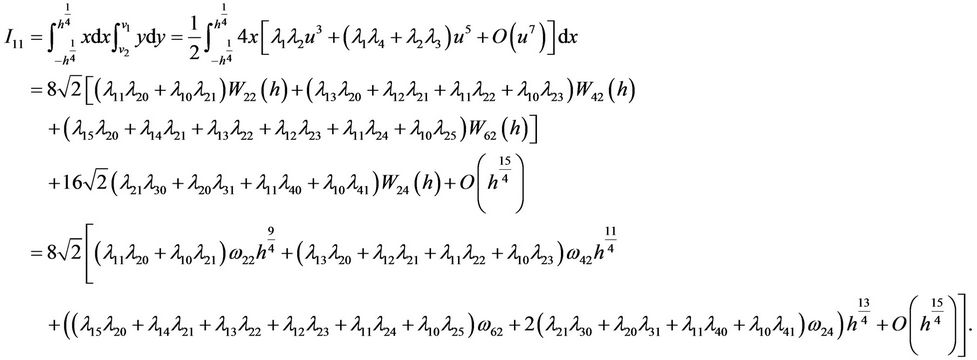
In the same way, using, we have

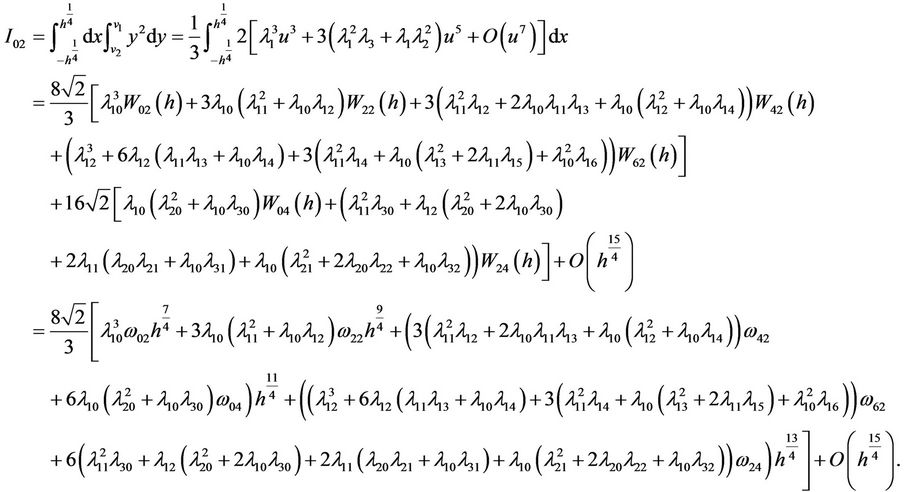
Hence, we have

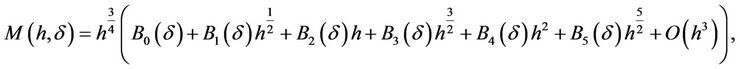
where And

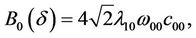
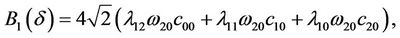
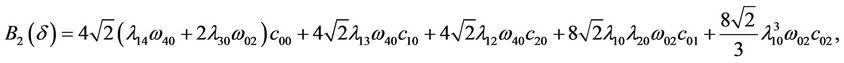
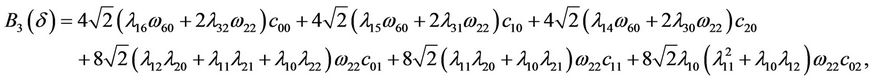
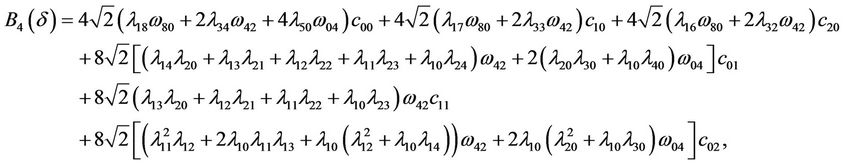
Now it is direct that

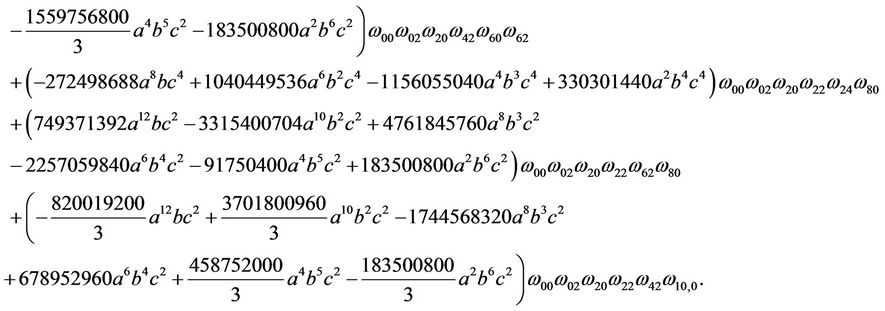
Here, if let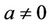, , 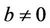, 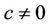then for some cubic system (2.1) we can obtain the above determinant is not zero, then the function M can have 5 simple zeros in h > 0 near h = 0 for some 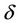near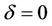. For example, let

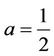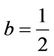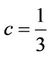, , , we obtain from the above formula

Here,

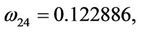
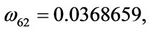
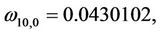
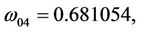
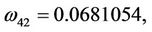
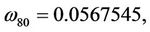
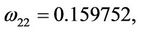
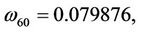
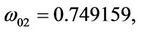
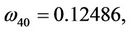
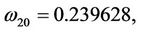
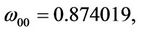
then we can obtain

(2.11)

By Theorem 1.1 we have:

Theorem 2.1. The function 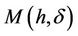has at most 5 zeros in 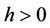near, and for 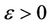small the cubic system (2.1) can have 5 limit cycles near the origin.

REFERENCES

NOTES

^*The research was partially supported by National Natural Science Foundation of China (71101088).