International Journal of Geosciences
Vol.3 No.5(2012), Article ID:25025,8 pages DOI:10.4236/ijg.2012.35116
Software to Estimate Earthquake Spectral and Source Parameters
Department of Earthquake Engineering, Indian Institute of Technology, Roorkee, India
Email: *arjundeq@gmail.com
Received September 19, 2012; revised October 21, 2012; accepted November 11, 2012
Keywords: Spectral Parameters; Source Parameters; EQ_SRC_PARA; Garhwal; Uttarkashi
ABSTRACT
A software (EQK_SRC_PARA) has been developed to estimate spectral parameters of earthquake source spectrum, namely: low frequency displacement spectral level (Ω0), corner frequency above which spectrum decays with a rate of 2 (fc), the cut-off frequency above which the spectrum again decays (fmax) and the rate of decay above fmax (N). A Brune’s source model [1,2] that yield a fall-off of 2 beyond corner frequency is considered with high cut-off frequency factor presented by Boore [3] that fits well for frequencies greater than fmax. The software EQK_SRC_PARA is written in MATLAB and uses input data in Sesame ASCII Format (SAF) format. The obtained spectral parameters have been used to estimate source parameters (e.g., seismic moment, source dimension and stress drop etc.) and to develop scaling laws for the study region. The cut-off frequency “fmax” can also be studied and interpreted to confirm about its origin.
1. Introduction
The seismic design of engineered structures depends upon a quantitative estimate of the characteristics of strong ground motion at desired site. In case recorded data are not available at that site, then simulation of ground motion is the only way for engineers to rely upon. The stochastic approach is the most popular way, which requires the knowledge of spectral and source parameters (e.g., corner frequency and stress drop) of study region and has very good results recently in both regions with and without recordings. The shape of the seismic spectrum and how it scales with earthquake size has been a topic of importance as a way of gaining insight into the character of earthquake source processes and a guide to the simulation of strong ground motion for engineering purposes [4]. In this direction, Aki [5] examined the dependence of the amplitude spectrum of seismic waves on source size and derived scaling relation of earthquake source spectra based on ω2 model. Satisfactory agreement has been found with observations based on the assumption of similarity. A constant stress drop has been considered, however, it is pointed out that if the stress drop differs, the scaling law will not apply and if the stress drop varies systematically with respect to environmental factors as focal depth, orientation of the fault plane and crust-mantle structure, different scaling laws can be constructed for different environments.
Brune [1,2] modeled an earthquake source as a tangential stress pulse applied instantaneously to the interior of a dislocation surface. This model employs three independent parameters (moment, source dimension and fractional stress drop) those determine the shape of the farfield displacement spectrum of body waves. The relationship of the corner frequency to the fault radius has been constrained by assuming that the effective stress was equal to the average static stress drop. This model has been extensively used to estimate source parameters from the observational data of seismic waves [6-12].
In these models, the displacement source spectrum has a simple ω2 shape, i.e., it has a flat level for frequencies below a source-corner frequency (fc) and a decay of ω−2 for frequencies greater than source-corner frequency. Similarly, the acceleration the acceleration spectrum has ω2 shape for frequencies below a source-corner frequency (fc) and a flat level for frequencies greater than source-corner frequency. Hanks [13] observed that there is another frequency called the maximum cut-off frequency fmax, above which acceleration spectral amplitudes diminish abruptly. This cut-off frequency, fmax, is an important parameter from earthquake engineering point as it controls the peak ground acceleration. There is a controversy about its origin. Hanks [13] and Anderson and Hough [14], among others, contend that fmax is a recording site effect. However, most of the studies attribute this due to source [15-24].
A software has been developed employing Brune’s source model [1,2] and a high-cut filter presented by Boore [3] to estimate spectral parameters of source spectrum, namely: low frequency displacement spectral level (Ω0), corner frequency above which spectrum decays with a rate of 2 (fc), the frequency above which the spectrum again decays (fmax) and the rate of decay above fmax (N). These spectral parameters are used to estimate source parameters and to develop scaling laws. The source parameters of an earthquake of 21st September 2009 (Mw 4.7) that occurred near Uttarkashi have been estimated by this software as an example.
2. Methodology
The time histories are first corrected for instrument response and then rotated to obtained SH-component of ground motion. The SH-spectrum is corrected for attenuation due to path. In this study Brune’s source model [1, 2] that yield a fall-off of 2 beyond corner frequency is considered with high frequency dimunition factor, a Butterworth high-cut filter presented by Boore [3] that fits well for frequencies greater than fmax is fitted in observed acceleration spectrum as
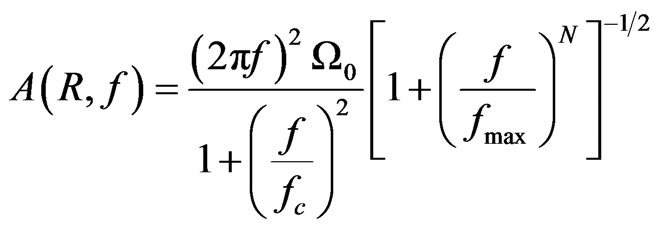 (1)
(1)
And for displacement spectrum
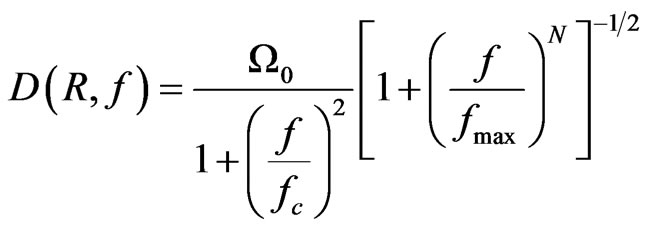 (2)
(2)
The software automatically picks the spectral parameters:
1) low frequency displacement spectral level, Ω02) corner frequency above which spectrum decays with a rate of 2, fc3) the frequency above which the spectrum again decays, fmax and 4) the rate of decay above fmax, N.
A brief explanation to the technique has been presented here with an example data of Srikot (SRIK) station for 21st September 2009 earthquake (Mw = 4.7) that occurred near Uttarkashi. The time histories are first corrected for instrument response using transfer function estimated from zero-poles values and then rotated about azimuth to obtained SH-component of ground motion. A typical example of selected SH-component of time history obtained after applying instrument response and rotation about azimuth is shown in Figure 1.
The Fast Fourier Transform (FFT) of selected SHcomponent of time history is performed to obtain spectrum of SH-component. A frequency dependent attenua-
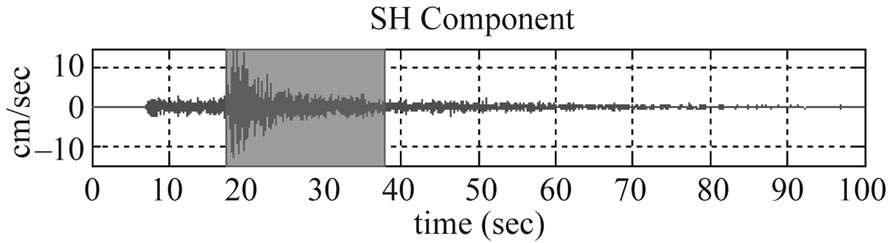
Figure 1. An example of selected SH-component of velocity time history obtained after applying instrument response and rotation about azimuth of an earthquake (Mw 4.7) recorded at Srikot (SRIK) on short period seismograph.
tion correction, Qc = 110f1.02 [25] has been applied to spectrum of SH-component to account for path effect. An estimate of fc is obtained from velocity spectrum; it is a value of frequency where the velocity spectrum has a peak. This is shown in log-log plot in Figure 2(a), however, this peak on log-linear scale becomes more clear as shown in Figure 2(b).
Then a value of fmax is estimated from snap (double differential of acceleration, snap (f) = ω2 A (f)), it is approximately a value of frequency where spectral snap has a peak. This is shown in Figure 3(a) log-log plot and for more clarity in Figure 3(b) log-linear scale.
Glassmoyer and Borcherdt [26] related “fc” is to the constant spectral levels of displacement “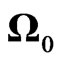 ” and acceleration “
” and acceleration “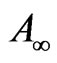 ” as given below:
” as given below:
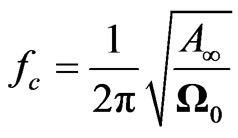 (3)
(3)
Glassmoyer and Borcherdt [26] considered “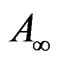 ” flat or constant spectral level for acceleration spectrum above fc. However in this study, “
” flat or constant spectral level for acceleration spectrum above fc. However in this study, “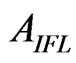 ” shown in Figure 4(a) is a flat or constant spectral level of acceleration amplitude spectrum for intermediate frequencies between fc and fmax. This leads to the approximation of “
” shown in Figure 4(a) is a flat or constant spectral level of acceleration amplitude spectrum for intermediate frequencies between fc and fmax. This leads to the approximation of “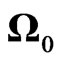 ” shown in Figure 4(b) thorough the value of acceleration’s constant amplitude spectral level “
” shown in Figure 4(b) thorough the value of acceleration’s constant amplitude spectral level “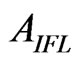 ” as:
” as:
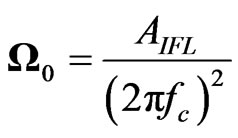 (4)
(4)
The source model for acceleration spectrum given by Equation (1) is fitted to observed spectrum with different values of fc between f1 and fmax, and for fmax between fc and fNy (Nyquest frequency) and its value is obtained from observed and modeled spectra based on root mean square error (rmse). Plot in Figure 5(a) shows the values of fc between f1 and fmax and the difference in observed and modeled spectra, the value for fc is considered where the root mean square error (rmse) is minimum. Similary Figure 5(b) shows the values of fmax between fc and fNq and the difference in observed and modeled spectra; the value for fmax is considered where the root mean square error (rmse) is least.
Then the corrected value of Ω0 is obtained from relation (4). Finally, values of N between 2 to 10 are given and
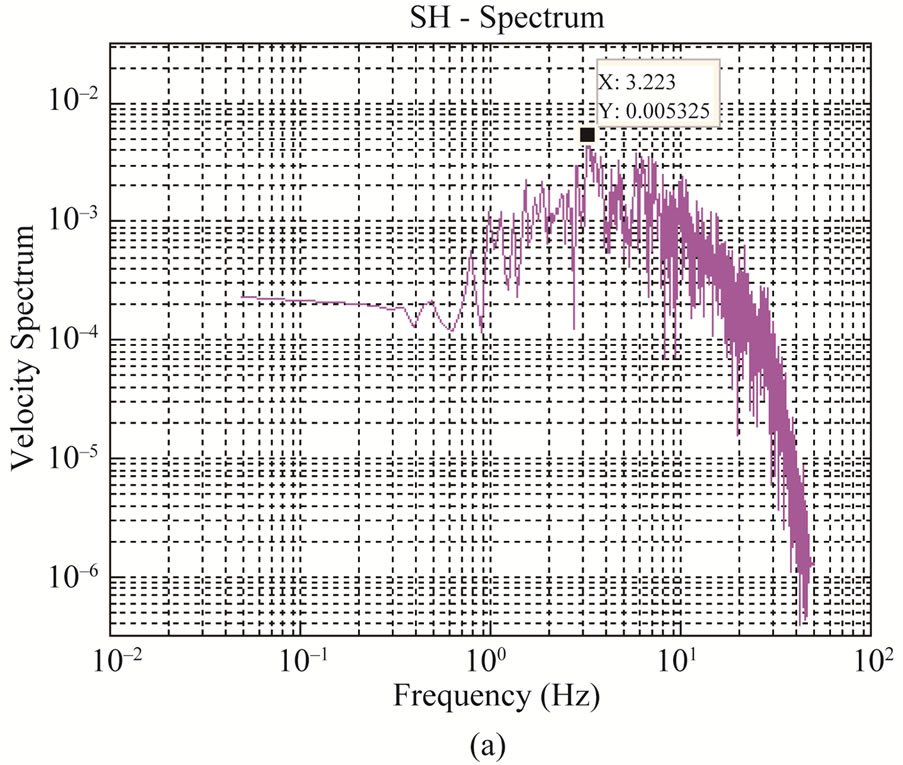
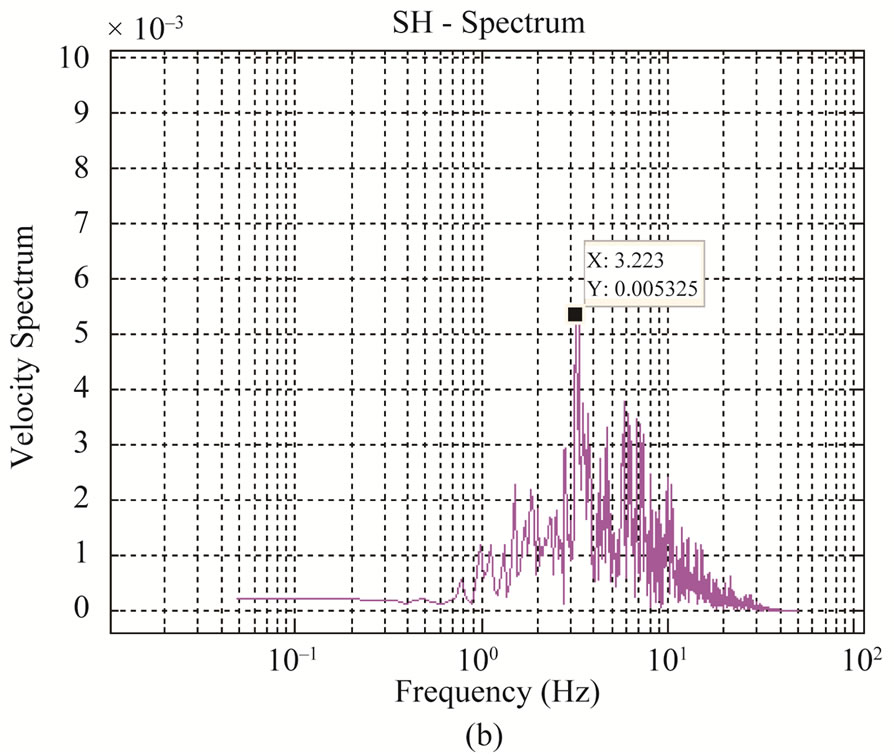
Figure 2. Plot of velocity spectrum for estimation of fc—it is a value of frequency where the velocity spectrum has a peak value shown on left (a) log-log plot and on right (b) log-linear plot.
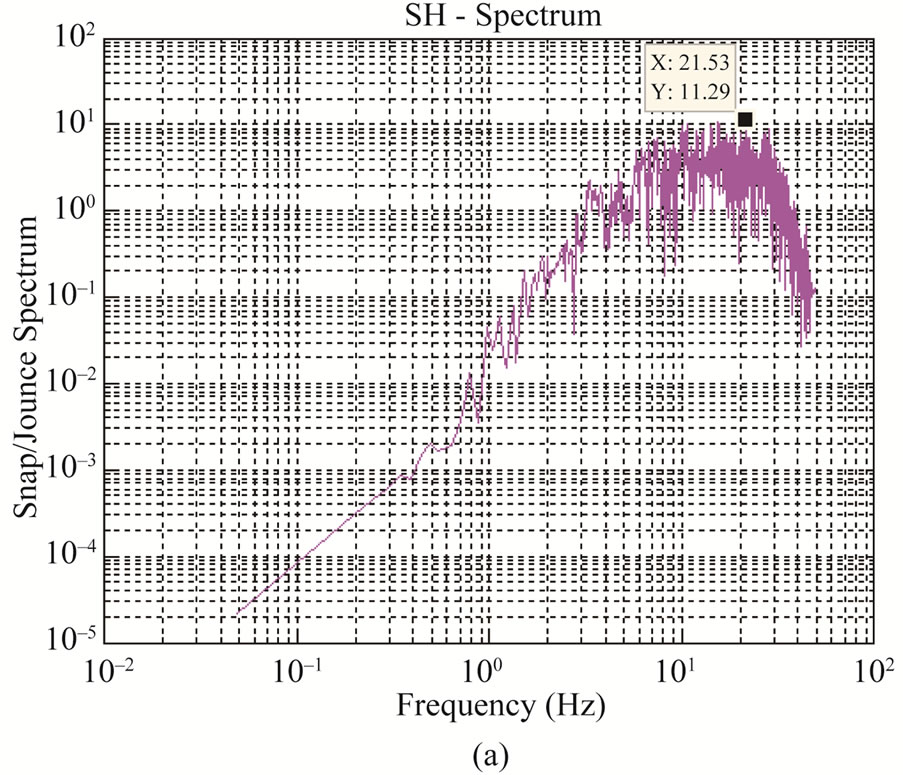
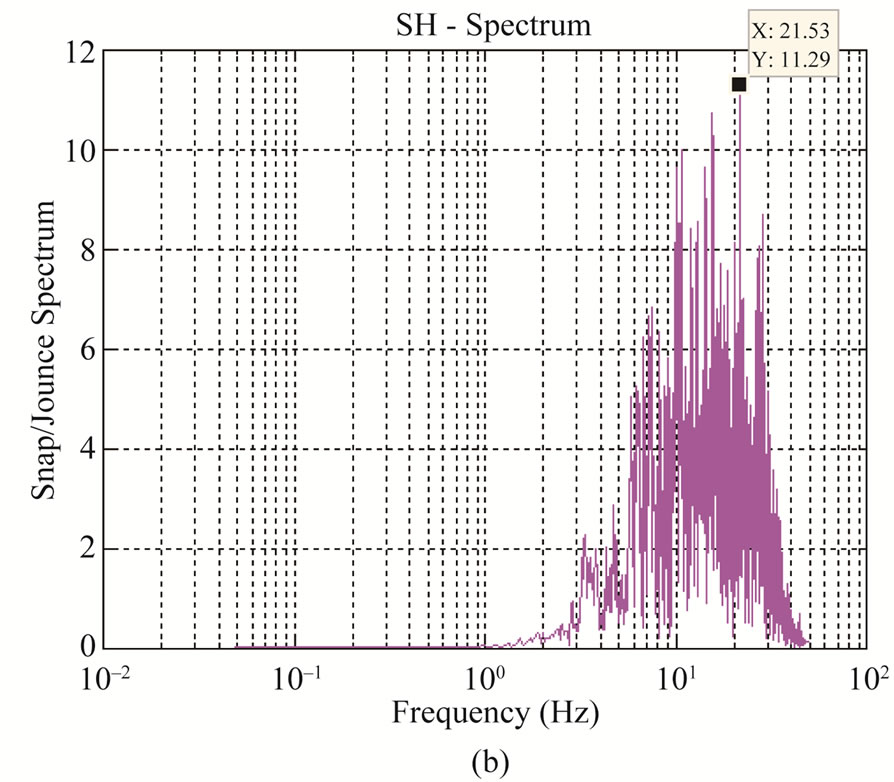
Figure 3. Plot of snap/jounce spectrum for estimation of fmax—it is a value of frequency where the snap/jounce spectrum has a peak value shown on left (a) log-log plot and on right (b) log-linear plot.
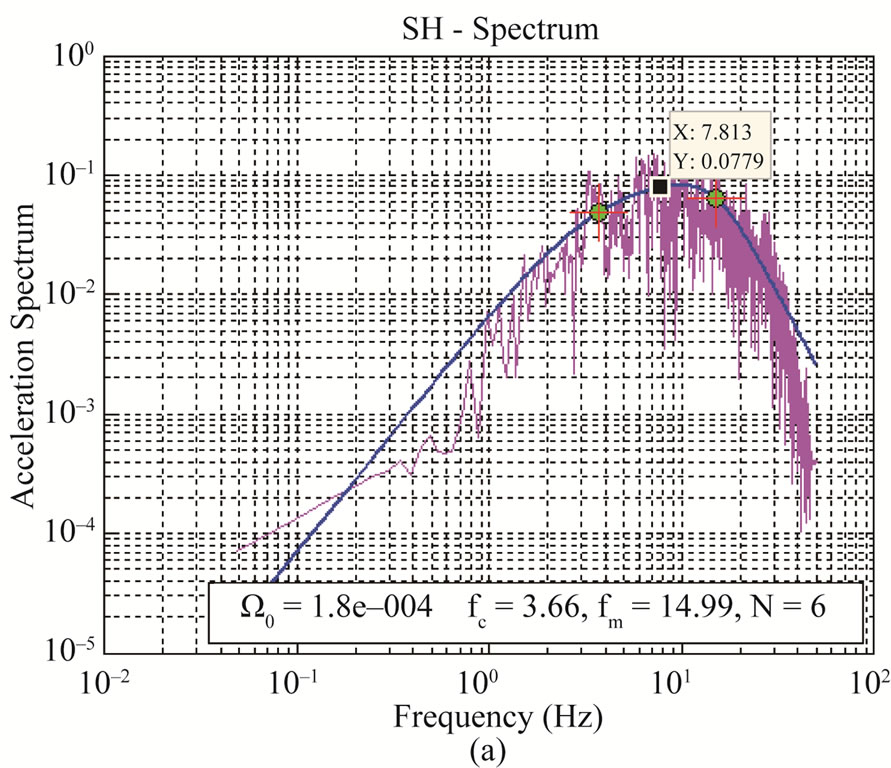
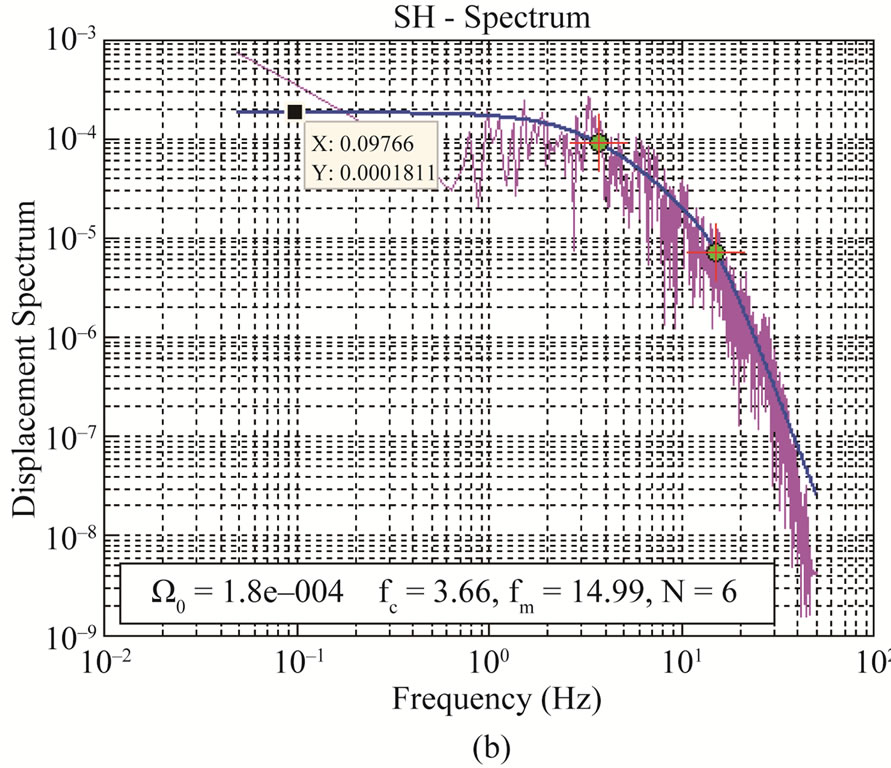
Figure 4. Plot (a) acceleration spectrum for estimation of AIFL and (b) displacement spectrum for estimation of Ω0.
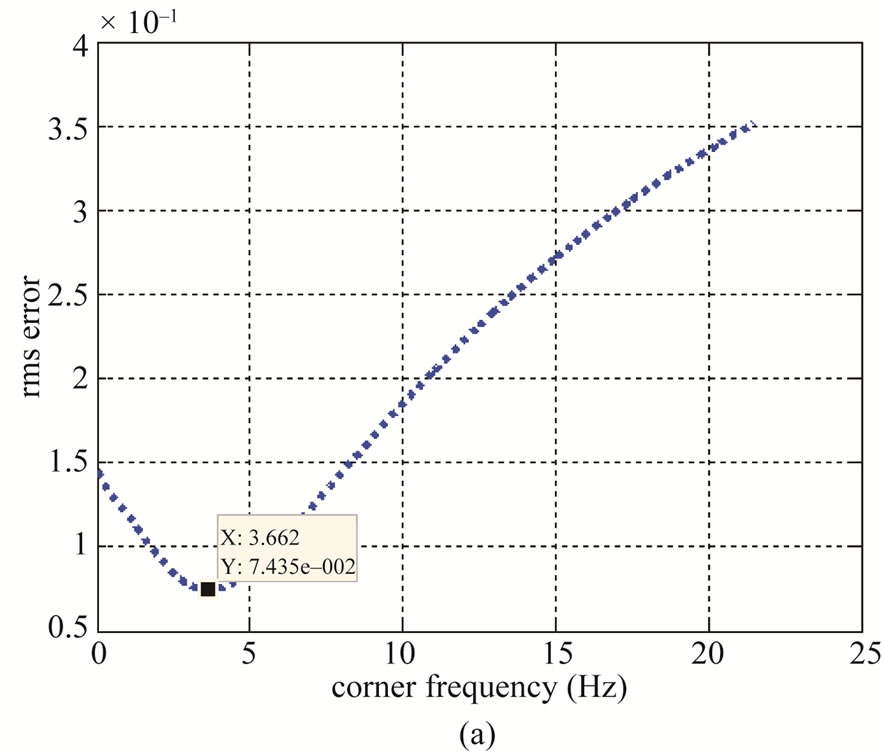
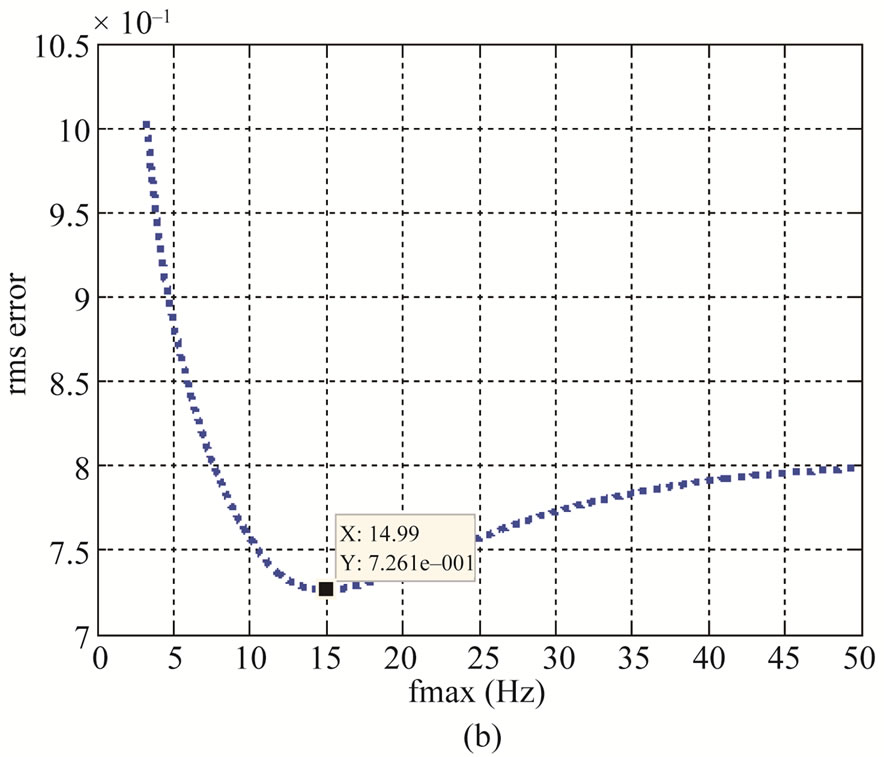
Figure 5. Plot of rms error and (a) corner frequency (b) fmax. Values with least rms error are shown for fc and fmax in respective plots.
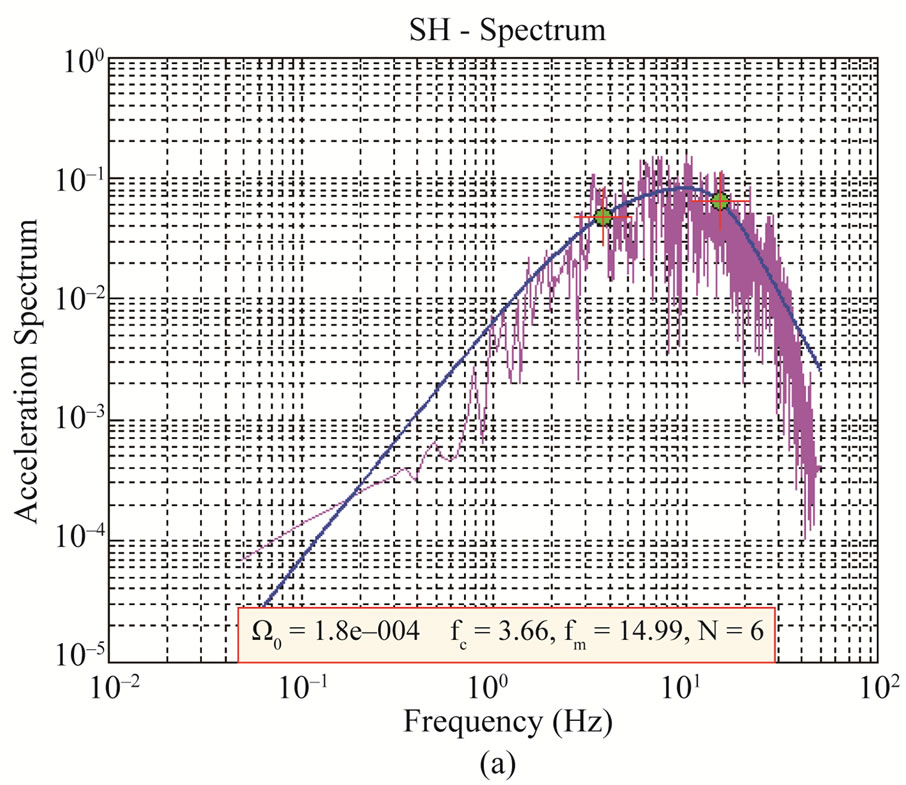
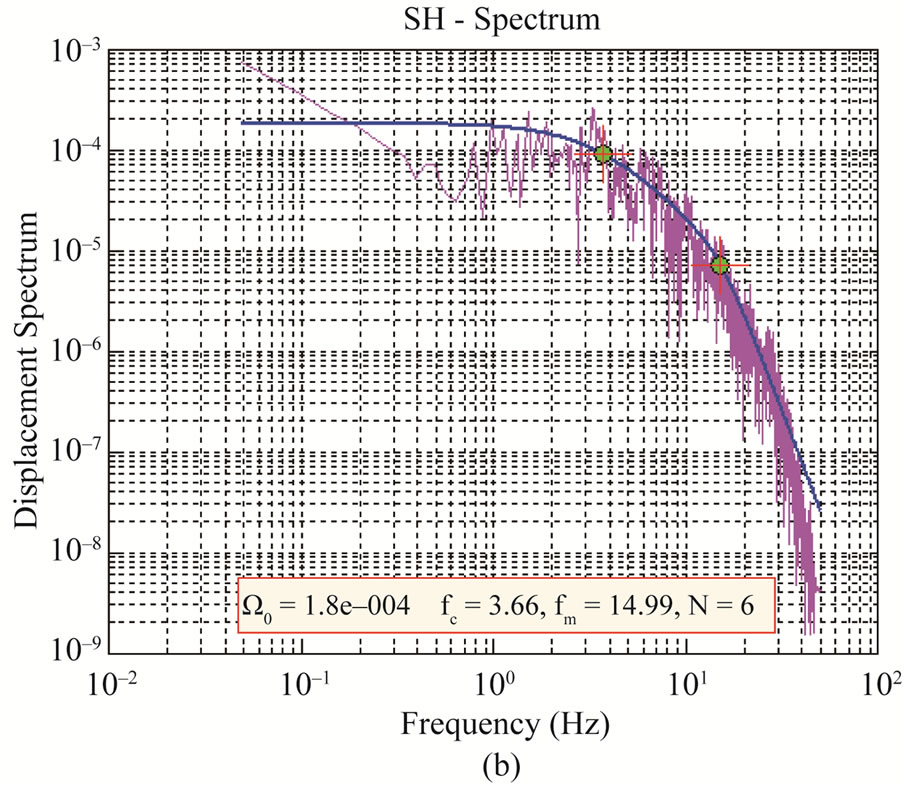
Figure 6. Plot (a) acceleration spectrum and (b) displament spectrum along with fitted source model from finally obtained spectral values.
the value of N having least difference between the considered model and observed spectrum is obtained (Figure 6).
A flowchart of the procedure is given in Figure 7.
The seismic moment is estimated from the value of Ω0 following Kellis-Borok [27] as:
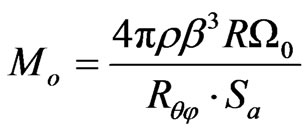 (5)
(5)
Here 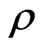 is the average density (=2.67 g/cm3),
is the average density (=2.67 g/cm3), 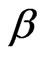 is shear wave velocity in the source zone (=3.2 km/s),
is shear wave velocity in the source zone (=3.2 km/s), 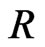 is the hypocentral distance,
is the hypocentral distance, 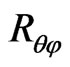 is the average radiation pattern (=0.63),
is the average radiation pattern (=0.63), 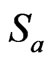 is free surface amplification (=2).
is free surface amplification (=2).
The moment magnitude is obtained following Hanks and Kanamori [28] as:
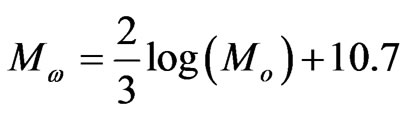 (6)
(6)
Following Brune [1,2] the source radius and stress drop can be estimated as:
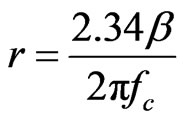 (7)
(7)
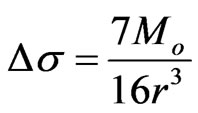 (8)
(8)
3. Estimation of Source Parameters
The data collected from two networks in the Garhwal Himalaya (Figure 8): Strong motion network (GSR-18, sampling rate 200 Hz) available on www.pesmos.in [29] and 12-stations seismological network (Guralp, CMG 40T-1, sampling rate 100 Hz) has been used for estimation of source parameters. Figures 9 and 10 show the rotated time histories and the selected part of SH-com-
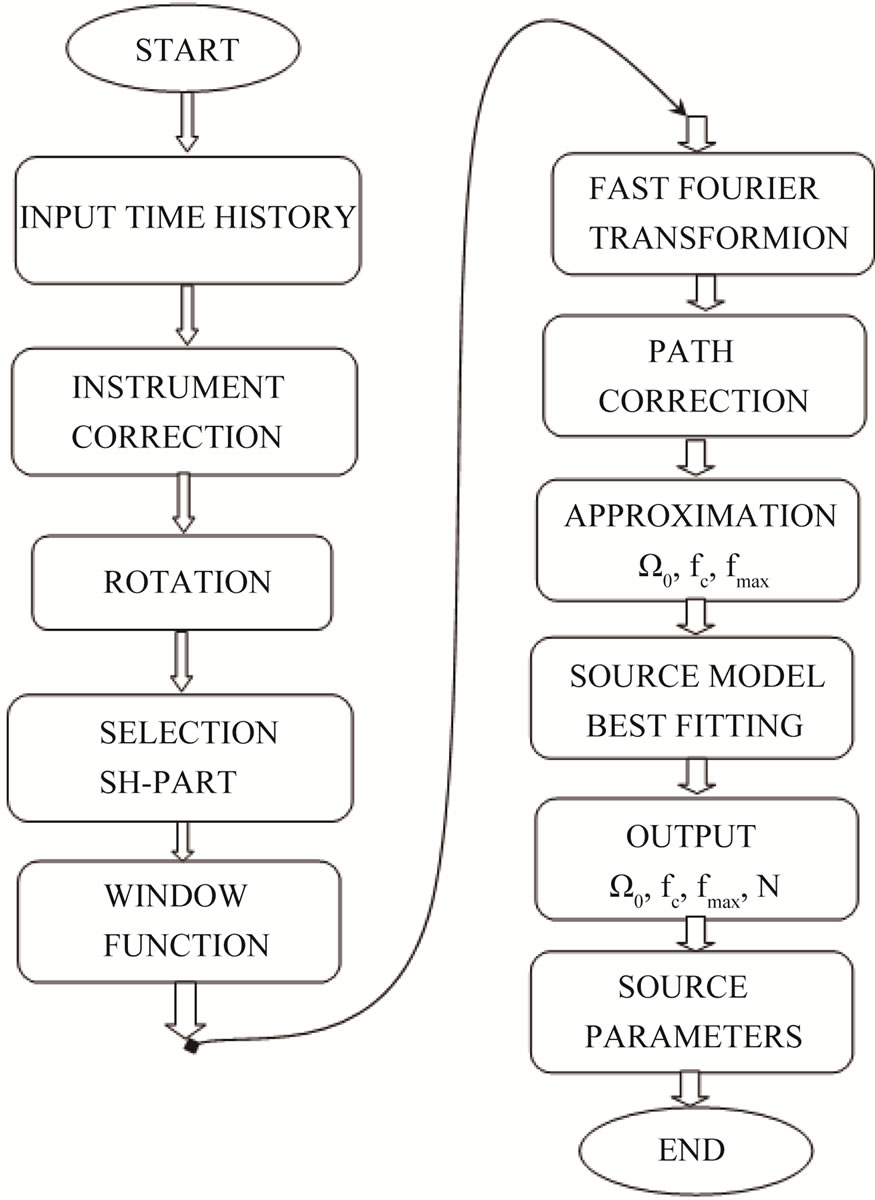
Figure 7. Flowchart of procedure adopted for estimation of earthquake source parameters.
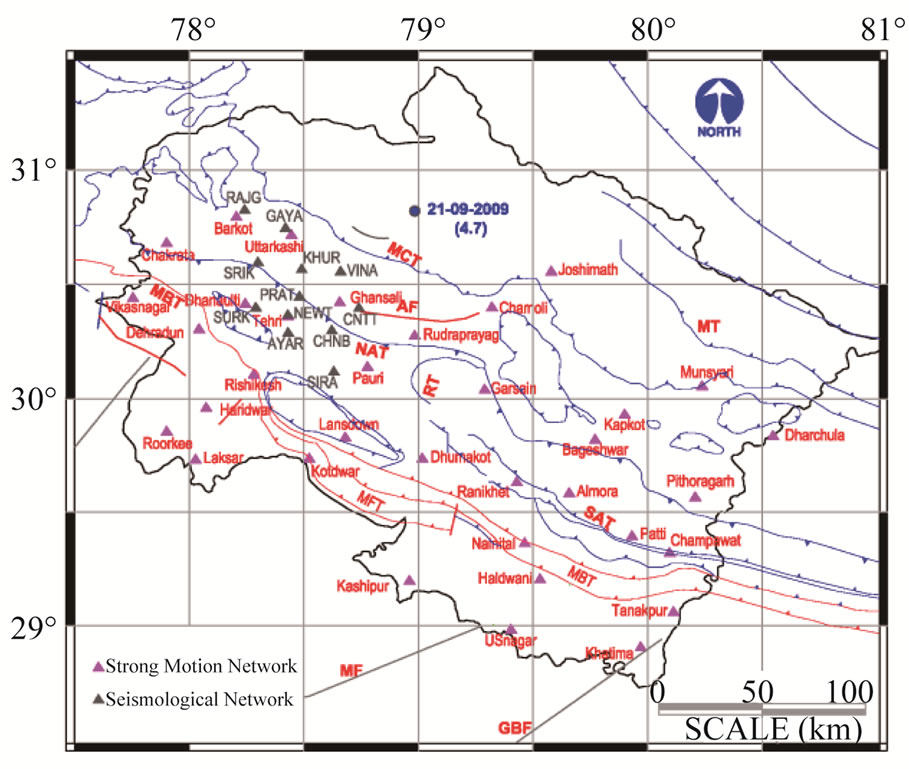
Figure 8. Seismotectonic map of Uttrakhand (tectonics after GSI [30]) along with the location of instruments, strong motion (mangenta triangles) and short period (black traingles). The location of earthquake of 21st September 2009 (Mw 4.7) is shown by blue circle.
ponent used for analysis from seismogram (Vinakhal) and strong motion instrument (Dhanolti). The acceleration and displacement spectra along with the fitted model are also shown below in respective figures.
The spectral parameters obtained from the velocity and acceleration records at various sites are given along with
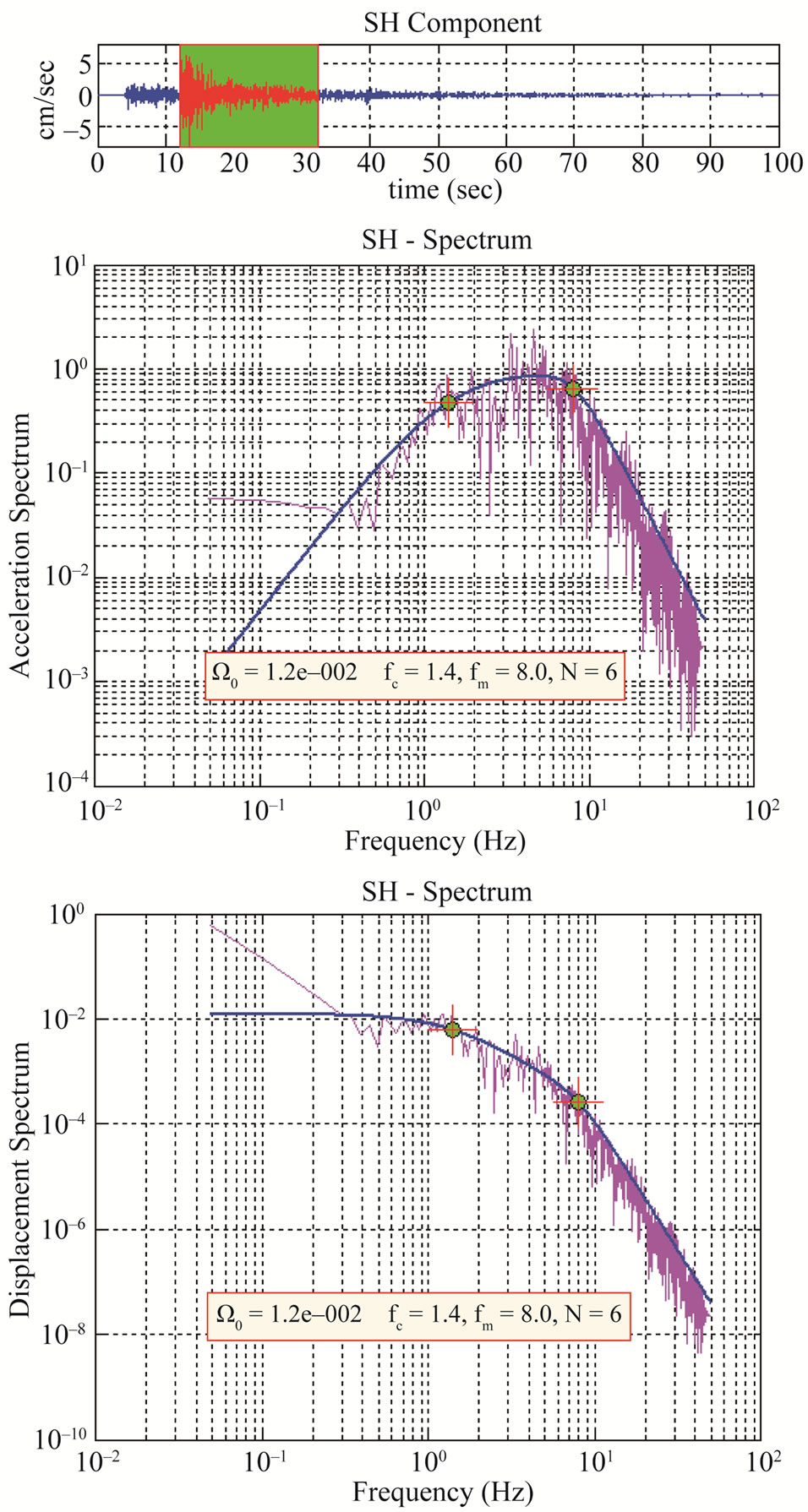
Figure 9. An example of SH component of time history of earthquake recorded at Vinakhal on short period seismograph.The acceleration and displament spectra along with fitted source model are shown in bottom.
estimated source parameters in Appendix 1.
The seismic moment for this event has been found to be of the order of (107 ± 0.19) × 1023 dyne.cm and the moment magnitude has been calculated 4.7 ± 0.09 at different stations. The stress drop is found to be 76.3 ± 11.5 bars, while source radius for the earthquake is estimated to be (850.0 ± 38.0) m. The value of fmax for this earthquake is 9.1 ± 1.7 Hz obtained from records at various stations of different site conditions. A change in spectral fall-off above fmax has been observed in short period instruments while strong motion instruments has same value. This may be due to different band-width of recording instruments.
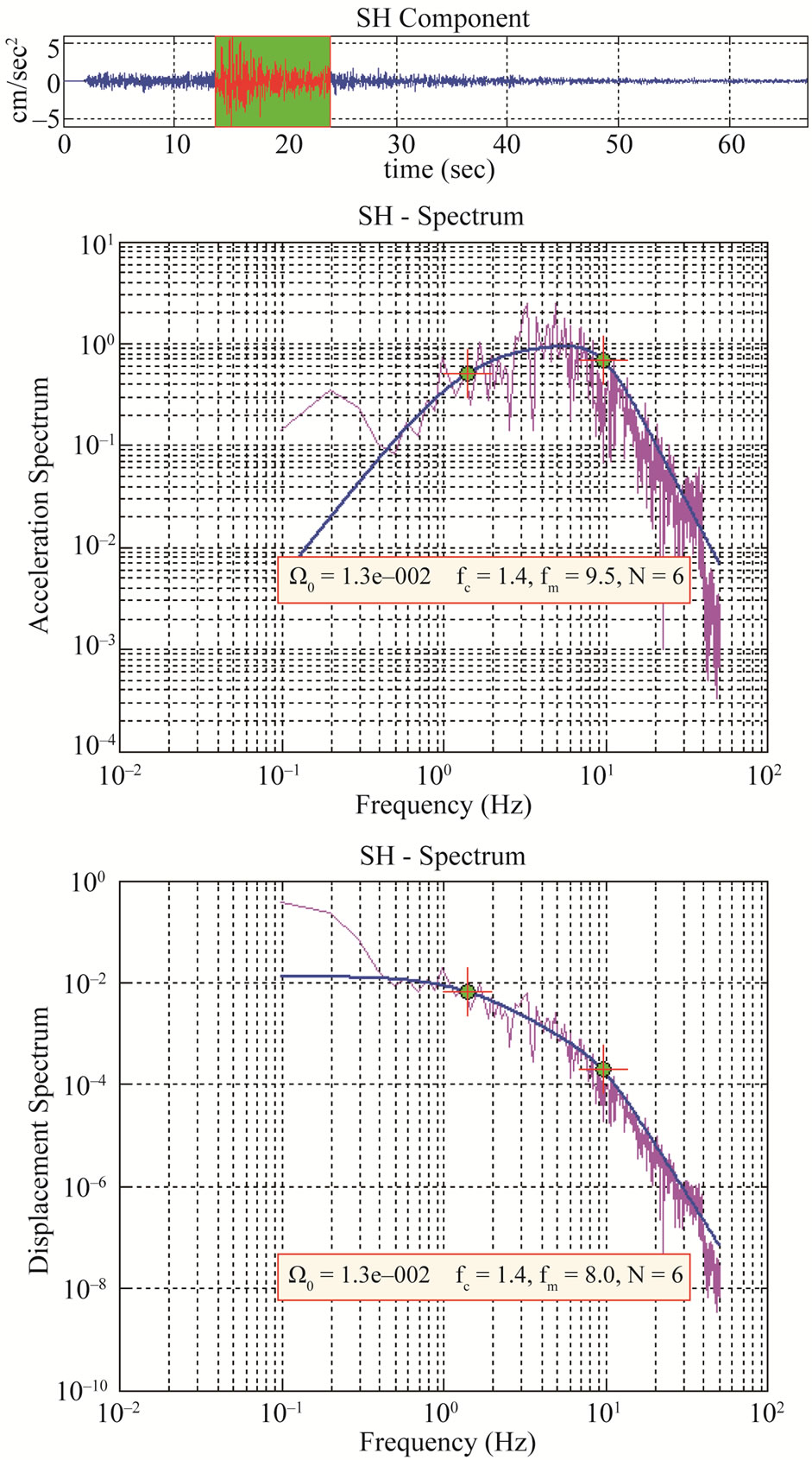
Figure 10. An example of SH component of acceleration time history of earthquake recorded at Dhanolti on strong motion instrument. The acceleration and displament spectra along with fitted source model.
4. Conclusions
The software EQK_SRC_PARA has been written in MATLAB and is based on Brune’s source model (1970) and high cut-off frequency factor of Boore (1983). It uses input data in Sesame ASCII Format (SAF) format. The software automatically picks the spectral parameters: low frequency displacement spectral level (Ω0), corner frequency above which spectrum decays with a rate of 2 (fc), the cut-off frequency above which the spectrum again decays (fmax) and the rate of decay above fmax (N). The obtained spectral parameters have been used to estimate source parameters (e.g., seismic moment, source dimension and stress drop etc.) and to develop scaling laws. The cut-off frequency “fmax” can also be studied and interpreted to find clues about its origin.
The estimated stress drop for this event is 76.3 ± 11.5 bars that is higher than the stress drop of 52.6 ± 5.9 bars for Uttarkashi earthquake (Mw 6.7) of 1991 and an average of about 60 bars for Garhwal-Kumaon Himalayan earthquakes (Kumar, 2011). The difference in focal depth may be the cause of higher stress drop in this earthquake.
5. Acknowledgements
The author (Arjun Kumar) is profusely thankful to Ministry of Human Resources Development (MHRD) for providing fellowship. The authors are also thankful to Ministry of Earth Sciences (MoES) and Tehri Hydropower Development Corporation (THDC) for funding projects under which data was collected.
REFERENCES
- J. N. Brune, “Tectonic Stress and the Spectra of Seismic Shear Waves from Earthquakes,” Journal of Geophysical Research, Vol. 75, No. 26, 1970, pp. 4997-5009. doi:10.1029/JB075i026p04997
- J. N. Brune, “Correction to Tectonic Stress and the Spectra of Seismic Shear Waves from Earthquakes,” Journal of Geophysical Research, Vol. 76, No. 20, 1971, p. 5002. doi:10.1029/JB076i020p05002
- D. M. Boore, “Stochastic Simulation of High-Frequency Ground Motion Based on Seismological Models of the Radiated Spectra,” Bulletin of the Seismological Society of America, Vol. 73, No. 6, 1983, pp. 1865-1894.
- W. S. Joyner, “A Scaling Law for the Spectra of Large Earthquakes,” Bulletin of the Seismological Society of America, Vol. 74, No. 4, 1984, pp. 1167-1188.
- K. Aki, “Scaling Law of Seismic Spectrum,” Journal of Geophysical Research, Vol. 72, No. 4, 1967, pp. 1217- 1231. doi:10.1029/JZ072i004p01217
- B. E. Tucker and J. N. Brune “Source Mechanism and Mb-Ms Analysis of Aftershocks of the San Fernando Earthquake,” Geophysical Journal. Royal Astronomical Society, Vol. 49, No. 2, 1977, pp. 371-426. doi:10.1111/j.1365-246X.1977.tb03714.x
- J. B. Fletcher, “Spectra from High Dynamic Range Digital Recordings of Oroville, California, Aftershocks and Their Parameters,” Bulletin of the Seismological Society of America, Vol. 70, No. 3, 1980, pp. 735-755.
- R. J. Archuleta, E. Cranswick, C. Mueller and P. Spudish, “Source Parameters of the 1980 Mammoth Lakes, California, Earthquake Sequence,” Journal of Geophysical Research, Vol. 87, No. 12, 1982, pp. 4595-4607. doi:10.1029/JB087iB06p04595
- M. L. Sharma and H. R. Wason, “Occurrence of Low Stress Drop Earthquakes in the Garwal Himalayan Region,” Physics of the Earth and Plantary Interiors, Vol. 85, No. 3-4, 1994, pp. 265-272. doi:10.1016/0031-9201(94)90117-1
- A. Kumar, A. D. Pandey, M. L. Sharma, S. C. Gupta, A. K. Verma and B. K. Gupta, “Processing and Preliminary Interpretation of Digital Data Obtained from Digital Telemetered Seismic Array in the Garhwal Himalaya,” Xth Symposium on Earthquake Engineering, University of Roorkee, Roorkee, 1994.
- B. K. Bansal, “Determination of Source Parameters for Small Earthquake in the Koyna Region,” 11th Symposium on Earthquake Engineering, Roorkee, 15 May-10 July 1998, pp. 57-66.
- A. Kumar, “Study of Earthquake Source Parameters Using Microearthquakes and Strong Motion Data,” Indian Institute of Technology, Roorkee, 2011.
- T. C. Hanks, “fmax,” Bulletin of the Seismological Society of America, Vol. 72, 1982, pp. 1869-1879.
- J. G. Anderson and S. E. Hough, “A Model for the Shape of the Fourier Amplitude Spectrum of Acceleration at High Frequencies,” Bulletin of the Seismological Society of America, Vol. 74, No. 5, 1984, pp. 1969-1993.
- A. S. Papageorgiou and K. Aki, “A Specific Barrier Model for the Quantitative Description of Inhomogeneous Faulting and the Prediction of Strong around Motion. I. Description of the Model,” Bulletin of the Seismological Society of America, Vol. 73, No. 3, 1983, pp. 693-722.
- A. S. Papageorgiou and K. Aki, “A Specific Barrier Model for the Quantitative Description of Inhomogeneous Faulting and the Prediction of Strong ground Motion. I1. Application of the Model,” Bulletin of the Seismological Society of America, Vol. 73, No. 4, 1983, pp. 953-978.
- E. Faccioli, “A Study of Spectra and Peak Values of Strong Motion Accelerograms from Italy and Yugoslavia in Terms of Gross Source Properties,” In: S. Das, J. Boatwright and C. H. Scholz, Eds., Earthquake Source Mechanics, Geophysical Monograph 37, Maurice Ewing Series, American Geophysical Union, Washington, 1986, pp. 297-310. doi:10.1029/GM037p0297
- K. Aki, “Magnitude-Frequency Relation for Small Earthquakes: A Clue to the Origin of fmax of Large Earthquakes,” Journal of Geophysical Research, Vol. 92, No. B2, 1987, pp. 1349-1355. doi:10.1029/JB092iB02p01349
- A. S. Papageorgiou, “On Two Characteristic Frequencies of Acceleration Spectra: Patch Corner Frequency and fmax,” Bulletin of the Seismological Society of America, Vol. 78, No. 2, 1988, pp. 509-529.
- Y. Toshiaki and K. Irikura, “Meaning of Source Controlled fmax in Empirical Green’s Function Technique Based on a T2-Scaling Law,” Disaster Prevention Research Institute, Kyoto University, 1991.
- S. Kinoshita, “Local Characteristics of the fmax of Bedrock Motion in the Tokyo Metropolitan Area, Japan,” Journal of Physics of the Earth, Vol. 40, No. 3, 1992, pp. 487-515. doi:10.4294/jpe1952.40.487
- M. Tsurugi, M. Tai, A. Kowada, Y. Tatsumi and K. Irikura, “Estimation of Empirical Site Amplification Effects Using Observed Records,” 12 World Conferenc on Earquake Engineering, Auckland, 30 January-4 Febuary 2000, pp. 1-6.
- M. Tsurugi, T. Kagawa and K. Irikura, “Study on High- Cut Frequency Characteristics of Ground Motions for Inland Crustal Earthquakes in Japan,” 14 World Conferenc on Earquake Engineering, Beijing, 12-17 October 2008, No. 02-0036.
- J. Wen and X. Chen, “Variations in fmax along the Ruptured Fault during the Mw 7.9 Wenchaun Earthquake of 12 May 2008,” Bulletin of the Seismological Society of America, Vol. 102, No. 3, 2012, pp. 991-998. doi:10.1785/0120110105
- S. C. Gupta and A. Kumar, “Seismic Wave Attenuation Characteristics of Three Indian Regions: A Comparative Study,” Current Science, Vol. 82, No. 4, 2002, pp. 407- 413.
- G. Glassmoyer and R. D. Borcherdt, “Source Parameters and Effects of Bandwidth and Local Geology on HighFrequency Ground Motions Observed for Aftershocks of the Northeastern Ohio Earthquake of 31 January 1986,” Bulletin of the Seismological Society of America, Vol. 80, No. 4, 1990, pp. 889-912.
- V. I. Keilis-Borok, “Investigation of the Mechanism of Earthquakes,” Bulletin of the Seismological Society of America, Vol. 51, No. 1, 1961, p. 132.
- T. C. Hanks and H. Kanamori, “A Moment Magnitude Scale,” Journal of Geophysical Research, Vol. 84, No. B5, 1979, pp. 2348-2350. doi:10.1029/JB084iB05p02348
- A. Kumar, H. Mittal, R. Sachdeva and A. Kumar, “Indian National Strong Motion Network,” Seismological Research Letters, Vol. 83, No. 1, 2012, pp. 29-36. doi:10.1785/gssrl.83.1.59
- GSI, “Seismotectonic Atlas of India and Its Environs,” Geological Survey of India publication, Kolkata, 2000.
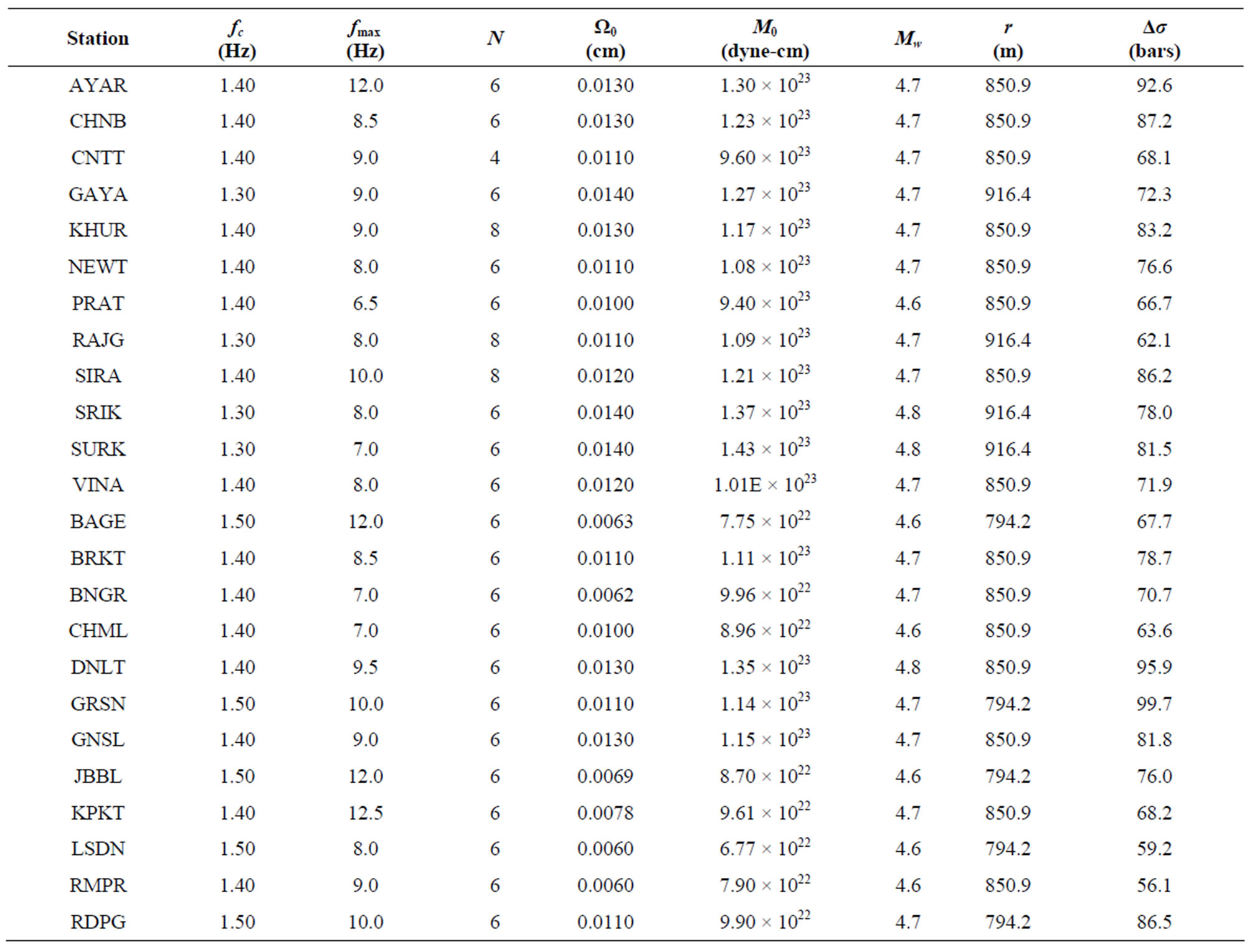
Appendix 1. Spectral parameters and the estimated source parameters of 21/09/2009 earthquake.
NOTES
*Corresponding author.

