Received 11 September 2014; revised 10 October 2014; accepted 2 November 2014

ABSTRACT

The relative contribution of long-distance dispersal and local diffusion in the spread of invasive species has been a subject of much debate. Invasion of the intertidal mudflats by Spartina alterniflora is an ideal example of stratified diffusion, involving both long-distance dispersal of seeds and local diffusion due to clonal growth. In conjunction with experimental data on range radius-ver- sus-time curve, a traveling wave equation-based model is used to investigate the sensitivity of the spread rate of exotic S. alterniflora to parameters of long distance dispersal (c, maximum colonial establishment rate) and local colony diffusion (r, intrinsic growth rate) at two tidal marshes, the Eastern Chongming and the Jiuduansha Islands, at the Yangtze River estuary. Both Eastern Chong ming and Jiuduansha Islands are now national natural reserves in China, which were established in 2005. However, the mudflats and salt marshes in the two reserves are now heavily infested with introduced S. alterniflora, which may threaten the estuarine ecosystems and their biodiversity. S. alterniflora was first found in 1995 on Chongming. For rapid sediment accretion in mudflats in the estuary, S. alterniflora was also intentionally introduced to Jiuduansha in 1997 and Chongming in 2001, which has led to a rapid range expansion in the estuary. Our results show that range expansion of species with stratified diffusion is affected by both long-distance dispersal and local colony diffusion, and that there is a critical c^*, below which the spread rate is more influenced by long- distance dispersal than by local diffusion. After applying this model to the invasion of S. alterniflora in the Yangtze River estuary, we derive that c = 1.7 × 10⁻³, c^* = 0.126 and c = 4.8 × 10⁻³ km⁻²∙yr⁻¹, c^* = 0.140 km⁻²∙yr⁻¹ at Chongming and Jiuduansha (Shanghai), respectively. Our results suggest that the range spread of S. alterniflora in the Yangtze River estuary is more influenced by long- distance dispersal than local colony diffusion, and that S. alterniflora generates about 1.7 × 10⁻³ to 4.8 × 10⁻³ colonies per square kilometers per year. This study provides important information about dispersal dynamics of S. alterniflora that may be useful for finding optimal control strategies.

Keywords:

Long-Distance Dispersal, Stratified Diffusion, Sensitivity Analysis, Traveling Wave Equation, Spartina alterniflora

1. Introduction

Like other complex biological processes, the expanding process of invasive species is often numerically intractable [1] - [5] . The study of spread rates of invasions has been and continues to be one of the most exciting areas of interplay between theoretical and observational study in ecology [2] .

Early models of the spread of animal and plant populations were based on the process of diffusion and predicted a simple linear rate of spread [2] [6] [7] . However, empirical patterns of spread for some species are nonlinear [2] . For example, in a review of 14 invasive plants, seven showed linear spread and seven exponential spread [8] . In some cases, invasive species have both a long-distance dispersal (i.e., leads to establishment of offspring far from parents) and a local reproduction (by which colonies increase in local density) [9] . A combination of different dispersal scales is called stratified diffusion [9] . For stratified diffusions, various types of range expansion (i.e., different range-time curves) depends substantially on how and where short and long-dis- tance dispersers are produced and what distances they move [9] .

For many invading species, the key to understanding the expanding process is ascertaining rare long-distance dispersal events, such as the movement of Argentine ants and Phytophthora lateralis disease spores by cars and trucks, or of zebra mussels by boats [10] - [12] . Ignoring these rare long-distance dispersal processes can lead to significant underestimates of range expansion of invasive species [2] . However, the relative contribution of long-distance dispersal vs. local growth in the spread of invaders is poorly understood and remains a subject of active debate [2] [3] [13] [14] . In addition, while dispersal patterns have been studied for many species, either as seed shadows, plant-disease dispersal gradients, or mark-recapture data, the empirical estimation of rare long- distance dispersal events at larger scales is still one of the major challenges to ecology [2] .

Spread models can be used to explore these two issues of ecology [2] . For example, the main use of spread models has been to predict the velocity of the invasion front from species attributes related to reproduction and dispersal, thus we can explore the relative importance of dispersal and local growth in contributing to the spread rate by comparing the partial derivatives of spread rate with respect to dispersal and reproduction parameters, respectively. On the other hand, we can fit the dispersal parameters (or testing hypotheses about dispersal mechanisms) if we can estimate the reproduction parameter and have known the rates of spread by field mapping of an invasion front over successive years or using time series data of aerial photos [5] [15] - [17]

Invasion of the intertidal mudflats of Pacific coast estuaries by Spartina alterniflora Loisel. (smooth cordgrass) is an ideal example of stratified diffusion, involving both a long-distance dispersal of seeds that leads to establishment of new colonies and a local reproduction due to clonal growth through rhizome [17] [18] . The result over time is a moving of growing patches: earlier invaded areas have relatively larger and denser patches and newly invaded areas have smaller and sparser patches (Figure 1). The relevant questions are: which process play more important role in the range spread of S. alterniflora, long-distance dispersal of seeds or local clonal growth? How to estimate of the long-distance dispersal coefficient of this species at larger scales? This knowledge is quite necessary and critical in finding optical control strategies for this species [19] [20] .

In this study, we apply the concept of stratified diffusion to model the spread of exotic S. alterniflora and then fit the dispersal coefficient of S. alterniflora using aerial photographs data on range radius-versus-time curve of S. alterniflora at two tidal marshes on Chongming Island and Jiuduansha Islands respectively at the Yangtze River estuary for a period of nine to ten years after introduction in this area.

Like other estuaries, the Yangtze River estuary is an important ecoregion, because it provides great ecosystem services for humans and wildlife in the region. Maintaining the integrity of the native ecosystems and conserving biodiversity in this estuary is of national importance. Therefore, two national reserves were established in 2005 in the estuary, one on Chongming Island and the other on Jiuduansha Islands (see Figure 1 in [21] ). However, the mudflats and salt marshes in the two reserves are now heavily infested with introduced S. alterniflora, which may threaten the estuarine ecosystems and their biodiversity. S. alterniflora was first found in 1995 ion Chongming Island in the Yangtze River estuary and is believed to have arrived there though natural dispersal by water flow from Qidong, Jiangsu Province. For rapid sediment accretion in mudflats in the estuary, S. alterniflora was intentionally introduced to Jiuduansha in 1997 and Chongming in 2001 (Figure 1(A)), which has led to a rapid range expansion in the estuary. Chongming Island is the largest (the third largest in China the largest alluvial island in the world); and Jiuduansha Islands, consisting of three islands, are the youngest, first emerging in 1954.

The introduction of S. alterniflora to the tidal marshes on Chongming and Jiuduansha at the Yangtze River estuary is a prime example of a spatially structured invasion, for which model performance can be assessed against the actual survey of population spread. In particular, the stratified diffusion model is constructed so that the relative effects of dispersal and local growth on the range expansion can be explicitly modeled.

2. Methods

2.1. Species and Dispersal Characteristics

Spartina alterniflora was deliberately introduced from the Atlantic coast of North America into China in 1979 to check erosion and promote sediment accretion. Although S. alterniflora still exhibits some anticipated ecological benefits [19] [21] , it has become an invasive and damaging ecosystem engineer in many coastal wetlands in China [21] .

Invasion of the intertidal mudflats of estuaries by S. alterniflora is a primary example of a stratified diffusion in a relatively simple habitat [22] [23] . Its long distance dispersal along a tidal elevation gradient was driven primarily by seedling recruitment [1] [24] [25] . Following initial colonization, spatially round clonal patches dot the mudflats and grow vegetatively through rhizomes [17] [26] [27] . Eventually they coalesce to form expansive meadows (Figure 1). The upper tide zone tends to be invaded first because it is more favorable for seedling establishment [24] . Over time, plants establish further out from shore as growing upper tidal meadows serve as a source of seeds [24] .

2.2. Model Assumptions and Structure

The model used here is almost identical to the one used by [28] and has been described into detail by them. We only provide a short description here. We consider the following two zones at the moving population front of S. alterniflora (Figure 1): 1) the meadow edge zone that is assumed to be a main source of long-distance dispersal; 2) the transition zone where new clonal patches become established. New local patches become established at varying distances from the wave front, which is the boundary between the dense meadow and the transition zones. We assume that the wave front is a straight line that progresses uniformly at all locations. Thus, we can build the model using just one spatial coordinate (also along the tidal elevation gradient from upper to lower mudflats) that is perpendicular to the population front.

Our objective is to calculate the rate of population spread from the following two functions: 1) patch establishment rate (per unit area per year), b(x), which continuously decreases with increasing distance from the wave front, x, a pattern consistent with aerial photo analysis by previous studies [5] [17] [27] ; 2) increase of ramet density of a patch, n(a), which continuously increases with clone age (time since colonization), a.

It is worth noting for these model assumptions: First, the model describes the average density (ramets per unit area) of S. alterniflora, m (a, z, t), of age a, at spatial location z, and at time t. Although natural extinction of colonies did occur, we ignored it in the model by considering only those patches that successfully established. This may make the patch establishment rate, b(x), smaller. Second, by definition, the wave front is located at the point where the average ramet density is approximate to carrying capacity, K. We do not use parameter K to limit the growth of individual patches because we intend to simulate population dynamics only in the transition zone where the average ramet density is below the carrying capacity. Third, the simplified assumption that the patch establishment rate depends only on the distance from the population front does not imply that all long-distance dispersal originates only from the wave front. Usually, isolated patches in the transition zone have low densities. Thus, their contribution to long-distance dispersal should be much smaller than the contribution of high-density populations that have reached the carrying capacity (e.g. plants in the meadow edge zone, Figure 1).

Thus, the following traveling wave equation can be used for estimating the spread rate of the front, v, if functions b(x) and n(a) are specified explicitly [28] ,

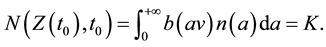(1)

We assume that the ramets density of a patch, n(a), increases exponentially with colony age a,

, (2)

where n₀ is the number of initial ramets of S. alterniflora in a patch, and r is the intrinsic growth rate.

Dispersal data are frequently fit with a negative exponential curve or a negative power function [29] . As a reasonable simplifying, we give three types of negative functions of b(x) below:

1) Constant decreasing function

We suppose that b(x) decrease linearly with the distance x, namely,

, (3)

where x_max is the maximum distance at which the patch of S. alterniflora could establish (namely, the width of the transition zone) and c = b(0) > 0, is the dispersal coefficient, the maximum patch establishment rate in the transition zone. Equation (1) yields the following equation,

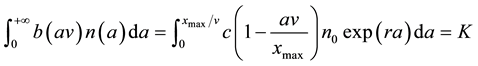, (4)

namely,

, (5)

where V = v/x_max, the relative rate of population spread (proportional to the width of the transition zone, x_max). Thus we can use numerical method to estimate V.

2) Decelerated decreasing function

We suppose that the establishment rate of new colony decelerates decreases with the distance away from the front, namely,

(6)

And we obtain the traveling wave equation as follows,

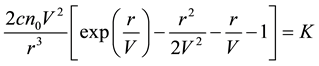. (7)

3) Accelerated decreasing function

We suppose that the establishment rate of new colony accelerates decreases with the distance away from the front, namely,

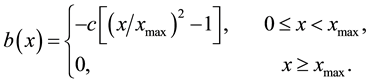(8)

Similarly, we obtain the traveling wave equation as following,

. (9)

The model did not differ qualitatively in behavior when each of the three functions of b(x) was chosen (Figure 3). Therefore, we use the constant decreasing function of b(x) to construct our model.

2.3. Model Analysis

The spread rate of the front depends mainly on parameter c and r (Equation (5)). We cannot solve the Equation (5) analytically, and thus use numerical methods to analyze. The values of n₀/K quantify the initial density of individuals in the transition zone. We expect this value to be very small (<0.01) in most local populations, because establishment of new colonies is a rare event on tidal mudflats and the initial number of individuals is usually small [17] . We calculated the partial derivatives of V with respect to r and c to explore the relative importance of dispersal and local growth in contributing to the spread rate.

2.3.1. Fitting Dispersal Parameter from the Range-Time Curves

We used available data on the range spread of S. alterniflora from two sites in the Yangtze River estuary: Jiuduansha Shoals Wetlands (30˚10'N, 122˚01'E) and Chongming Dongtan Wetlands (31˚38'N, 121˚58'E) [5] [17] . In these studies, estimates of area changes of S. alterniflora with time were taken from aerial photographs. We used the changes in range as estimations of spread rate of v. Simple lineal models predict the spread rate of S. alterniflora to be constant over time (Figure 2). In order to apply our model to the fitting of dispersal parameter c of S. alterniflora in the Yangtze River estuary, we make the following estimates of other model parameters (Table 1):

Parameter x_max: the mean maximum distance from the wave front where isolated colonies become established.

This distance has been reported to be a maximum about 2 km based on aerial photographs take in the Yangtze River estuary [17] . Due to the proportional effect of x_max on the rate of spread, we assumed that x_max = 2000 m.

Parameter n₀: the initial number of established seedlings in isolated populations. We assumed that a colony may start from a small number of seedlings (<10) based on the observation of widely scattered distribution of seedlings (not tightly clumped). Three levels of n₀ were initially tested within a reasonable range (1, 3and 10). Due to the similarity in the outcome, only results for n₀ = 3 are presented.

Parameter K: carrying capacity. In this paper, we use mean ramet density in meadow as an estimation of K for S. alterniflora in the Yangtze River estuary. The value has been reported to be 262 ramet m⁻² [30] . Thus, we assumed K = 262 ramet m⁻².

Parameter r: the rate of ramet number increasing with colonies. Some studies estimated the average intrinsic rate of increase in S. alterniflora colonies from samples collected in several sites in the Yangtze River estuary [31] . The average intrinsic rate of population increase was r = 1.57. In the model, we assumed the value r = 1.5.

2.3.2. Model Accuracy Assessment

In this study the velocity of spread has been estimated from time series of aerial photos [5] [17] . Thus the dispersal coefficient (c) could be determined by simulation to accommodate unique combinations of the r and the rate of spread. Meanwhile, we also estimate the dispersal coefficient (c) by a coalescing colony model which has been suggested by [9] . Thus, we define the derivation (or match) of estimated c between from our model and the coalescing colony model as the accuracy (expressed in percentage) assessment of our model.

3. Results and Discussion

The relative spread rate V almost increased linearly with parameter r and c respectively (Figure 3). There was a critical dispersal rate c^* in the sensitivity analysis (Figure 4): when c < c^*, the parameter c played a more important role in the relative spread rate than r (dV/dc > dV/dr); when c > c^*, r weighted more than the parameter c on spread rate (dV/dc < dV/dr). In this study, the fitted values of c = 1.7 × 10⁻³ and 4.8 × 10⁻³ km⁻²∙yr⁻¹, and c^* = 0.126 and 0.140 km⁻²∙yr⁻¹ at Chongming and Jiuduansha, respectively. More generally, within a biologically reasonable scope of parameter r (0.5 - 1.5) for S. alterniflora, the values of the critical dispersal coefficient (c^*) were far below 1 (Figure 4), indicating the estimated c is smaller than its corresponding c^* by approximately three orders of magnitude. Thus, we suggest that the range spread of S. alterniflora in the Yangtze River estuary

is more influenced by long-distance dispersal than local growth. Our results support the proposal that, for species that spread through stratified diffusion, the distance and rate at which new foci are created may be more important than the rate of spread through local diffusion from established foci [9] . For example, using simulations demonstrated that long-distance dispersal by as little as 0.001% could increase predicted rate of spread by an order of magnitude [4] .

For both Chongming and Jiuduansha, range expansion of S. alterniflora was linear (Figure 2). To account for this observed pattern through a coalescing colony model of stratified diffusion [9] , the estimated c was about 6.1 × 10⁻³ and 6.3 × 10⁻³ km⁻²∙yr⁻¹ at Chongming and Jiuduansha, respectively. The accuracy was 28% and 76% respectively. The range of predictions made by our model and coalescing colony model of stratified diffusion has the same order of magnitude [9] . Thus, the dispersal coefficients predicted by this study are quite reasonable. Long-distance jump-dispersal events are believed to be rare and difficult to measure [2] . Our result confirms the proposal that, by determining the spread rate and local growth parameter, we can fit the dispersal parameters using spread models of invasive organisms [2] .

The extent to which species spread by stratified diffusion may influence the implementation of control strategies. For example, the effectiveness of control measures can be greatly increased by preventing the establishment of new foci or by eliminating new foci rather than focusing efforts on established invasion fronts [22] [23] [28] [32] . As demonstrated in this study, the establishment of new foci through long-distance dispersal is of paramount importance in the spread of S. alterniflora and control efforts should be placed on the transition zone, and focus on preventing the dispersal processes and slowing the advancing wave fronts. Thus, some measures can be taken, such as arranging a barrier in the transition zone to slow the spread of S. alterniflora [28] . Currently, a demonstration project is being carried out in the Yangtze River Estuary, in which integrated a dam building and an integrated approach of clipping, water logging and ecological replacement with reed are being attempted [20] , based on the control strategies drawn from this study.

Acknowledgements

We are grateful to Prof. Cangming Fang, Hanji Shang, and Bing Zhao for constructive comments on the earlier versions of this manuscript. This study was financially supported by the National Natural Science Foundation of China (31370433) and the National Basic Research Program (Grant No. 2006CB403305).

References

Appendix

Based on the traveling wave Equation (5), the derivatives of V with respect to r and c are given as following.

, (10)

. (11)

NOTES

^*Corresponding author.