American Journal of Plant Sciences
Vol.05 No.20(2014), Article ID:50176,16 pages
10.4236/ajps.2014.520320
Canopy storage implications on interception loss modeling
Cesar Véliz-Chávez1, Carlos Alberto Mastachi-Loza2, Enrique González-Sosa3*, Rocio Becerril-Piña2, Norma Maricela Ramos-Salinas4
1Facultad de Ingeniería, Centro Universitario S/N, Cerro de las Campanas, Santiago de Querétaro, Universidad Autónoma de Querétaro, Querétaro, México
2Centro Interamericano de Recursos del Agua, Facultad de Ingeniería Cerro de Coatepec, Ciudad Universitaria, Universidad Autónoma del Estado de México Toluca, Toluca de Lerdo, México
3Departamento de Tecnología Ciencia Arte y Humanidades, Blvd Villas del Meson No. 1000 col. Provincia Juriquilla, Santiago de Querétaro, Universidad del Valle de México Campus Querétaro, Querétaro, México
4División de Estudios de Posgrado, Facultad de Contabilidad y Administración, Universidad Autónoma de Querétaro, Cerro de las Campanas S/N Centro, Querétaro, México
Email: *egs@uaq.mx
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 July 2014; revised 14 August 2014; accepted 10 September 2014
ABSTRACT
A rainfall interception methodology was implemented in a deciduous Ficus benjamina (L.) tree to evaluate the interception loss, as well as the dynamics on canopy storage capacity (S) and free through fall (ρ). Measurements of gross precipitation (Pg), through fall and meteorological data were recorded every 5 minutes. Nineteen individual storms from summer to autumn 2005, and twenty one in spring to autumn, 2006 were analyzed. For the studied period, 151.59 mm and 203.35 mm of rainfall occurred on 2005 and 2006 respectively. Canopy interception was 59.46% and 70.98% of Pg for the first and second year. Throughfall data recorded during 2005 were 38.14% (of Pg) and 27.21% (of Pg) for 2006. The throughfall and gross precipitation relationship yielded S = 1.50 mm for the 2005 data. In 2006 storms were analyzed in detail, where ρ and S varied in a range from 0.10 to 0.64 and from 1.00 to 2.03 mm, respectively. Moreover, application of the Rutter and Gash models with two years of rainfall data (2005-2006) from the study area indicated an underestimation and overestimation of 69% and 88%, respectively. The slightly best prediction of the interception loss was obtained with the Gash model. Yet S and ρ change significantly due to wind speed, temperature, rainfall intensity and seasonal vegetation development.
Keywords:
Interception, storage capacity, throughfall, Gash model

1. Introduction
In urban catchments, the expansion of infrastructure, streets and buildings modify the temperature and humidity of the air, as well as the spatial and temporal distribution of hydrological processes. This is mainly due to the increase of the runoff and pollution by wash-load of streets, which reduce the performance of the storm-water system; therefore, increasing the cost of water treatment. Buildings and urban forests among other urban elements, intercept the precipitation, dropping the volume of runoff. During a rainfall event, each urban element (trees and buildings) plays a different and specify role: 1) buildings intercept and accumulate rainwater on rooftops, which finally falls through the walls to the ground and incorporates into the flow that forms the runoff; 2) rainfall intercepted by canopy trees can be temporarily stored later falling to the ground, or it evaporates directly from the tree surface to the atmosphere [1] , decreasing peak flows and volume of urban runoff. Consequently, urban forests (parks, gardens, isolated trees) can delay the water flow and improve the efficiency to the urban drainage system. For example, it has been found that flooding hazard, surface pollutant wash-off and pollutant loading of the runoff and peak flow all decreased by the rainfall interception of canopy trees [2] . However, the amount of rainfall intercepted by trees is controlled by the canopy density and the rainfall characteristics (i.e. size and type) [1] [3] . Under this consideration, urban parks and urban green areas could be considered as micro catchments that regulate urban moisture. Also in the urban zones, the gradient of temperature can rapidly change, affecting evaporation rates. Moreover, the interception process in urban zones is a very complex issue, since many variables must be taken into consideration, such as spatial location of vegetation, spatial distribution of precipitation, type of constructions, local effects on turbulence, albedo 1 modification, heating effect, and raindrop size distribution. Since Horton’s proposal [4] for individual trees, Rutter et al. [5] and Gash [6] also developed a rainfall interception model considering physical processes. Gash’s analysis is a simplification of the Rutter’s model which incorporates some simple features of the linear regression model within the conceptual background of the Rutter’s model [7] .
During the interception process, there are basically three ways for rainwater to reach the soil surface: 1) rainwater passes through leaves and branches; this portion is known as free throughfall; 2) rainwater flows down the branches and concentrates in the trunk, and later falls down the tree bole; this portion is known as stemflow; and 3) rainwater hits the tree leaves, and during and after the rain event drips down; this portion is known as crown tip or dripping. The sum of free throughfall, stemflow and drip is known as net precipitation. In the three cases, a fraction is evaporated during and after the event, returning to the atmosphere; however, losses in fractions 2) and 3) are less important than losses by interception. At the end of the storm, the rain water stored on the foliage is totally evaporated, and then the canopy is emptied. During each rainfall event, each tree is considered as a mini reservoir, delaying runoff in both, rural and urban zones [2] . The amount of rainfall intercepted by urban trees depends on their spatial location, and species and the architecture of branches and size and form of foliage related to hydrological functionality. Generally, these factors have been studied in forests, stands and isolated trees [1] , and to date, the storage capacity and free throughfall coefficient are the most important parameters for simulation of interception processes. An assortment of these parameters has been obtained from field and laboratory data sets, fitted by regression equations. Analysis of data sets indicated no significant variation, which may be due to the method of derivation; only the species and vegetation cover, and the seasonal change of foliage showed a significant cause (Pipker, 2005) [8] . The storage capacity depends on the temporal and spatial variability of trees, and also the intensity and duration of the storm. Also pruning practice in urban forest plays an important role in both, storage capacity and free throughfall coefficient [9] . Horton’s framework theory [4] states that the maximum storage capacity can be reduced compared to air conditions when they are affected by the shake of branch and foliage caused by the wind during and after the rain event. Certainly, this idea produces a debate about the existence of single capacity storage without taking into account a possible duality of processes by hysteresis.
Generally in the literature, canopy’s storage capacity is expressed in mm; in this sense, Zinke [10] reported capacity storage values ranging from 0.25 to 9.14 mm per unit of vegetation area (Aston, 1979). This also applies for the throughfall coefficient. Yet, other constraints to parameterization of them are the devices and methodology of measurements. Interception measurements are estimated by placing long calibrated throughfall containers and rain-gauges underneath the canopy; these elements are distributed along the projected area. Lankreijer [11] measured percolation by using 8, 10 and 12 m long troughs of 0.10 m wide; rainwater from the troughs was collected in funnels. Rutter et al. [5] also used the same technique to study rainfall passing through the canopy. Domingo et al. [12] used funnels, while Schellenkens et al. (1999) used rain-gauges. Troughs and containers do not account for all the projected area and there is a bias in the measurements derived from them [13] . To integrate the total volume draining through the crown, a variety of these devices is needed to cover the total projected area and to determine throughfall and dripping. An associated problem with the use of these devices is the capturing of lateral rainfall because normally, rainfall presents an inclination angle [14] . This angle plays an important role in the operation of troughs and containers, and will potentially generate errors in the measurements. Kimmins [15] found that hundreds of containers are required to reduce error magnitude from 20% to 5%. Xiao et al. [16] developed a methodology to measure rainfall interception in urban areas. The methodology developed by Xiao [13] , is appropriate when rain comes down through the sides where the frames are located and when the maximum height of plastic sheets is enough to protect from the lateral rain entrance; however, if incident rain comes from a different direction, the frames are exposed to the lateral entrance of rain. With the methodology of Xiao et al. [16] , the measurement of net precipitation can be more accurate since the catchment totally covers the canopy tree; nevertheless, a detailed methodology is needed to improve the understanding of the dynamics of the canopy parameter as well as its storage capacity and throughfall. The coefficient of free throughfall (ρ) and canopy storage capacity (S) can be altered by the seasonal changes, development, or growth of the canopy structure [17] . In urban zones, these parameters are quickly affected due to pruning practices. To determine ρ and S, researchers have used techniques such as the minimum method and the linear regression between gross precipitation on x-axis and throughfall on y-axis [10] [18] - [20] . For example, Rutter et al. [21] and Klaassen et al. [19] found an S in P. menziesii of 1.2 and 2.4, respectively. In P. sylvestris, Gash and Morton [18] reported an S of 0.8 mm. The corresponding values for P. stichensis were 0.75 - 1.20 mm [6] . Link et al. [22] and Pypker et al. [17] observed in P. menzesii an S of 3.3 and 1.4, respectively. Therefore, a canopy’s parameter determination is needed to improve dynamic process of S on hydrological models. Canopy storage capacity varies, as rainfall intensity and meteorological factors affect the rainfall interception, and canopy structure grows seasonally. Hence, the objective of this study has evaluated the throughfall and storage capacity of an evergreen tree of isolated tree of urban zone. The particular aim of this research is to focus on individual rainfall events and to test the changes of ρ and S on the linear regression between gross precipitation and throughfall, leaving aside the problems associated with logging and pruning trees, and the Rutter and Gash models to predict interception losses were applied accordingly.
2. Materials and Methods
2.1. Site description
The study was conducted in the urban zone of Queretaro city, located at 20˚30' of latitude and 100˚23' longitude, 250 kilometers northwest from Mexico city, in an altitude of 1820 m above the sea level. The studied area covers 220 km2. The urban zone is located on the high central plateau of Mexico, between the Gulf of Mexico and the Pacific basin. This geographical location regulates the occurrence of convective-type precipitations. According to the National Water Commission (CONAGUA, initials in Spanish), mean annual rainfall in this city is 548 mm, with minimum and maximum values of 274 and 999.2 mm, respectively. Mean annual temperature is 18.7˚C, with a minimum of 17.4˚C and a maximum of 19.7˚C. Dominant wind direction is east and northeast with a mean speed of 1.7 m·s−1. Mean annual potential evaporation ranges from 2020 to 2200 mm. The vegetation in the urban zone of Queretaro does not have well defined spatial configuration, it is highly variable in types due to the lack of a sustainable planning of these activities, even though many efforts have been made to reforest the city with different types of vegetation. According to the Direction of Ecology and the Secretary for Public Municipal Services (Dirección de Ecología y Secretaría de Servicios Públicos Municipales) reforestation programs were implemented in the city during the 2000-2004 periods, where a total of 734,336 trees were planted around the city where sixty percent of the planted trees were non-native species. Many efforts have been made to reforest the city with different types of vegetation, trying to improve the regional climatic conditions. The urban non-native vegetation Ficus benjamina L. can be seen in Queretaro as one of the main types of trees.
2.2. Experimental field
The experimental study was carried out in a 15-year-old non-deciduous Ficus benjamina L. tree located in the main campus of the Universidad Autónoma de Querétaro (20˚35.44N, 100˚24.79W) at an elevation of 1819 m. In April 2005, the tree trunk was 1.10 m in height, with a 22.44 cm diameter; the crown diameter was 6.0 m with a total height of 5.70 m. In January 2006 the tree trunk was 1.10 m in height and 25.0 cm in diameter; the crown diameter was 6.18 m and its total height was 6.00 m. The tree was not pruned during the research. The selected tree is surrounded by several buildings at distances between 13 and 100 m. The nearest building is located at the east side of the tree and has a height of 2.80 m. Topography of the site is relatively flat and the surface was paved with asphalt.
2.3. Meteorological data collection
The meteorological station was located in an open area, approximately 100 m south-east from the study site. The temperature, wind speed and direction were recorded every 5 min. Gross precipitation was measured every 5 min by a tipping-bucket rain gauge (TE525LL-L; 0.254 mm per tip). Rainfall data collected in the study site were made during the years 2005 and 2006. In the year 2005, rainfall events occurred between July and October (rainy season), where 17 events were registered during the summer and 2 in autumn. In addition, 4 spring storms beginning in March were registered; other 15 events occurring in the summer (July) and 2 more in autumn (September) were measured in 2006. Most of the storms occurred during the afternoon, from 18:00 to 24:00 hours, with an average duration of 85 minutes.
2.4. Stemflow and throughfall measurements
For the stemflow collection, a spiral guide channel was wrapped around the tree bole. The channel was fabricated with a 2.54 cm diameter soft plastic garden hose. Gaps between the channels and the tree bole were stamped with silicone sealant. A water container of 20-L was used for storing stemflow. At the end of each storm, the stored water was measured using a1-L graduated cylinder having a 1/100 L precision. Throughfall was measured using a catchment under the canopy crown [1] . The catchment system was constructed in two different ways: in 2005, the catchment consisted of eight trapezoidal-shaped polyethylene sheets (2.1 m × 0.3 m × 2.7 m) to cover the total crown projection area, 25.90 m2. The sheets were supported with a steel frame, 1.60 m high on the outside and 0.50 m high on the inside, having a 0.10 m separation from the tree’s trunk. Each plastic sheet was 3.24 m2. The slope towards the inside of tree trunk was 36%. Throughfall collected in the plastic sheets drained to a 0.10 m wide circular PVC gutter with a 2% slope, connected to a 50-L container. Accumulated rainfall after each event was measured with a 1-L graduated cylinder having a 1/100 L precision. During 2006, the catchment from polyethylene sheet was changed to a rigid plastic sheet. The catchment was constructed from trapezoidal-shaped rigid sheets of 2.30 × 0.5 × 2.5 m plywood, covering a total canopy crown of 25.90 m2. A wooden base frame was used to support the rigid plastic sheet with a slope towards the tree bole of 45%. The change of the slope increased the velocity from throughfall to channels. Rigid plastic sheets terminated in four square-shaped sheet channels (0.10 × 0.10 m) with a slope of 2% and separated 0.10 m from the trunk. The sheet channels guided the water into a water throughfall container (200-L). Scale (capacity of 60 kg with an accuracy of 2 gr) was used to make the system work systematically, monitoring changes in the water level inside the container. The scale sent a signal to a register machine (data logger) sending the total weight to a computer. The computer saved the information each minute. The recording machine and the computer were located 30 m from the catchment (Figure 1). To avoid errors from lateral incident rain and residual throughfall produced by wind shaking the leaves during each event, a 0.50 m-tall protective polyethylene and rigid plastic screen was installed around the perimeter of the projected crown (in both catchment years; Figure 1).
3. Theory
The gross precipitation (Pg; incident rainfall on canopy) falling on the forest or isolated tree (urban trees) is intercepted by the tree’s canopy crown; then, a percentage of the Pg reaches the ground as net precipitation (Pn; net rainfall is the quantity that reaches the ground). As a result, the rainfall interception process works as a system. The system can be defined as the structure (Figure 2) that has inputs (rain) and outputs (net precipitation) linked together by a causing process [23] . According to the internal process of the system, the input and output are quite different. During a rainfall interception, the output can be both net precipitation and evaporation. Therefore, the total output is affected by storage inside the system. According to this system analogy, studies on rainfall interception have predicted the output behavior from a known input and internal processes. In this paper,
Figure 1. Scheme of the measurements systems for rainfall interception losses.
Figure 2. In the system, the input and output are the gross precipitation (Pg) and net precipitation (Pn) respectively. In the internal process there is water storage on surface canopy (S), evaporation (E), free throughfall (ρ), stemflow (St) and drainage (D).
such analogy is considered to show the behavior of the canopy storage due to the wind and canopy growth during the seasons. The system is linear if the input produces an equal output response. The input and output can be expressed as a function of time, I(t) and 0(t) respectability. Nonetheless, the system produces an input transformation on the output as:
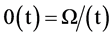 (1)
(1)
Equation (1) is known as the transformation equation of the system in which the symbol Ω, is the transfer function between the input and output. In the rainfall interception event, it represents the internal process of the system, in which the canopy water storage can be calculated as:
 (2)
(2)
From Equation (2) several methods have been developed to determine the rainfall interception.
3.1. Model of Rutter et al. (1971)
A physical interception model was developed by Rutter et al. [5] which regards the canopy as having capacity to store rain water on leaves and trunk surface (reservoir) that are emptied by evaporation at the end of the storm (Rutter et al., 1977). The volume of rain water retained on leaves and trunk surface depends on the position of the leaf surface, the leaf form, the surface tension relation between rain-drops and the leaf surface, as wind velocity, rainfall intensity and the size and impact of the falling drops [24] [25] . Equations (3) and (4) give the evolution of the rate canopy capacity of rainfall interception from Rutter’s model.
 (3)
(3)
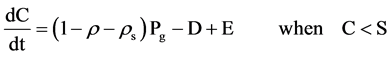 (4)
(4)
where: dC is the change in canopy storage; ρ is the free throughfall or precipitation that reaches the ground through the gaps between canopy leaves and branches without hitting the canopy surface; ρs is the stemflow and the flow water that reaches the ground by flowing down the tree bole. D corresponds to the rain drained by the vegetation canopy which is the water dripping from the surface of the leaves or branches after the storage capacity of the canopy is saturated (C = S). The S term corresponds to the storage capacity by interception of the reservoir. The rate (D) of drainage from the canopy is normally calculated as:
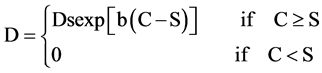 (5)
(5)
The value of b and Ds are empirical parameters of the vegetation and drainage rate at saturation respectability. The b and Ds were estimated by Rutter et al. [5] , in which b and Ds were 3.7 and 2 × 10−3 mm·min−1, respectively. These parameters are not easy to measure in natural conditions; however, Rutter’s parameter has been extrapolated for many researches in order to use Rutter’s model. Aboal et al. [26] extrapolated Rutter’s parameters and obtained b = 1.6 and Ds = 4.7 × 10−3 mm·min−1. On other hand, Valente et al. [7] describes the new version of the Rutter’s model in which empirical parameters are omitted of the drainage equation. Then, the drainage function was simplified as:
 (6)
(6)
Equation (6) means that any over-rain stored on the canopy is converted immediately into drainage and the drainage stops as soon as the rainfall ceases [7] .
Derivation of rainfall-interception canopy parameters
The two main parameters required for the interception models [5] [6] are thus ρ and S. These parameters represent the architecture of vegetation and characteristics of species of trees that controls interception loss. ρ cannot be directly determined, as a result, several methods have been developed such as, the slope of the regression between gross precipitation (Pg) and throughfall (Th). This method allows to obtain the free throughfall coefficient [5] [20] . The regression method is for storms that are too small to fill the canopy storage, in which evaporation loss during small storms are negligible (Shellekens et al., 1999).
To determine the storage capacity (S), direct and indirect methods have been developed. The first one consists of the wetting the vegetation surface, in which artificial rainfall is applied into a laboratory. The second method is commonly derived from the relationship between cumulative gross precipitation (Pg) and throughfall (Th). According to the indirect methodology, the canopy storage capacity is estimated by identifying the inflection point on the Th-axis (Equation (7)) in the Pg-Th relationship for storms which are intense enough to saturate the canopy [18] - [20] .
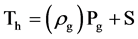 (7)
(7)
where: S is the thickness averaged over the total horizontal area of the tree. The storage capacity is also KP0, K corresponds to the tree mass covered area seen upwards from the ground, that is similar to the projected horizontal area supposed by Horton [4] . P0 is the precipitation which becomes the oversaturated canopy during and after the storm. Since it must be expected that the derivate of Th must be the unity [27] . Besides, this theory is only valid if the structure of the tree was permanent and inflexible.
3.2. Gash’s Model (1979)
The so-called analytical model of rainfall interception was proposed by Gash [6] . Gash’s model elegantly retains some of the simplifications and explicit reasoning in the Rutter’s model. The Gash model is based on regression equations that are coupled with the rigorous Rutter’s model. While Rutter’s model requires detailed meteorological data, Gash’s analytical model remains simple and is characterized by its low data demand. A simple linear relationship between the interception loss and gross rainfall is often used to describe rainfall interception [6] :
 (8)
(8)
where: I is the interception loss, Pg the rainfall, a and b are the regression coefficients. The coefficient b can estimate the canopy storage capacity (S); a represent the ratio of the mean evaporation rate from the wet canopy to the mean rainfall rate as given by equation
 (9)
(9)
Gash showed that 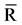 can be derived from all the storms under investigation, E should be obtained from the Penman equation. Assuming that neither
can be derived from all the storms under investigation, E should be obtained from the Penman equation. Assuming that neither  nor
nor 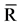 vary considerably, it is possible to calculate
vary considerably, it is possible to calculate 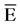 from a provided
from a provided 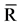 in the absence of above-canopy climatic observations (Schellekens et al., 1999) [28] . According to Gash´s model, regressions between gross precipitation (Pg) and throughfall (Th) show that Th increases linearly along with Pg until the canopy gets saturated. If the slope of Pg-Th relationship is less than 1, evaporation during rainfall is occurring but if it is greater than 1, precipitation interception exceeds evaporation. The analytical model of interception can be applied to given estimates of S, ρ and
in the absence of above-canopy climatic observations (Schellekens et al., 1999) [28] . According to Gash´s model, regressions between gross precipitation (Pg) and throughfall (Th) show that Th increases linearly along with Pg until the canopy gets saturated. If the slope of Pg-Th relationship is less than 1, evaporation during rainfall is occurring but if it is greater than 1, precipitation interception exceeds evaporation. The analytical model of interception can be applied to given estimates of S, ρ and 


where: 


4. Results
4.1. Rainfall and weather variability
From the 40 events recorded during 2005 and 2006, a total of 354.94 mm of rain was registered, of which 151.59 mm occurred on 2005 [1] and 203.35 mm occurred 2006, respectively (Table 1). During 2005, a total of 19 events took place between July to October, where 95% (144.29 mm) of the events occurred during the summer and 5% (7.30 mm) in autumn. The average rainfall intensity ranged from 1.20 to 20.31 mm·h−1, with a maximum rainfall intensity of 54.84 mm·h−1. The events registered in 2006 had an average rainfall rate from 0.65 to 25.97 mm·h−1, with a maximum rainfall intensity of 109.20 mm·h−1. From the 21 events registered in 2006, 28% (56.80 mm) occurred during the spring; 63% (127.95 mm) and 9% (18.60 mm) were measured in summer and through autumn, respectively. Rainfall storms occurred during the afternoon around 18:00 - 20:00 h in 2005, and around 17:00 - 24:00 h in 2006. The average time-lag varied from 8 h to 14 days during 2005 and 2 h to 29 days in 2006, so the time of no precipitation (threshold) was enough for the drying of the canopy. According to the registered data for the weather conditions, relative humidity at the beginning of each event was rather low, but it increased during the storm. The increase of humidity was due the high rate of temperature; therefore, evaporation was not limited to the event. Indeed, low relative humidity and high temperature allowed having a high rate of evaporation during the storm. The maximum wind gust during the events was 11.60 m·s−1 and 8.49 m·s−1 for 2005 and 2006, remaining close to zero during the events. Hence, the meteorological record suggested that temperature increases in response to storage heat of the urban zone, what is called urban heat island effect (Shephered, 2006). As a result, the gradient of urban microclimate can change more rapidly than in rural or natural forest, also affecting evaporation rate and temperature, modifying natural precipitation [29] [30] .
Table 1. Rainfall and weather characteristics for 2005 and 2006.
4.2. Rainfall partitioning
The measurements of both, the throughfall and stemflow for the two observation periods are summarized on Table 2. On the 2005 events, the net precipitation (Pn) was 61.45 mm, and it was measured as throughfall (57.82 mm) and stemflow (3.63 mm), where 92.6% of net precipitation occurred during summer. Otherwise, the net precipitation on 2006 was measured on three seasons, and it was 59.01 mm. Summer had more net precipitation (62% of Pn) during the 2006 events. The overall throughfall for summer was: 53.52 mm in 2005 and 36.06 mm in 2006. The stemflow depth in 2005 (3.38 mm) was slightly more than in 2006 (2.52 mm) during summer. During autumn, total measurements of throughfall varied from 4.30 mm to 1.67 mm in 2005 and 2006, respectively. We believe that the intensity of precipitation, wind speed and relative humidity were factors that can explain the differences in the partition of precipitation.
4.3. Rainfall interception
Rainfall interception was determined as the difference between gross precipitation (Pg) and net precipitation (Pn is the sum of throughfall and stemflow). The total interception of each period was 90.14 mm (59.5% of Pg) and 144.34 mm (71% of Pg); with an average rainfall intensity of 20.32 mm·h−1 and 25.97 mm·h−1. The rainfall interception by the Ficus benjamina L. tree was relatively high due to the high temperature and low relative humidity at the beginning of each event. In the same way, the interception of rain may not be constant for the weather variables as well as the phenology of the tree. It is well known that anthropogenic activities modify or alter the natural environment, creating an urban environment where the microclimate gradient can vary quickly representing a key role in the rainfall interception process; so, interception loss derived from the forest cannot be extrapolated to urban forests [30] .
4.4. Storage capacity and free Throughfall coefficient
Surface storage capacity (S) and free throughfall coefficient (ρ) were estimated based on the relationship between gross precipitation (Pg) and throughfall (Th) data [5] [18] . The relationship based on Pg and Th from 2005 events determinate that S equals to 1.53 mm [1] . But the surface capacity cannot be assumed to be constant through time because S can be affected by moisture, temperature and evaporation rate as well as by the seasonally phenological development of vegetation and pruning practices [22] . However, wind speed and shaking cause leaves and branches dripping during and before storage capacity is reached, as well as when the precipitation ends (Xiao et al., 2000) altering the rainfall interception between events and season periods; in the same
Table 2. Summary of precipitation (Pg), throughfall (Th), stemflow (St), net precipitation (Pn) and interception (I).
way, ρ is affected. The advantage of using the catchment system during 2006 was to measure the dynamic of Th during each storm. Then, the dynamics of S and ρ by events were calculated by plotting Pg versus Th, in which a linear regression analysis was used for each rainfall event. Table 3 summarizes the dynamics of S and ρ during the events of 2006.
Two different criteria were used for selecting data to calculate ρ and S in order to guarantee the completeness of the canopy saturation: 1) for all gross precipitation with rainfall less of 10.00 mm, ρ was calculated; 2) for all events with rainfall over 10.00 mm, S was determined. The average values for S and ρ were 1.36 mm and 0.31, respectively. Storage capacity ranged from 1.00 mm to 2.03 mm and free throughfall coefficient from 0.10 to 0.64. Remarkably the maximum storage capacity value for Ficus benjamina L. was similar to the reported by Xiao et al. [25] for Pyrus calleryana (pear tree; S = 1.00 mm) and Quercus suber (Oak tree; S = 2.00 mm), and the maximum free throughfall coefficient also was similar to the pear tree (ρ = 0.6) but higher than that for the oak tree (ρ = 0.3). Due to the high density of crown and different tree architecture between forest and urban forest, the parameters obtained for forest may not be comparable and applicable to urban trees. The determination of canopy parameters (S and ρ) at the urban environment associated with seasonal canopy variation is needed to improve the understanding of canopy storage variation. Briefly, average storage capacity during the spring (S = 1.35) was fairly similar to the one during the summer (S = 1.32) therefore, no relationship was found between S and ρ. The variation range in ρ also may result from variation in raindrop sizes (Calder, 1996) and dislodging of intercepted drop by wind gust as well as developmental changes in crown structure and environmental conditions during periods of rainfall [17] [22] . Moreover, urban vegetation is always under stress due to urban environment variation which affects the foliage. During the spring and summer periods, rainfall intercepted by the Ficus benjamina L. tree showed that the wind speed plays an important role in the amount of water retained by the canopy. In the case of events of May 30th, 2006 and August 16th 2006 the interception was 1.95 mm and 1.64 mm, with 2.20 mm of precipitation in each storm. However, the difference of rainfall intercepted was due the wind gust and temperature during of the storm. At the event on May 30th, 2006, the wind speed was 1.93 m·s−1 with an initial temperature of 14.53˚C. At the event on August 16th, 2006, the wind speed decreased (1.02 m·s−1) and the temperature increased (15.45˚C) consequently, being slightly less than the one of May 30th (1.64 mm). Moreover, But compared coparison of the results with ρ parameter indicated that the biomass of Ficus benjamina L. decreased from spring to summer, affecting Th and St as well as S.
Figure 3 and Figure 4 show detailed rainfall and meteorological parameters measured at 10-min and 5-min intervals as well as the evolution of cumulative gross precipitation, and throughfall for events of May 18th, 2006 (Figure 3) and August 15th, 2006 (Figure 4). The first event took place during spring with a duration of 180 min (3 h). During this storm the gross precipitation was of 24.10 mm. The maximum temperature (12.88˚C) and low humidity (69.17%) occurred at the beginning of the event. The second event occurred during summer season which lasted 55 min (0.83 h) and had 12.30 mm of precipitation. During this event, the maximum temperature was 16.42˚C at the beginning of the rainfall event. The maximum humidity was 84.11% min after the storm started. In both events high temperature and low relative humidity were associated, in which interception loss was relatively high: 15.46 mm (64%) for event of May 18th and 11.38 mm (92%) for August 15th. According with the meteorological condition, the high interception loss can be attributed to the wind gust inducing greater evaporation by convection. For the event of May 18th the canopy tree and raindrops hitting the leaves and branches caused crown drip to occur in less than 10 min, before the saturation capacity was reached. After 15 min of rain, wind gust (4.25 m·s−1) produce enough shaking to cause great movement of the canopy tree, causing dripping and increasing the troughfall. By the time high wind speed ceased, the empty canopy and high rate of
Table 3. Changes of interception, storage capacity, gap fraction and discharge in 2006.
evaporation tended to speed up the rainfall interception. But in the last period of the event, the rainfall interception decreased due to the wind gust of 0.5 m·s−1 speed. Therefore, available water for interception did not only depend on the intensity of the rainfall, but also on the wind speed. Such characteristics would tend to modify storage capacity. Figure 4 shows a rainfall event that lasted less than 60 min (August 15th). Interception and throughfall did not differ as they did in the event of May 18th. Yet, the dynamics of rainfall interception were parallel to gross precipitation and throughfall was close to zero. When the rain stopped during a brief period (5 min), interception was negative because the wind blowing on the canopy caused dripping. Furthermore, the high interception of rain was due to the high evaporation rate, it can be evident by the increase of relative humidity during the event. Also high wind speed increased evaporation from the wet tree surface [25] , but increased the rate of dripping, while ρ could be quickly modified during the dynamic of rainfall interception. Such characteristics, as well as the nature of the vegetation and the weather, would also tend to modify the storage capacity of each event. Finally, despite of the wind speed being able to modify rainfall interception during each event, interception was greater than throughfall.
5. Discussion
5.1. Simulated data from Rutter’s model
The values of the free throughfall coefficient (ρ) and storage capacity (S) parameters were estimated according to the procedures described above. To get an estimate of the canopy parameters b and Ds, the values obtained by Rutter et al. [5] were extrapolated to the Ficus benjamina b is taken to be 3.7 × S/1.05 and Ds to be 0.002 × S/1.05. As a result, the b value was 6.29, and the Ds value was 3.4 × 10−3 mm·h−1. The required meteorological
Figure 3. Dynamic process of event of May 18th, 2006: (a) Accumulated gross precipitation (Pg), Interception (I), Throughfall (Th); (b) Distribution of precipitation, interception, throughfall, wind speed; and (c) Meteorological data.
parameters are the average rainfall intensity (






Figure 4. Dynamic process of event of August 15th, 2006: (a) Accumulated gross precipita- tion (Pg), Interception (I), Throughfall (Th); (b) Distribution of precipitation, interception, throughfall, wind speed; and (c) Meteorological data.
5.2. Simulated data from Gash’s model
The amount of rainfall needed to completely saturate the canopy was determined with Equation (10). The 





Table 4. Partitioning of interception losses among the different modeled stages of rainfall events in the Rutter and Gash models.
buted to the Gash model overestimating interception. In the Rutter’s model, under-estimation of interception losses was estimated assuming 
Figure 5. Regressions of measured interception losses against interception losses predicted by: (a) the model of Rutter (∆) and (b) the model of Gash (O).
terception during rainfall events, respectively. The Rutter’s model markedly underestimates interception loss during events with more than 20 mm of gross precipitation, this means that the model depends on the amount of rainfall around of tree. In contrast, the Gash’s model presented a slightly better fit when predicting interception loss against gross precipitation. Then, Figure 6 shows that the best prediction was obtained with the Gash’s model, whether using the linear regression of interception versus the gross precipitation method for estimating

6. Conclusion
The amount of water stored on the crown surface by interception of vegetation and the effect on surface runoff in large urban areas still require further research considering the fact that the trees are supple. The two main urban variables involved in this research: the meteorological condition and the vegetation parameters, present a different behavior from that in forest conditions. The detailed rainfall, throughfall and meteorological data measurement showed that S and ρ changed between events and seasonally in the Ficus benjamina L. tree. The storage capacity of the Ficus bejamina L. tree cannot be considered constant, because the structure of this tree is not steady. The structure of the tree changes from one season to another. The most foliage mass occurs during spring and summer; hence, the storage capacity is higher in these seasons. The free throughfall is also determined by structural changes in the tree. During winter, the free throughfall should be higher than that during summer. It could be considered that the storage capacity is proportional to the growth of the leaf mass while the free throughfall is inversely proportional. Trees in natural conditions are not under the same condition as trees located in urban zones. The trees located in cities are under regular stress, as a result of urban heat island effect, vehicles, people, etc. Hence, the urban trees loss foliages mass more quickly than a tree on a natural environment or even it does not reach its full development. As a result, significant changes on storage capacity and free throughfall occur. The free throughfall is proportional to wind speed; during a significant wind speed, raindrops retained on the surface of leaves and branches fall to the ground. Therefore, free througfall increases as a result of wind. The determination of canopy parameters associated with urban environment is needed to improve the understanding of the role of the vegetation in runoff control and managing urban forest for hydrologic benefits. The interception loss is the result of the storage capacity and free throughfall. If the storage capacity changes the
Figure 6. Regressions of gross precipitation against interception losses predicted by: (a) the model of Rutter (∆) and (b) the model of Gash (O).
interception loss also changes. The models developed for determining interception losses do not consider the conditions of the urban trees; therefore, modeled interception is unlikely to be similar to the estimated. The marked differences between measured interception and predictable interception are attributed to extremely high temperatures and change of the urban climatic characteristics. These conditions may be partially attributed to the reduced or increased sensitivity of the models. Yet, the slightly best prediction of the interception losses was obtained with the Gash’s model.
Acknowledgements
This work was financially supported by the Consejo Nacional de Ciencia y Tecnologia (CONACYT). The authors wish to express their gratitude to the Head of the School of Engineering Division for Graduate Studies at the Universidad Autónoma de Querétaro and to the Master Degree Program of Water Resources and Environmental Engineering.
References
- Guevara, E.A., González, S.E., Véliz, Ch.C., Ventura, R.E. and Ramos, S.M. (2006) Rainfall Interception and Distribution Patterns of Gross Precipitation Around and Isolated Ficus benjamina Tree in an Urban Area. Journal of Hydrology, 333, 532-241. http://www.sciencedirect.com/science/article/pii/S0022169406005038 http://dx.doi.org/10.1016/j.jhydrol.2006.09.017
- Xiao, Q. and Mcpherson, E. (2003) Rainfall Interception by Santa Monica’s Municipal Urban Forest. Urban Ecosystems, 6, 291-302. http://link.springer.com/article/10.1023/B:UECO.0000004828.05143.67 http://dx.doi.org/10.1023/B:UECO.0000004828.05143.67
- Crockford, R.H. and Richardson, D.P. (1990) Partitioning of Rainfall in a Eucalypt Forest and Pine Plantation in Southeastern Australia: IV. The Relationship of Interception and Canopy Storage Capacity, the Interception of These Forest, and the Effect on Interception of Thinning the Pine Plantation. Hydrological Processes, 4, 169-188. http://onlinelibrary.wiley.com/doi/10.1002/hyp.3360040207/pdf http://dx.doi.org/10.1002/hyp.3360040207
- Horton, E.R. (1919) Rainfall Interception. Monthly Weather Review, 47, 603-623. http://dx.doi.org/10.1175/1520-0493(1919)47<603:RI>2.0.CO;2
- Rutter, J., Kershaw, K., Robins, P. and Morton, A.J. (1971) A Predictive Model of Rainfall Interception in Forest, 1. Derivation of the Model from Observations in a Plantation of Corsican Pine. Agricultural Meteorology, 9, 367-384. http://www.sciencedirect.com/science/article/pii/0002157171900343
- Gash, J.H.C. (1979) An Analytical Model of Rainfall Interception by Forests. Quarterly Journal of the Royal Meteorological Society, 105, 43-45. http://onlinelibrary.wiley.com/doi/10.1002/qj.49710544304/pdf http://dx.doi.org/10.1002/qj.49710544304
- Valente, F., David, J.S. and Gash, J.H.C. (1997) Modelling Interception Loss for Two Sparse Eucalypt and Pine Forest in Central Portugal Using Reformulated Rutter and Gash Analytical Model. Journal of Hydrology, 190, 141-162. http://www.sciencedirect.com/science/article/pii/S0022169496030661 http://dx.doi.org/10.1016/S0022-1694(96)03066-1
- Jones, J.R. (1976) Physical Data for Catchment Models. Nordic Hydrology, 7, 245-264. http://www.iwaponline.com/nh/007/nh0070245.htm
- Asdak, C. (2003) Evaporated of Interception Precipitation in Unlogged and Logged Forest Areas of Central Kalimatan, Indonesia. Water Resources System-Water Availability and Global Change (Proceedings of Symposium). IASH No. 208, 275-281.
- Zinke, P.J. (1967) The Patterns of Influence of Individual Forest Tree on Soil Properties. Ecology, 43, 130-133. http://www.jstor.org/stable/1932049 http://dx.doi.org/10.2307/1932049
- Lankreijer, H., Hendriks, J. and Klaassen, W. (1993) A Comparison of Models Simulating Rainfall Interception of Fo- rest. Agricultural and Forest Meteorology, 64, 187-199. http://dx.doi.org/10.1016/0168-1923(93)90028-G http://www.sciencedirect.com/science/article/pii/016819239390028G
- Domingo, F., Sánchez, G., Moro, M., Brenner, A. and Puigdefabregas, J. (1998) Measurement and Modelling of Rainfall Interception by Three Semi-Arid Canopies. Agricultural and Forest Meteorology, 91, 275-292. http://www.sciencedirect.com/science/article/pii/S0168192398000689 http://dx.doi.org/10.1016/S0168-1923(98)00068-9
- Xiao, Q. (1999) Rainfall Interception of Urban Forest. Ph.D. Dissertation, University of California, Davis, 184 p.
- Bruijnzeel, L.A. (2001) Hydrology of Tropical Montane Cloud Forest: A Reassessment. Land Use and Water Resources Research, 1, 1.1-1.18.
- Kimmins, J.P. (1973) Some Statistical Aspects of Sampling Throughfall Precipitation in Nutrient Cycling Studies in British Columbian Coastal Forests. Ecology, 54, 1008-1019. http://ican.csme.utah.edu/wp-content/uploads/2012/02/Kimmins-1973.pdf
- Xiao, Q., McPherson, E.G., Ustin, S.L. and Grismer, M.E. (2000) A New Approach to Modeling Tree Rainfall Interception. Journal of Geophysical Research, 29, 173-188.
- Pypker, T.G., Bond, B.J., Link, T.E., Marks, D. and Unsworth, M.H. (2005) The Importance of Canopy Structure in Controlling the Interception Loss of Rainfall: Examples from Young and an Old-Growth Douglas-Fir Forest. Agricultural and Forest Meteorology, 130, 113-129. http://www.sciencedirect.com/science/article/pii/S016819230500064X
- Gash, J.H.L. and Morton, A.J. (1978) An Application or the Rutter Model to the Estimation of the Interception Loss from Thetford Forest. Journal of Hydrology, 38, 49-58. http://www.sciencedirect.com/science/article/pii/0022169478901312 http://dx.doi.org/10.1016/0022-1694(78)90131-2
- Klaassen, W., Bosveld, F. and De Water, E. (1998) Water Storage and Evaporation as Constituents of Rainfall Intercep- tion. Journal of Hydrology, 212-213, 36-50. http://www.sciencedirect.com/science/article/pii/S0022169498002005 http://dx.doi.org/10.1016/S0022-1694(98)00200-5
- Leyton, L., Reynolds, E.R.C. and Thompson, F.B. (1967) Rainfall Interception in Forest and Moorland. In: Sopper, W.E. and Lull, H.W., Eds., Forest Hydrology, Pergamon, Oxford, 163-178.
- Rutter, J. and Morton, A.J. (1977) A Predictive Model of Rainfall Interception in Forest. Sensitivity of the Model to Stand and Parameters and Meteorological Variables. Journal of Applied Ecology, 14, 567-588. http://www.jstor.org/stable/2402568 http://dx.doi.org/10.2307/2402568
- Link, T.E., Unsworth, M. and Marks, D. (2004) The Dynamics of Rainfall Interception by a Seasonal Temperate Rain- forest. Agricultural and Forest Meteorology, 124, 171-191. http://dx.doi.org/10.1016/j.agrformet.2004.01.010 http://www.sciencedirect.com/science/article/pii/S0168192304000176
- Keim, R.F. and Skaugset, A.E. (2004) A Linear System Model of Dynamic Throughfall Rates Beneath Forest Canopies. Water Resources Research, 40, Published Online. http://onlinelibrary.wiley.com/doi/10.1029/2003WR002875/full http://dx.doi.org/10.1029/2003WR002875
- Schellekens, J., Scatena, F., Bruijnzeel, L. and Wickel, A. (1999) Modelling Rainfall Interception by a Lowland Tropical Rain in Forest in Northeastern Puerto Rico. Journal of Hydrology, 225, 168-184. http://www.sciencedirect.com/science/article/pii/S0022169499001572 http://dx.doi.org/10.1016/S0022-1694(99)00157-2
- Xiao, Q., McPherson, E.G., Ustin, S.L., Grismer, M.E. and Simpson, J.R. (2000) Winter Rainfall Interception by Two Mature Open-Grown Tree in Davis, California. Hydrological Processes, 14, 763-784. http://www.itreetools.org/streets/resources/Winter_rainfall_interception_Xiao.pdf
- Aboal, J.R., Jiménez, M.S., Morales, D. and Hernandez, J.M. (1999) Rainfall Interception in Laurel Forest in the Canary Islands. Agricultural and Forest Meteorologyis, 97, 73-86. http://www.sciencedirect.com/science/article/pii/S0168192399000830 http://dx.doi.org/10.1016/S0168-1923(99)00083-0
- Bringfelt, B. and Harsmar, P. (1974) Rainfall Interception in a Forest in the Eleven Hydrological Representative Basin. Hydrology Research, 5, 146-165. http://www.iwaponline.com/nh/005/nh0050146.htm
- Dykes, A.P. (1997) Rainfall Interception from a Lowland Tropical Rainforest in Brunei. Journal of Hydrology, 200, 260-279. http://www.sciencedirect.com/science/article/pii/S0022169497000231 http://dx.doi.org/10.1016/S0022-1694(97)00023-1
- Shepherd, J.M. (2006) Evidence of Urban-Induced Precipitation Variability in Arid Climate Regimes. Journal of Arid Environments, 67, 607-628. http://www.sciencedirect.com/science/article/pii/S0140196306000942 http://dx.doi.org/10.1016/j.jaridenv.2006.03.022
- Xiao, Q., McPherson, E.G., Simpson, J.R. and Ustin, S.L. (1998) Rainfall Interception by Sacramento’s Urban Forest. Journal of Arboriculture, 24, 235-244. http://www.itreetools.org/streets/resources/rainfall_interception_by_sacramentos_uf_xiao.pdf
NOTES
*Corresponding author.









