Journal of High Energy Physics, Gravitation and Cosmology
Vol.03 No.02(2017), Article ID:75704,8 pages
10.4236/jhepgc.2017.32030
Gedanken Experiment for Initial Expansion of the Universe and Effects of a Nearly Zero Inflaton in Pre-Planckian Physics Space-Time Satisfying Traditional Slow Roll Formulas Which Happens in Pre-Planckian Regimes Even If 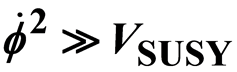
Andrew Walcott Beckwith
Physics Department, College of Physics, Chongqing University Huxi Campus, Chongqing, China

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 1, 2017; Accepted: April 24, 2017; Published: April 27, 2017
ABSTRACT
We first of all consider what if the initial inflaton was nearly zero instead of proportional to a Planck mass, in a SUSY type potential. Using the construction of Padmanabhan about general inflaton physics and the conditions of what are usual constituent slow roll requirements for inflation, and also of Kolb, Pi and Raby about a SUSY potential, we come up with the counter intuitive formulation of how usual tests for slow roll give the standard answers even if the inflaton in the SUSY potential as given by Kolb, Pi, and Raby is initially zero. The result gives support to a formulation of VEV conditions used right after a Planck instant of time. As it is, we will from first principles examine what adding acceleration does as to the HUP previously derived. In doing so we will be tying it in our discussion with the earlier work done on the HUP. The HUP results, so modified are appropriate for the Pre-Planckian results and may explain why the slow roll formulation as given by Padmanabhan holds where there is the phenomenon of 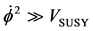 for Pre-Planckian space-time. This leads to a very paradoxical result that in Pre-Planckian physics the traditional slow roll formulas are satisfied even if
for Pre-Planckian space-time. This leads to a very paradoxical result that in Pre-Planckian physics the traditional slow roll formulas are satisfied even if . But it also puts in extremely tight restrictions upon the formulation of the degree of freedom problem, as given in Equation (26) in this document.
. But it also puts in extremely tight restrictions upon the formulation of the degree of freedom problem, as given in Equation (26) in this document.
Keywords:
Inflaton, SUSY, VEV, Heisenberg Uncertainty Principle, Slow Roll, Pre-Planckian

1. Introduction to the Basic Problem, as Far as SUSY Potential Physics. Starting off with a Summary of Why 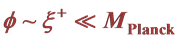 in
in  Situations, so the Square of H, Is >0
Situations, so the Square of H, Is >0
In this introduction, we use the results of how we set the state for a modified Pre-Planckian physics HUP. This will be leading to initial conditions which will lead to, later 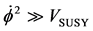 in Pre-Planckian space-time physics, which will in turn lead to our main analysis result that in the Pre-Planckian Space-time, that
in Pre-Planckian space-time physics, which will in turn lead to our main analysis result that in the Pre-Planckian Space-time, that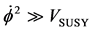 , will still lead to space-time conditions for which we have, the slow roll conditions, as outlined by Padmanabhan [1] , which merge seamlessly into the inflationary conditions, even if, in the Planckian space-time we have
, will still lead to space-time conditions for which we have, the slow roll conditions, as outlined by Padmanabhan [1] , which merge seamlessly into the inflationary conditions, even if, in the Planckian space-time we have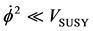 . In the regime which we have
. In the regime which we have  we have that
we have that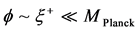 , for times t
, for times t  Planck time interval. By the time we have
Planck time interval. By the time we have  we have that
we have that 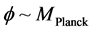 for Planck time. One of the findings will be that the square of the Hubble parameter, when
for Planck time. One of the findings will be that the square of the Hubble parameter, when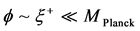 , will be > 0 only if
, will be > 0 only if , which occurs when the time is in the Pre-Planckian space-time regime and
, which occurs when the time is in the Pre-Planckian space-time regime and  when time is Planck time in value, just before the advent of inflation. In doing so, if
when time is Planck time in value, just before the advent of inflation. In doing so, if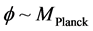 ,
,  no longer holds. But to get to this derivation, we will attempt to set up a modification of the HUP which will be part of how
no longer holds. But to get to this derivation, we will attempt to set up a modification of the HUP which will be part of how 



2. Re-Hash of Discussion Given in [2] about Modification of HUP
As stated in [2] we will be examining a Friedmann equation for the evolution of the scale factor, using explicitly one case being when the acceleration of expansion of the scale factor is kept in, and the intermediate cases of when the acceleration factor, and the scale factor is important but not dominant. In doing so we will be tying it in our discussion with the earlier work done on the HUP but from the context of how the acceleration term will affect the HUP, and making sense of [2]

Namely we will be working with [2]

i.e. the fluctuation 


In short, we would require an enormous “inflaton” style 



Here, [2]

3. What Is the Argument against the Usual Heisenberg Uncertainty Principle?
We will be looking at the likelihood of recovery of the usual Heisenberg uncertainty principle as would be seen if [2]

In short, we would require an enormous “inflaton” style 



4. The SUSY Potential Utilized. And Its Role for 

Going to Kolb, Pi, and Raby, [5] we outline certain problems with the usual SUSY models which in effect argues strongly against a scalar value 


With [ ] a minimum value for Equation (23) according to the first derivative, 


Were this followed, we would also would have a defined mass, for the scalar field which is given in [ ] by the following

With a minimization of a SUSY style Equation (7), and Equation (9) below if


i.e. this is still, with some tweaking a commonly accepted SUSY VeV model, with a minimum if

So, 
5. Examining What Happens to Equation (10) If in Pre Planckian Space Time 
We will be looking at the value of Equation (10) if

If we use the following, from the Roberson-Walker metric [2] [6] [7] .

Following Unruth [8] [9] , write then, an uncertainty of metric tensor as, with the following inputs

Then, the surviving version of Equation (7) and Equation (8) is, then, if 

This Equation (14) is such that we can extract, up to a point the HUP principle for uncertainty in time and energy, with one very large caveat added, namely if we use the fluid approximation of space-time [10]

Then [2]

Then,

How likely is
6. How We Can Justifying Writing 
To begin this process, we will break it down into the following co ordinates. In the rr, 



If as an example, we have negative pressure, with







1) Working with Equation (10) as a link to 
The key equation is to look at the following expression for the Hubble parameter, which is [1]

Here, we will be having 


2) Working with Slow Roll If we are using Equation (20) if
From using Padmanabhan [1] , we have the following which we write as for slow roll parameters

Then, if

Note that this is commensurate with this K.E. as proportional to have the left side of Equation (22) almost infinite in value and in turn that also relates to

Which due to [11] becomes similar to using Equation (24) in

Then by Equation (23) and Equation (24)

If we are in a very small Pre-Planckian regime of space-time, we could, then write Equation (24) as then proportional to 



As given by Kolb and Turner, the projected degrees of freedom max out about 110, while unorthodox treatment of the same problem lead to an upper bound of about 1000. Needless to say though, the given Equation (26) only works if there is an extremely small, almost zero inflaton value, as given by the following:
7. Conclusion
We think the only explanation is that even if Equation (21) and Equation (22) are not satisfied with an almost zero inflaton magnitude, the only explanation we have is of a causal discontinuity which would effectively wipe out a good deal of the information and structure from Pre-Plankian to Planckian space time, even if the behavior of Equation (21) and Equation (22) is commensurate with the Planckian slow roll conditions. We will write more of this in a subsequent publication. This will complete our full development of an extension of [12] as well as issues raised in [13] , and [14] where Corda calculated the magnitude of the inflaton, which has results which we will try to reconcile as to our present theoretical developments.
Acknowledgements
This work is supported in part by National Nature Science Foundation of China Grant No. 11375279.
Cite this paper
Beckwith, A.W. (2017) Gedanken Experiment for Initial Expansion of the Universe and Effects of a Nearly Zero Inflaton in Pre-Planckian Physics Space-Time Satisfying Traditional Slow Roll Formulas Which Happens in Pre-Planckian Regimes Even If
References
- 1. Padmanabhan, T. (2005) Understanding Our Universe, Current Status and Open Issues. In: Ashatekar, A., Ed., 100 Years of Relativity, Space-Time Structure: Einstein and Beyond, World Scientific Publishing, Singapore, 175-204. http://arxiv.org/abs/gr-qc/0503107
- 2. Beckwith, A. (2016) Gedanken Experiment for Refining the Unruh Metric Tensor Uncertainty Principle via Schwarzschild Geometry and Planckian Space-Time with Initial Nonzero Entropy and Applying the Riemannian-Penrose Inequality and Initial Kinetic Energy for a Lower Bound to Graviton Mass (Massive Gravity). Journal of High Energy Physics, Gravitation and Cosmology, 2, 106-124.
- 3. Barbour, J. (2009) The Nature of Time. http://arxiv.org/pdf/0903.3489.pdf
- 4. Barbour, J. (2010) Shape Dynamics: An Introduction. In: Finster, F., Muller, O., Nardmann, M., Tolksdorf, J. and Zeidler, E., Eds., Quantum Field Theory and Gravity, Conceptual and Mathematical Advances in the Search for a Unified Framework, Birkhauser, Springer-Verlag, London, 257-297.
- 5. Kolb, E., Pi, S. and Raby, S. (1984) Phase Transitions in Super Symmetric Grand Unified Models. In: Fang, L. and Ruffini, R., Eds., Cosmology in the Early Universe, World Press Scientific, Singapore, 45-70.
- 6. Gorbunov, D. and Rubakov, V. (2011) Introduction to the Theory of the Early Universe, Cosmological Perturbations and Inflationary Theory. World Scientific Publishing, Singapore.
- 7. Gutfreund, H. and Renn, J. (2015) The Road to Relativity, the History and Meaning of Einstein’s “The Foundation of General Relativity” (Featuring the Original Manuscript of Einstein’s Masterpiece). Princeton University Press, Princeton and Oxford, Princeton, New Jersey.
- 8. Unruh, W.G. (1986) Why Study Quantum Theory? Canadian Journal of Physics, 64, 128-130. https://doi.org/10.1139/p86-019
- 9. Unruh, W.G. (1986) Erratum: Why Study Quantum Gravity? Canadian Journal of Physics, 64, 145.
- 10. Giovannini, M. (2008) A Primer on the Physics of the Cosmic Microwave Background. World Press Scientific, Hackensack, New Jersey. https://doi.org/10.1142/6730
- 11. Kolb, E.W. and Turner, M.S. (1990) The Early Universe. Addison-Wesley Publishing Company, The Advanced Book Program, Redwood City, California.
- 12. Handley, W.J., Brechet, S.D., Lasenby, A.N. and Hobson, M.P. (2014) Kinetic Initial Conditions for Inflation. http://arxiv.org/pdf/1401.2253v2.pdf
- 13. Fredenhagen, K. and Rejzner, K. (2010) Local Covariance and Background Independence. In: Finster, F., Muller, O., Nardmann, M., Tolksdorf, J. and Zeidler, E., Eds., Quantum Field Theory and Gravity, Conceptual and Mathematical Advances in the Search for a Unified Framework, Birkhauser, Springer-Verlag, London, 15-23.
- 14. Corda, C. (2011) Primordial Gravity’s Breath. http://arxiv.org/abs/1110.1772





