Journal of Applied Mathematics and Physics
Vol.06 No.11(2018), Article ID:88845,20 pages
10.4236/jamp.2018.611204
The Power of Group Generators and Relations: An Examination of the Concept and Its Applications
Tiancheng Zhou
Shanghai Pinghe School, Shanghai, China

Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 20, 2018; Accepted: November 26, 2018; Published: November 29, 2018
ABSTRACT
This paper investigates the approach of presenting groups by generators and relations from an original angle. It starts by interpreting this familiar concept with the novel notion of “formal words” created by juxtaposing letters in a set. Taking that as basis, several fundamental results related to free groups, such as Dyck’s Theorem, are proven. Then, the paper highlights three creative applications of the concept in classifying finite groups of a fixed order, representing all dihedral groups geometrically, and analyzing knots topologically. All three applications are of considerable significance in their respective topic areas and serve to illustrate the advantages and certain limitations of the approach flexibly and comprehensively.
Keywords:
Generators and Relations, Free Group, Dyck’s Theorem, Dihedral Group Presentation, Classification of Finite Groups (Application), Realizing Dihedral Groups Geometrically (Application), Knot Group (Application)

1. Introduction
Ever since its establishment, the concept of groups has been central to the subject of abstract algebra. Groups are most commonly described by Cayley tables and Cayley graphs, both displaying all of their elements and most of the results of the group operation. After studying those two methods and a number of other related topics in group theory in detail at Stanford University Mathematics Camp (SUMaC) in summer 2017, my understanding invited me to think about groups in other ways and enabled me to explore related theories and applications independently. This paper sums up most of my original work on the third way of presenting groups: using generators and relations.
The main reason why I chose to delve into this topic is that generators and relations turned out to be a quintessential tool in capturing group structures. They proved able to fit flexibly into various situations and reveal insightful properties of groups that are hardly conceivable otherwise. Deeply fascinated by such adaptability and simplifying power, I aimed to show a bigger picture than merely their formal definitions and basic theorems through a wide array of their applications, from the presentations of dihedral groups and the quaternion group to the algebraic classification of finite groups, geometric representation of dihedral groups, and construction of knot groups.
One of the earliest presentations of a group by generators and relations was given by the Irish mathematician William Rowan Hamilton in 1856, in his icosian calculus―a presentation of the icosahedral group [1] . Starting from there, the first systematic study was given by Walther von Dyck (who later gave name to the prestigious Dyck’s Theorem), student of Felix Klein, in the early 1880s [2] . In his paper, Dyck defined (without giving it a name) the free group generated by a finite number of generators and described an interpretation of a group with a given presentation, where each generator is represented by a product of two inversions with respect to tangent circles or secants. His study laid the foundation for combinatorial group theory, but it was not until 1924 when a topologist Jakob Nielsen introduced the terminology free group in the first deep study of its properties [3] .
Since then, the topic of group presentation and free group has been widely studied by mathematicians: Standard notions and methods are systematically described in many teaching materials and notes in abstract algebra, such as Joseph Gallian’s comprehensive introductory book Contemporary Abstract Algebra [4] and Florian Bouyer’s notes titled Presentation of Groups [5] , which starts from the preliminaries of group presentation and free groups and investigates topics such as coset enumeration, presentation of subgroups, Baumslaq-Solitar Groups, and the Burnside problem.
As of pure research, most current and recent works are focused on determining the presentation of advanced-level group structures or interpreting complex group presentations. For example, Birman et al. [6] studied how generators and relations could be used in the presentation of the n-strong braid group. Karim Belabas and Herbert Gangl [7] investigated the methods to compute the group presentation of K2OF, the Milnor K-group of the ring of integers OF in a number field
The fact that there exists little work resembling this study illustrates its uniqueness in angle as well as findings: This paper examines the applications of group presentation from its very basics so that the notion is accessible for elementary math-learners. By incorporating creative devices such as “formal words” defined from a set, free groups defined with homophones, as well as generators defined in terms of mirror reflections, it offers vivid constructive examples while linking the ideas to higher-level areas―All three applications discussed in this paper can be examined in greater depths. Based on the findings of this paper, one is encouraged to further explore the classification of higher-order finite groups, geometric presentation of quaternion groups and dihedral and quaternion groups in higher dimensions, as well as methods to compute the group presentation for complicated knots or to construct knots from their groups written in terms of generators and relations. In this sense, this paper serves as a valuable reference and source of inspiration for future work.
As famous scientist Heinrich Hertz stated, “One cannot escape the feeling that these mathematical formulae have an independent existence and an intelligence of their own, that they are wiser than we are, wiser even than their discoverers, that we get more out of them than we originally put into them.”, presenting groups by generators and relations has been crucial in yielding innovative findings and shedding light on various topics in abstract algebra. Indeed, this paper is part of the contemporary research that shows renewed interest in unlocking its full potential.
2. Preliminary Knowledge
The following definitions build the foundation for the definition and the properties of the free group:
For a set whose elements are “formal” symbols, construct a set by replacing each with the symbol . The “formal” here means that the elements of S and are only symbols with no implied mathematical properties or relations with each other (refer to 2.3).
By placing (juxtaposing) the symbols in S and next to one another, we obtain strings such as and so on. All finite strings of the form where are called words from S, including the empty word e which is the string of no symbol . Define the set of all words from S as .
In order to construct a group out of , we define a binary operation juxtaposition on the set as:
For any and , juxtapose .
We know from
and
that
; thus
, i.e.
is closed under juxtaposition. Then, it is straightforward to show that this operation is associative and the identity element (left and right) is the empty word. The commutative law doesn’t necessarily hold in
because
and
are distinct formal symbols. Also, notice that a word of such form as
doesn’t cancel out to equal
At this point, “group” with operation juxtaposition still lacks a definition of inverses. As stated before, the juxtaposition of a given element a and its intuitive inverse doesn’t equal e. Defined as formal symbols, the individual elements in do not have direct arithmetic inverses. Fortunately, this problem can be solved using the idea of equivalence classes, an approach inspired by a similar limitation in constructing the field of quotients of an integral domain1 [9] .
Theorem 1 (Equivalence Classes of Words): For any pair of elements u and v of , we say that u is related to v if v can be obtained from u by a finite sequence of insertions or deletions of words of the form or , where . This relation is an equivalence relation on and related elements form equivalence classes that partition .
Proof: It suffices to prove that this relation is an equivalence relation on and the partition by equivalence classes follows from Lagrange’s Theorem.
Reflexivity: can be obtained directly from u with no insertions or deletions.
Symmetry: If u is related to v, i.e. v can be obtained from u by some finite sequence Q of insertions or deletions of or ; then, a corresponding sequence Q’ can be created by replacing every insertion in Q with a deletion and every deletion with an insertion. It’s easy to verify that u can be obtained from v by Q’. Also, same as Q, Q’ is a finite sequence of insertions or deletions of or . Hence, v is related to u.
Transitivity: If u is related to v and v is related to w, i.e. v can be obtained from u by some finite sequence Q1 of insertions or deletions of or and w can be obtained from v by some finite sequence Q2 of insertions or deletions of or ; then w can be obtained from u by sequence Q3 where Q3 is the composition of Q1 and Q2, i.e. applying Q3 is equivalent to applying Q1 (which gives v from u) followed by Q2 (which subsequently gives w from v). Clearly, Q3 is still a finite sequence of insertions or deletions of or . Hence, u is related to w.
We now proceed to introduce the formal definition of the free groups and subsequent discussions.
3. Free Groups
3.1. Definition
A free group F of S is defined by the following theorem:
Equivalence Classes Form a Group: Let S be a set of distinct symbols. For any word u in , let denote the set of all words in equivalent to u, i.e. is the equivalence class containing u. Then the set of all equivalence classes of elements of forms a group under the operation .
Proof: Denote the set of all equivalence classes of elements of as F.
Closure: For any and , because for any and .
Associativity: For any and , .
Identity element : Since e is the identity element in , for any , . Therefore, is the identity element in F.
Every element in F has an inverse: For any , because for any . Also, (the identity element) and because and are equivalently related to e by a deletion. Thus, the inverse of any is .
3.2. Key Properties
Observation based on the previous definition of a free group of S as the set of all equivalence classes of elements of under the operation allows us to arrive at the following two properties. These properties show the significance of free groups in group theory and supports discussions later on in the paper.
Proposition 1: Universal Mapping Property
Every group is a homomorphic image of a free group.
Proof: Let G be a group and let S be a set of generators of G (S may be taken as G itself, so such an S always exists). Now, let F be the free group on S. Here, since any word is also an element of G, we need to distinguish between the two cases by notations and (The two elements are different from each other as the operations on F and G are different.) Still, denotes the equivalence class in F to which belongs.
Now consider the mapping given by .
Clearly, f is well defined, because insertions or deletions of words of the form or corresponds to insertions or deletions of the identity in G (since x and represent inverses of each other in G), so that all the elements in the same equivalence class in F correspond to a same element in G. Also, f is onto G because G is generated by S.
Then, we check that f is homomorphic (operation-preserving) by
Proposition 2: Universal Factor Group Property
Every group is isomorphic to a factor group of a free group.
Proof: In fact, this proposition follows as a consequence of Proposition 1 and the First Isomorphism Theorem for Groups2 [10] .
Still, as defined in Proposition 1, let G by a group and let S be a set of generators of G. Now, let F be the free group on S. The mapping given by is a surjective homomorphism. From there, the First Isomorphism Theorem for Groups gives 1) the kernel of f is a normal subgroup of F and 2) by surjectivity.
4. Generators and Relations
4.1. Formal Definition [3]
Let G be a group generated by some set and let F be the free group on A. Let be a subset of F and let N be the smallest normal subgroup of F containing W. We say that G is given by the generators and the relations if there is an isomorphism from F/N onto G that carries to .
The notation for such G is:
*For the sake of convenience in the discussions in this paper, the number of generators and relations in the definition is finite. However, this arbitration is not necessary.
Following the formal definition, free groups can be understood as groups “free” of relations, i.e. (there is no additional relations apart from the identity element and pairs of inverses). Hence, it is easy to show that any subgroup of a free group is still a free group because the set of generators of a subgroup is a subset of the original set of generators, and the fact that these generators have no extra relations remains true for the subgroup.
4.2. Exemplification
Let G and H be groups, and let φ: G → H be a homomorphism. Then:
➢ The kernel of φ is a normal subgroup of G,
➢ The image of φ is a subgroup of H, and
➢ The image of φ is isomorphic to the quotient group G/ker(φ).
In particular, if φ is surjective then H is isomorphic to G/ker(φ).
A rigorous proof of the theorem can be found in [10] .
All definitions established, several problems closely related to the usage of generators and relations will be presented in this section. The course of solving these problems and proving related theorems shows exactly how generators and relations simplify problems and offer interesting, intuitive insights.
4.2.1. D8 (Dihedral Group of Order 16)
By definition, the dihedral group D8 is the group of all symmetries of a regular octagon, i.e. D8 consists of the eight isometric rotations and the eight reflections of a regular octagon. The following work describes a method to obtain its standard algebraic presentation from this geometric definition. One side note for the reason of choosing D8 instead of D4 is that proof for deriving D4’s algebraic presentation can readily be found in a number of papers and teaching materials. Also, the work on D8 can be readily generalized to obtain the algebraic presentation of any .
Let F be the free group on the set , and let N be the smallest normal subgroup of F containing the set . In order to derive the algebraic presentation of D8, our goal here is to show that .
Consider a regular octagon centered at the origin. Let’s begin by constructing the mapping so that a is taken to (a counterclockwise rotation about the center through angle 45˚) and b is taken to (a reflection about the axis through the center that makes an angle 0˚ counterclockwise with the x-axis, i.e. a horizontal reflection). It is straightforward to verify that this mapping is a well-defined homomorphism (D8 is generated by and its operation is composition of plane isometries; refer to 3.2/Proposition 1). Furthermore, because . Thus, by 3.2/Proposition 2.
Now the only work left is to show . Since we know by isomorphic to D8 that has sixteen elements, it suffices for us to show that F/N also has sixteen elements because . With observation, we claim that the set
of left cosets of N is F/N itself.
To validate this claim, first note that every element of F/N can be generated by successive left multiplications on N with various combinations of a’s and b’s. Hence, it suffices to verify that Q is closed under left multiplication by a’s and b’s. The case of left multiplying with a’s is trivial as . For b, we complete the following formulae (note that and by the fact that N is a normal subgroup of G):
where because and applying this process recursively to a total of times gives .
The fact that Q is closed under left multiplication by a’s and b’s gives us that F/N has at most sixteen elements. Meanwhile, since , i.e. is a factor group of F/N, it holds that F/N has at least sixteen elements. Therefore, F/N has the same sixteen elements as and .
In fact, the reasoning argument developed above to prove that the group F/N has sixteen elements is further formalized and generalized by Dyck’s Theorem and its corollary, which can also be proven using the idea of the free group.
Dyck’s Theorem (1882): Let and let , then is a homomorphic image of G.
In other words, Dyck’s Theorem states that if we start with a group G defined in terms of generators and relations and create a group G’ by introducing additional relations on the same set of generators, then G’ is a homomorphic image of G.
Proof: Let F be the free group of the set . Let N be the smallest normal subgroup of F containing and let M be the smallest normal subgroup of F containing . Then, by the definition of generators and relations, and .
Consider the mapping that sends aN to aM for . It is trivial that f is onto F/M due to . Also, f is a homomorphism because . With and , the surjective homomorphism from F/N to F/M induces a surjective homomorphism between G and G’. Hence, G’ is a homomorphic image of G.
Corollary: If K is a group satisfying the defining relations of a finite group G and
, then
.
Proof: By Dyck’s Theorem, we know that K is a homomorphic image of G, which gives . With the condition of , we obtain . Given that K is a homomorphic image of G, we have .
4.2.2. The Quaternion Group Q4
The quaternion group is defined by the presentation . This section seeks to unveil the concrete structure of Q4 given its generators and relations, and the arguments here build on some of the conclusions and theorems presented in 4.2.1.
Again by definition, Q4 is isomorphic to F/N, where F is the free group on the set and N is the smallest normal subgroup of F containing and . Now, if we let and , then it follows from the same argument in 4.2.1 that S is closed under left multiplication by combinations of a’s and b’s. Then, as in 4.2.1, we have .
From there, we can understand the structure of Q4 once we know the structure of the elements in H. The only and very useful information we are left with at this point is the three relations of the generators which define Q4.
First of all, observe that gives . Then gives . Hence, there are at most four elements in H and therefore, at most eight in Q4―namely, .
This seemingly crowning conclusion actually poses a larger uncertainty, as there is one more piece of essential work left―determining whether Q4 has exactly eight elements; in other words, determining whether the eight “elements” of Q4 as listed above are distinct. Clearly, there are examples that satisfy the defining relations but have less than eight elements, such as whose order is only 4.
However, by the Corollary to Dyck’s Theorem proven in 4.2.1, we know that despite negative examples, it suffices to find one specific group G that satisfies the defining generators and relations of Q4 and in order to obtain and therefore . It turned out that there exists such an “example” G generated by the matrices
Calculating all the elements in G directly can prove that its eight elements are all distinct. Therefore, the quaternion group Q4 given by is of order 8, and its elements are of forms . One immediate consequence of this conclusion is that Q4 is not isomorphic to D4 as groups both of order 8.
In fact, the process of understanding Q4 reveals a fundamental shortcoming of defining groups in terms of generators and relations: from there, it is often quite difficult―impossible in certain cases―to come up with the structure of the group in the concrete sense―Cayley tables, Cayley graphs, or even only a list of elements. In fact, even when the “candidate” elements are listed, we must still verify that it is possible for the group to cover the entire magnitude of the list, i.e. there is no duplication of elements in the list. The typical way to do so is by mentioning a specific “example” group that satisfies the defining generators and relations and that is of the same size as the list of elements, so that the result can be affirmed with the help of the Corollary to Dyck’s Theorem.
The approaches and conclusions in 4.2.1 and 4.2.2 will come into play again later in the paper, where these ideas are referred to in further analyzing group structures.
4.2.3. Fun Example: Homophonic Quotients of Free Groups
The following is a fun real-life scenario partly inspired by Mestre et al.’s work Quotient homophones des groupes libres [11] . By applying the mathematical concept to concrete words around us, it offers a relaxing perspective to flow with the idea of generators and relations.
Let G
5. Applications
5.1. Classification of Finite Groups
The first major application of defining groups in terms of generators and relations we will look at is how it serves as a handy tool in classifying finite groups of a certain order. As a first step, we will show how this definition can be used to prove Cayley’s classification theorem of groups of order 8. The primary reason for choosing order 8 among other orders is that the classification process of these is sufficiently instructional in approaching similar topics without the proof becoming overly complicated; meanwhile, the extensive discussion on quaternion group Q4 whose order is also eight offers support in developing the proof. Then, the work will be extended to groups of higher orders considered workable by hand, and we will arrive at a brief classification table of finite groups of orders up to 15.
Classification of Groups of Order 8 (Cayley, 1859): Up to isomorphism, there are only five groups of order 8: , , , D4, and the quaternion group Q4.
Proof: By the Fundamental Theorem of Finite Abelian Groups, we know that any abelian group of order 8 is isomorphic to , , .
Prior to dealing with the non-Abelian cases, we prove the following lemma:
Lemma 1: If every element of a group except its identity has order 2, then the group is Abelian.
Proof: If for every , i.e. , then for every . Hence, for any , , which implies that the group G is Abelian.
Now, consider a non-Abelian group G whose order is 8. Meanwhile, let and .. From previous discussions, we know that and . Therefore, we are left with showing that G must be isomorphic (i.e. satisfy the defining relations of) either G1 or G2.
By Lagrange’s Theorem, the order of some element (not the identity) must divide 8, which is the order of the group itself. This gives that or 4 or 8. By Lemma 1, we know that not all elements of G have order 2. Hence, whose order is 4 or 8. If , then . Therefore, such that . Then, such that (the group generated by a). Such an element b exists because . By Lagrange’s Theorem, we know that .
Consider the element by closure. By cancellation, , ab, a2b, or a3b. What’s more, cannot equal any powers of a, because b2 commutes with b while some power of a doesn’t. Hence, we are left with only two cases: or .
Case 1: .
Note that
because
is a normal subgroup of
Case 2: .
Same reasoning as in Case 1 gives us the conclusion . Then, .
Therefore, G in Case 2 satisfies the defining relations for G2, and the entire classification is complete.
Extension: Classification of Finite Groups Up to Order 15
This convenient way of classifying groups of order 8 using generators and relations presentation is fundamental to understanding more complicated group structures. Used in combination with other theorems that teach us about the order of elements in groups of orders p2, 2p, or pq where p and q are primes, analyzing generators and their relations allows us to classify groups of orders up to 15. The complete process will not be elaborated in this paper. There is one more note when it comes to groups of order 12: There are also 5 groups up to isomorphism of order 12; apart from , , and familiar to us, the additional group Q6 called the dicyclic group of order 12, has presentation . Indeed, the dicyclic groups are the generalization of the quaternion group in higher orders, a property that can also be explored and developed favorably using generators and relations.
Table 1 lists the classification of groups of every order up to 15; with further knowledge of group structures including Sylow’s Theorems, this classification table can be further extended to explore groups of higher orders.
5.2. Geometric Realization of Dihedral Groups with Mirrors
Indeed, defining groups by generators and their relations has a highly intuitive nature; particularly when it comes to dihedral groups, as is evidenced by their general structure of presentation already well-studied. On that basis, this section
Table 1. Classification of finite groups of every order up to 15.
will be presenting a special way of realizing the dihedral groups―using reflections visualized by mirrors; and reflections in only one single pair of mirrors on the plane can realize any finite or infinite dihedral group.
Consider finite dihedral groups first. Taking D4 as an example, we first place a pair of mirrors A and B facing each other such that they make a 45˚ angle counterclockwise in between. Let a denote a reflection in mirror A and b a reflection in mirror B. If we adjust mirror A to be horizontal in direction, we can then easily verify that (a reflection about the axis through the center that makes an angle 0˚ counterclockwise with the x-axis, i.e. a horizontal reflection; refer to 4.2.1) and (the combined effect of first applying a followed by b; written conveniently as ba) = (a counterclockwise rotation about the center through angle 90˚; refer to 4.2.1). Hence, ba and a correspond to the two generators of D4. Because the defining relations of a dihedral group follows directly from the geometric meanings (i.e. rotation and reflection about a certain axis or angle) of its generators, it is straightforward to show that . Added the fact that the set of the eight distinct positions in the figure is closed under reflections a and b, we have D4 represented in Figure 1.
From this example, we see that the key in constructing the two mirrors is finding the two generators of Dn (the single reflection and the smallest rotation
along a angle) and verifying the three relations. The reflection is given
right away; and it can be shown that the effect of is always a rotation along twice the angle in between the two mirrors.
Figure 1. The Group D4 represented as reflections in mirrors at a 45˚ angle.
This piece of insight allows us to generalize the case to all finite dihedral groups Dn and eventually, to D∞ in the limiting case. By the previous argument, any given group Dn corresponds to all the reflections in a pair of mirrors set at
an angle of . Figure 2 illustrates a portion of D180 thus produced by two mirrors that make a 1˚ angle.
As n approaches infinity, the angle between mirrors approaches zero, i.e. the mirrors become parallel to each other in the case of D∞, illustrated in Figure 3.
5.3. Knot Groups3
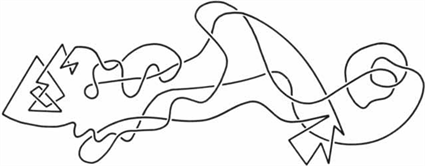
The last application of presenting groups by generators and relations to be discussed in this paper is its role in the branch of knot theory. The strict mathematical definition of knots is a one-dimensional curve situated in ordinary three-dimensional space such that it begins and ends at the same point and does not intersect itself. One way to picture the concept a little more concretely is by thinking of the curve as a looped string―and indeed, hand-tied knots, its diagrams, and even characteristics such as minimum number of crossing points bear a great deal of physical intuition (Figure 4).
However, the fundamental problem of whether certain knots are equivalent is extremely hard to solve with geometry alone, because there is always an infinite number of possible ways to deform a given knot into different physical “appearances”. Therefore, it is necessary to identify some property that distinguishes between knots that are not equivalent. In knot theory, such a property of knots is called invariant. While physical invariants such as minimum number of crossing points are sometimes hard to determine, according to Lee Neuwirth [12] , the algebraic invariant―knot group―“comes incredibly close to giving a complete classification.”
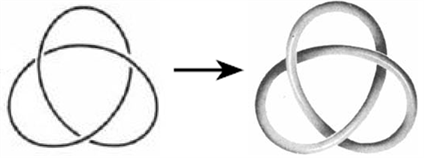
In the following section, we will study the construction of the knot group of one of the most basic knots―the trefoil knot (illustrated in Figure 5) in detail. This process offers new perspectives to understanding 1) how group presentation
Figure 2. The Group D180 represented as reflections in mirrors at a 1˚ angle.
Figure 3. The Group D∞ represented as reflections in parallel mirrors.
Figure 4. Example of a Knot.
Figure 5. The Trefoil Knot (simple line solid tube).
solid tube).
using generators and relations arises naturally in describing special topic areas such as knot theory and 2) mathematical manipulations and conclusions based on this system of group presentation. The very origin of such ideas shall be credited to French mathematician Henri Poincaré.
An accessible definition of two knots being equivalent requires considering each knot thickened slightly into a tube-like, solid figure. The knots are equivalent if and only if the shape of one can be obtained by deforming the other―pulling, pushing or twisting its tube model without breaking it or crossing it through itself. (Side Note: Certain knots known as “wild knots” cannot be thickened and modeled in such manner, but as they are not dealt with in general knot theory, they are not in the scope of this paper.) In this sense, the property of a knot is essentially the way it is embedded in three-dimensional space. Therefore, knots can be distinguished by characterizing all the possible ways of moving through the three-dimensional space without “running into” a given knot solid itself.
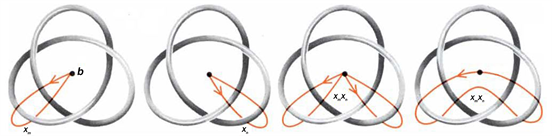
For the convenience in examining such possible pathways, let’s call the three-dimensional space outside a given knot tube S. Let Ω be the set of all directed, one-dimensional paths in S (thus avoiding the knot tube) that begin and end at a fixed point b in S. Point b can be chosen arbitrarily, since the pathways by which a knot group is defined are not altered by the choice of any specific points. The one-dimensionality makes sure that there are no knots on the pathways because any knot will deform to a single point in one-dimensional space. Also, the “trivial” path e that doesn’t leave b is count in Ω as well. Some elements of Ω are illustrated in Figure 6.
Observe that in terms of their relationships with the knot, λ is equivalent to e, as the length of λ does not affect its spatial interaction with the knot. Also, β can be untwisted into δ, and the knot at the tip of α can deform and the resulting path will also be equivalent to δ. On the other hand, λ is clearly not equivalent to δ, as δ loops round the knot once while λ doesn’t. With that knowledge, the following equivalence relation can be defined on Ω as
For , x is equivalent to y if and only if x can be deformed into y.
where the deforming process can include pulling, pushing, unknotting, or even crossing the path over itself, but neither the starting point nor the ending point may be moved and the path may not be broken into disjoint segments, moved cross the knot tube, or moved outside of S.
The proof that this above relation is indeed an equivalence relation follows quite trivially from the definition. In fact, such deformations are called homotopies in knot theory, and paths that differ only by homotopies are called homotopic. Hence, Ω is partitioned into equivalence classes where denotes the set of all elements in Ω homotopic to path . Then, in the same manner as free groups were defined in section 3.1, we can define the underlying set of the knot group as the set of all equivalence classes in Ω and its group operation as where represents the path from point b that first follows back to b and then follows back to b. As illustrated in Figure 7, and is well-defined. Hence, the set of all equivalence classes in Ω is closed under this operation.
Figure 6. All black paths are homotopic, while the colored paths are not homotopic to the black ones or to one another.
Figure 7. The group operation of the knot group.
Similar graphic illustrations easily show that the operation is associative but not necessarily commutative. Also, the identity element is the equivalence class containing the trivial path by for all in the set, and the inverse of , , is defined as where is the path in Ω that has the same shape but the opposite direction as . As illustrated in Figure 8, , so .
Because of the limited knowledge of knot theory developed in this paper, the rigorous proof that the knot group is indeed an invariant will be omitted. However, intuition for this conclusion can be partly obtained by considering how the knot group changes when the corresponding knot tube is deformed into other equivalent ones. Through deformation in three-dimensional space, all pathways in S of the first knot tube would change into pathways in S’ of the resulting knot tube with their relationship with the knot tube unchanged. That is to say, any pair of homotopic pathways stays homotopic through the deformation process by the definition. And since such deformation is always reversible, the knot groups of the original and the resulting knots are equal.
The next step is to derive the precise presentation of the trefoil knot group―i.e. its generators and relations. To begin with, observe that all pathways that loops round the same segment of the trefoil are equivalent, where by segment I mean the part taken from one crossing (underpass) point to the next. Figure 9 illustrates the three segments, and it can be easily verified that the products of (illustrated in Figure 10, where the three segments are
Figure 8. The inverse of a path.
Figure 9. The three segments of the trefoil.
Figure 10. The generators of the trefoil knot group.
shaded with different colors) and their inverses cover all equivalence classes in Ω. Thus, are the generators of the knot group.
Then, to obtain relations, consider the interactions between
and
. Because the three of them are defined in terms of their locations on the segments, the only places where they meet one another are at the three crossing (underpass) points. Take the upper left crossing point in the trefoil as an example: observe that pulling the starting and ending point of path x along path
Figure 11. The relations in knot groups.
. Back in 1910, German mathematician Max Dehn proved that the knot group is calculable, which means that a group presentation with generators and relations can always be obtained for any given knot [13] . And for knots not too “wild”, the method described in the paper can be generalized to construct knot groups in other cases.
Now that physical knots are transformed into pure algebra, some substitution and manipulation in the relations can be made. It is evident that , as a product of and , can be eliminated, and that gives another equivalent presentation of the trefoil knot group: . From this form of the relation, we can further develop a third presentation where the relation is written in exponent form by letting and . The presentation is valid because any product of and their inverses can be expressed as products of and their inverses, verified as and .
The above discussion vividly displayed the fascinating flexibility of the knot group; however, challenge remains that a given knot group may have several different-looking group presentations, and lengthy, complicated relations are often quite hard to simplify and reduce. Also, given a group presentation, it is not at all evident what the original knot looks like (a problem similar to that in section 4.2). Nevertheless, the knot group still offers key insights that are hardly attainable through the physical tools. For example, if we look at the trivial knot―basically a simple loop as illustrated in Figure 12―its knot group is just the group presented with only one generator and no relations. On the other hand, the process of constructing knot groups tells us that tying more knots meant adding more crossing points and thereby, creating a knot group that has more generators and more complicated relations than the original group. This
Figure 12. The trivial knot.
simple investigation allows us to handily answer one important question in knot theory which asks whether tying a second knot can untie an existing one (i.e. Can their product be the trivial knot?) By noting that the resulting knot group must be more complicated than the one we started with, we can conclude that the resulting knot group cannot be equal to the trivial knot group which is the simplest in structure. Thus, it’s impossible to untie a knot by tying another.
Countless mathematical work exists out there that investigates the usage of knot groups and the idea of generators and relations as a whole. The main body of this paper will end here, and the author hopes that the above discussions illustrate a basic understanding of how generators and relations are constructed and put into use.
6. Conclusions
Since the basic structure of this paper has already been summarized in the abstract and the introduction, I would like to conclude the entirety of my work by elaborating a little more on some advantages and disadvantages of presenting groups in terms of generators and relations.
As is briefly touched in this paper, many topics―knot theory and algebraic topology in particular―are understood much more naturally through groups defined by generators and relations. This is because such definition captures more direct and accurate information while allowing great freedom for individual elements in the given group. Furthermore, within the field of group theory, it is routinely easier to construct examples and counterexamples with generators and relations by the same reason.
On the other side of the coin, the main disadvantage of relying too heavily on generators and relations is the ambiguity of the precise form of the group―given its presentation, it is often extremely hard to determine the size of the group, find out its identity element, or even tell whether the group is finite or not (as illustrated in the example of the quaternion group). Meanwhile, a given group has infinitely many completely different presentations in terms of generators and relations (as illustrated in the case of the knot group). Fortunately, however, with today’s rapid advancement of computer technologies, this ambiguity from generators and relations is gradually being removed while their strength can be made better use of.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Zhou, T.C. (2018) The Power of Group Generators and Relations: An Examination of the Concept and Its Applications. Journal of Applied Mathematics and Physics, 6, 2425-2444. https://doi.org/10.4236/jamp.2018.611204
References
- 1. Sir Hamilton, W.R. (1856) Memorandum Respecting a New System of Roots of Unity. Philosophical Magazine, 12, 446. https://doi.org/10.1080/14786445608642212
- 2. von Dyck, W. (1882) Gruppentheoretische Studien. Mathematische Annalen, 1882, 1-44. https://doi.org/10.1007/BF01443322
- 3. Nielsen, J. (1924) Die Isomorphismengruppe der freien Gruppen. Mathematische Annalen, 91, 169-209. (In German) https://doi.org/10.1007/BF01556078
- 4. Gallian, J. (1986) Contemporary Abstract Algebra. 8th Edition, Cengage, Belmont, CA, 451.
- 5. Holt, D. (2013) Presentation of Groups. The University of Warwick Math, 10-31.
- 6. Birman, J., Ko, K. and Lee, S. (1998) A New Approach to the Word and Conjugacy Problems in the Braid Groups. Advances in Mathematics, 139, 322-353. https://doi.org/10.1006/aima.1998.1761
- 7. Belabas, K. and Gangl, H. (2004) Generators and Relations for K2OF. K-Theory, 31, 195-231. https://doi.org/10.1023/B:KTHE.0000028979.91416.00
- 8. Rustom, N. (2016) Generators and Relations of the Graded Algebra of Modular Forms. The Ramanujan Journal, 39, 315-318. https://doi.org/10.1007/s11139-015-9674-z
- 9. Schwarzweller, C. (1998) Section IV. 21. The Field of Quotients of an Integral Domain (Revised 2014/11). East Tennessee State University Math, 1. http://faculty.etsu.edu/gardnerr/4127/notes/IV-21.pdf
- 10. Omar, M. (2014) Lecture Notes Isomorphism Theorem Proofs. Math 171, Harvey Mudd College, 1.
- 11. Mestre, J.-F., Schoof, R., Washington, L. and Zagier, D. (1993) Quotient homophones des groupes libres. [Homophonic Quotients of Free Groups.] Experimental Mathematics, 2, 153-155. https://doi.org/10.1080/10586458.1993.10504275
- 12. Neuwirth, L. (1979) The Theory of Knots. Scientific American, 240, 110-124. https://doi.org/10.1038/scientificamerican0679-110
- 13. James, I.M. (1999) History of Topology. Elsevier, Amsterdam, 302-324.
NOTES
1In constructing the field of quotients of an integral domain, the similar problem arises where the inverse of formal symbols cannot be because their product, , was also a formal symbol that does not cancel into the identity. The main material that shed light on solving the problem is [9] Christoph Schwartzweller’s work The Field of Quotients over an integral domain.
2The First Isomorphism Theorem for Groups states the following:
3Figures in this section except Figure 9 are adapted from [12] .