Journal of Applied Mathematics and Physics
Vol.04 No.06(2016), Article ID:67824,14 pages
10.4236/jamp.2016.46119
A Numerical Method for Nonlinear Singularly Perturbed Multi-Point Boundary Value Problem
Musa Çakır, Derya Arslan
Department of Mathematics, Faculty of Science, University of Yuzuncu Yil, Van, Turkey

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 April 2016; accepted 26 June 2016; published 29 June 2016
ABSTRACT
We consider a uniform finite difference method for nonlinear singularly perturbed multi-point boundary value problem on Shishkin mesh. The problem is discretized using integral identities, interpolating quadrature rules, exponential basis functions and remainder terms in integral form. We show that this method is the first order convergent in the discrete maximum norm for original problem (independent of the perturbation parameter ε). To illustrate the theoretical results, we solve test problem and we also give the error distributions in the solution in Table 1 and Figures 1-3.
Keywords:
Singular Perturbation, Fitted Finite Difference Method, Shishkin Mesh, Nonlocal Boundary Condition, Uniform Convergence

1. Introduction
In this paper we shall consider singularly perturbed multi-point nonlinear problem
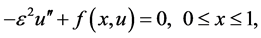 (1)
(1)
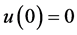 (2)
(2)
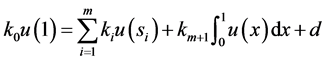 (3)
(3)
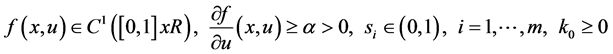
where, 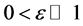 is small perturbation parameter. The solution u(x) has boundary layers at
is small perturbation parameter. The solution u(x) has boundary layers at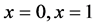 .
.
Singularly perturbed differential equations arise many applications such as, fluid mechanics, chemical-reactor theory, the Navier-Stokes equations of fluid flow at high Reynolds number, control theory, electrical networks, and other physical models. In recent years, singularly perturbed differential equations were studied by many authors in various fields of applied mathematics and engineering. For examples, Cziegis [1] studied the numerical solution of singularly pertürbed nonlocal problem. Cziegis [2] analyzed the difference schemes for problems with nonlocal conditions. Bakhvalov [3] investigated on optimization of methods for solving boundary-value problems in the presence of a boundary layer. Amiraliyev and Çakır [4] applied the difference method on a Shishkin mesh to the singularly perturbed three-point boundary value problem. Amiraliyev and Çakır [5] researched a uniformily convergent difference scheme for singularly perturbed problem with convective term end zeroth order reduced equation. Amiraliyev and Çakır [6] studied numerical solution of the singularly perturbed problem with nonlocal boundary condition. Amiraliyev and Duru [7] estimated a note on a parameterized singular perturbation problem. Amiraliyev and Erdoğan [8] studied uniform method for singularly perturbed delay differential equations. Amiraliyeva, Erdoğan and Amiraliyev [9] applied a uniform numerical method for dealing with a singularly perturbed delay initial value problem. Adzic and Ovcin [10] studied nonlinear spp with nonlocal boundary conditions and spectral approximation. Amiraliyev, Amiraliyeva and Kudu [11] applied a numerical treatment for singularly perturbed differential equations with integral boundary condition. Herceg [12] studied the numerical solution of a singularly perturbed nonlocal problem. Herceg [13] researched solving a nonlocal singularly perturbed problem by splines in tension. Çakır [14] studied uniform second-order difference method for a singularly perturbed three-point boundary value problem. Geng [15] applied a numerical algorithm for nonlinear multi-point boundary value problems.
In this study we present uniformly convergent difference scheme on an equidistant mesh for the numerical solution of the problem (1)-(3). The difference scheme is constructed by the method integral identities with the use exponential basis functions and interpolating quadrature rules with the weight and remainder terms in integral form [5] - [7] . In Section 2, the asymptotic estimations of the problem (1)-(3) are established. The difference scheme constructed on Shishkin mesh for numerical solution (1)-(3) is presented in Section 3 and in Section 4. We prove that the method is first-order convergent in the discrete maximum norm. In Section 5, a numerical example is considered. The results show that the uniform finite difference method on Shishkin mesh is more powerful method than other methods for nonlinear singularly perturbed multi-point boundary value problem.
2. The Continuous Problem
In this section, we describe some properties of the solution of (1) with Lemma 2.1. we use 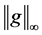 for the continuous maximum norm on the [0, 1], where
for the continuous maximum norm on the [0, 1], where 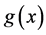 is any continuous function.
is any continuous function.
Lemma 2.1.
Let 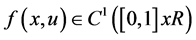 and
and 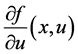 is uniformly bounded in
is uniformly bounded in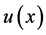 . We assume that
. We assume that
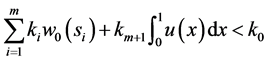 (4)
(4)
where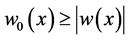 ,
,
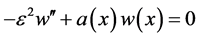 (5)
(5)
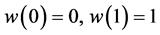 (6)
(6)
solution of this problem.
So, the solution of the Equation (1) satisfies the inequalities

and

where, C0 and C are constants independent of ε.
Proof. We rewrite the Equation (1). Hence, we use intermediate value theorem for
where 

Consequently, we obtain the following linear equation,

Now, let 
We can write the solution of the Equation (9) as follows



where 
First, we prove the estimate

Second, we prove the estimate

According to the Equation (4), λ is a finite number. Then, from the Equations (13), (14) we have the following inequality

we now prove the estimate the Equation (8).
If 

and from the Equation (16)

Now, we take derivative of the Equation (9) and if it called


Now, we proceed with the estimation of

We use the following relation for

where
the Equation (21) with the values 

In a similar manner, the Equation (21) with the values 

We write the solution of the Equations (18), (19) in the form,
where 



According to the maximum principle in the Equations (24), (25), we can the following Barrier function,
This Barrier function provides the conditions of the maximum principle and
In a similar manner, according to the maximum principle in the Equation (26), we can write
where 


where 


after some arragement, we can obtain,

Finally, from
which leads to the Equation (8).
3. Discretizaton and Non-Uniform Mesh
Let us consider the following any non-uniform mesh on
We present some properties of the mesh function 



Now, We will construct the difference scheme for the Equation (1). First, we integrate the Equation (1) over 

where 






If we rearrange the Equation (31) it gives

After doing some calculation

where

and
So, from the Equation (37), the difference scheme is defined by

Now, we define an approximation for the second boundary condition of the Equation (1). We accepted that 


where remainder term

By neglecting 




We will use the Shishkin mesh to be e -uniform convergent of the difference scheme the Equations (42)-(44). So the Shishkin mesh divides each of the interval 






if 





where, N is even number, 
4. Error Analysis
Let 




where 
Lemma 4.2. Let 




Proof. We evaluate the Equation (38) and the Equation (41), respectively
Consequently,

In the beginning, we consider the case 

it then follows from the Equation (50) that

Second, we consider the case 


and 
In the seperate 

In the seperate

where for
and so

Analogously for 
thus

according to the Equation (54) and the Equation (55), we can rewrite the the Equation (53)

In the seperate 

The last estimate is for 

We rewrite the the Equation (50) for 

We take integrate in the Equation (58) and so

where


we rewrite the Equation (59) with the Equation (60) and the Equation (61), thus,

where
We use in a similar way as above for 

Next, we use estimate for the remainder term r:
From the Equation (41) we can write
from the Equation (8)

Lemma 4.3. Let zi be solution of the Equations (45)-(47). Then there is the following inequality,

Proof. Rearranging the Equation (45) gives
where
according to the proof of Lemma 2.1, we can use the maximum principle, and so it is easy to obtain,

Conclusion 4.1. We know that the solution of the Equations (1)-(3) is 


5. Numerical Example
In this section, an example of nonlinear singularly perturbed multi-point boundary value problem is given to illustrate the efficiency of the numerical method described above. The example is computed using maple 10. Results obtained by the method are compared with the exact solution of example and found to be good agreement with each other. We compute approximate errors



Example 5.1.
We solve the difference scheme the Equations (42), (44) using the following iteration technique,



where
The system of the Equations (68)-(70) is solved by the following procedure,
It is easy to verify that
For this reason, the described procedure above is stable. Also, the Equations (42)-(44) has only one solution.
Now, we consider the following test problem,



which has the exact solution,
In the computations in this section, we will take 

The error estimates are denoted by
and
The convergence rates are
The numerical results obtained from the problem of the difference scheme by comparison, the error and uniform rates of convergence were found and these are shown in Table 1. Consequently, numerical results show that the proposed scheme is working very well.
The results point out that the convergence rate of the established scheme is really in unision with theoretical analysis.
From the graps it is show that the error is maximum near the boundary layer and it is almost zero in outer region in the Figure 3. Approximate solution compared with exact solution in Figure 2. Approximate solutions are given for different values of ε in Figure 1.
Table 1. The computed maximum pointwise errors eN and e2N , the numerical rate of convergence pN on the Shishkin mesh 
Figure 1. Approximate solution distribution for ε = 2−4, 2−6, 2−8, 2−10 using N = 256.
Figure 2. Comparison of approximate solution and exact solution for ε = 2−14.
Figure 3. Error distribution for ε = 2−2, 2−8, 2−10, 2−12 using N = 256.
6. Conclusion
Consequently, the aim of this paper was to give uniform finite difference method for numerical solution of nonlinear singularly perturbed problem with nonlocal boundary conditions. The numerical method was constructed on Shishkin mesh. The method was pointed out to be convergent, uniformly in the ε-parameter, of first order in the discrete maximum norm. The numerical example illustrated in practice the result of convergence proved theoretically.
Cite this paper
Musa Çakır,Derya Arslan, (2016) A Numerical Method for Nonlinear Singularly Perturbed Multi-Point Boundary Value Problem. Journal of Applied Mathematics and Physics,04,1143-1156. doi: 10.4236/jamp.2016.46119
References
- 1. Cziegis, R. (1988) The Nümerical Solution of Singularly Pertürbed Nonlocal Problem. Lietuvos Matematikos Rinkinys, 28, 144-152. (In Russian)
- 2. Cziegis, R. (1991) The Difference Schemes for Problems with Nonlocal Conditions. Informatica (Lietuva), 2, 155-170.
- 3. Bakhvalov, N.S. (1969) On Optimization of Methods for Solving Boundary-Value Problems in the Presence of a Boundary Layer. The Use of Special Transformations in the Numerical Solution of Bounary-Layer Problems. Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, 9, 841-859.
- 4. Amiraliyev, G.M. and Cakir, M. (2007) Numerical Solution of a Singularly Perturbed Three-Point Boundary Value Problem. International Journal of Applied Mathematics, 84, 1465-1481.
- 5. Amiraliyev, G.M. and Çakir, M. (2000) A Uniformily Convergent Difference Scheme for Singularly Perturbed Problem with Convective Term End Zeroth Order Reduced Equation. International Journal of Applied Mathematics, 2, 1407-1419.
- 6. Amiraliyev, G. M. and Çakir, M. (2002) Numerical Solution of the Singularly Perturbed Problem with Nonlocal Boundary Condition. Applied Mathematics and Mechanics (English Edition), 23, 755-764.
http://dx.doi.org/10.1007/BF02456971 - 7. Amiraliyev, G.M. and Duru, H. (2005) A Note on a Parameterized Singular Perturbation Problem. Journal of Computational and Applied Mathematics, 182, 233-242.
http://dx.doi.org/10.1016/j.cam.2004.11.047 - 8. Amiraliyev, G.M. and Erdogan, F. (2007) Uniform Numerical Method for Singularly Perturbed Delay Differential Equations. Computers & Mathematics with Applications, 53, 1251-1259.
http://dx.doi.org/10.1016/j.camwa.2006.07.009 - 9. Amiraliyeva, I.G., Erdogan, F. and Amiraliyev, G.M. (2010) A Uniform Numerical Method for Dealing with a Singularly Perturbed Delay Initial Value Problem. Applied Mathematics Letters, 23, 1221-1225.
http://dx.doi.org/10.1016/j.aml.2010.06.002 - 10. Adzic, N. and Ovcin, Z. (2001) Nonlinear Spp with Nonlocal Boundary Conditions and Spectral Approximation. Novi Sad Journal of Mathematics, 31, 85-91.
- 11. Amiraliyev, G.M., Amiraliyeva, I.G. and Kudu, M. (2007) A Numerical Treatment for Singularly Perturbed Differential Equations with Integral Boundary Condition. Applied Mathematics and Computations, 185, 574-582.
http://dx.doi.org/10.1016/j.amc.2006.07.060 - 12. Herceg, D. (1990) On the Numerical Solution of a Singularly Perturbed Nonlocal Problem. Univ. u Novom Sadu Zb. Rad. Prirod.-Mat. Fak. Ser. Mat., 20, 1-10.
- 13. Herceg, D. (1991) Solving a Nonlocal Singularly Perturbed Problem by Splines in Tension. Univ. u Novom Sadu Zb. Rad. Prirod.-Mat. Fak. Ser. Mat, 21, 119-132.
- 14. Çakir, M. (2010) Uniform Second-Order Difference Method for a Singularly Perturbed Three-Point Boundary Value Problem. Hindawi Publising Corporation Advances in Difference Equations, Vol. 2010, 13 p.
- 15. Geng, F.Z. (2012) A Numerical Algorithm for Nonlinear Multi-Point Boundary Value Problems. Journal of Computational and Applied Mathematics, 236, 1789-1794.
http://dx.doi.org/10.1016/j.cam.2011.10.010

























































