Received 20 February 2016; accepted 25 April 2016; published 29 April 2016

ABSTRACT

Corresponding to Oswatitsch’s Mach number independence principle the Mach number of hypersonic inviscid flows, 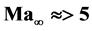, does not affect components of various non-dimensional formulations such as velocity and density, pressure coefficients and Mach number behind a strong shock. On this account, the principle is significant in the development process for hypersonic vehicles. Oswatitsch deduced a system of partial differential equations which describes hypersonic flow. These equations are the basic gasdynamic equations as well as Crocco’s theorem which are reduced for the case of very high Mach numbers,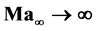. Their numerical solution can not only result in simplified algorithms prospectively utilized to describe the flow around bodies flying mainly in the lower stratosphere with very high Mach numbers. It also offers a deeper understanding of similarity effects for hypersonic flows. In this paper, a solution method for Oswatisch’s equations for perfect gas, based on a 4-step Runge-Kutta-algorithm, is presented including a fast shock-fitting procedure. An analysis of numerical stability is followed by a detailed comparison of results for different Mach numbers and ratios of the specific heats.

Keywords:

Oswatitsch, Mach Number Independence, Bow Shock, PDE, Time Dependent Solution, Ratios of Specific Heats

1. Introduction

Depending on the type of flight vehicle configuration and its mission, the atmospheric re-entry into the earth’s atmosphere takes place at Mach numbers between 20 and 30 [8] . In order to analyse the flow properties around these vehicles at such high Mach numbers, a sufficiently validated data base is required. Existing ground test facilities cannot represent physically and chemically fully correct conditions at such high Mach numbers because of the large number of similarity parameters, whose simultaneous compliance is often contradictory [7] . Considering the similarity parameters in particular, current facilites are able to produce max. Mach numbers in the range of 8 and 10 only [13] . Here, Oswatitsch’s Mach number independence principle explains why above a sufficiently high Mach number, for blunt bodies and behind a strong shock with, some aerodynamic properties (such as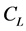, , 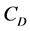, , 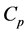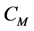relative velocities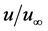, , 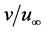the bow-shock stand-off distance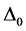, the patterns of streamlines and Mach lines) become independent of 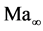[15] .

However, having applied this approach in the 70s’s of the last century to the US space-shuttle, essential differences in the pitching moment between the wind tunnel test results and the data from the first flight occured. The assumed simplifications in terms of high-temperature real gas effects in the model were especially considered to be the reason for these inaccuracies.

In connection with his similarity law and basing on the gas dynamic equation and Crocco’s theorem, Oswatitsch deduced a system of partial differential equations to calculate the flow field around hypersonic vehicles in the limiting case of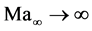. The equations are derived for calorically perfect gas and inviscid flows (see [15] ) and are supplemented with the according boundary conditions. Although the Mach number principle itself is very common in hypersonics, no detailled numercial solution of Oswatitsch’s system of equations has been presented, so far. Based on these equations’ solutions, general similarities between the body and the bow shock could be determined enabling the provision of more accurate initial solutions for advanced algorithms, e.g. a coupled Euler/second-order boundary-layer method [10] .

In order to analyze the equations numerically, we first extent Oswatitsch’s steady partial equations to unsteady conditions and classify them. This is presented in Section 2. It should be clarified if a time-dependent method can be applied. The required boundary conditions as well as the shock determination method and notes regarding artificial viscosity are decribed in Section 3. A brief explanation of the implemented code and some numerical results of selected cases are presented in Section 4 and 5.

2. Governing Equations

Oswatitsch derived a system of equations, consisting of the basic gasdynamic equation and Crocco’s theorem for 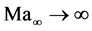under steady conditions only [15] . Due to numerical issues with the calculation of blunt-body- problems in [17] , we want to apply a multi-step Runge-Kutta-algorithm as solution method. Therefore, it is necessary to develop a time-dependent formulation for Oswatitsch’s equations. For simplicity reasons, we only present the 2D-case. The extension to 3D is straight forward.

The derivation of the steady-state Oswatitsch equations is documented e.g. in [7] or [15] . The inclusion of time derivatives-which is a new approach in the derivation of Oswatitsch’s formulation-leads to the following system of partial differential equations [12] :

(1)

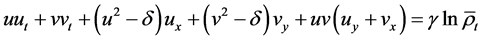(2)

with

which are completed by the expression for the entropy change between two states, , of a calorically perfect gas relating density, entropy and velocity:

(3)

Equation (1) is Crocco’s theorem under the condition of an homenthalp flow, meaning that the total enthalpy is constant in the entire flow field and so. Equation (2) represents the gas dynamic equation in the unsteady case which is derived from continuity and momentum equations.

For a detailed analysis, we non-dimensionalize as follows:

We introduce Equations (1) and (2) yielding

(4)

(5)

(6)

with

Thus, Oswatitsch’s system of partial differntial equations is transfered in a format which allows the determination of its type. We reshape and define the vector as follows

(7)

to receive a general form for Equations (4)-(6)

(8)

For our investigation, it is sufficient to consider only I in Equation (8) to evaluate the type. The matrix I is

(9)

and its eigenvalues can be calculated by solving the characteristic polynom which in this case yields

(10)

(11)

(12)

for the eigenvalues. As is valid in the entire flow field behind the shock all three eigenvalues are positive. In consequence, the derived system of equations is hyperbolic in terms of time and can be calculated with the proposed Runge-Kutta-method. A description of the treatment for parabolic or elliptic types can be found e.g. in [5] or [6] .

3. Boundary Conditions, Numerical Viscosity and Shock Fitting

The method of evalutating and approximating the values at the boundaries is discussed in the following part. Different results, stability and convergence rate are often closely related to the kind that the boundary conditions are set [1] . In the 2D-case four boundaries determine the flowfield, see Figure 1.

1) The first boundary condition is at the bow shock. Here the Rankine-Hugoniot-conditions determine the values of the variables just behind it (index 2). A detailed derivation of the corresponding equations can be found in [7] . All variables depend on the free stream Mach number, the ratio of specific heats and the shock angle, which is the angle between the shock plane’s tangency and the vector of the free stream velocity,

(13)

(14)

(15)

Different values for can be considered to simulate the thermal excitation of the gas. In this paper, we do not distinguish between the gas dynamic state in the flow region ahead and behind the bow shock. So, the value for the isentropic exponent is assumed to remain constant in the entire flow field also for. An effective isentropic exponent is not applied. For Equation (15) no limiting value exists. Thus, we define as the difference between the entropy increase between an oblique and a normal shock. That means that is equal to zero at the position where the shock front is normal to the free stream. With this trick Oswatitsch [4] obtained an expression for the entropy increase across shock waves resulting in the desired limiting value. Under Oswatitsch’s assumptions Equations (13)-(15) simplify to the following set of boundary conditions at the shock

(16)

(17)

(18)

Figure 2 describes the mentioned parameters in this limiting case: in Figure 2(a) and in Figure 2(b) depend on both: the shock angle and the ratio of the specific heats. This does not hold for the entropy. As can be seen in Figure 2(c) the entropy is independent of this ratio. The only oberservable dependency is in terms of the shock angle.

2) The second boundary is at the symmetry line. Here, the usual and well known boundary conditions are implemented, see [2] .

3) The determination of the values at the outlet is just a simple extrapolation. This is allowed as long as the local Mach number at this boundary is larger than 1. Therefore, it is necessary to create a flow field which is extended enough to allow an acceleration to supersonic velocities. This is obviously closely connected to the body contour which is to be investigated.

4) The wall boundary is that the velocity normal to the wall must be zero. Normally, the calclulated velocity at the wall will not satisfy this condition. Thus, it is necessary to modify the velocity vector and the other flow variables at the wall. To accomplish this, a finite one-dimesional compression or expansion wave is emited from the body surface. This wave needs to have a sufficient strength to cancel the normal component of the velocity [2] .

Among others, Pulliam presents in [16] a model of implementing artificial viscosity. His algorithm is succesfully utilized to avoid oscillations and to bring the entire calculation to convergence and a steady state. This is required when spatial derivatives are discretized as central differences. The added dissipation consists of two kinds of viscosity. The first is of second order and should increase its value near shocks. The second is of fourth order. It should stabilize the calculation in the whole flow field. The distinction between both is controlled pressure-related. At this stage, we waive to present the entire algorithm for the determination of the dissipative terms as it is explained very much in detail in [16] . It is to be mentioned that in contrast to Pulliam’s suggestions for the disspipation factors (,), we could only achieve stabile calculations and results with the usage of the following values which were also used by Lecheler [11] . These are four times larger than Pulliam’s proposal:

The investigated body contour does not lead to the occurance of interior shocks. That is why the value for does not affect the solution’s accuracy. However, for consistency reasons we also apply the larger value for.

In order to decrease computational costs it is possible to calculate just the flowfield between the bow shock and the body surface. Position and shape of the bow shock have then to be adapetd to the current conditions in the flow field. This method is called shock-fitting. After each iteration the pressure just behind the shock can be calculated by

(19)

and are determined by extrapolating the flow properties from the interior flow field. The Rankine- Hugoniot condition for curved shocks is

(20)

Equating Equations (18) and (19) provides the horizontal Mach number in front of the shock that bases on the calculations from the interior of the flow field.

(21)

is then brought in relation to the actual Mach number, which for simplicity is taken as horizontal only. With as the speed of sound and as a relaxation factor the distance of each point of the shock plane has to be repositioned and can be calculated with

(22)

For time-asymptotic calcualtions the term will tend to zero after a certain number of iterations and the distance each shock point is moved will become zero as well. In that way the final position of the shock wave ahead of the body is determined. Typical values of are of the order of. Higher values are allowed, but in return the step size between two iteration steps of the movement of the shock has to be increased. By using the complete 4-step Runge-Kutta-procedure, additional smooting functions for the shock plane as presented in [4] are not required.

4. Implemented Algorithm, Grid Dependency and Residuum

The derived unsteady system of equations (see Section 2) can be solved by different approaches. We decided to use an explicite form of the equations wherein the time derivatives at time n are determined by the flow properties at the same time. The equations are then

(23)

(24)

(25)

Spatial derivatives are approximated by central differential quotients. We inroduce the vetor representing the current flow properties and representing the left hand side of Equations (22) to 24

(26)

in order to apply Jameson’s et al. [9] multi step Runge-Kutta-method accordingly

(27)

(28)

(29)

(30)

(31)

(32)

As mentioned in Section 3 the usage of a central difference approximation for spatial derivatives leads to oscillations which have to be damped. This is done by adding artificial viscosity. The calculation of this numerical viscosity is very time consuming. Thus, we decide to calculate the dissipation terms D only in the first step and leave it constant for the rest of each iteration loop. The integration of the numerical viscosity leads to the following modification of Equations (27)-(32):

(33)

(34)

(35)

(36)

(37)

(38)

The value for in Equations (34)-(38) can not be chosen arbitraryly but has to fulfill the wellknown CFL-criterion [5] . Accordingly, part of our investigations is also the influence of the CFL-number in case of different Mach numbers and ratios of specific heats. We use the formulation, presented by Hirsch in [5] to determine the step-size:

(39)

Figure 3 shows the decrease of the residuum for different and. The local CFL-number is set to 0.6. The shock front remains fixed until an iteration number of 300 is reached. In this region () all graphs are similar. From the iteration number 300 on, the shock fitting method is allowed causing a massive increase of the residuum. This is followed by numerous iterations to adapt the shock front. The iteration number to achieve the final position and shape of the shock front depends on the Mach number and the ratio of the specific heats as Figure 3 shows. It also demonstrates that the reduction of the residuum is faster at higher free stream Mach numbers and lower ratios of specific heats. The massive reduction which is visible at all graphs after a certain number of iterations (e.g. at iteration » 1500 for and) is caused due to the finally positioned shock front. Thus, only small corrections within the flow field are required afterwards. We found out that local CFL numbers with did not lead to convergence for all investigated flow cases because local numerical instabilities caused oscillations which are not damped out sufficiently to decrease the residuum.

To show the grid-independent solution, we selected a high Mach number flow case and. The lift coefficient was chosen to show grid independency. For our calculations only the lower part of the symmetric contour, Equation (39), is considered because this leads to values for and which are not equal to zero. For the flow solver the numbers of grid points on the body surface KX and normal to the wall MX were changed in a way given in Table 1. The results of the grid study can be seen in Figure 4. For the study on Mach number independence, we used 57 × 16 grid points as the deviation of less than »2% to a higher resolution

is sufficient for our purposes.

5. Results

The developed 2D-code was tested on a hyperbolic blunt body contour. The contour has already been investigated earlier by Mundt [14] , and follows the equation

(40)

The contour was analyzed between. The reference point for the pitching moment-the centre of gravity is calculdated to and as the belower half of the body is considered only. The nose radius is 15.49 cm. The analyzed Mach number range is between 3.5 up to 24. The grid consists of 16 × 57 nodes, including boundaries. Results for different aerodynamic coefficients at different free stream Mach numbers and ratios of specific heats are presented in Figure 5.

We did not evaluate the aerodynamic coefficients on the leeward side of the body because the loacal forces are neglible due to the body’s aerodynamic shadow, see [3] . As already said, we only consider the lower part of the contour. As to be expected, with increasing Mach number the aerodynamic coefficients for lift, drag and pitching moment asymptotically approach a certain value, which from a certain Mach number on―only depends on the ratios of the specific heats.

The lift coefficient, see Figure 5(a), decreases with decreasing ratio of specific heats which are not effective isentropic exponents. At the lift coefficient declines continiously from at to at which is a loss of approximately 16%. Regarding the drag coefficient in Figure 5(b) a similar behaviour can be observed. The drop is though lower and leads to. The lift-to-drag ratio, see Figure 5(c), concludes the mentioned facts, resulting in a loss of about 9% from to. The pitching moment coefficient is shown in Figure 5(d). It can be seen that this coefficient is asymptotically tending to 0.098 for all the analyzed ratios of specific heats. One has to realize that the trend of the investigated aerodynamic coeffcients is strongly influenced by the contour and the considered length of the body. Shorter bodies lead to very different values but the mentioned asymptotic behaviour remains. That means in particular that the pitching moment generally varies for different ratios of specific heats and only appears to be independent of the sepcific heats’ ratio for this special contour.

Considering the graphs with in Figure 5(a) to Figure 5(d), the largest gradient is in the region of. For higher Mach numbers the aerodynamic coefficients do not change more than 1.5%. In Figure 6 this gradient is analyzed more in detail. It describes the relative difference to the case for each aerodynamic coefficient. It becomes obvious that the relative difference is larger for lower. The occurance of low ratios of specific heats is typical for high-entalpy flows [7] and reaches its limit with corresponding to the wellknown Newtonian theory. Concluding the findings, Figure 6 indicates that flow field calculations with lower reach their plateau at lower Mach numbers than flows with higher. However, the difference is not very distinctive.

Figure 7 presents shape and location of the shock and the pressue coefficients along the body contour at different free stream Mach numbers and values of. The bow shock stand-off distance reduces with increasing Mach number and decreasing, see Figure 7(a)-(c). Lower ratios of specific heats exhibit higher densities and lead to shock layers that are located closer to the body contour. We are able to derive an approximation for the finally iterated bow shock stand-off distance which provides very good results―error less than 5%―for the investigated body contour with as the noase radius of the body:

(41)

The pressure coefficient in Figure 7 declines continuously from its highest value at the stagnation point at

to its minimum at the outlet boundary Figure 1. The values at the stagnation point are in very good agreement with the Rayleigh Pitot tube formula and changes with different. The lower, the higher the pressure coefficient at the stagnation area. The effect of a loss of pressure is particularly intense at the stagnation point region, yielding to a high pressure gradient along the body surface. The gradient’s amount is essentially higher along the body contour in the case of lower ratios of specific heats. So, we can explain the difference in the values of the aerodynamic coefficients, see Figure 5.

Contour plots of one selected case are shown in Figure 8. The Mach number and the ratio of specific heats are set to and. is Mundt’s body contour [14] , is the calculated shape and position of the bow shock. The initial conditions were set similar to Anderson’s [3] recommendations. One can see that the bow shock lies quite near to the body. This effect is typical for flows at very high Mach numbers and

is besides this amplified by the low ratio of specific heats which leads to a higher density increase. Our solution of Oswatisch’s equations leads to a smooth approximation of pressure contours, see Figure 8(a). Lines of, see Figure 8(c), are due to Crocco’s theorem, Equation (1), identical to streamlines. in this case is the already introduced difference of oblique and normal shock entropy rise, see Equation (17). Thus, it is mandatory that the line lies on the body contour which is also applicable in Figure 8(c). By moving from this contour in body-normal direction a gradient is visible which is caused by the dependency of the entropy in terms of the shock angle, Equation (17). Figure 8(d) describes iso Mach lines. In comparison to flow cases with lower free stream Mach numbers the sonic line turns counterclockwise. Behind the bow shock the Mach number along the body increases continuously and smoothly.

6. Conclusion and Outlook

In this paper, for the first time a technique is introduced solving Oswatitsch’s system of partial differential equations containing the Mach number independence principle succesfully. We present the governing equations, characterize the system and show that a time-dependent solution method is applied in order to take into account the character of subsonic flows at blunt bodies. It is found out that the used Runge-Kutta-algorithm needs to be added by higher values of numerical viscosity in order to achieve convergence in the case of the flow around a hyperbolic blunt body contour with subsonic and supersonic regions. One significant result is that lower ratios of specific heats require a lower Mach number to achieve Mach number independence. From the numerical point of view it is important to mention that the local CFL number has to be lower than 0.7. Further investigations will compare results of Oswatitsch’s equations with results of Euler equations especially in terms of the aerodynamic coefficients. Limitations such as the transfer to chemically reacting flows and the validity on 3D configurations are part of further investigations.

Cite this paper

Volkmar Lorenz,Christian Mundt, (2016) A Method for the Solution of the 2D-Oswatitsch Equations. Journal of Applied Mathematics and Physics,04,844-856. doi: 10.4236/jamp.2016.44092

References

Nomenclature