Journal of Applied Mathematics and Physics
Vol.03 No.12(2015), Article ID:62336,4 pages
10.4236/jamp.2015.312194
Active and Capacitive Conductance of the Diode in a Strong Microwave Field
Muhammadjon Gulomkodirovich Dadamirzaev
Namangan Engineering Pedagogical Institute, Namangan, Uzbekistan

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 October 2015; accepted 26 December 2015; published 29 December 2015
ABSTRACT
It is shown that the mean value of the capacitive current arising in the p-n-junction in a microwave field is zero, and the average value of the active current independently of the current value is different from zero and is equal to the current generated by the diode.
Keywords:
Hot Electrons, The Microwave Field, The Active and Capacitive Conductivity, Fault Current, p-n-Junction

1. Introduction
Under the influence of the electromagnetic wave the average energy of the charge carriers increases in the p-n-junction. As a result, through the potential barrier, current of hot electrons and holes flows. On the other hand, due to changing of the height of the barrier at the contact, alternating current generated by the electric field of the wave will be rectified. Due to the fact that the directions of the currents of hot carriers and rectified currents are the same, so defining the true mechanism of generation of electromotive force (EMF) on diode is an important issue. The interaction of an electromagnetic field with a semiconductor heats the free electrons and holes, and the electrons directly interact with phonons, which lead to heating of the semiconductor [1] [2] .
In [3] [4] the effect of heating of the lattice on the kinetics of the establishment of the thermoelectric power of hot carriers in p-n-junction is theoretically studied. It is shown that the lattice heating leads to an additional third stage of the establishment of the thermoelectric power and thermoelectric hot carriers during the relaxation time determined by the thermal conductivity and heat capacity of the sample [4] . It is also shown that the third stage is slower than the previous two stages, which are established by A. I. Veynger and S. M. Sargsyan [5] .
Effect of warming up of the charge carriers in the operation of semiconductor rectifying structures was first considered by G. M. Avakyantsom [6] . In the future, this task was carried out many studies [1] [7] [8] .
In the p-n-junction with the hot carriers thermoelectric power for the different currents was studied and CVC was theoretically obtained in thin p-n-junction. In the paper of Guliamov G. and Shamirzaev S. H. [9] CVC of p-n-junction was considered, taking into account the heating of the crystal lattice and carriers. Work [10] is devoted to theoretical research of action of effect of Frenkel on the recombination centers p-n-junction, located in a microwave field. Later, the mechanisms of occurrence of EMF and current in the p-n-junction in strong microwave fields were explained in detail [4] [11] . Hitherto in the literature for calculating the current arising in the p-n-junction in the microwave fields the active current is not taken into account relative to the capacitive current, considering it negligible. On the external circuit comes out the average values of these currents. However, the average values of these currents in the literature are not evaluated.
The aim of this work is to study and compare the active and capacitive conductivity arising in the p-n-junc- tion in a strong microwave field.
2. Theoretical Calculations of the Active and Capacitive Conductivity of the Diode in a Strong Microwave Field
To calculate the EMF and currents generated in the p-n junction the differential conductance in the form of active and reactive components Ia and Ir can be written in the following form [12] :
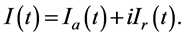 (1)
(1)
Here,
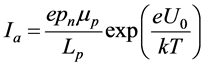 , (2)
, (2)
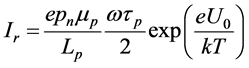 , (3)
, (3)
here, e is the charge of an electron, T is the lattice temperature, k is the Boltzmann constant, pn―concentration and Lp―diffusion length of holes into the n region, tp and mp―respectively the lifetime and mobility of holes, U0―applied voltage, w―cyclic frequency.
Consider the ratio of the second term to the first in Equation (1):
 (4)
(4)
We estimate Equation (4) in the microwave range. For this we use the typical parameters of the samples used in the experiments A. I. Veyngera and others [13] [14] , where ν = 1010 Hz, tp = 10−5 s. Then the ratio of the first term to the second, we have ~3 × 105. This shows that the reactive current by several orders of magnitude higher active current conduction.
Based on these facts we can conclude that in the experiments capacitance diode completely bypasses its active differential resistance Rg. Indeed, at frequencies of the order of ν = 1010 Hz capacitive diode current will be much larger than the active current through the p-n junction. In this case, the active conductivity of the p-n-junc- tion is heavily shunted by the capacitive conduction of the diode and the sample is almost completely loses its rectifying property. In experimental studies [13] [14] based on these considerations, believed that the generated current to the diode in a microwave field only occurs due to heating of charge carriers, and the convection current neglected.
On the other hand the total current density is made up of convection currents and displacement currents:
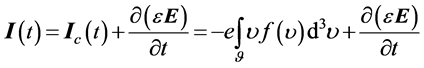 . (5)
. (5)
Here, the first term is an active, and a second capacitive current, Iс(t)―current density of convection associated with the motion of free charges,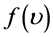 ―the distribution function of the velocity of charge carriers; e― dielectric permeability of crystal lattice, Е―intensity electric field.
―the distribution function of the velocity of charge carriers; e― dielectric permeability of crystal lattice, Е―intensity electric field.
We estimate the current convection and the bias current in the p-n-junction, located in a microwave field. Convection current can be written as:
 . (6)
. (6)
Here U(t)―can be estimated by the formula [15] :
 , (7)
, (7)
where P―Power, ―the differential resistance of the p-n-junction. If we assume that the field of
―the differential resistance of the p-n-junction. If we assume that the field of
the p-n-junction 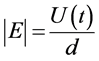 (where d―width of the space charge region of p-n-junction) the formula for the
(where d―width of the space charge region of p-n-junction) the formula for the
total current through the diode can be written as follows:
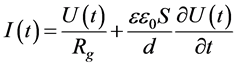 . (8)
. (8)
Here 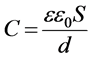 the geometric capacitance of p-n-junction.
the geometric capacitance of p-n-junction.
Leaving the diode current when exposed to microwave field is determined by the average current during the period of the wave. We average the total current in the microwave field:
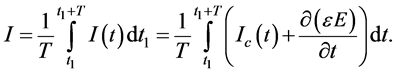 (9)
(9)
We calculate the average value of the bias current:
 (10)
(10)
The electric field is a periodic function of time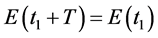 , resulting in the average value of the bias current is always zero. Then the average value of the current generated by the diode is located in a microwave field will be equal to:
, resulting in the average value of the bias current is always zero. Then the average value of the current generated by the diode is located in a microwave field will be equal to:

This current is due to the active current, a capacitive current will not affect the average value of the total current emitted from the diode. This is a simple but important conclusion to explain averaged currents arising on different diodes when exposed to the electromagnetic field. It should be noted that the expression of BAX p-n-junction (11) corresponds to any diode with an asymmetric p-n-junction. For example, contact metal-semi- conductor, Schottky diode, a tunnel diode, metal-insulator-metal and others can relate to these diodes.
3. Conclusion
Based on the analysis of the results obtained it can be concluded that no matter how large the capacitive current is, its average value is zero. Because the electric field is a periodic function of time with period T. No matter how small the active current is, the average value is not zero, and the average current generated by diode is determined precisely by this current. In p-n junction, the active current is closed with the recombination current and total average current is determined by recombination of electrons and holes.
Acknowledgements
The author would like to thank G. Gulyamov, G. Dadamirzayev and N. Yu. Sharibayev for numerous discussions.
Cite this paper
Muhammadjon GulomkodirovichDadamirzaev, (2015) Active and Capacitive Conductance of the Diode in a Strong Microwave Field. Journal of Applied Mathematics and Physics,03,1684-1687. doi: 10.4236/jamp.2015.312194
References
- 1. Buss, A.G. and Gurevich, Y.G. (1975) Hot Electrons, and Strong Electromagnetic Field in the Plasma of Semiconductors and Gas Discharge. Nauka, Moscow, 389 p.
- 2. Bass, F.G., Bochkov, B.S. and Gurevich, Y.G. (1984) The Electrons and Phonons in Bounded Semiconductors. Nauka, Moscow, 288 p.
- 3. Sah, C.T., Noyce, R.H. and Shockly, W. (1957) Carrier Generation and Recombination in p-n-Junctions and p-n-Junctions Characteristics. Proceedings of the IRE, 45, 1228-1243.
http://dx.doi.org/10.1109/JRPROC.1957.278528 - 4. Guliamov, G., Dadamirzaev, M.G. and Boydedaev, S.R. (2000) Kinetics of the Establishment of the Thermoelectric Power of Hot Carriers in the p-n-Junction, Taking into Account Heating. Semiconductors, 34, 266-269.
- 5. Veynger, A.I. and Sargsiyan, M.P. (1980) The Kinetics of the Thermopower Arising in the p-n-Junction with Heating Carrier. Semiconductors, 14, 2020-2027.
- 6. Avakyants, G.M. (1954) On the Theory of Contact Phenomena When. Journal of Experimental and Theoretical Physics, 27, 333-338.
- 7. Veynger, A.I., Paritssky, L.G., Akopyan, E.A. and Dadamirzaev, G. (1975) Thermoelectric Power of Hot Carriers in the p-n-Junction. Semiconductors, 9, 216-224.
- 8. Bonch-Bruyevich, V.L., Zvyagin, I.P. and Mironov, A.F. (1972) Blast Electrical Instability in Semiconductors. Nauka, Moscow, 414 p.
- 9. Gulyamov, G. and Shamirzaev, S.H. (1981) Thermoelectric Power of Hot Carriers in the p-n-Junction, Taking into Account Heating. Lattice Semiconductors, 15, 1858-1861.
- 10. Gulyamov, G., Dadamirzaev, M.G., Boydedaev, S.R. and Gulyamov A.G. (2007) Nonideality Factor of CVC of p-n-Junction in a Strong Microwave Field. International Scientific Conference: Nonequilibrium Processes in Semiconductors and Semiconductor Structures, Tashkent, 1-3 February 2007, 147-148.
- 11. Guliamov, G., Dadamirzaev, M.G. and Boydedaev, S.R. (2000) EMF Hot Carriers Due to the Modulation of the Surface Potential in a Strong Microwave Field. Semiconductors, 34, 572-575.
- 12. Picos, G.E. (1965) Fundamentals of the Theory of Semiconductor Devices. Nauka, Moscow, 448 p.
- 13. Ablyazimova, N.A., Veynger, A.I. and Pitanov, V.S. (1988) The Electrical Properties of Silicon p-n-Junctions in Strong Microwave Fields. Semiconductors, 22, 2001-2007.
- 14. Ablyazimova, N.A., Veynger, A.I. and Pitanov, V.S. (1992) The Impact of a Strong Microwave Field in the Photovoltaic Properties of Silicon p-n-Junctions. Semiconductors, 26, 1041-1047.
- 15. Usanov, D.A., Skripal, A.V. and Ugryumova, N.V. (1998) The Negative Resistance in Structures Based on the p-n-Junction in a Microwave Field. Semiconductors, 32, 1399-1402.
http://dx.doi.org/10.1134/1.1187600

