Journal of Applied Mathematics and Physics
Vol.03 No.11(2015), Article ID:61564,14 pages
10.4236/jamp.2015.311177
Study of the Intrinsic Recombination Velocity at the Junction of Silicon Solar under Frequency Modulation and Irradiation
El Hadji Ndiaye, Gokhan Sahin, Moustapha Dieng, Amary Thiam, Hawa Ly Diallo, Mor Ndiaye, Grégoire Sissoko
Laboratory of Semiconductors and Solar Energy, Physics Department, Faculty of Science and Technology, University Cheikh Anta Diop, Dakar, Senegal

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 30 September 2015; accepted 27 November 2015; published 30 November 2015

ABSTRACT
In this study, a method for determining the intrinsic recombination velocity at the junction of a silicon solar cell is presented. The expression of intrinsic recombination velocity at the junction was established under irradiation in frequency modulation. Based on this expression, an electrical model of the intrinsic recombination velocity at the junction is presented.
Keywords:
Silicon Solar Cell, Frequency Modulation, Intrinsic Recombination Velocity at the Junction, Irradiation Energy

1. Introduction
Photovoltaic conversion is provided by a solar photovoltaic cell whose conversion efficiency depends on the nature and the semiconductor structure, its manufacturing technique and operation. Given the low efficiency of these solar cells, researchers have been involved in various research works by offering several characterization techniques of the semiconductor material and in particular on the design of solar cells. Among the most important parameters in the different techniques characterization, one can cite: the diffusion coefficient  [1] [2] , the global rate of generation of carriers G [3] , the lifetime of the carriers τ, the diffusion length of the carriers L and the intrinsic recombination velocities (Sf at the junction, on the back face Sb) [4] [5] . From theoretical studies, we propose in this paper, a method for determining the intrinsic recombination velocity at the junction of a silicon solar cell monofaciale under monochromatic illumination in frequency dynamic regime under irradiation and finally an electric circuit model equivalent was presented [6] [7] .
[1] [2] , the global rate of generation of carriers G [3] , the lifetime of the carriers τ, the diffusion length of the carriers L and the intrinsic recombination velocities (Sf at the junction, on the back face Sb) [4] [5] . From theoretical studies, we propose in this paper, a method for determining the intrinsic recombination velocity at the junction of a silicon solar cell monofaciale under monochromatic illumination in frequency dynamic regime under irradiation and finally an electric circuit model equivalent was presented [6] [7] .
2. Theoretical Study
The photovoltaic cell considered is of type n+ pp+ [8] [9] and its structure is presented at the Figure 1.
Under the effect of an excitation (optical or electric) of the charge carriers are generated in the base the photovoltaic cell. They can either pass through the space charge region where they participate in the external current, or they undergo recombination. The latter are due to defects (grain boundaries, impurity atoms...) related to the manufacture of the light silicon solar. Taking into account the generation phenomena, diffusion and recombination in the solar cell, the equation of continuity the minority carrier charge in the base at x frequency in dynamicregime is of the form:
 (1)
(1)
where D* is the diffusion coefficient G and the global rate of generation of carriers. The determination of the diffusion coefficient and the global rate of generation proves fundamental for the study of a solar cell in static regime or frequency dynamic regime. Indeed, several studies have been done on the global rate of generation and the diffusion coefficient [10] in order to improve the performance of conversion. Indeed, this last describes the diffusive nature of minority carriers in material, in other words it expresses the capacity of the carriers to be spread within material. Different expressions of the global rate of generation and diffusion coefficient are proposed:
a) Global rate of generation under monochromatic illumination [11] .
The expression of the global rate of generation under monochromatic illumination in frequency dynamic regime and static mode is given by the relation:
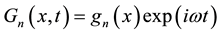 (2)
(2)
with gn(x) the space component and 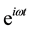 time component.
time component.
According to the illumination mode the generation rate gn(x) as follows:
For illumination of the front face: (n = 1)
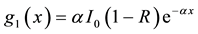 (3)
(3)
For illumination the back face: (n = 2)
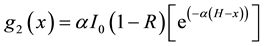 (4)
(4)
For simultaneous illumination of two faces: (n = 3)
 (5)
(5)
a(l) is the absorption coefficient at the wavelength l; I0 is the flux incident monochromatic light; R(l) is the
Figure 1. An n+-p-p+ type of a silicon solar cell under applied magnetic field.
reflection coefficient at the wavelength l; H is the thickness of the solar cell.
b) Global rate of generation under polychromatic illumination [12] .
The expression of the global rate of generation under polychromatic illumination is given by:
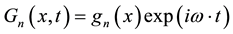 (6)
(6)
According to the illumination mode, the generation rate gn(x) is as follows:
For illumination of the front face:
 (7)
(7)
For illumination the backface:
 (8)
(8)
For a simultaneous illumination of two face:
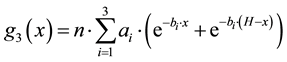 (9)
(9)
ai and bi are coefficients deduced from solar radiation under AM 1,5 spectrum; we set n = 1 (Number of sun).
c) Diffusion coefficient according to the rate of doping [13] .
The doping of semiconductors is an important element for the manufacture of electronic components. Indeed, a pure semiconductor (intrinsic) is almost insulating at the ambient temperature, with a valence band almost entirely full, and a tape of conduction almost entirely empty. Therefore, the interesting electronic properties are related to the possibility “of doping” material by the introduction of adequate impurities making it possible to introduce free carriers. The diffusion coefficient depends on the doping level is given by the equation:
 (10)
(10)
where 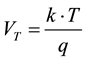 is the thermal tension, K the Boltzmann constant, q elementary charge and Nb is the rate of
is the thermal tension, K the Boltzmann constant, q elementary charge and Nb is the rate of
doping in the base.
d) Diffusion coefficient according to the magnetic field [14] .
The expression of the diffusion coefficient D* as a function of magnetic field in the static mode is given by the relationship:
 (11)
(11)
D0 is diffusion constant without magnetic field, μ is the electron mobility and B is the intensity of the magnetic field.
e) Diffusion coefficient according to the rate of doping and the magnetic field [15] .
The expressions of the coefficient of diffusion and diffusion length according to the magnetic field and rate of doping on a photovoltaic cell with static rate were proposed. It is given by the relation:

L(Nb, B) is the diffusion length of the minority carrier in the base under the influence of the magnetic field and the doping level. It is given by the following expression:
f) Diffusion coefficient according to the frequency [16] .
The expression of the diffusion coefficient as a function of frequency is given by the following relationship:

With D is the coefficient of minority carrier diffusion in the base without of pulsation, radiation and magnetic field.
g) Diffusion coefficient according to the frequency and the rate of doping [17] .
Under the effect of doping rate, the expression of the diffusion coefficient in frequency dynamic regime is of the following form:

h) Diffusion coefficient according to the frequency and the magnetic field [18] .
Frequency in the dynamic regime and under the effect of a magnetic field, the expression of the diffusion coefficient is given by the following relationship:

with 
i) Diffusion coefficient according to the frequency, the damage coefficient and radiation energy [10] .
The terms of the diffusion coefficient and diffusion length depending on the radiation energy and damage coefficient by frequency dynamic regime are given respectively by the following equations:




with


L0 is the diffusion length without of pulsation, radiation and magnetic field.

j) Diffusion coefficient according to the frequency, the damage coefficient, the radiation energy and the magnetic field [20] .
The expression of the diffusion coefficient as a function of the modulation frequency and the intensity of the magnetic field is given by equation

k) Diffusion coefficient according to the recombination velocity at the grain boundaries and grain size [21] .
The diffusion coefficient in function of the recombination velocity at the grain boundaries and the grain size is obtained from the solution of the equation of continuity of the three-dimensional base. By using the boundary conditions, we obtain two transcendental equations. The expressions transcendental equations and the diffusion coefficient are given respectively by the following Equations (21), (22) and (23).



gx is the width of the grain, gy the length of the grain Sgb effective recombination velocity at grain boundaries, Ck and CJ are the eigen values of transcendental equations. From these equations, we will draw the expressions of eigen value CK and CJ based on the recombination rate at the joints and of the grain size. Thus the expression of the diffusion coefficient as a function of the grain size g and the recombination velocity at grain boundaries is given by equation (24):

l) Diffusion coefficient according to the temperature [22] .
The diffusion coefficient based on the static state temperature is given by the relationship Albert Einstein which is written in the form:


m) Diffusion coefficient according to the electric field [24] .
Under the effect of an electric field and static regime the diffusion coefficient of minority carriers in the base is given by the following expression:

where LE is a factor that accounts for the phenomena of migration in the base of the solar cell.
After having pointed out some expressions of global generation and diffusion coefficient, we can solve a priori the continuity equation. For the resolution of the continuity equation, the overall rate of generation and minority carrier’s density can be expressed in the following form, respectively.



Thus Equation (1) can be put in the form:

The Equation (30) being a differential of the second degree with second member thus the general solution is:

For the determination of the coefficients A and B we are used the boundary conditions [25] following.
At the junction (x = 0)

At the back surface (x = H)

where Sf and Sb are respectively the recombination velocity of minority charge carriers at the junction and at the back face; Sf is the sum of two contributions: [26]

Sf0 is the intrinsic recombination velocity at the junction induced by the shunt resistor and the Sfj is the recombination velocity related to the load imposing the point of operation on the photovoltaic cell.
3. Photocurrent Density
The photocurrent is obtained by the gradient of minority carriers at junction and is given by the following expression:

where q is the elementary charge. On Figure 2, we represented the profile of photocurrent density versus the
Figure 2. Photocurrent density module versus recombination velocity Sb. λ = 0.6 µm; ω = 0.6 μm rad/s.
recombination velocity at the back side Sb:
The shape of this curve shows that for the photovoltaic cells of the type BSF (low Sb), the density of photocurrent is maximum for finally decrease until reaching a constant value for the great Sb values modelling solar cells of an ohmic type.
4. Expressions of the Intrinsic Recombination Velocities at the Junction SF0.
The intrinsic recombination velocity at the junction recombinatoires characterizing certain phenomena of excess minority carriers in solar cells surfaces, is investigated to check their qualities. Thus, studies have been conducted on the determination of intrinsic expressions of recombination velocities at the junction into static regimes, transient and frequency dynamic in monochromatic or polychromatic illumination. Indeed, the shape of the curve of variation of the photocurrent density of the modulus versus the recombination rate at the back side Sb shows that at high values of the recombination rate at the back side Sb, these curves show each horizontal level. The gradient of the photocurrent compared to Sb tends then towards zero. Thus, the intrinsic recombination velocity at the junction is obtained by derivation of the density of the photocurrent (Jph) compared to the recombination velocity at the back face Sb.

Depending on the system studied and the manner of illumination of the solar cell, a number of expressions of the intrinsic recombination velocity at the junction Sf0 have been proposed.
a) Static regime [27] [28]
When the bifacial solar cell is illuminated by its front or its rear face with a monochromatic light, the intrinsic recombination velocity at the junction is given by the following expressions.
For illumination of the front face:

For illumination the back face:

For simultaneous illumination of two face:

When the solar cell is under polychromatic illumination via its front or its rear face, expressions intrinsic recombination velocity at the junction are given by:
For illumination of the front face:

For illumination of the back face:

For simultaneous illumination of two face:

Parameter bi is coefficient deduced from solar radiation under AM 1,5 [29] .
In the three-dimensional model, the intrinsic recombination velocity at the junction which takes account of recombination velocity at the grain boundaries is given by:
Under polychromatic illumination:

Under monochromatic illumination:

with

k, j: directions related indexes x and y respectively.
Lkj: Username scattering length associated with modes j and k in the database.
b) Transient dynamic regime [30] .
When the transient dynamic regime is obtained by varying the operating point of a solar cell under constant multispectral illumination, the intrinsic recombination velocity at the junction depends on the eigenvalues of the transcendental equation is given by:

or

The expression of the intrinsic recombination velocity at the junction is:

In the presence of magnetic field, it has the same expression but with D which depends on the magnetic field. We have:

c) Frequency Dynamic regime [31] .
When illuminates the bifacial solar cell with a multispectral light frequency modulation, new expressions of the intrinsic recombination speeds are obtained:
• For illumination from the front side, the intrinsic recombination velocity at the junction is given by:

• For illumination the back face, the intrinsic recombination velocity at the junction is given by:

• If a simultaneous illumination of both sides, the intrinsic recombination velocity at the junction is given by:

In these expressions 

The profile of each intrinsic recombination velocity considered, shows an increase in speed as a function of the modulation frequency of the illumination; with the result that it y' has a very significant recombination of excess minority carriers in the junction of the photovoltaic cell. When one varies the incident wavelength, in addition to the modulation frequency, the same expressions of intrinsic recombination velocities above are obtained. These recombination rates decrease as a function of wavelength.
5. Bode Diagram of the Intrinsic Recombination Velocity
The expression of the intrinsic recombination velocity at the junction of a photovoltaic cell in monofociale frequency dynamic mode under monochromatic illumination in the presence of magnetic field and under irradiation energy is given by the following expression:

The phase of the intrinsic recombination velocity at the junction Sf0 versus the logarithm of frequency for different values of the flow is shown in Figure 3.
It is noted that the quasi-static regime Sf phase is negative, so the capacitive effects predominate, by dynamic system comprises a frequency, the phase Sf is both negative and positive. In this case, simultaneously inductive effects and capacitive effects.
6. Nyquist Diagram of the Intrinsic Recombination Velocity at the Junction and Model Electrical Equivalent
In Figure 4 we represent the Nyquist diagram of the recombination rate at the junction for different values of the irradiation energy.
To better interpret Figure 4, there is shown in Figure 5 the imaginary part as a function of the real part of the intrinsic recombination velocity at the junction to a value of the irradiation energy. Then the imaginary part of the intrinsic recombination velocity at the junction Sf01 is plotted against the logarithm of the modulation frequency in Figure 6.
Graphically, we find that 
It is observed that these curves have an elliptic form with values negative and positive of the imaginary part of Sf0 which justify the capacitive and inductive effects previously cities. One deduces from it that the energy lost by capacitive effect is entirely restored by inductive effect, which justifies the stability of our model.
Nyquist diagram of intrinsic recombination velocity allows us to determine two specific values of this velocity for a value of the irradiation energy. One corresponding to the diameter of the ellipses denoted Sf0,p (for w®¥) and the other denoted Sf0,s (for w®0) (see Figure 5). Thus assimilating the values Sf0,s and Sf0,p of this velocity to the operating points respectively in open circuit of the solar cell and short circuit of the solar cell. We can determine the series resistance Rs (related to Sf0,p) where open circuit of the solar cell and parallel resistance Rp
Figure 3. Phase of Sf versus logarithm of ω for various irradiation energy. B = 10−5 T; Kl = 10 cm2/s; λ = 0.6 µm; φ = 50 MeV.
Figure 4. Imaginary part of Sf versus its real part for various irradiation energy. B = 10−5 T; Kl = 10 cm2/s; λ = 0.6 µm 1: ϕp = 50 Mev; 2: ϕp = 100 Mev; 3: ϕp = 150 Mev; 4: ϕp = 200 Mev; 5: ϕp = 250 Mev.
Figure 5. Imaginary part of Sf versus its real part.
(related to Sf0,p) where short circuit of the solar cell by using calibration curves 

The Figure 7 shows the equivalent electrical circuit of the intrinsic recombination velocity at the junction when using the Nyquist diagram (Figure 4), characterized the capacitive and inductive phenomena observed in the representation of the frequency depending on the phase (Figure 3) where C is the capacitance; L is the inductance and the parallel resistance Rp characterized carriers flight resistance at the base-rear contact interface
Knowing the values of the parallel resistor Rp and cutoff frequency value [34] we can deduce the capacity from the relation ship:

From this Table 1, we find that when the value of the irradiation energy increases, the resistance decreases RP which is due to the slowdown in minority carrier diffusion caused by irradiation. Consequently, the intrinsic properties of the solar cell are damaged; this implies a lower quality of the cells [32] [33] .
Figure 6. Imaginary part of Sf versus the logarithm of ω. B = 10−5 T; Kl = 10 cm2/s; λ = 0.6 µm; φ = 50 Mev; B = 10−5 T; Kl = 10 cm2/s; φ = 50 Mev; λ = 0.6 µm.
Figure 7. Equivalent electric model.
Table 1. Electric and intrinsic parameters of the intrinsic recombination velocity at the junction Sf0.
7. Conclusion
A theoretical study has been performed on the intrinsic recombination velocity at the junction of a Sf0 monofaciale silicon solar cell and under monochromatic illumination modulation frequency and irradiation. This study allowed us to remember the expressions of the global generation rate depending on the type of illumination and expressions of the diffusion coefficient according to some electrical parameters. In addition, the study of the intrinsic recombination velocity at the junction has allowed us to highlight the different relationships of the intrinsic recombination velocity at the junction following the plans and the type of illumination. Indeed, this study also allowed us to show that frequency dynamic regime, the model of the recombination rate at the junction Sf0 is ideal. Moreover with an applied irradiation energy, recombination of the minority carriers is slowed. Taking into account these results, an equivalent electrical model of the intrinsic recombination velocity at the junction has been proposed.
Cite this paper
El HadjiNdiaye,GokhanSahin,MoustaphaDieng,AmaryThiam,Hawa LyDiallo,MorNdiaye,GrégoireSissoko, (2015) Study of the Intrinsic Recombination Velocity at the Junction of Silicon Solar under Frequency Modulation and Irradiation. Journal of Applied Mathematics and Physics,03,1522-1535. doi: 10.4236/jamp.2015.311177
References
- 1. Sontag, D., Hahn, G., Geiger, P., Fath, P. and Bucher, E. (2002) Two-Dimensional Resolution of Minority Carrier Diffusion Constant in Different Silicon Materials. Solar Energy Materials & Solar Cells, 72, 533-539.
http://dx.doi.org/10.1016/S0927-0248(01)00202-1 - 2. Zoungrana, M., Zerbo, I., Sere, A., Zouma, B. and Zougmore, F. (2009) 3D Bifacial Study of Silicon Solar Cell under Intense Light Concentration and under External Magnetic Field Constant. Global Journal of Engineering Research, 10, 113-124.
- 3. Ahmed, F. and Garg, S. (1986) International Centre for Theoretical Physics (ICTP), Internal Report. Trieste, August.
- 4. Ly, I., Lemrabott, O.H., Dieng, B., Gaye, I., Gueye, S., Diouf, M.S. and Sissoko, G. (2012) Recombination Parameter Determination Techniques and Their Field of Validity of a Bifacial Solar Cell Polycrystalline Silicon in Constant Multi Spectral Irradiance under Static Conditions. Renewable Energy Magazine, 15, 187-206.
- 5. Ly Diallo, H., Wade, M., Ly, I., Ndiaye, M., Dieng, B., O. H Lemrabott, A.S. and Maiga Sissoko, G. (2012) 1D Modeling of a Bifacial Solar Cell Silicon under Monochromatic Illumination Frequency Modulation: Determination of the Equivalent Electrical Circuit Related to the Recombination Area Velocity. Research Journal of Applied Sciences, Engineering and Technology, 4, 1672-1676.
- 6. Mbodji, S., Ly, H., Dioum, A., Ly Diallo, H., Barro, F.I. and Sissoko, G. (2006) Equivalent Electric Circuit of Bifacial Solar Cell in a Transient State Under Constant Magnetic Field. Proceedings of the 21st European Photovoltaic Solar Energy Conference and Exhibition, Dresden, 447-450.
- 7. Diallo, M.M., Seibou, B., Yoro BA, H., Zerbo, I. and Sissoko, G. (2014) One-Dimensional Study of a Bifacial Silicon Solar Cell Illuminated from the Front area by a Monochromatic Light Frequency Modulation under Influence of Irradiation Damage and Coefficient. Current Trends in Technology and Science, 3, 416-421.
- 8. Chenvidhya, D., Kirtikara, K. and Jivacate, C. (2005) PV Module Dynamic Impedance and Its Voltage and Frequency Dependencies. Solar Energy Materials and Solar Cells, 86, 243-251.
http://dx.doi.org/10.1016/j.solmat.2004.07.005 - 9. Hübner, A., Aberle, A.G. and Hezel, R. (2001) 20% Efficient Silicon Solar Cells Bifacial. 14th European PVSEC, Munich, 1796-1798.
- 10. Tall, I., Seibou, B., El Moujtaba, M.A.O., Diao, A., Wade, M. and Sissoko, G. (2015) Diffusion Coefficient Modeling of a Silicon Solar Cell under Irradiation Effect in Frequency: Electric Equivalent Circuit. International Journal of Engineering and Technology Trends (IJETT), 19, 56-61.
- 11. Dugas, J. (1994) 3D Modelling of a Reverse Cell Made with Improved Multicrystalline Silicon Wafers. Solar Energy Materials and Solar Cells, 32, 71-88.
http://dx.doi.org/10.1016/0927-0248(94)90257-7 - 12. Misiakos, K., Wang, C.H., Neugroschel, A. and Lindholm, F.A. (1990) Simultaneous Extraction of Minority-Carrier Parameters in Crystalline Semiconductors by Lateral Photocurrent. Journal of Applied Physics, 67, 321-333.
http://dx.doi.org/10.1063/1.345256 - 13. Xing, Y., Han, P., Wang, S., Liang, P., Lou, S., Zhang, Y., Hu, S., Zhu, H., Mi, Y. and Zhao, C. (2013) Analysis of Effects of Front and Back Surface of One Vertical Silicon Dopants Multi-Junction Solar Cell by 2D Numerical Simulation. Science China Technological Sciences, 56, 2798-2807.
http://dx.doi.org/10.1007/s11431-013-5378-z - 14. Ngom, M.I., Zouma, B., Zoungrana, M., Thiam, M., Bako, Z.N., Camara, A.G. and Sissoko, G. (2012) Theoretical Study of a Multi-Junction Silicon Cell under Multispectral Parallel Vertical Illumi Nation: The Influence of External Magnetic Field on the Electrical Parameters. International Journal of Advanced Technology & Engineering Research (IJATER), 2, 101-109.
- 15. Liu, J.J. and Wong, W.W. (1992) Comparison and Optimization of the Performance of Si and GaAs Solar Cells. Solar Energy Materials and Solar Cells, 28, 9-28.
http://dx.doi.org/10.1016/0927-0248(92)90104-W - 16. Ndiaye, M., Nouhou Bako, Z., Zerbo, I., Dieng, A., Barro, F.I. and Sissoko, G. (2008) Determination of Electrical Parameters of a Solar Cell under Monochromatic Illumination on FM, from Diagrams Bode and Nyquist. Journal des Sciences, 8, 59-69.
- 17. Zerbo, I., Kooalaga, Z., Barro, F.I., Zougmore, F., Ndiaye, A.L., Diao, A. and Sissoko, G. (2004) Silicon Solar Cell Parameters Determination under Recombination Frequency Modulated White Light Using the Short Loop Current Phase. Journal des Sciences, 4, 42-46.
- 18. Diao, A., Thiam, N., Zoungrana, M., Sahin, G., Ndiaye, M. and Sissoko, G. (2014) Diffusion Coefficient in Silicon Solar Cell with Applied Magnetic Field and under Frequency: Electric Equivalent Circuits. World Journal of Condensed Matter Physics, 4, 84-92.
http://dx.doi.org/10.4236/wjcmp.2014.42013 - 19. Ly Diallo, H., Dieng, B., Ly, I., Dione, M.M., Ndiaye, M., Lemrabott, O.H., Bako, Z.N., Wereme, A. and Sissoko, G. (2012) Determination of the Recombination and Electrical Parameters of a Vertical Multijunction Silicon Solar Cell. Research Journal of Applied Sciences, Engineering and Technology, 4, 2626-2631.
- 20. Mbaye, M.F., Zoungrana, M., Thiam, N., Diao, A., Sahin, G., Ndiaye, M., Dieng, M. and Sissoko, G. (2013) Study of the Photo Thermal Response of a Solar Cell in Mono Facial Dynamic Diet under a Multispectral Illumination and under Magnetic Field. International Journal of Engineering and Science Inventive, 1, 60-66.
- 21. Deme, M.M., Mbodj, S., Ndoye, S., Thiam, A., Dieng, A. and Sissoko, G. (2010) Influence of Illumination Angle Grain Boundary Recombination Size and Grain Velocity on the Facial Solar Cell Diffusion Capacitance. Review of Renewable Energy, 13, 109-121.
- 22. Dieme, N., Seibou, B., Moujtaba El, M.A.O., Gaye, I. and Sissoko, G. (2015) Thermal Behavior of a Parallel Vertical Junction in Silicon Photocell Diet by Static Study of the Series and Shunt Resistors under the Effect of Temperature. International Journal of Innovative Science, Engineering & Technology, 2, 433-437.
- 23. Kunst, M. and Sanders, A. (1992) Transport of Excess Carriers in Silicon Wafers. Semiconductor Science and Technology, 7, 51-59.
http://dx.doi.org/10.1088/0268-1242/7/1/009 - 24. Zerbo, I., Zoungrana, M., Seré, A.D., Ouedraogo, F., Sam, R., Zouma, B. and Zougmoré, F. (2011) Influence of an Electromagnetic Wave on a Silicon Solar Cell in Multi Spectral Irradiance Regime in Statique. Revue of Renewable Energy, 14, 517-532.
- 25. Sissoko, G., Museruka, C., Correa, A., Gaye, I. and Ndiaye, A.L. (1996) Spectral Light Effect on Recombination Parameters of Silicon Solar Cell. Proceedings of World Renewable Energy Congress, Part 3, Denver, 15-21 June 1996, 1487-1490.
- 26. Sissoko, G., Correa, A., Nanema, E., Diarra, M.N., Ndiaye, A.L. and Adj, M. (1998) Recombination Parameters Measurement in Sijicon Double Sided Surface Field Cell. Proceedings of the World Renewable Energy Conference, Florence, 20-25 September 1998, 1856-1859.
- 27. Barro, F.I., Zerbo, I., Lemrabott, O.H., Zougomore, F. and Sissoko, G. (2001) Bulk and Surface Recombination Measurement in Silicon Double Sided Surface Field Solar Cell under Constant White Bias Illumination. Proceedings of 17th European Photovoltaic Solar Energy Conference and Exhibition, Munich, 22-26 October 2001, 368-371.
- 28. Dione, M.M., Ly, I., Diao, A., Gueye, S., Gueye, A., Thiame, M. and Sissoko, G. (2013) Determination of the Impact of the Grain Size and the Recombination Velocity at Grain Boundary on the Values of the Electrical Parameters of a Bifacial Polycristallin Silicon Solar Cell. IRACST—Engineering Science and Technology: An International Journal (ESTIJ), 3, 66-73.
- 29. Noor Mohammad, S. (1987) An Alternative Method for the Performance Analysis of Silicon Solar Cells. Journal of Applied Physics, 61, 767-772.
http://dx.doi.org/10.1063/1.338230 - 30. Thiam, N., Diao, A., Ndiaye, M., Dieng, A., Thiam, A., Sarr, M., Maiga, A.S. and Sissoko, G. (2012) Electric Equivalent Models of Intrinsic Recombination Velocities of a Bifacial Silicon Solar Cell under Frequency Modulation and Magnetic Field Effect. Research Journal of Applied Sciences, Engineering and Technology, 4, 4646-4655.
- 31. Zerbo, I., Barro, I.F., Mbow, B., Diao, A., Zougmore, F. and Sissoko, G. (2004) Theoretical Study of Bifacial Silicon Solar Cell under Frequency Modulated White Light: Determination of Recombination Parameters. 19th European Photovoltaic Solar Energy Conference, Paris, 7-11 June 2004, 258-261.
- 32. Mora-Sero, I., Garcia-Belmonte, G., Boix, P.P., Vazquez, M.A. and Bisquert, J. (2009) Impedance Spectroscopy Characterization of Highly Efficient Silicon Solar Cells under Different Illumination Intensities Light. Energy and Environmental Science, 2, 678-686.
http://dx.doi.org/10.1039/b812468j - 33. Suresh, S. (1996) Measurement of Solar Cell Parameters Using Impedance Spectroscopy. Solar Energy Materials and Solar Cells, 43, 21-28.
http://dx.doi.org/10.1016/0927-0248(95)00153-0 - 34. Dieng, A., Zerbo, I., Wade, M., Maiga, A.S. and Sissoko, G. (2011) Three-Dimensional Study of a Polycrystalline Silicon Solar Cell: The Effect of the Magnetic Field on the Applied Electrical Parameters. Semiconductor Science and Technology, 26, Article ID: 095023.
http://dx.doi.org/10.1088/0268-1242/26/9/095023










