ABSTRACT

Chern-Simon theory and the holographic principle as well as scale relativity are used to find out the exact value of cosmic ordinary and dark energy density. The result agrees completely with previously obtained ones as well as with accurate cosmic measurements.

Keywords:Holographic Boundary, Chern-Simon Theory, Dark Energy, Cosmic Expansion, Fractal-Cantorian Spacetime

1. Introduction and Background Information

We start the present analysis of determining the dark energy density of the cosmos [1] -[12] in a reverse order to the heading of the paper at hand by recalling an important result of Nottale’s scale relativity [11] , namely that the inverse coupling of GUT tends to a “highly particular” value 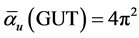as the energy tends to infinity [13] . This is stated explicitly in his well-known book [13] on page 264. In other words the relevant running of U(1), SU(2) and SU(3) does not intersect in the conventional way but rather tends asymptotically towards an imaginary intersection point at infinity. This is of course a consequence of the fractal nature of Nottale’s theory and in that respect quite satisfying and logically appealing as far as our Cantorian view point is concerned [4] - [13] . However we showed on an earlier occasion [14] [15] that continuity introduces spurious terms to the relevant equations and transfiniteness require higher order correction terms [15] similar in spirit to radiation corRections albeit in this case Cantorian-fractal corrections leading to 4 → 4 + f³ and p² → 10 where

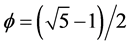[16] . The exact transfinite inverse coupling in this case is thus not 4p² = 39.47 but rather (4 +

f³)(10) = 42 + 2k = 42.36067977 [17] . The interesting point in this slight discrepancy of the magnitude of 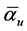comes to the fore when we consider the automorphism of the classical 336 degrees of freedom Klein modular curve, then we have 336/2 = 168 such automorphism [18] . Again looking at a relevant cycle of this curve which plays the role of a holographic boundary to a bulk given by E8E8 exceptional Lie symmetry group, then we arrive at what we may call field strength of the magnitude F = 168/2 = 84 [19] . This gives us our first result of interest, namely that

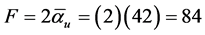. (1)

The exact transfinitely corrected expression is of course [16]

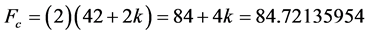(2)

where 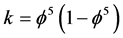and. On the other hand field strength F corresponds to the curvature in the Chern-Simon theory of fiber bundles [20] and is given by F = 8p². In other words it harmonizes with scale relativity when written in the form

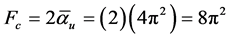. (3)

In the next section of the present work we will examine the preceding result in some detail [20] -[44] .

2. Field Strength and Dark Energy

Our present thesis however is that 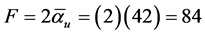is the correct expression and that it leads us in this way to a correct appreciation of the exact value and the role of the holographic degrees of freedom in determining the ratio between the directly accessible to the indirectly accessible energy stored in our fiber bundle-like universe and in fact a superstring conception of our cosmos [9] -[12] [21] -[25] . Our point is that F = 84 minus 10 give us the dark energy component of the total energy density as expressed by the sum of all the fundamental inverse couplings [16] [21] .

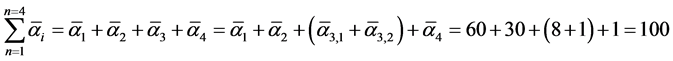. (4)

That means

(5)

In other words 74 percent of the total energy is pure dark energy not counting dark matter. Our sum may therefore be rewritten as

(6)

where the ordinary energy component is given by (ordinary) = 4 and the dark matter component is given by (dark matter) = 22. Needless to say, the preceding analysis and conclusions need further elaboration for a proper understanding of the deep message we are trying to convey. To start with the normed hundred percent sum of all the fundamental inverse coupling needs refinement and elucidation. The, 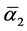and 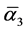are idealized theoretical values which happen to be related to the electroweak scale. They are very close indeed to the experimental values found in numerous experiments [26] [27] to be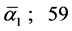, , 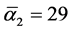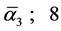[29] [30] . On the other hand 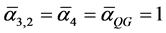are related to the quantum gravity Planck scale [26] -[29] . Never the less all the four inverse couplings enter into a special form of an exact renormalization equation from which the fundamental electromagnetic inverse constant may be reconstructed as [29] [30]

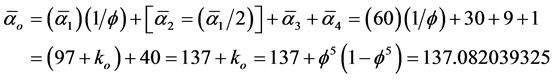. (7)

For the above reasons we regard the sum of being 100 as a weighted number of the involved space and internal dimensions just as could be regarded as a cross-section or a quantum probability for a photon to capture or emit an electron while at the same time 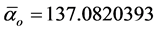may be regarded as a dimension of a fractal space in which the electron “moves” [16] [30] . Thus 100 is a weighted total dimension comparable with the 496 of E8E8 or the 528 of the manifold of killings vector fields associated with Witten’s 5D Branes in eleven dimensions [31]

. (8)

In this sense the subdivision of the sum of has to be undertaken more delicately to reveal its hidden inner fine structure. To start with the 22 of the sum 22 + 4 + 74 must be 22 + k = 22.18033989 to bring it in harmony with the Hardy’s quantum entanglement and the previous result of ordinary energy

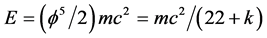. Similarly the 4 must become the ordinary energy percentage which is

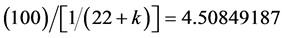. Consequently the pure dark energy exact percentage must be

.

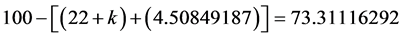3. Dark Energy from the Holographic Boundary

Now we can return to the holographic theory and how to calculate the ordinary energy component directly and subsequently the dark energy and dark matter components indirectly [4] -[12] [32] -[35] . For clarity we start with the integer approximate form of the theory. We know that the holographic boundary has no gravity degrees of freedom since gravity resides inside the Bulk. Thus the only degrees of freedom are those given by

which is in a one to one correspondence with the degrees of freedom of Klein’s modular curve as indicated earlier on. Einstein’s gravity on the other hand has in D = 4 twenty independent Riemannian components corresponding to 20 degrees of freedom in super symmetric D = 8 space for pure gravity. From these twenty, four dimensions were already used in Einstein’s spacetime so that we are left with effectively only 20 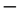4 = 16 degrees of freedom. Our reduced Lorentzian factor is now clearly equal to the ratio of these 16 to the 336 holographic degrees of freedom after amplification by adding the 20 of the Riemann-Einstein independent “degrees of freedom” and subtracting the D⁽⁴⁾ = 4. That way we find

(9)

exactly as anticipated [32] -[35] . The dark energy density is consequently the maximal energy density E = mc² minus the ordinary energy density E(0) = mc²/22 which means [35] -[38]

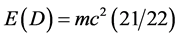. (10)

For the sake of completeness we give without much elaboration two exact transfinite formulas for E(0) and E(D) which effectively boils down to using the transfinitely compactified holographic boundary 336 → 336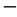

16k where 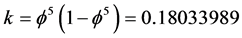and is Hardy’s probability of quantum entanglement [36] . Proceeding in this way one finds that

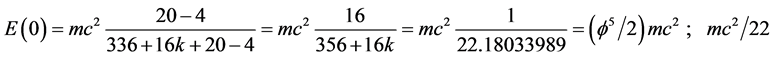(11)

and

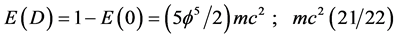. (12)

Again this is in full agreement with previous analysis [4] -[12] [32] -[38] and accurate cosmological measurements [1] -[3] .

4. Conclusion

The present analysis of the dark and ordinary energy density in the cosmos centres is around three main ideas, namely scale relativity, Chern-Simon theory and the holographic principle. The so obtained results, i.e. E(0) = mc²/22 and 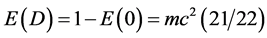agree completely with all previous analysis [4] -[12] [32] -[35] as well as cosmic measurements [1] -[3] . Wider aspects of the present theory which go beyond mainstream physics and cosmology are discussed in reference [39] as well as [40] and [41] where the question of infinitely many dimensions is considered. In addition we recently made considerable advances in using the physical concepts of fluid mechanics and nonlocal elasticity to understand the nature of dark energy [41] [42] . Finally it is important to mention a major finding regarding ‘t Hooft’s dimensional regularization and a corresponding fractal Cantorian spacetime leading to a dark energy density equal to that found using accurate cosmic measurements [43] [44] .

References