ABSTRACT

This article studies the ratio of the rates of profit and growth, in a growing economy, as a function of the average productivity of capital. It is shown that, if the savings rate and also the distribution of income between wage and profit are constant, the ratio mentioned remains constant or increases if the average productivity of capital respectively does not change or changes at a steady rate, whether it increases or decreases. If the change is repeated throughout a sufficiently large number of production cycles, the first rate grows above the second, even if in the initial situation the second rate is higher than the first. The result is the same if the savings rate and the rate of change of the average productivity of capital fluctuate within certain limits over a sufficiently large number of production cycles. In each case, the number of cycles required depends on the initial situation and the magnitude of the changes in both variables. These conclusions are compatible with the relevant historical data for economic variables involved. For this reason, they help to explain why, as a general rule, in a modern economy the rate of profit is higher than the growth rate.

Keywords:

Average Productivity of Capital, Growth and Profit Rates, Income Inequality, Piketty, Sraffa

1. Introduction

Piketty ( [1] , pp. 350-358) shows that, as a general rule, in a modern economy the profit rate is higher than the growth rate and that, when this is not the case for a country during a given period, it is nevertheless possible that the capital owned by some persons in that country obtain a profit rate greater than the country’s growth rate. The greater the gap of the first over the second rate, the greater the volume of capital disposable for a capital owner for further investment above that required to keep constant his fraction of the country’s capital stock. The investments, either partial or complete, of the extra amounts of earned capital enlarge the corresponding personal fractions. This enlargement is more likely to benefit the largest fractions, as individuals with greater capital endowments tend to obtain higher profit rates (Piketty [1] , pp. 430-467). In turn, this result together with the fact also shown by Piketty ( [1] , pp. 271-303) that, contrarily to what happens in other income strata, personal incomes consisting mainly of profits are predominant among the highest strata, produces a tendency for income to concentrate in the hands of those occupying these strata. To underline the importance of this effect, Piketty ( [1] , pp. 25-27) distinguishes the inequality between the two rates as the main cause of the increase of income inequality. In regard to the origin of the first inequality, Piketty ( [1] , p. 358) says that it is a historical fact that derives from multiple causes and, in a later work, Piketty ( [2] , p. 49) notes that this inequality holds true in the steady state equilibrium of the most common economic models. It should be added that the book cited has been debated in a large number of publications (e.g., Aspromourgos [3] , Galbraith [4] , Grantham [5] , Lindert [6] , Mankiew [7] , Rognlie [8] , Solow [9] ).

This article complements the works just mentioned by studying the ratio between the rates of profit and growth in a growing economy as a function of the average productivity of capital (APK), a topic not previously treated in the specialized literature, as far as I know. To isolate this relation from the effects of changes in the distribution of income over the two rates, I consider a succession of production cycles where such distribution is the same in all cycles. The main result states that if the saving rate is constant, the ratio of the rates of profit and growth remains constant or increases if the APK respectively does not change or changes at a steady rate, whether it increases or decreases. The increase in the ratio is due to that, by increasing or reducing the APK, both profit and growth rate respectively increase or decrease but, in the first case, the profit rate increases in a greater proportion and, in the second one, decreases in a smaller proportion than the growth rate. If the change is repeated throughout a sufficiently large number of production cycles, the first rate grows above the second, even if in the initial situation the second rate is higher than the first. The result is the same if the savings rate and the rate of change of the APK fluctuate within certain limits over a sufficiently large number of production cycles. In each case, the number of cycles required depends on the initial situation and the magnitude of the changes in both variables. By means of examples, it is shown that the conclusions reached are compatible with the relevant historical data for economic variables involved. For this reason, they help to explain why, as a general rule, in a modern economy the rate of profit is higher than the growth rate. However, to know to what extent these conclusions allow to explain the difference between the two rates in particular economies and historical periods, it is necessary to perform econometric studies for each case.

In addition to this introduction, the text contains four sections and one Appendix. Section 2 presents the basic model of Sraffa [10] and the growth path studied here. Section 3 defines the relevant variables for the study and also exposes some of its properties. Section 4 explores the relations between profit and growth rates. Section 5 summarizes the main results and the Appendix presents the proofs of some mathematical propositions.

2. The Growth Model

In this Section, I present the basic model of Sraffa and the growth path studied here.

2.1. Sraffa’s Basic Model

I consider a succession of production processes starting at dates 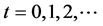and, to identify each one of them, I refer to the date corresponding to the end of production. There are 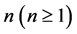industries each one producing a particular type of good. To each good, and to the industry producing that good, corresponds an index i or j so that 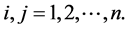For each pair 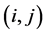and for each j, 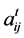and 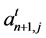are respectively the quantities of i and of labor consumed directly in the production of one unit of j in period t. 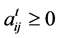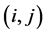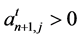I assume that for every and for every j. For each t, the 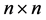matrix 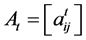represents the means of production technical coefficients and its Frobenius root is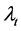. Every good is basic which means that each good produces every good either directly or indirectly. This implies that 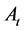is indecomposable and, for this reason,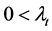. Furthermore, I assume that 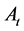is viable (see Benítez [11] ), which means that:

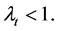(1)

For each couple 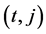and for each t, 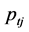and vector are respectively the price of good j and the price system of produced goods in period t. The wage is paid at the end of production and the profit rate is the same in all industries. In these conditions, the relation between the price and the cost of production of each good allows to formulate the following equation system:

(2)

Making, system (2) determines prices measured in wage units that correspond to each level of the rate of profit within an interval described in Section 3.2. Multiplying those prices by the wage measured with any given bundle of goods result prices measured in that bundle.

It should be added that one of the constraints of the model presented here, the fact that includes only those goods that produce all the goods, may be overcome using the Leontief’s closed model once the adaptations required are introduced. Indeed, as Benítez [12] shows, that model allows representing an economy in which not all goods are basic using a model in which all are.

2.2. The Growth Path

For each couple, the quantity of good j produced in period t is and vector indicates the goods produced in the period. Due to the fact that matrix is indecomposable, the equation system:

(3)

has a unique solution determined up to a scalar factor. This equation implies that, for each good, the ratio between the quantity used as input and the amount produced is equal to.

For, the magnitude of vector is fixed by the equation:

(4)

while, for, that magnitude is fixed by the equation:

(5)

where, for each, is the growth rate of the economy from period to period t, which is determined as indicated in Section 3.4. It is worth noting that the vector of quantities produced in each production cycle is a multiple of the vector that corresponds to each of the other cycles.

Let and, for each, let:

(6)

These definitions together with Equation (5) allow writing, for each:

(7)

For each, the production program of period t is obtained by multiplying each equation of system (2) by the corresponding coordinate, resulting:

(8)

In each period t, the transactions take place at two different calendar dates. Those corresponding to the beginning of the production process are made in the afternoon of day t−1 and those corresponding to its end are made in the morning of day t.

3. Average Productivity of Capital, Profit and Growth Rates

In this Section, I present the definitions and some properties of the main variables considered in this study.

3.1. Capital and National Income

It follows from Equation (3) that, for every t, it is possible to represent the set of goods used in production and the set of goods that constitute the net product respectively by vectors and. Thus, the capital and the national income of period t are determined by:

(9)

and

(10)

Then, the capital/income ratio of period is given by:

(11)

Þ

(12)

Therefore, this ratio is independent of the distribution of income and depends only on the technique of the period considered.

For the purposes of this paper it is not necessary to choose a particular unit for measuring prices. However, it is worth mentioning that adopting for this task the whole product of the first period of production permits to relate some of the macroeconomic variables just defined with the growth rates of the different production periods. Indeed, for every, if prices are measured in period t with the whole product of the first period, then:

(13)

On the other hand, multiplying both sides of Equation (7) by yields:

(14)

Equations (13) and (14) imply that:

(15)

This result and the definitions of capital and national income presented above imply respectively that:

(16)

and

(17)

Due to the fact that these formulas are independent of changes in relative prices taking place in the different production periods, they facilitate comparing capital and income pertaining to those periods.

3.2. Profit Rate

For each t, is the fraction of national income corresponding to wages in period t. I assume that the national income is divided between wages and profits for which the amounts in question are respectively equal to and. Therefore, the profit rate is determined by the equation:

(18)

Þ

(19)

When the profit rate is zero, increases monotonously as decreases and reaches its maximum level when, which is determined by the following equation:

(20)

Equations (19) and (20) imply that:

(21)

According to this equation, the profit rate is equal to the maximum profit rate multiplied by the fraction of national income which corresponds to profits. It should be added that, for each there is a uniquely determined satisfying system (2). Similarly, for every there is a uniquely determined satisfying system (2) (see Benítez [13] ).

Equations (12) and (20) imply that:

(22)

3.3. Capital Growth Rate

For every, is the fraction of national income saved at date t. I asume that:

(23)

I also adopt the following proposition:

Hypothesis 1. In each date t, the set of households consume the goods defined by vector.

As a result, for every, at the end of period t, it is possible to start a new production period investing the goods in vector in addition to the goods invested at the beginning of the period. I assume that this investment takes place whereby, for each, the investment grows from period to period t in a balanced way to the rate determined by:

(24)

(25)

I will refer to as the growth rate of capital. On the other hand, Equation (20) for period is:

(26)

Equations (25) and (26) imply that:

(27)

which means that, from the second period, the growth rate of capital is equal to the product of the maximum profit rate and the fraction of national income devoted to saving which correspond to the preceding period. Since the last two variables are not necessarily the same in all periods, the growth rate of capital can vary from one period to another.

Furthermore, Equation (21) for period is:

(28)

Equations (27) and (28) allow drawing the following conclusion:

Proposition 1. Given two successive production periods, the profit rate of the first period is greater than, equal to, or less than the capital growth rate of the second if in the first period the fraction of national income which corresponds to profit is respectively, greater than, equal to, or less than the fraction of national income destined to savings.

It is important to add that, for each, the vectors of quantities produced in two successive production cycles must satisfy the equation:

(29)

In the next section, I adopt a hypothesis about the technology employed that guaranties the satisfaction of this condition.

3.4. Average Productivity of Capital and Economic Growth Rate

For each, the APK of period t is given by:

(30)

Þ

(31)

It should be noted that, adding one unit on each side of Equation (20) yields:

(32)

(33)

Equations (31) and (33) imply that:

(34)

As a result, the APK and the maximum profit rate both increase or diminish in the same extent and in the same sense although these variations do not represent the same percentage for the two variables. Furthermore, substituting in the right-hand side of Equation (34) by its equivalence according to (22) gives:

(35)

(36)

On the other hand, I assume that, for every, the means of production technical coefficients of two successive periods are related in the following form:

(37)

where is a scalar such that, and is a number defined ahead, in Section 4.2. As no similar assumption is adopted concerning labor coefficients, they may evolve differently than the means of production coefficients. The preceding equation implies that:

(38)

Substituting in Equation (3) by the right-hand side of this equation gives:

(39)

Þ

(40)

According to (iv) from Theorem 4.B.1 by Takayama ( [14] , p. 372) this equation implies that

(41)

Þ

(42)

Equation (41) also implies that:

(43)

Substituting the term between brackets in the left-hand side and also the right-hand side in this equation by their respective equivalences in accordance with Equation (31) yields:

(44)

which means that is the rate of variation of the APK from period to period t. I will also refer to as the growth rate of the APK understanding that it may be negative. In accordance with the preceding equation, given two dates and t such that we have the following set of equations:

(45)

(46)

(47)

(48)

Substituting in the penultimate equation by the left-hand side of the last equation, then substituting in the equation preceding the penultimate equation by the left-hand side of the equation resulting from the first replacement and so on, gives:

(49)

On the other hand, substituting in Equation (29) by the left-hand side of Equation (41) yields:

(50)

Þ

(51)

Therefore, the rate of output growth, or growth rate of the economy from period to period t, is determined by the following equation:

(52)

Þ

(53)

Þ

(54)

The preceding analyses allow drawing the following conclusion.

Proposition 2. The economic growth rate is equal to the sum plus the product of the growth rates of capital and of the APK.

3.5. Average Productivity of Capital and Profit Rate

Substituting in Equation (20) by the right-hand side of Equation (42) results in:

(55)

Multiplying both numerator and denominator of the right-hand side of this equation by yields:

(56)

(57)

On the other hand, Equation (20) which corresponds to the period is:

(58)

Þ

(59)

Þ

(60)

Replacing the first term and the term between brackets of the second term on the right-hand side of Equation (57) respectively by the left-hand side of Equations (58) and (60) yields:

(61)

Multiplying and dividing the right-hand side of this equation by gives:

(62)

Now, substituting in Equation (21) by the right-hand side of this equation results in:

(63)

Since, by hypothesis, it is possible to write Equation (28) in the following form:

(64)

Replacing the first factor between brackets on the right-hand side of Equation (63) by the left-hand side of this equation result in:

(65)

Therefore, it is possible to formulate the following conclusion.

Proposition 3. If the distribution of income between wage and profit in two successive periods of production is the same, the profit rate decreases, remains constant or increases in the second period with respect to the first if the APK of the second is, respectively, less than, equal to, or greater than the APK of the first. In the first and in the third case, the absolute value of the rate at which the rate of profit varies is greater than the one corresponding to the rate of variation of the APK and the difference between these two figures will be lower the greater the maximum profit rate previously to the change of productivity.

4. The Relation between Profit and Growth Rates

In this section, I study different aspects of the ratio between the rates of profit and growth as a function of the APK. In the first subsection, I establish for the factor which, multiplied by the ratio corresponding to production period, gives the ratio corresponding to period t. In the two following subsections I study, under two restrictive assumptions, respectively this factor and its implications on the inequality between the two rates. In the last subsection, I relax the two assumptions.

4.1. The Ratio between Profit and Growth Rates

Equation (62) implies that:

(66)

Now, substituting the sum between brackets in the right-hand side of Equation (65) by the left-hand side of Equation (66) result in:

(67)

On the other hand,

(68)

Dividing Equation (67) term to term by the last equation yields:

(69)

Hence, the ratio of the rates of profit and growth in period t is greater than, equal to, or less than in period if the ratio between the maximum rates of profit of the two periods are respectively, greater than, equal to, or less than the ratio between the corresponding growth rates of those periods. For this reason, I will then study the second factor on the right-hand side of Equation (69).

Equation (66) implies that:

(70)

Furthermore, Equation (61) for the period is:

(71)

Substituting in the right-hand side of Equation (70) the rate by the right-hand side of this equation gives:

(72)

Doing the same substitution in Equation (27) results in:

(73)

Now substituting on the right-hand side of Equation (53) by the right-hand side of this equation gives:

(74)

Similarly, Equation (27) for the period is:

(75)

while Equation (53) for the same period is:

(76)

Substituting in this equation by the right-hand side of Equation (75) results in:

(77)

Equations (72), (74) and (77) allow writing the following conclusion:

(78)

The right-hand side of this equation is the factor which, multiplied by the ratio of the rates of profit and growth of a production period, gives the ratio corresponding to period t. In this formulation, the factor is expressed as a function of the growth rates of the APK in the two periods, the maximum profit rate from period (see Equation (34) for the relation of this rate with the) and the savings rates of periods and.

Furthermore, for each, let:

(79)

Therefore, is the rate at which the ratio of the profit and growth rates varies from period to period t. In what follows, I will represent the right-hand side of Equation (78) indistinctly by the left-hand side of the equation or by the sum.

4.2. The Ratio between the Profit and Growth Rates under Two Restrictive Assumptions

In this Section and in the next one, I assume the following propositions.

Hypothesis 2. In each production period, the same fraction of national income is saved.

Hypothesis 3. In each production period, the APK varies at the same rate.

Let and. Introducing in Equation (78) the substitutions corresponding to the assumptions just adopted and also, to simplify, substituting by R, results in:

(80)

Regarding the magnitude of h in this equation, it is important to note that there is no upper limit for its positive values. However, negative values are limited in accordance with the following proposition.

Lemma 1. For each, there is a minimum level such that, for every, the economy grows, investments respect the criterion of maximizing profit and the division by zero is avoided in Equation (80).

Proof. See Appendix A.2.

For each, h_t,min indicates a range of possible values of h determined by the given values of s and R. Thus, it usually changes from one period to another. The following proposition relates changes in the APK and the sum.

Theorem 1. The sum is equal to one if, and is greater than one for all h different from zero and greater than h_t,min.

Proof. See Appendix A.3.

The preceding analyses allow the drawing of the following conclusions.

Proposition 4. Given two successive production periods in a growing economy in which the distribution of income between wage and profit, the rate of savings and the rate of variation of the APK are constant, the ratio of the rates of profit and growth of the second period is equal to or greater than the ratio of the first period if the rate of variation of the APK is respectively equal to or different from zero but greater than h_t,min.

As can be noted in Equations (65) and (53) when the APK increases or decreases both the profit and the growth rate respectively increase or decrease. This observation and Proposition 4 imply that, in the first case, the profit rate increases in a greater proportion and, in the second one, decreases in a smaller proportion than the growth rate.

In the examples, I use certain data and formulas for the sole purpose of indicating the order of magnitude of a particular variable, as in the case presented below related to the sum. The reproduction through an econometric model of the referred empirical phenomena requires more sophisticated procedures. On the other hand, in the calculations are used only six decimals.

Example 1. According to Figure 3.6 by Piketty ( [1] , p. 128) and Table S1.2 by Piketty [15] private capital measured by national income in France was equal to 6.99 in 1910, from that year decreased coming to 2.19 in 1950 and, starting from this year increased coming to 5.75 en 2010. Thus, substituting in Equation (36) by its corresponding

values yields, and. It follows from

Equation (49) that, if the annual rate of change of the APK had been steady between the first two dates and also between the last two, then and

. Therefore, in the first case, which implies that whereas in the second case

, which implies that. Now, using Equation (22) yields, , and

. For each period, I take as the value of R the average of the

maximum profit rates corresponding to the beginning and the end of the period, then, for the first period and, for the second one,. On the other hand, according to Table FR.3c from Piketty and Zucman [16] , the average annual rate of savings for both periods 1913-49 and 1949-2009 was 12%, I assume that this was the rate corresponding to periods 1910-1950 and 1950-2010. Making substitutions corresponding to the data of the period 1910-1950 in the right-hand side of Equation (80) gives:

(81)

(82)

Hence,

(83)

(84)

Equation (83) shows that both maximum profit and growth rates increased from period to period t, but the first one increased at a greater rate than the second. Because is constant, the profit rate increased in the same proportion as the maximum rate of profit (see Equations (62) and (65)). For this reason, the ratio of the profit and growth rates increased. The average annual rate of increase of the ratio is 0.3342%.

Proceeding in analog form with data from the period 1950-2010 results in:

(85)

Hence,

(86)

(87)

The penultimate equation shows that both maximum profit and growth rates decreased from period to period t, but the first one decreased at a smaller rate than the second. Because is constant, the profit rate decreased in the same proportion as the maximum rate of profit (see Equations (62) and (65)). For this reason, the ratio of the profit and growth rates increased. The average annual rate of increase of the ratio was 0.1478%.

4.3. The Inequality r > g

It follows from Equations (69) and (79) that, given two dates and such that, we have the following set of equations:

(88)

(89)

(90)

(91)

Substituting in the penultimate equation the quotient by the right-hand side of the last equation, then substituting in the antepenultimate equation by the right-hand side of the equation resulting of the first replacement and so on, results in:

(92)

Þ

(93)

Therefore, in order to satisfy the inequality:

(94)

It is enough that:

(95)

(96)

Regarding the magnitude of, it follows from Theorem 1 that, for each, if and, then. In addition, it is useful to consider the following proposition.

Lemma 2. When and R tends to infinity, tends to zero.

Proof. See Appendix A.4.

It follows from this lemma that, in some cases, inequality (96) may not be true for any t or be true only for a t extremely high if R, the quotient or both variables are

big enough. However, the data offered by Piketty indicate historical levels of the variables involved much lower than those required in those two cases, as shown below.

Example 2. Substituting in Equation (92) the data from Example 1, results in:

(97)

(98)

(99)

(100)

Substituting in the right-hand side of Equation (98) the factor within brackets by the right-hand side of Equation (100) gives:

(101)

(102)

Therefore, under the assumptions adopted, the ratio of the rate of profit and the rate of growth in the French economy increased 28.4823% during the period 1910-2010 due to variations of the APK.

4.4. Relaxing Hypothesis 2 and 3

It can be noted in Equation (78) that the quotient is a monotonous increasing function of. Due to this fact, the following proposition is true.

Theorem 2. The sum is a monotonous decreasing function of.

Therefore, provided that the saving rate decreases with respect to its value in the previous period, the sum increases. In the oposite case this quotient decreases and, if the increase in the savings rate is large enough, it can be less than one, as shown below.

Example 3. In the case of period 1910-1950 discussed in Example 1, it follows from Equations (78), (81) and (83) that, for the sum to be less than one, must satisfy the following inequality:

(103)

Þ

(104)

Þ

(105)

Hence, must grow at a rate greater than. That is,

for the ratio of the profit and growth rates to decrease, it is enough that the savings rate increases at a rate greater than 0.3891% from one period to the next. In this regard, it should be noted that the historical series on the value of the savings rate present significant differences in the magnitude of this variable in different countries and also between different historical periods in the same country. However, in the last 70 years, for the USA, Germany, Japan, France, United Kingdom, Italy, Canada, and Australia the savings rate fluctuates in each country around the corresponding national average value, with increases and decreases of the order of one percentage point from one year to the next one (see Piketty and Zucman [16] , respectively Table US.3c, Table DE.3d, Table JP.3b, Table FR.3b, Table UK.12.b, Table IT.3b, Table CA.3b., Table AU.3b).

For a, let the values of, , and the corresponding value of be given. For each, under the assumption that, I define as follows: if for a value of belonging to the interval let be that value, otherwise,. Furthermore, let. Thus, if the rate of change in the APK is constant and greater than in periods and t, the sum is greater than one for every.

Theorem 3. The sum is a monotonous decreasing function of.

Proof. See Appendix A.5.

Therefore, the sum increases when the rate of variation of the APK decreases with respect to its value in the previous period. In the opposite case this sum decreases and, if the increase in the rate of growth of the APK is large enough, it can be less than one, as shown below.

Example 4. In the case of period 1910-1950 discussed in Example 1, it follows from Equations (78) and (81) that, for the sum to be less than one, the variable must satisfy the following inequality:

(106)

Þ

(107)

Þ

(108)

Þ

(109)

Þ

(110)

Þ

(111)

Therefore, must grow at a rate greater than.

That is, for the ratio of the profit and growth rates to decrease, it is enough that the rate of variation of the APK grow more than 2.7109% compared to its value in the previous production cycle.

For any, let the values of, , and be given. Assuming that and also that, let be the greatest value of for which, and let. The preceding analyses allow the following conclusion.

Proposition 5. In a growing economy in which, for each, , , and, the ratio of the rates of profit and growth increases with each production cycle.

It may be noted in Equation (78) that, in the particular case when the savings rate is constant and, we have if. This result together with Theorem 3 and the definition of imply that. Therefore, if the savings rate is constant and in a production period the APK does not change with respect to its value in the preceding period, any increase in the APK in period t produces a diminishing in the ratio of the profit and growth rates.

If the rate of change of the APK is constant, either to increase or to decrease, over a certain number of production cycles, at the end of these cycles result an increase in the ratio of the profit and growth rates and, respectively, an increase or a decrease in the APK of the last cycle with respect to the first. It is important to note that, in accordance with Proposition 4, it is possible to obtain the same variation in the ratio of the profit and growth rates through a succession of production cycles in which the APK at the first and the last cycle are equal. For this purpose it is enough that, throughout all cycles, the APK fluctuates properly, for example initially increasing and then decreasing, respecting the condition stated in Proposition 5, as shown below.

Example 5. Suppose that the APK from the French economy continues to decline, after 2010, at the same annual average rate of the period 1950-2010. In accordance with Equation (49) and with the data from Example 1, the number of years required (x) from 1950 so the APK descends to its level of 1910 must satisfy the equation

. Substituting in this equation the values corresponding to the APK gives. Solving, results, so that

. Thus, because the distribution of income between wage and profit is, by hypothesis, the same on the two dates, is also the same the profit rate. Since the ratio between profit and growth rates increased (see Example 3), the increase is due to the decrease in the rate of growth.

According to these analyses, if between two successive periods of production increases do not occur in the savings rate of the economy nor in the rate of growth of the APK which exceed certain percentages, the ratio between profit and growth rates increases. In a succession of production cycles, even if the percentages indicated are surpassed and this ratio decreases in some cycles, it is possible that these decreases are offset by what happens in other cycles, so that the average of the variations of the proportion that we are interested in is greater than zero.

5. Conclusion

In a growing economy in which remain constant the savings rate and also the distribution of income between profits and wages, when the APK varies at a steady rate, either to increase or to decrease, in each production cycle the profit rate increases with respect to the growth rate. This is due to that, by increasing or reducing the APK, both profit and growth rate respectively increase or decrease but, in the first case, the profit rate increases in a greater proportion and, in the second one, decreases in a smaller proportion than the growth rate. If such variation is repeated throughout a sufficiently large number of cycles, the accumulation of increases leads the first rate to grow above the second, even if in the initial situation the second rate is higher than the first. The same result is reached if the savings rate and the rate of change of the APK fluctuate within certain limits over a sufficiently large number of production cycles; however, if any of these variables increases surpassing the corresponding limit from one period to another, the profit rate may decrease with respect to the growth rate. In addition, the variation in the distribution of income between wage and profit affects the rate of profit and, by consequence, the ratio between the latter and the growth rate of the economy. For these reasons, to know to what extent the fluctuations of the APK explain the relationship between the rates indicated in a growing economy, it is necessary to study individual cases.

Acknowledgements

I am grateful to an anonymous referee for helpful comments and suggestions.

Cite this paper

Benítez Sánchez, A. (2016) Piketty’s r > g Explained by Changes in the Average Productivity of Capital. Theo- retical Economics Letters, 6, 1034-1059. http://dx.doi.org/10.4236/tel.2016.65102

References

Appendix

In the first part of this appendix I present a formulation of Equation (80) that facilitates the demonstrations of the two sections following.

A.1 A Reformulation of Equation (80)

Dividing by s all terms of the denominator of the right-hand side of Equation (80) and making operations there described, it is possible to write the equation in the following form:

(112)

(113)

(114)

(115)

Let:

(116)

(117)

Using this notation, it is possible to write Formula (115) in the following manner:

(118)

Finally, simplifying results in:

(119)

A.2 Proof of Lemma 1

In order to avoid division by zero in Equation (80), and for the economy to grow, respectively, the following three inequalities and the last two of them must be satisfied:

(120)

(121)

(122)

When, the three inequalities are satisfied while, when the left-hand side of each inequality is equal to −1. Also, the three inequalities are continuous functions of h defined on the interval while the first and the third inequalities are monotonous increasing functions of h. Therefore, there is a number for which the left-hand side of the first inequality is equal to zero while, for every it is greater than zero and for every it is smaller than zero. Similarly, there is a number for which the left-hand side of the third inequality is equal to zero while, for every it is greater than zero and for every it is smaller than zero. Moreover, there is at least one number belonging to the interval such that the left-hand side of the second inequality is equal to zero. Let be the maximum value within that range for which this takes place. Thus, the second inequality is satisfied for every while this is not the case for any interval in which.

On the other hand, at the beginning of each production period, in order to maximize profit, it is necessary that the profit expected with additional investment and the new profit rate be greater than or equal to that obtained in the period, since, otherwise, it would be more convenient to repeat the production process of the previous period. As a result, it is necessary that:

(123)

Þ

(124)

Substituting in this inequality by the right-hand side of Equation (65), gives:

(125)

Þ

(126)

Substituting in this inequality by the right-hand side of Equation (73) and also substituting the sum within brackets by the right-hand side of Equation (72) (see Equation (66)), and after adapting the notation, results in:

(127)

When, the right-hand side of this inequality is equal to and, when it is equal to. It should be noted that this side of the inequality is a continuous function of h defined for all. If for some this function is equal to one, let be the maximum value within that range for which this takes place. If not, let. Thus, the inequality is satisfied for every while this is not the case for any interval in which.

The lemma is satisfied making:

(128)

Remark. To demonstrate Theorem 1, it is useful to check separately that division by zero is avoided in Equation(119). For which the following inequalities must be satisfied:

(129)

(130)

(131)

When the three inequalities are satisfied while, when the left-hand side of the first two inequalities is less than zero and the left-hand side of the last one is equal to one. Since the left-hand side of each of the first two inequalities is a monotonous increasing continuous function of h defined on the interval, it follows that there is a number such that, for all the first two inequalities are satisfied while this is not the case for any interval in which. As a result, the left-hand side of inequality (131) is a function of h defined on the interval. Moreover, it is a continuous function of h over this interval. If, for some, the left-hand side of inequality (131) is equal to zero, let be the maximum value within that range for which this takes place, if not, let. Thus, this inequality is satisfied for every while this is not the case for any inter-

val in which. Making in Equation (128), the lem-

ma is satisfied.

A.3 Proof of Theorem 1

As can be noted in Equation (119), if the quotient at the right-hand side is equal to one. Moreover, condition (23) and Equation (117) imply that:

(132)

Therefore, given that, if then:

(133)

Þ

(134)

As a result, the right-hand side of Equation (119) is greater than one. Finally, according to Lemma 1, if, then. This inequality and the following equation:

(135)

allows to conclude that:

(136)

Furthermore, multiplying by h both sides of inequality (132) yields:

(137)

For this reason,

(138)

This result and inequality (130) imply that:

(139)

In turn, this result and inequality (136) imply that:

(140)

Therefore, also in this case inequality (134) is satisfied which, together with inequality (131), imply that the right-hand side of the Equation (119) is greater than one.

A.4 Proof of Lemma 2

Dividing by R each term on the right-hand side of Equation (80), gives:

(141)

Making:

(142)

it is possible to write:

(143)

Hence,

(144)

(145)

(146)

The lemma is inferred from this result and Equation (79).

A.5 Proof of Theorem 3

I will show that the derivative with respect to of the sum is less than zero. Dividing the two bottom lines of equation (78) by results in:

(147)

Let and. Making appropriate substitutions on the right-hand side of the above equation gives:

(148)

(149)

(150)

Deriving with respect to yields:

(151)

Since the sign of the derivative depends only on the sign of the numerator of the above ratio, in what follows I will deal exclusively with this numerator. Multiplying it by B results in:

(152)

Multiplying this result by A gives:

(153)

= (154)

(155)

(156)

(157)

(158)

(159)

(160)

(161)

Condition (23) implies that, this result and the fact that imply that the derivative is negative, ending the proof.