Received 30 April 2016; accepted 6 June 2016; published 9 June 2016

ABSTRACT

This study investigates the oil and stock prices nexus in the US economy over the period 1980- 2016. Using breakpoint regression technique, our findings are twofold: 1) we confirm the existence of the nexus as established in the existing literature on the subject; 2) while the relationship between the oil and stock prices remains intact, the slope changes over time, thus identifying a non-linear relationship.

Keywords:

Oil Prices, Structural Break, US Economy, Slope Heterogeneity

1. Introduction

Stock markets, in any economy, play a vital role not only of providing liquidity services to the stakeholders, but also of helping the corporations to have their own estimates of how much they could raise from the market in form of equity. However, the role of secondary market is not limited to this extent. Where the performance of a particular stock reflects the expected future growth of the company, the overall performance of a stock market reveals the future expected course of economic activity in a country. This makes the stock prices a reliable leading indicator of economic growth worldwide. However, at the same time the stock prices-stock returns as percentage growth in prices also respond to different changes in the economy, where the commodity prices can be listed quite high.

In this regard, though fluctuations in the oil price are often considered important for understanding changes in stock prices, there is no consensus about the relation between stock prices and the price of oil among economists. Some studies claim a negative link between oil and stock price variations, while others observe a positive relationship. Also there is a third strand finding no nexus at all. For instance, Jones and Kaul [1] recorded a negative relationship between oil price and aggregate stock price changes. Kling [2] stated that crude oil price increases were associated with stock market declines. Huang et al. [3] , however, in contrast, found no negative relationship between stock returns and changes in the price of oil futures. Chen et al. [4] suggested that oil price changes had no effect on asset prices. This presents an interesting puzzle in the oil price and stock returns changes.

We revisit this question to find out the missing part of the puzzle. A look into the existing literature reveals some limitations. One issue is that existing work treats the other factors affecting the stock and oil prices as constant and without considering the question of cause and effect. This issue has been addressed by the studies afterwards (Kilian [5] - [7] ), however, the puzzle remains as it was.

Another limitation of the existing literature is that the studies attempt to assess the impact of higher crude oil prices on stock prices without knowing the original causes of the oil price increase. Although in this context the demand and supply shocks in the crude oil market have been studied by Kilian [6] , it still ignores the fact that the external and the structural shocks can also affect the nature of this relationship. Doing so, we believe that such regressions relating stock returns to changes in oil price will give biased results or unstable significant statistical relationships (Sadorsky [8] ).

A third issue with the existing literature is that it mainly focuses on the rising oil price and its impact on the stock returns, while the last decade has remained a roller coaster for oil price. Ignoring the impact of recession and the global economic activity, while considering the oil price and stock returns relationship being linear, is therefore one of the main reasons behind the existing puzzle.

In this article, we attempt to solve the puzzle and analyze the slope of oil price and stock returns relationship, by investigating the breaks in the data, if any. We adopt the methodology of breakpoint regression analysis to analyze the nature of this relationship after and before the structural break(s). In the next Section, we describe the data and the methodology adopted thereafter; in Section 3 we discuss the empirical findings and the Section 4 concludes.

2. Data Description and Pre-Estimation Tests

2.1. Data Description

We use monthly prices of Brent and West-Texas Intermediate (WTI), and selected U.S. stock market variables¹. The sample period is 1980.1-2016.1. The aggregate U.S. real stock return is constructed by subtracting the consumer price index (CPI) inflation rate from the log returns on the S & P 500 and Dow-Jones 30. All the data comes from the DataStream.

It is now customary to evaluate such causal relationships using the vector restricted or unrestricted autoregressive models. The mainstream studies on this subject use from simple ordinary least square (OLS) to structural VAR methods to determine the oil price and stock returns relationship. Whereas a simple OLS regression could also give a quick hunch regarding the status of this relationship in a bi- or multivariate environment, the linearity assumption in this case could give misleading results. The scope of this study is not to reinvent the wheel, but to figure out the main factor causing important differences in the results of various studies. In this context as our baseline hypothesis is that analyzing data containing structural breaks will lead to biased results and can result into a puzzle. To avoid this issue, this study uses the breakpoint regression analysis. We adopt the methodology defined by Bai and Perron ( [9] [10] ).

Consider the following framework:

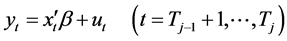(1)

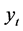Here. In this model, is the observed dependent variable at time t; both are vector of covariate and 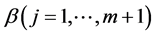is the corresponding vector of coefficients; is the disturbance at time . The indices 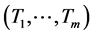or the break points, are explicitly treated as unknown (the convention that

and is used). The purpose is to estimate the unknown regression coefficients together with the break points when T observations on (and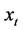) are available².

This is our simple baseline breakpoint regression model. However, before running the regression it is pertinant to study the time series properties of our data. The essential test in this regard is to ensure that the data is stationarity.

2.2. Unit Root Analyses

This is now established that most of the macroeconomic time series contain a unit root (Nelson and Plosser [11] ). The presence or absence of unit roots which is another term to define the non-stationarity or stationarity characteristic of data helps to identify some features of the underlying data generating process of a series. A stationary series fluctuates around a constant long-run mean and indicates that the series has a time independent and finite variance. On the other hand, if the data have a unit root, then it has no tendency to return to its long-run deterministic path and the variance of the series is time dependent. Non-stationary series follow a random walk and suffer from permanent random shocks.

If the series is non-stationary at level, but on the first difference, then it is integrated of order one (1). There is now rich literature on the methods testing for stationarity or otherwise. The commonly used methods in this regard are mainly the Augmented Dickey-Fuller (ADF) tests (Dickey and Fuller, [12] [13] ), Im, Pesaran and Shin [14] test, PP-Fisher test and Levin, Lin and Chu [15] test. While the literature concentrates on whether time series are affected by transitory or permanent shocks, this can be tested by the ADF model, which is primarily concerned with the estimate of α.

Testing the null hypothesis of 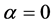against the alternative hypothesis of:

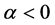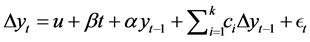(2)

where ∆ denotes the first difference, y is the variable in question, t is the trend, and k is the number of lags which are added to the model to ensure that the residuals, has a constant variance that is uncorrelated with for. The optimal lag length or k is determined by using Schwarz Bayesian Criterion (SBC) (Schwarz [16] ) and Akaike Information Criterion (AIC) (Akaike [17] ), with a null hypothesis of the series having a unit root. Conducting different stationarity tests we establish that both the oil prices and stock prices series are non-stationary at level (see Table 1).

We find that our variables are stationary at first difference. However, as the basic objective of this study is to determine if the data contains any breaks, a breakpoint unit root test would be more appropriate. As the past decade recorded significant ups and downs in the oil price and the stock returns as well, one can link the stationarity of the data to the stationarity of changes over the period in question.

2.3. Unit Root Tests in the Presence of Structural Break

This is understood that economic data series contain structural breaks particularly the historical data sets. In this case a simple unit root test may give misleading results. Perron [18] argues that in the presence of a structural break, the standard ADF tests could be biased towards the null hypothesis. He adds that though most macroeconomic series are not characterized by a unit root, the tenacity comes only from large and sporadic shocks, and that the fluctuations are indeed stationary around a deterministic trend function.

Notes: 1. ^**for Fisher tests are computed using an asymptotic Chi-square distribution. All other tests assume asymptotic normality. 2. The Levin, Lin and Chu test assumes common unit root process as the null hypothesis. Im, Pesaran and Shin, ADF and PP tests assume individual unit root process as the null hypothesis. 3. Exogenous variables: Individual effects. 4. Newey-West automatic bandwidth selection and Bartlett kernel.

Perron [18] modifies Dickey-Fuller (DF) unit root tests by including dummy variables to account for one known, or exogenous structural break, thus its procedure is characterized by a single exogenous break in accordance with the underlying asymptotic distribution theory. Perron’s [18] unit root test allows for a break under both the null and alternative hypothesis. Although these tests have less power than the standard DF test without a break, Perron [19] points out that they are consistent whether there is a break or not and have a correct asymptotic size.

Here we adopt the same procedure as that of Glynn et al. [20] based on Perron [18] . Accordingly the three equations take into account the existence of three kinds of structural breaks: one that allows for a break in the level of series; another that allows break in slope and the third one that allows both effects to occur simultaneously.

(3)

(4)

(5)

where the is the intercept dummy representing a change in the level; if and zero otherwise-TB is the break date; the (also) is the slope dummy and represents a change in the slope of the trend function; (or if) and zero otherwise; the dummy if, and zero otherwise. Each of the three models has a unit root with a break under the null hypothesis, as the dummy variables are incorporated in the regression under the null. The alternative hypothesis is a broken trend stationary process.

Table 2 describes the unit root tests with breaks. These results support our baseline hypothesis of the presence of structural break in the data and allows for a breakpoint regression analysis³.

3. Empirical Findings

As mentioned above, studies in general consider the oil price and stock returns relationship being linear and ignore the slope heterogeneity of the relationship between oil price and stock returns. This can result into biased findings and this is one reason we find no consensus on the nature of oil price and stock returns relationship. In this article, we attempt to fill in these gaps, however, by not introducing additional variables, but our main focus

Notes: 1. Perron and Vogelsang [21] asymptotic one-sided p-values; 2. Break selection: minimize DF t-statistic (Break Data: 2009M01); 3. Lag Length: based on Schwarz information criterion; 4. ^***, ^** and ^* indicate 10%, 5% and 1% of significance, respectively.

remains on the slope of the nexus. In this regard, the breakpoint regression is a suitable and simple way to study such relationship. Therefore, to identify the breaks in the data we use Bai-Perron [10] method of sequentially determined breaks. This test is widely used in literature to check for breakpoints and one of the advantages of this test is that it can capture more than one breakpoint in the data.

The result confirms the existence of breakpoint in the data and supports the selection of breakpoint unit root tests. The test defines September 2008 as the breakpoint in our data (Table 3). This allows us to use the breakpoint regression as a next step.

Our regression results though confirm the existing claims of the literature in this regard, one can see in Table 4, a very interesting result that answers the puzzle as described earlier. Whereas, some studies find a negative while the others a positive relation between oil prices and stock returns, our results justify the accuracy of both strands of literature. We find that the slope of oil prices and stock return nexus is not linear and over the time the slope changed significantly. A detailed look into the studies focusing on a negative relationship between oil prices and stock returns reveal that they only used the data roughly till the break point. On the contrary the studies establishing a positive relationship have used the data after the breakpoint. In this context we can also understand the reasons behind the inconclusive results of a third strand of literature on the subject. If used a longer data series without taking care of the breaks in the data, the results could be misleading or inconclusive.

Notes: 1. ^*Significant at the 5% level. 2. Bai and Perron [10] critical values.

Notes: 1. Break type: Bai-Perron tests of L + 1 vs. L sequentially determined breaks. 2. Break selection: Trimming 0.15; max. breaks: 5; sig. level: 0.05; break: 2008M09.

4. Conclusions

Literature is rich on the subject of oil prices and stock prices nexus, however, the existing studies reveal some gaps. Firstly, while some researchers link oil price changes to stock returns in a multivariate framework controlling for many factors (Wei [22] ). In other words, they treat oil prices as strictly exogenous with respect to the global economy, which is not very credible (Barsky and Kilian [23] [24] ; Hamilton [25] ). This is now established that global macroeconomic fluctuations have influenced the price of crude oil since the 1970s (Kilian [5] ). So not just the supply but the demand side has played a vital role in the oil prices and in turn the stock returns as well.

Second, existing models postulate that the effect of an exogenous increase of decrease in the price of oil is the same, regardless of the causal shock driving up the price of oil. Kilian [7] has shown that the effects of demand and supply shocks in the crude oil market on US macroeconomic aggregates are qualitatively and quantitatively different, depending on the cause of the shock in question. This fact was well captured by Kilian and Park [26] , and they came up with the suggestion of relaxing the existing ceteris paribus assumption in studying the relationship between oil prices and stock returns. However, these studies in general consider this relationship being linear and thus ignore the slope heterogeneity of the relationship between oil price and stock returns.

In this study we apply a different method to study the link between the oil price and stock returns for the US economy. The existing studies on the subject suffer from different weaknesses. Most of the studies consider the oil prices as exogenous and ignore the global demand and supply factors that could cause different consequences of any oil price change. In this context the studies also ignore of importance of slope analyses of this relationship and usually consider it as a linear one.

This study attempted to explore these weaknesses. Our baseline hypothesis was to study the slope of the oil price and stock returns relationship. Applying any method to such data series will not give the actual results unless we take care of the breaks in the data. This study, therefore, goes a step further and investigates the statistical reasons behind the existing puzzle in the oil prices and stock returns nexus.

The empirical findings are twofold: a) this study confirms the existence of a relationship between oil prices and stock returns as established in the literature; b) the study finds a breakpoint in the data during September 2008, on the basis of which it was observed that the relationship between oil prices and stock returns changed significantly. We see a negative relationship between our two variables before the breakpoint, while the relationship becomes positive afterwards. This result implies that though oil price have a significant impact on the economic activity, the nature of this impact can change depending on the overall macroeconomic conditions of the economy. In this regard, the impact of the great recession could be on the back of the break as found in the data. However, this claim needs to be strengthened by further evidence.

Cite this paper

Sarfaraz Ali Shah Syed,Hélène Syed Zwick, (2016) Oil Price Shocks and the Us Stock Market: Slope Heterogeneity Analysis. Theoretical Economics Letters,06,480-487. doi: 10.4236/tel.2016.63055

References

Appendix

NOTES

¹We use the S & P 500 and Dow-Jones 30 indices being the most widely used data in the literature.

²To keep the space used limited, we are not repeating the details of the model; however these could be obtained from Bai and Perron [9] [10] .

³A visual presentation is also available in Figure A1 and Figure A2 in Appendix.